Ne vom ocupa de expresiile aritmetice în care intervin operatorii binari , , , si cuprinderea între paranteze. Vom considera ca expresiile cu care lucram sunt corecte.
Pentru simplificare, vom presupune ca variabilele care apar în expresii sunt litere.
Scopul propus consta în evaluarea expresiilor (presupunând ca variabilele au valori stabilite 737b13h oarecare) si în generarea codului corespunzator expresiei, într-un limbaj de asamblare ad-hoc.
stim ca:
o expresie este o "suma" de termeni (între care intervin numai operatorii de adunare si scadere);
un termen este un "produs" de factori (între care intervin numai operatorii de înmultire si împartire);
un factor este fie o variabila, fie o expresie între paranteze.
Gramatica independenta de context corespunzatoare, cu simbolul initial E, este:
E T+E | T-E | T
X l
T T*F | T/F | F
F litera | (E)
Primul pas în rezolvarea problemelor enuntate consta în constructia arborelui binar atasat expresiei.
Exemplu. Expresiei aritmetice ((a-b)*(a+c))/(d-(e+f)) îi corespunde arborele:
unde etichetele vârfurilor sunt et=(/,*,-,-,+,d,+,a,b,a,c,e,f)
Vom prezenta un program Java care construieste direct acest arbore; la intrare poate sa apara orice exprsie aritmetica (cu conditia sa fie corecta) urmata de un caracter ce nu apartine gramaticii.
Generarea codului pentru expresii aritmetice
Presupunem ca nu avem restrictii de memorie (deci putem introduce oricâte variabile suplimentare) si ca dispunem de un registru r pentru efectuarea operatiilor. Instructiunile disponibile si semnificatiile lor sunt urmatoarele:
LOAD x r ← x
STORE x r → x
x r ← r x, unde
Observam ca toate instructiunile au doua câmpuri.
Se considera ca toate aceste instructiuni necesita acelasi timp de executare.
Nu vom lua în considerare nici una dintre proprietatile algebrice ale operatiilor (comutativitate, asociativitate, distributivitate), nici posibilitatea reducerilor unor termeni si nici eventuala aparitie a unor subexpresii care se repeta.
Dorim sa construi un un cod (o succesiune de instructiuni de tipurile de mai sus), a carui executare sa aduca în registrul r valoarea expresiei aritmetice. Dorim de asemenea ca acest cod sa fie optim adica sa fie format dintr-un numar minim de instructiuni.
Observatie În orice cod neredundant:
numarul de instructiuni de tipul 3) este egal cu numarul vârfurilor interne, deci cu numarul operatorilor ce apar în expresie; prin urmare acest numar este fix;
orice instructiune LOAD, afara de prima, este precedata imediat de o instructiune STORE. Codul începe cu o instructiune LOAD.
Cu alte cuvinte, numarul instructiunilor LOAD este mai mare cu o unitate decât cel al instructiunilor STORE: LOAD)=#(STORE)+1. De aceea un cod optim este un cod cu un numar minim de instructiuni STORE .
Este evident ca pentru construirea codului, arborele trebuie parcurs în postordine.
Atasam fiecarui vârf x codul Cx în care în prima instructiune lipseste câmpul LOAD
Vârfurilor terminale (frunzelor) x le atasam codul: _ et(x)
Pentru vârfurile neterminale x vom folosi codurile atasate subarborelui stâng st si subarborelui drept dr. Deosebim urmatoarele cazuri:
daca descendentul drept al lui x este o frunza, codul Cx va fi:
Cst
et(x) Cdr
daca descendentul drept al lui x nu este o frunza, se observa ca este mai convenabil (din punctul de vedere al numarului de instructiuni) sa începem cu evaluarea subarborelui drept:
Cdr
STORE T
LOAD Cst
et(x) T
unde T este o variabila suplimentara.
Variabilele suplimentare vor fi notate cu Tk, unde k este initial si creste cu o unitate la fiecare constructie a unui nou cod pentru un vârf al carui descendent drept nu este o frunza.
Pentru exemplul considerat mai sus obtinem succesiv:
C a
C b
C a
- b
C a
C c
C a
+ c
C a
+ c
STORE T1
LOAD a
- b
* T1
C d
C e
C f
C e
+ f
C e
+ f
STORE T2
LOAD d
- T2
C e
+ f
STORE T2
LOAD d
- T2
STORE T3
LOAD a
STORE T1
LOAD a
- b
* T1
/ T3
Programul în Java
Constructia arborelui urmeaza întocmai definitia expresiilor aritmetice: va fi scrisa câte o metoda pentru expresie, termen si factor.
Fiecare vârf (obiect de tipul clasei varf) are câmpurile st dr si et desemnând respectiv descendentul stâng, cel drept si eticheta sa.
Se presupune ca variabilele sunt litere mici de la începutul alfabetului.
Mai este folosita o variabila ch care joaca rolul unui "spion" catre caracterul urmator din expresie.
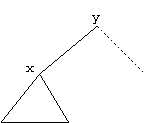Vom folosi asociativitatea la stânga a operatorilor.
De exemplu daca un termen începe cu un "produs" de factori
pentru care am construit arborele de radacina x si urmeaza un factor pentru care am
construit obiectul y x va deveni descendent stâng al lui y, care va fi radacina noului arbore
corespunzator termenului:
import java.util.*;
class Expresie
class varf
varf(char e)
varf factor()
else
return x;
}
varf termen()
return x;
}
varf expresie()
return x;
}
String cod(varf x)
Mai ramâne de demonstrat optimalitatea codului obtinut în modul descris mai sus.
Propozitie În orice cod atasat unui arbore binar, #(STORE) este cel putin egal cu numarul vârfurilor al caror descendent drept nu este frunza.
Vom face demonstratia prin inductie dupa numarul n al vârfurilor din arbore.
Pentru n=1, afirmatia este evident adevarata.
Presupunem afirmatia din enuntul propozitiei adevarata pentru orice arbore cu cel mult n vârfuri si consideran un arbore cu n+1 vârfuri.
Daca descendentul drept al radacinii este o frunza, atunci numarul vârfurilor al caror descendent drept nu este frunza coincide cu numarul vârfurilor din subarborele stâng al caror descendent drept nu este frunza; cum acest subarbore are cel mult n vârfuri, putem aplica ipoteza de inductie.
Daca descendentul drept al radacinii nu este o frunza, atunci fie:
n= numarul vârfurilor din arbore al caror descendent drept nu este frunza;
s= numarul de instructiuni STORE din codul atasat arborelui;
n1= numarul vârfurilor din subarborele stâng al caror descendent drept nu este frunza;
s1= numarul de instructiuni STORE din codul atasat subarborelui stâng;
n2= numarul vârfurilor din subarborele drept al caror descendent drept nu este frunza;
s2= numarul de instructiuni STORE din codul atasat subarborelui drept.
Conform ipotezei de inductie avem: s1 n1 si s2 n2. Evident, n=n1+n2+1. Pe de alta parte în codul atasat arborelui mai trebuie introdusa cel putin o instructiune STORE, deci s s1+s2+1. Rezulta s n1+n2+1=n
Optimalitatea algoritmului prezentat rezulta acum din faptul ca el introduce o noua instructiune STORE numai pentru vârfurile al caror descendent drept nu este o frunza.
|
