Filtre numerice
III.1. Introducere
Filtrele numerice (FN) sunt sisteme liniare de tip discret implementabile la nivelul structurilor hardware de tip platforma PC, procesor de semnal, microcontroler.
Proiectarea unor astfel de structuri de tratare numerica include parcurgerea urmatoarelor etape:
Etapa specificatiilor de frecventa,
Etapa aproximarii specificatiilor de frecventa impuse prin determinarea efectiva a coeficientilor filtrului numeric,
Etapa realizarii diagramei structurale a FN,
Etapa analizei efectului lungimii finite a cuvintelor binare asociate valorilor numerice asupra performantelor FN,
Etapa implementarii filtrului dimensionat la nivelul suporturilor hardware ce au la baza microprocesoarele de uz general, procesoarele de semnal sau microcontrolerele.
In cadrul proiectarii filtrelor numerice destinate diferitelor aplicatii parcurgerea tuturor etapelor nu este strict necesara, exceptie facand etapa determinarii valor 414c27e ii coeficientilor filtrului numeric, ak si bl asociati ecuatiei cu diferente finite a filtrului numeric (FN).
![]() (1)
(1)
In ecuatia (1) y(n) reprezinta secventa numerica asociata iesirii filtrului numeric in timp ce x(n) reprezinta semnalul aplicat la intrarea filtrului numeric. Un alt mod de descriere a unui filtru numeric este cel bazat pe functia de transfer in "z" a FN, H(z).
Obtinerea lui H(z) se realizeaza prin aplicarea transformatei z ambilor membri ai ecuatiei (1). Astfel se obtine:
 (2)
(2)
|
Fig.3.1. Diagrama structurala in implementare directa, corespunzatoare ecuatiei cu diferente finite caracteristica filtrelor numerice |
Caracteristica H(z) a filtrelor numerice este usor reprezentabila la nivelul diagramei structurale asociate filtrului numeric. Elementele de baza a unei astfel de scheme structurale sunt celulele de intarziere sau de memorie, sumatoarele si multiplicatoarele. In cadrul diagramei structurale reprezentata in fig.3.1 se evidentiaza ponderea fiecarui tip de element in materializarea diagramei structurale asociata ecuatiilor (1) si (2).
In realizarea diagramei structurale s-au avut in vedere ecuatiile FN pentru cazul sistemelor cauzale. Un sistem numeric liniar este numit cauzal atunci cand pentru n<0, x(n)=0 si y(n)=0.
Semnificatia lui n=0 este cea de origine a axei timpului discret t=nTe. valorile negative ale lui n semnific[ practic timpi negativi, t=nTe, timpi ce nu corespund sistemelor reale de prelucrare numerica de semnal.
Pornind de la cele de mai sus se poate spune ca proiectarea filtrelor numerice reprezinta in principal, determinarea coeficientilor ak si bl astfel incat in final prin derularea algoritmului, esantioanele semnalului numeric de intrare x(n) sa fie modificate in deplin acord cu specificatiile de frecventa asociate primei etape ale proiectarii filtrelor numerice.
III.2. Clasificari ale filtrelor numerice
O prima clasificare are la baza caracteristicile amplitudine-frecventa (fig.3.2).
In figura 3.2 cu ft, ft1 si ft2 s-au notat frecventele de taiere asociate caracteristicilor.
Clasificarea FN functie de caracteristicile amplitudine-frecventa este urmatoarea:
Filtru numeric cu caracteristica de tip trece-jos (FN-TJ)
Filtru numeric cu caracteristica de tip trece-sus (FN-TS)
Filtru numeric cu caracteristica de tip trece-banda (FN-TB)
Filtru numeric cu caracteristica de tip opreste-banda (FN-OB)
O alta clasificare a FN are la baza criteriul ordinului filtrului, m. Indiferent de valoarea lui m, FN pot fi descompuse in structuri elementare de filtrare care se clasifica in:
Filtre numerice de ordinul I a caror ecuatie cu diferente finite este:
![]() (3)
(3)
Filtre numerice de ordinul II a caror ecuatie cu diferente finite este:
![]() (4)
(4)
|
Fig.3.2. Caracteristici aferente blocurilor de filtrare |
O alta clasificare a FN este bazata pe raspunsul la impuls a filtrului, h(nT). Tinand cont de acesta filtrele se clasifica in:
FN cu raspuns la impuls de durata finita (FIR - Finite Impulse Response). Aceste FN sunt caracterizate de un raspuns la impuls h(nT) de durata finita (h(nT) este dimensiune finita), adica:
![]() (5)
(5)
![]() (6)
(6)
N1>N2
FN cu raspuns la impuls de durata infinita (IIR - Infinite Impulse Response). Aceste filtre se caracterizeaza de catre un raspuns h(nT) de durata infinita, cu alte cuvinte nu exista valori finite pentru N1 si N2 astfel incat relatiile (5) si (6) sa fie satisfacute.
Un alt criteriu de clasificare este cel al modului in care sunt realizate. Astfel se disting doua tipuri de filtre numerice:
FN recursive pentru care marimea curenta de iesire depinde de valorile anterioare ale marimii de iesire (z(nTe-Te).y(nTe-iTe)), precum si de valorile curente si anterioare ale marimii de intrare (x(nTe).x(nTe-iTe)). Ecuatia caracteristica unor astfel de FN este:
![]() (7)
(7)
in relatie Te reprezinta perioada de esantionare, iar coeficientii ai si bI sunt coeficienti reali si constanti. Acest tip de FN este numit si FN cu memorie infinita.
FN nerecursive la aceste filtre marimea de iesire se exprima explicit in functie de valorile prezente si anterioare ale marimii de intrare conform relatiei:
![]()
Acest tip de FN este numit si FN cu memorie finita. Datorita structurii lor, mai sunt numite si filtre transversale.
Filtrele de tip FIR si IIR pot fi realizate atat in forma recursiva cat si nerecursiva. In mod uzual FN de tip FIR se realizeaza nerecursiv, iar FN de tip IIR se realizeaza recursiv.
Principalele avantaje ale filtrelor numerice (FN) sunt:
Dimensiuni reduse
Stabilitate termica - Variatiile de temperatura care in cazul filtrelor analogice (FA) influenteaza valorile rezistoarelor, condensatoarelor si bobinelor nu influenteaza in nici un fel filtrele numerice tinand cont ca implementarea acestora se face pe baza blocurilor integrate de tip sumator, multiplicator-acumulator.
Precizie ridicata - Imbunatatirea performantelor FN cum ar fi precizia, gama dinamica, stabilitatea si tolerantele caracteristicii amplitudine-frecventa pot fi obtinute prin cresterea numarului de biti ai reprezentarii valorilor numerice la nivelul registrilor.
Adaptabilitate - Raspunsul FN poate fi modificat in mod eficient prin introducerea unui nou set de coeficienti rezultat in urma proiectarii. In comparatie cu proiectarea in domeniul filtrarii analogice in care cresterea ordinului filtrului este limitata de complexitatea implementarii practice (numar mare de componente), in cazul filtrelor numerice nu exista o limitare stricta a ordinului maxim de filtrare.
Capacitatea de multiplexare - In conditiile in care frecventa semnalelor ce urmeaza a fi procesate nu impune utilizarea unei rate de esantionare ridicata filtrul numeric poate fi multiplexat in vederea utilizarii acestuia mai eficient. Spre exemplu in conditiile in care se urmareste prelucrarea mai multor semnale numerice aferente mai multor canale de masura se poate utiliza multiplexarea FN. Astfel esantioanele de intrare aferente diferitelor canale sunt multiplexate si transmise unitatii de prelucrare, spre exemplu un procesor de semnal TMS320C50 la nivelul caruia este implementat algoritmul de filtrare numerica.
Absenta problemelor legate de adaptarea de impedante
In comparatie cu filtrele analogice realizate in varianta activa sau pasiva se poate spune ca FN prezinta avantaje asimptotice. Se utilizeaza termenul asimptotic pentru a fi descrise avantajele care apar cand se impun niste performante foarte ridicate filtrelor. Spre exemplu daca trebuie realizat un filtru trece-jos cu f1=3000Hz cu un riplu de R=0.5dB si o atenuare la f=3005Hz egala cu At=90dB este absolut necesar ca structura de filtrare sa fie reprezentata de un filtru numeric.
Avantajele asimptotice rezulta si in cazul cand o necesita utilizarea unui numar mare de filtre. In acest caz cu o singura structura hard aferenta FN se pot implementa toate blocurile de filtrare numerica necesare, costul realizarii fiind acelasi pentru unul sau mai multe FN. Daca se utilizeaza filtrarea analogica diferite functii de filtrare sunt materializate de filtre analogice diferite ce contin componente diferite ceea ce conduce la cresterea costurilor. Un alt avantaj asimptotic apare atunci cand se cere un filtru cu o
complexitate extrema. Astfel un filtru analogic cu mai mult de 20 de poli este aproape imposibil de realizat spre diferenta de filtrele numerice.
Principalele dezavantaje ale FN sunt:
Banda de frecventa limitata - Aceasta limitare este strans legata de procesul de esantionare si conversie analog-numerica.
Erori datorate efectului lungimii finite a registrilor - Trecerea de la etapa de stabilire a valorilor coeficientilor la implementarea practica a acestora conduce ca urmare a limitarilor hardware la degradarea performantelor algoritmului proiectat. Aceasta degradare se datoreaza implementarii coeficientilor filtrului folosind registri de lungime finita.
III.3. Filtre Numerice cu Raspuns Finit la Impuls (FIR)
III.3.1. Generalitati
In exprimarea iesirii, y(n), a unei structuri de filtrare de tip IIR s-a evidentiat faptul ca aceasta depinde atat de valorile prezente si anterioare ale intrarii, cat si de valorile anterioare ale iesirii. In cazul filtrelor cu raspuns finit la impuls (FIR), semnalul numeric de iesire depinde doar de valorile prezente si anterioare ale semnalului de intrare. In aceste conditii ecuatia generala asociata unui filtru de tip FIR este:
![]() (9)
(9)
Valorile coeficientilor filtrului numeric sunt egale cu valorile raspunsului la impuls h(n) ale filtrului numeric.
Ca si in cazul filtrelor numerice cu raspuns infinit la impuls in continuare se va considera un exemplu care sa exprime concret caracteristicile filtrelor de tip FIR. Se considera astfel un FN dat prin ecuatia (9). Valorile lui h(n) se obtin prin aplicarea unui impuls unitar d(n) pe intrarea filtrului. Astfel h(n) se obtine pe baza relatiei:
![]() (10)
(10)
Tinand cont de relatia de definitie a lui d(n) rezulta:
![]() (11)
(11)
Marimile ce caracterizeaza din punct de vedere cantitativ complexitatea algoritmului de filtrare numerica pentru cazul filtrelor FIR sunt:
![]() - numarul de multiplicari pe
secunda
- numarul de multiplicari pe
secunda
![]() - numarul de adunari pe secunda
- numarul de adunari pe secunda
unde L este dat de ecuatia (9), iar fe este frecventa de esantionare.
O caracteristica a filtrelor de tip FIR este aceea ca, raspunsul la impuls h(n) este simetric si de aici creste viteza de procesare pe baza reducerii numarului de calcule aferente obtinerii lui h(n) la jumatate.
Nu acelasi lucru se intampla in cazul filtrelor IIR. In aceste conditii simetria valorilor coeficientilor FN poate reprezenta un criteriu de identificare a tipului FN, IIR sau FIR.
O alta precizare ce trebuie facuta este aceea ca FN de tip FIR sunt realizate in general sub forma filtrelor numerice cu baza liniara, filtre cu aplicabilitate sporita in domeniul practic.
Filtrele numerice de tip FIR sunt in general filtre nerecursive, semnalul numeric de iesire, y(nT), depinzand doar de valorile prezente si trecute ale semnalului numeric aplicat intrarii x(nT), x(nT-T), ., x(nT-iT).
Ca avantaje ale FN de tip FIR pot fi enumerate:
FN de tip FIR pot fi proiectate astfel incat caracteristica faza-frecventa sa fie liniara. Acest tip de caracteristica este de mare importanta in aplicatii in care distorsiunile de faza datorate fazei neliniare degradeaza informatia continuta in semnalul prelucrat x(n). Ca domenii in care FN de tip FIR prezinta o larga aplicabilitate pot fi mentionate: procesarea semnalului vocal, transmisia de date.
FN de tip FIR fiind de tip nerecursiv sunt prin definitie filtre stabile ceea ce prezinta un important avantaj in raport cu filtrele de tip IIR caracterizate prin stabilitate conditionata.
Eroarea de cuantizare legata de lucrul in aritmetica finita poate fi considerata neglijabila pentru aplicatii.
FN de tip FIR pot fi implementate in mod facil in cadrul sistemelor cu procesor de semnal.
FN de tip FIR sunt caracterizate printr-un ordin crescut in raport cu FN de tip IIR pentru satisfacerea aceleiasi caracteristici de frecventa impuse.
III.3.2. Metode de proiectare
Cea mai importanta caracteristica a filtrelor FIR este, prin definitie, lungimea finita a raspunsului la impuls. In plus, dupa cunoasterea acestuia, se poate obtine direct o forma de realizare, cunoscuta sub numele de filtru transversal. Acesta este motivul pentru care raspunsul la impuls joaca un rol central in diferitele metode de proiectare a filtrelor FIR. De asemenea, plecand de la raspunsul la impuls al filtrului RIF, se pune usor in evidenta liniaritatea sau neliniaritatea caracteristicii de faza a acestuia.
III.3.2.1. Proiectarea bazata pe TFSD si utilizarea ferestrelor de ponderare
Punctul de plecare al acestei metode este raspunsul in frecventa Hd(ejq , care se doreste realizat, in raport cu cel mai apropiat filtru FIR posibil. Cu ajutorul TFISD se deduce direct raspunsul la impuls ideal hd[n]. In general, totusi, nu se poate realiza practic imediat un filtru pe baza lui hd[n], deoarece:
a) hd[n] este de durata ("lungime") foarte mare sau chiar infinita, si
b) hd[n] este necauzal (adica hd[n]¹ pentru n<0).
Prin urmare trebuie:
a) limitata lungimea lui hd[n] la un numar de esantioane L acceptabil, si
b) introdus un decalaj ("intarziere") suficient pentru a obtine un raspuns la impuls cauzal.
Pentru proiectarea filtrelor se utilizeaza mai multe tipuri de ferestre:
fereastra dreptunghiulara:
![]() (12)
(12)
fereastra Barlett:
 (13)
(13)
fereastra Hanning:
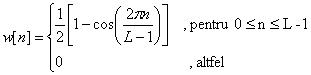 (14)
(14)
fereastra Hamming:
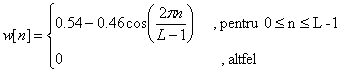 (15)
(15)
fereastra Blackman:
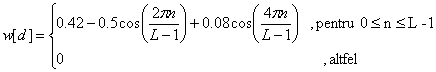 (16)
(16)
Ferestrele Kaiser formeaza o familie destul de speciala. Ele sunt definite dupa cum urmeaza:
 (17)
(17)
unde I0(x) este o functie Bessel, definita in modul urmator:
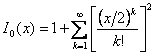 (18)
(18)
Forma exacta a ferestrei Kaiser se determina prin alegerea lui b : daca b creste, largimea benzii de tranzitie se mareste, dar ondulatiile se diminueaza. Pentru calculul functiei Bessel I0(x), nu este necesara utilizarea unui numar infinit de termeni ca la dezvoltarea in serie din relatia (18).
III.3.2.2. Metoda Seriilor Fourier
Metoda seriilor Fourier de proiectare a FN porneste de la premiza ca raspunsul in frecventa al oricarui filtru numeric este periodic in frecventa acesta conducand la posibilitatea dezvoltarii in serie Fourier. Seria rezultanta este de forma:
![]() (19)
(19)
iar imaginea in domeniul timp a lui H(ejw este:
![]() (20)
(20)
In relatia de mai sus h(n) reprezinta practic esantioanele raspunsului la impuls al filtrului numeric. Astfel iesirea FN se calculeaza cu relatia:
![]() (21)
(21)
Daca se considera ejw=z, din expresia (19) se obtine:
![]() (22)
(22)
Din pacate, aceasta dezvoltare este necauzala si infinita. Se va interveni astfel pentru eliminarea acestor doua neajunsuri.
Pentru o functie de transfer finita de dimensiune N, seria poate fi trunchiata considerand ca:
![]() (23)
(23)
![]() (24)
(24)
In acest caz se obtine:
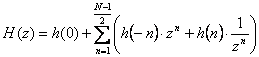 (25)
(25)
Pentru indeplinirea principiului cauzalitatii
se inmulteste H(z) cu ![]() obtinandu-se:
obtinandu-se:
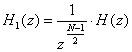 (26)
(26)
O asemenea
modificare este posibila, avand in vedere faptul ca raspunsul in amplitudine
ramane neschimbat, iar intarzierea de grup va creste cu o constanta egala cu ![]() .
.
In concluzie, aproximarea unui filtru ideal prin trunchierea raspunsului ideal la impuls este identica cu problema studierii convergentei seriilor Fourier.
Cel mai familiar aspect rezultat din studiul convergentei seriilor Fourier este fenomenul Gibbs. Acesta este reprezentat prin supracresterea in cazul unei functii treapta reprezentate printr-o serie Fourier trunchiata.
III.3.2.3. Metoda esantionarii in frecventa
Proiectarea FN de tip FIR pe baza Seriilor Fourier si a functiilor fereastra este o metoda simpla si intr-un anumit sens foarte generala. Cu toate acestea, sunt multe situatii cand este necesar ca filtrul proiectat sa fie cel mai bun ce poate fi obtinut pentru un ordin dat. In aceste conditii metoda esantionarii in frecventa reprezinta una din solutiile cele mai folosite.
Un filtru de tip FIR este determinat in mod unic fie de coeficientii raspunsului la impuls h(n), fie de coeficientii DFT, H(k). Presupunem ca obiectivul propus este de a determina coeficientii h(n) a unui FN de tip FIR a carui raspuns in frecventa este dat in figura 3.3.a. Coeficientii h(n) pot fi obtinuti aplicand transformata Fourier discreta inversa (DFT-1) esantioanelor H(k) din domeniul frecventa.
![]() (27)
(27)
|
|
unde H(k), k=0, 1, 2, ., N-1, sunt esantioanele aferente unui raspuns ideal in frecventa.
In cazul unui FN cu faza liniara pentru N par, unde N reprezinta dimensiunea lui H(k) se poate scrie:
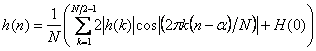 (28)
(28)
unde ![]() Pentru N
impar limita superioara de sumare este
Pentru N
impar limita superioara de sumare este ![]() .
Filtrul rezultat va fi caracterizat de un raspuns in frecventa identic cu
raspunsul filtrului ideal la momentele asociate esantioanelor prelevate insa
mult diferit intre esantioane (fig.3.3.c).
.
Filtrul rezultat va fi caracterizat de un raspuns in frecventa identic cu
raspunsul filtrului ideal la momentele asociate esantioanelor prelevate insa
mult diferit intre esantioane (fig.3.3.c).
Pentru obtinerea unei bune aproximari este necesar a se preleva un numar ridicat de esantioane. O a doua structura de filtrare rezulta esantionand raspunsul in frecventa a filtrului ideal la momente:
![]() (29)
(29)
Pentru un set de specificatii de frecventa date aplicarea uneia sau alteia din cele doua metode de proiectare FIR cu esantionare in frecventa conduce la obtinerea de caracteristici de filtrare diferite. In aceste conditii proiectantul va alege metoda care corespunde raspunsului frecvential optimal pentru aplicatia propusa.
III.3.2.4. Metoda optimizarii
|
| | 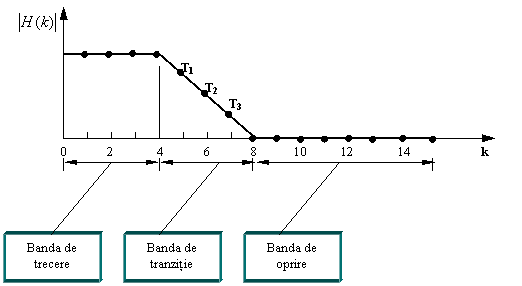 Fig.3.4. Esantioane frecventiale a unui FN-TJ cu trei esantioane inbanda de tranzitie a
caracteristicii
|
In vederea imbunatatirii raspunsului amplitudine-frecventa FN de tip FIR se propune o metoda de optimizare a proiectarii acestor filtre bazata pe esantionarea in banda de tranzitie a caracteristicii frecventiale. In figura 3.4 este prezentat cazul caracteristicii unui FN-TJ caracterizat prin trei benzi supuse esantionarii.
Pentru un filtru trece-jos, atenuarea in banda de oprire creste cu aproximativ 20dB pentru fiecare banda de frecventa esantionata. Aceasta crestere a atenuarii este insotita de o crestere a largimii benzilor de frecventa. Relatiile de corelatie intre numarul de benzi de tranzitie M si valoarea atenuarii si largimea benzii de tranzitie sunt:
![]() (30)
(30)
![]() (31)
(31)
In relatia (31) cu WBf s-a notat largimea benzii, cu N s-a notat dimensiunea lui h(n).
Valorile esantioanelor benzii de tranzitie care conduc la obtinerea unui optim in ceea ce priveste atenuarea in banda de oprire sunt determinate printr-un proces de optimizare. Un obiectiv de optimizare este acela de a gasi valorile esantioanelor aferente benzii de tranzitie T1, T2, .TM in vederea minimizarii riplului si cresterea atenuarii. Acest criteriu se exprima matematic:
![]() (32)
(32)
unde HD(w si H(w reprezinta raspunsul in frecventa al filtrului ideal respectiv raspunsul in frecventa al filtrului deja proiectat, iar W reprezinta un factor de ponderare. Pe baza conditiei (32) s-au stabilit tabele de valori ce include valorile lui T1, T2, T3, astfel incat sa se obtina optimul mentionat (fig.3.4). Valorile numerice ale lui T1, T2, T3 pentru cazul particulat N=15 sunt prezentate in tabelul de mai jos. In tabel BW se refera la numarul de esantioane din banda de trecere a FN.
|
BW |
At[dB] |
T1 |
T2 |
T3 |
|
|
1 tranz. | |||||
|
2 tranz. | |||||
|
3 tranz. |
In majoritatea cazurilor valorile considerate in cadrul benzii de tranzitie corespund:
unui esantion in banda de tranzitie
![]() 0.250<T1<0.450
0.250<T1<0.450
unui numar de doua esantioane in banda de tranzitie
0.040<T1<0.150
0.450<T2<0.650
unui numar de trei esantioane in banda de tranzitie
0.003<T1<0.035
0.100<T2<0.300
0.550<T3<0.750
|
|
Valorile scazute sunt pentru FN de banda larga si conduc la o atenuare ridicata in banda de oprire. Efectul obtinut prin utilizarea unui numar de unul, doua sau trei esantioane in banda de tranzitie a FN este exprimat grafic in figura 3.5.
In figura 3.5.a este prezentata H(f) pentru cazul in care nu sunt prelevate esantioane din banda de tranzitie a caracteristicii ideale H(k) a filtrului. Figurile 3.5.b, c, d sunt asociate prelevarii unui numar de unu, doua sau trei esantioane frecventiale din banda de tranzitie a filtrului de proiectat. Se observa ca nivelul ondulatiilor scade odata cu cresterea numarului de esantioane prelevate.
III.4. Filtre numerice cu Raspuns Infinit la Impuls (IIR)
III.4.1. Generalitati
Raspunsul unui FN de tip IIR depinde de valorile prezenta si trecute ale esantioanelor secventei numerice de intrare x(n) precum si de valorile trecute ale semnalului de iesire. Astfel la modul general ecuatia ce caracterizeaza un astfel de filtru este data de:
![]() (33)
(33)
Pentru simplificare in continuare se va omite notarea explicita a perioadei de esantionare Te in cadrul ecuatiilor notatiile folosite fiind:
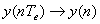 (34)
(34)
![]() (35)
(35)
Se considera un FN de ordin I. Ecuatia (33) in acest caz devine:
![]() (36)
(36)
Cunoasterea structurii de filtrare numerica coincide cu determinarea raspunsului la impuls unitar, d(n) al FN, h(k) (fig. 3.6).
|
h(k), k=0, 1, 2, . (raspuns la impuls) x(n) y(n) secventa de intrare secventa de iesire Fig. 3.6. Reprezentarea conceptuala a FN |
Se considera astfel x(n)= d(n), iar y(n) va deveni h(n), se obtine astfel:
![]() (37)
(37)
Tinand cont de cauzalitatea filtrului se urmareste determinarea h(n) din aproape in aproape.
Pentru n=0
![]() (38)
(38)
n=1
![]() (39)
(39)
n=2
![]() (40)
(40)
![]()
n=k
![]() (41)
(41)
Analizand relatiile (38)-(41) rezulta
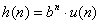 (42)
(42)
Acest rezultat a fost obtinut in maniera inductiva prin calculul iesirii filtrului numeric de tip IIR pentru valori consecutive ale intrarii. Rezultatele obtinute sunt prezentate in tabelul ce urmeaza:
|
N |
d(n) |
|
|
b |
||
|
b2 |
||
|
b3 |
||
|
b4 |
||
|
n |
bn |
|
Fig.3.7 Diagrama structurala a celulei de filtrare de ordin I tip IIR |
Raspunsul la impuls a filtrului de ordin I propus
Diagrama structurala aferenta filtrului numeric anterior definit este data in figura 3.7.
In diagrama se evidentiaza:
1 bloc de multiplicare (multiplicare cu coeficientul b al FN),
1 bloc de intarziere care in planul variabilei complexe z corespunde multiplicarii z-1,
1 bloc de sumare.
Cativa din parametrii utilizati pentru a exprima in maniera cantitativa complexitatea algoritmului de filtrare sunt:
MPS - numarul de multiplicari pe secunda care in cazul FN de tip IIR se calculeaza cu relatia:
![]() (43)
(43)
unde P si M sunt definite in relatia (33).
APS - numar de adunari pe secunda care in cazul filtrelor numerice de tip IIR se calculeaza cu relatia:
![]() (50)
(50)
In relatiile de mai sus fe reprezinta frecventa de esantionare asociata structurilor de filtrare numerica.
III.4.2. Tehnici de proiectare a FN de tip IIR
Abordarea cea mai intalnita in proiectarea filtrelor numerice de tip IIR este cea a determinarii pe baza diagramei de tolerante a unui filtru analogic prototip, filtru ce va fi supus ulterior transformarii in FN caracterizat de o caracteristica de frecventa identica. Aceasta modalitate de proiectare se bazeaza pe urmatoarele experiente:
Proiectarea filtrelor analogice este pe deplin cunoscuta astfel incat proiectarea unui astfel de filtru este facila;
Numeroase metode de proiectare a filtrelor analogice (FA) sunt bazate pe seturi de relatii usor implementabile la nivelul unui soft de proiectare si in acelasi timp usor transferabile catre proiectarea filtrelor numerice de tip IIR (Infinite Impulse Response);
In numeroase aplicatii se impune utilizarea filtrelor numerice pentru simularea performantelor filtrelor analogice.
Metodele principale de proiectare a FN pe baza FA prototip pentru o diagrama de tolerante data sunt:
Metoda invariantei impulsului,
Metoda transformatei biliniare.
III.4.2.1. Metoda invariantei impulsului
In cadrul acestei metode se porneste de la un filtru analogic (FA) caracterizat de raspunsul la impuls ha(t), raspunsul in frecventa Ha(w si de functia de transfer Ha(s).
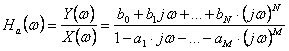 (51)
(51)
![]() (52)
(52)
Relatia de legatura intre s si w este:
![]() (53)
(53)
Pornind de la marimile caracteristice filtrului analogic prototip care satisfac diagrama de tolerante, obiectivul impus in proiectarea FN prin metoda invariantei impulsului este ca raspunsul la impuls a filtrului IIR, hd(n) sa satisfaca relatia:
![]() (54)
(54)
in care Te reprezinta perioada de esantionare a sistemului discret. In acest caz relatia de legatura intre functia de transfer a sistemului discret si cea a sistemului analogic este:
![]() (55)
(55)
Legatura dintre raspunsurile la impuls precum si dintre functia de transfer a sistemului discret si a celui continuu este prezentata in figura 3.8.
Analizand imaginile frecventiale ale raspunsurilor la impuls pentru sistemul continuu si cel discret se observa ca imaginea frecventiala a lui hd(n) depinde hotarator de valoarea perioadei de esantionare aferenta sistemului discret, alegerea necorespunzatoare a lui T conducand la aparitia fenomenului de aliasing, fenomen exprimat in figura.
|
Fig 3.8. Reprezentarea schematica a ha(t), hd(n)= ha(nT), Ha(ω) si a lui Hd(ejθ) |
Determinarea coeficientilor filtrului numeric de tip IIR
Se considera functiile de transfer respectiv caracteristica de frecventa aferente unei diagrame de tolerante impuse prin tema de proiectare.
![]() (56)
(56)
Raspunsul la impuls ha(t) se obtine prin aplicarea transformatei Laplace inversa, L-1 lui Ha(s).
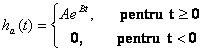 (57)
(57)
In aceste conditii raspunsul sistemului discret corespunzator aceleasi scheme de tolerante este:
![]() (58)
(58)
Aplicand transformata in z raspunsului la impuls a sistemului discret rezulta functia de transfer in z a acestuia.
![]() (59)
(59)
Prin aplicarea transformatei z-inversa (z-1) ambilor termeni ai ecuatiei (59) se va obtine ecuatia cu diferente finite (60) care caracterizeaza sistemul numeric:
![]() (60)
(60)
![]() (61)
(61)
![]() (62)
(62)
![]() (63)
(63)
Implementarea la nivelul hardware-ului a filtrului numeric proiectat impune realizarea diagramei structurale a filtrului numeric de ordin I obtinut in urma proiectarii. Astfel in figura 3.9 este prezentata diagrama structurala a FN mai sus prezentat.
|
Fig.3.9. Diagrama structurala a filtrului numeric de ordinul I |
In continuare se impune a fi analizate functiile de transfer, Ha(s), respectiv discrete Hd(z), exprimate in (56) si (58).
Astfel se observa ca Ha(s) prezinta un pol pentru
s=B, in timp ce Hd(z)
prezinta un pol z=eBT. Aceasta
constatare exprima de fapt o proprietate importanta a acestei metode de
proiectare si anume faptul ca polii simpli pentru filtrul analogic s=pk sunt convertiti in poli
simpli ai filtrului numeric, valorile acestora fiind ![]() .
.
In general pornind de la o structura de filtrare analogica data prin functia de transfer in s:
![]()
se obtine o functie de transfer a sistemului discret de tipul:
![]()
Conversia ecuatiilor filtrului analogic prototip in FN atrage dupa sine trecerea polilor FA in poli ai FN si totodata conversia unui FA stabil intr-un FN stabil.
Concluzii - Metoda invariantei impulsului
Raspunsul la impuls a filtrului digital, h(nT), este identic cu cel al filtrului analogic, h(t), la momente discrete de timp, t=nT, n=0,1,.
Frecventa de esantionare afecteaza raspunsul in frecventa a filtrului proiectat prin aceasta metoda. Astfel se impune lucrul cu frecvente de esantionare suficient de ridicate, fe=20fmax, astfel incat raspunsul in frecventa a filtrului numeric sa fie cat mai apropiat de cel al filtrului analogic.
In conditiile esantionarii semnalului de prelucrat, spectrul raspunsului la impuls a FN proiectat prin metoda prezentata reprezentat prin H(z) va fi acelasi cu cel al filtrului analogic prototip Ha(s) dar se repeta la multipli intregi ai frecventei de esantionare.
Metoda se utilizeaza in proiectarea FN cu banda de tranzitie ingusta de tip FN-TJ cu nivel redus de aliasing in conditiile utilizarii unei frecvente ridicate de esantionare dar este nerecomandata in proiectarea FN-TS si FN-OB pentru care este necesara introducerea suplimentara in cadrul lantului de prelucrare a unui filtru anti-aliasing.
III.4.2.2. Metoda transformatei biliniare
Prezentarea metodei
Metoda transformatei biliniare (TB) este una din cele mai folosite metode pentru proiectarea filtrelor numerice de tip IIR, pornind de la filtrul analogic prototip. Odata proiectat FA pornind de la un set de specificatii de frecventa date Transformata biliniara este folosita pentru realizarea trecerii de la planul complexe asociata sistemelor de tip continuu, s, la variabila de tip complex asociata sistemelor de tip discret, z.
Relatiile de legatura intre s si z sunt:
![]() (66)
(66)
Grafic aceasta relatie de legatura intre s si z este exprimata in figura 3.10.
|
Fig.3.10 Diagrama corespondentelor dintre planul variabilei s si planul variabilei z |
Sinteza privind procedura de proiectare a IIR folosind transformata biliniara
Etapele principale ale metodei:
Etapa 1 Stabilirea functiei de transfer a FA, H(s), pe baza specificatiilor de frecventa
Etapa 2 Determinarea pulsatiei de taiere a FN, ωd
Etapa 3 Determinarea pulsatiei de taiere echivalenta pentru FA, ωa
![]() (67)
(67)
Etapa 4 Denormalizarea caracteristicii H(s) prin realizarea substitutiei
![]() (68)
(68)
Etapa 5 Aplicarea transformatei biliniare pentru obtinerea lui H(z)
![]() (69)
(69)
III.5. Tipuri de filtre analogice prototip
Deoarece in multe cazuri studiul filtrelor numerice se face plecand de la filtrele analogice, se vor prezenta pe scurt principalele tipuri de filtre trece-jos analogice. Astfel pot fi mentionate:
Filtrele analogice Butterworth
Filtrele Cebisev (direct si invers)
Filtrele eliptice
Toate aceste filtre anterior prezentate aproximeaza o caracteristica de atenuare dreptunghiulara in banda de trecere.
III.5.1. Filtrul Butterworth
Filtrul Butterworth realizeaza o caracteristica de amplitudine-frecventa monotona fiind caracterizata prin lipsa ondulatiilor in banda de trecere si in banda de oprire. Relatia care caracterizeaza acest tip de filtru este:
 (70)
(70)
In relatia de mai sus n repreyinta ordinul filtrului, ω t reprezinta pulsatia de taiere la 3dB. Caracteristica amplitudine frecventa a filtrului este data in figura 3.11.a.
Atenuarea in banda de oprire At asociata FA se calculeaza cu relatia:
![]() (71)
(71)
Dependenta dintre valorile deviatiilor in banda de trecere δ1, in banda de oprire δ2 si ordinul filtrului analogic este exprimata prin relatia:
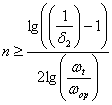 (72)
(72)
Polii functiei de transfer, pk sunt plasati in planul s, pe un cerc de raza ω t. Relatia de calcul a valorilor acestora este:
![]() (73)
(73)
k=1, 2, , n
III.5.2. Filtrul Cebisev
Filtrul Cebisev este un filtru care admitand ondulatii in banda de trecere si utilizand acelasi numar de poli si zerouri ca si filtrul Butterworth poate realiza o caracteristica de frecventa cu o panta mai abrupta in jurul frecventei de taiere, ωt. Relatia care exprima patratul modulului functiei de transfer a acestui tip de FA este:
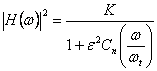 (74)
(74)
In relatia de mai sus n repreyinta ordinul filtrului analogic, Cn reprezinta un polinom Cebisev de ordin n, iar e reprezinta un parametru ce caracterizeaza riplul FA (ondulatiile in banda de trecere a FA). Polinomul Cn este dat sub forma recurenta:
C1(x)=x
C2(x)=2x2-1
Cn+1(x)-2xCn-1=0
Riplul filtrului, R, de parametru e se calculeaza cu relatia:
![]() (76)
(76)
Atenuarea FA in banda de oprire se calculeaza cu relatia:
![]() (77)
(77)
Relatia de calcul al ordinului FA de tip Cebisev in conformitate cu valorile tolerantelor in banda de trecere si in banda de oprire este:
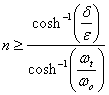 (78)
(78)
|
Fig.3.11. Caracteristicile amplitudine frecventa pentru FA de tip Butterworth, Cebisev Invers si Eliptic |
Polinomul Cebisev se caracterizeaza prin ondulatiile egale pentru x variind intr-un domeniu dat. Prin specificarea lui e, caracteristica de frecventa prezinta ondulatii egale in banda de trecere si o cadere monotona in banda de oprire.
Polii FA Cebisev sunt plasati pe o elipsa coordonatele acestora fiind:
![]() (79)
(79)
unde:
![]() (80)
(80)
III.5.3. Filtrul eliptic
Filtrul eliptic realizeaza cu o precizie mai mare frecventa de taiere decat filtrul Cebisev admitand totodata ondulatii atat in banda de trecere, cat si in banda de oprire. Relatia care exprima patratul modulului functiei de transfer a acestui tip de FA este:
![]() (81)
(81)
In relatie Gn este o functie Cebisev de tip rational. Caracteristica filtrului eliptic este prezentata prin comparatie cu celelalte tipuri prezentate in figura 3.11.d.
Calculul coeficientilor FN-TS, FN-TB, FN-OB de tip IIR
Etapele necesare in stabilirea valorilor coeficientilor FN de tip IIR sunt:
Determinarea functiei de transfer in s normalizata, H(s) a filtrului analogic prototip pornind de la specificatiile de frecventa aferente FN de proiectat.
Determinarea frecventelor critice a FN. Pentru FN-TS exista o singura frecventa critica f1 in timp ce pentru FN-TB si FN-OB exista un set de doua frecvente critice, ft1 si ft2.
Substituirea variabilei complexe s in functia de transfer H(s) folosind una din urmatoarele transformari ce depind de tipul filtrului (FN-TJ, FN-TS, FN-TB, FN-OB)
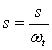 FN-TJ FN-TJ (82)
FN-TJ FN-TJ (82)
![]() FN-TJ FN-TS (83)
FN-TJ FN-TS (83)
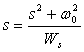 FN-TJ FN-TB (84)
FN-TJ FN-TB (84)
![]() FN-TJ FN-OB (85)
FN-TJ FN-OB (85)
unde ![]() ,
iar
,
iar 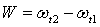 .
.
Aplicarea transformatei biliniare pentru functia de transfer in s denormalizata H1(s)
![]() (86)
(86)
|