Graf complet si graf bipartit

Graf complet si graf bipartit

Definitie: Se numeste graf complet cu n vârfuri, notat K_n, un graf G=(X,U) cu proprietatea ca oricare doua vârfuri sunt adiacente, adica (") x,y X ) muchia [x,y] U.

Exemplu:

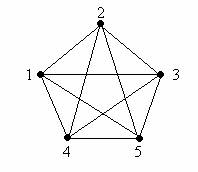Figura 5.

Teorema

Un graf complet cu n vârfuri are muchii

Ne putem convinge usor de adevarul afirmatiei 959d34j imaginând urmatorul procedeu de numarare a muchiilor.

Pornim de la primul vârf si trasam n-1 muchii. Apoi consideram al doilea vârf si obtinem de asemenea n-1 muchii. Deoarece procedeul se poate aplica pentru fiecare din cele n vârfuri, obtinem n(n-1) muchii. Desigur, în acest fel am numarat fiecare muchie de 2 ori, si anume de fiecare data când am luat în considerare un capat al ei. În consecinta un graf complet cu n vârfuri are exact muchii.

Definitie: Se numeste graf bipartit, un graf G=(X,U) cu proprietatea ca exista doua multimi A si B incluse în X, astfel încât:

A B = , A B = X,

toate muchiile grafului au o extremitate în A si cealalta în B.

Exemplu:

Fie G=(X,U), unde: X= , U=

Cu multimile A= si B= , generam graful bipartit de mai jos.

Se observa ca: A B = , A B = X, iar fiecare muchie are o extremitate în A si o  extremitate în B.

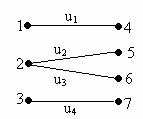
Figura 6.

Definitie: Se numeste graf bipartit complet, un graf bipartit cu proprietatea ca pentru orice vârf x din A si orice vârf y din B, exista muchia (x,y) (unde A si B sunt cele doua submultimi care partitioneaza multimea vârfurilor x).

Exemplu:

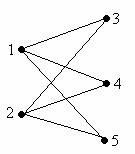
Figura 7.

V. Notiunile de lant si ciclu

Definitie: Se numeste lant în graful G, o succesiune de vârfuri L=(z₁,z₂,.......,z_k), unde z₁,z₂,.......,z_k X, cu proprietatea ca oricare doua vârfuri consecutive sunt adiacente, adica muchiile [z₁,z₂],[z₂,z₃],......,[z_k-1,z_k] U.

Vârfurile z₁ si z₂ se numesc extremitatile lantului, iat numarul de muchii care intra în componenta sa reprezinta lungimea lantului.

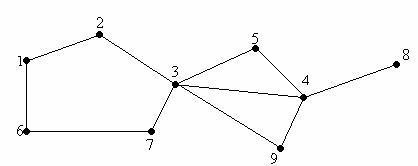
Figura 8.

Exemplu:

În graful din fugura 8, putem distinge lanturile: L₁=(1,2,3,5,4,8), L₂=(1,2,3,2), L₃=(9,3,5,4,3,2), L₄=(6,7,3,5,4,8).

Un lant poate fi interpretat ca un treaseu care pleaca din vârful z₁ si ajunge în vârful z_k, trecând prin mai multe vârfuri si parcurgând mai multe muchii.

Daca vârfurile z₁,z₂,.......,z_k sunt distincte doua câte doua, lantul se numeste lant elementar. În caz contrar este ne-elementar.

Exemplu:

Lantul L₄ din exemplul anterior este elementar, pentru ca nici un vârf nu apare de doua ori. La fel lantul L₁. în schimb lanturile L₂ si L₃ sunt ne-elementare.

Definitie: Se numeste ciclu într-un graf, un lant L=( z₁,z₂,.......,z_k) cu proprietatea ca z₁=z_k si muchiile [z₁,z₂],[z₂,z₃],......,[z_k-1,z_k] sunt distincte doua câte doua.

Exemplu:

Graful din figura 8 c₁=(3,4,5,3,7,6,1,2,3), c₂=(1,2,3,7,6,1), c₃=(3,5,4,9,3) sunt cicluri. De exemplu, c₃ este ciclu, deoarece traseul pe care îl descrie porneste din vârful 3 si ajunge tot în vârful 3, si în plus muchiile [3,5], [5,4], [4,9] si [9,3] sunt distincte doua câte doua (nu apare aceeasi muchie de mai multe ori).

Daca într-un ciclu, toate vârfurile cu exceptia primului si a ultimului sunt distincte doua cate doua, atunci ciclul se numeste ciclu elementar. În caz contrar, el este ne-elementar.

Exemplu:

Ciclurile c₂ si c₃ din exemplul anterior sunt elementare, iar c₁ este ne-elementar (în c₁, vârful 3 apare si ca vârf "intermediar", adica traseul descris mai trece odata prin vârful 3 pe lânga faptul ca porneste din el si se întoarce tot în el).