Grafuri hamiltoniene si euleriene
Definitie: Se numeste ciclu hamiltonian într-un graf, un ciclu elementar care contine toate vârfurile grafului.
Definitie: Se numeste graf hamiltonian, un graf care contine un ciclu hamiltonian.
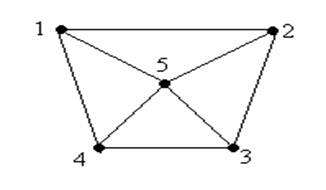
Figura 11.
Exemplu:
Graful din figura 11. este hamiltonian, deoarece ciclul c=[1,2,3,5,4,1] este elementar (pleaca din vârful 1, iar muchiile [1,2], [2,3], [3,5], [5,4] si [4,1] sunt distincte doua câte doua ) si în plus contine toate vârfurile.
Definitie: Se numeste lant hamiltonian într-un graf, un lant elementar care contine toate vârfurile grafului.
Teorema
Daca într-un graf G=(X,U) cu n> 3 vârfuri, gradul fiecarui vârf x verifica conditia d(x)> n/2, atunci graful este hamiltonian.
Definitie: Se numeste ciclu eulerian într-un graf, un ciclu care contine toate muchiile grafului.
Definitie: Se numeste graf eulerian, un graf care contine un ciclu eulerian.
Exemplu:
Pentru graful din figura 12. ciclul c=[1,2,3,6,7,8,3,4,5,1] este eulerian, deoarece pleaca din vârful 1 si se termina tot în vârful 1, iar muchiile sale consecutive, adica [1,2], [2,3], [3,6], [6,7], [7,8], [8,3], [3,4], [4,5], [5,1], sunt distincte doua câte doua (altfel spus, ciclul nu trece de doua ori prin aceeasi muchie).
Teorema:
Un graf fara vârfuri izolate este eulerian, daca si numai daca este conex, si gradele tuturor vârfurilor sunt numere pare.
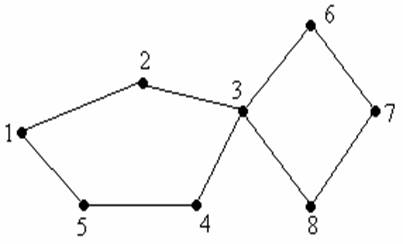
Figura 12.
|