Def.1: Un graf neorientat este o pereche ordonata G=(X, ); unde X este o multime finita si masurabila, nevida de elemente care se numesc virfuri sau noduri, iar este o multime de perechi neordonate de elemente distincte din X numite muchii.
Daca X este finita atunci se utili 737j96h zeaza notatia /x/ sau #x sau card(x)=n , cu semnificatia: "cardinalitatea lui X este n", unde n reprezinta numarul virfurilor grafului . O muchie avind virfurile "i" si "j" numite extremitatile sale, este notata cu (i,j).
Consideram graful neorientat H=(Y,Γ1)de cardinalitate m (#y=m), spunem ca el este un subgraf al grafului G=(X,Γ) de cardinalitate n (#x=n) cu proprietate ca n>m daca H se poate obtine din G prin eliminarea unui numar finit de virfuri si a muchiilor incidente in acele virfuri.
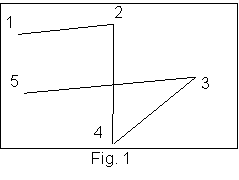Ex: Fie
graful G=(X,Γ) cu cardinalitate 5 #X=5,
reprezentat in figura 1.
Def. 2:Un subgraf
al lui G este un graf H=(Y,Γ1) unde Y
X si Γ1 este
formata din toate muchiile lui Γ
care unesc virfuri din Y.
Def. 3:Un graf G =(X, ) , unde , se numeste subgraf al grafului G.
Def.4: Se numeste lant o succesiune de muchii de forma (i1,i2), (i2,i3),.,(in-1,in), notata prescurtat (i1,i2,,in).
Def.5: Numarul total al muchiilor care constituie lantul se numeste lungimea lantului.
Def.6: Un lant ale carui virfuri sunt distincte se numeste lant elementar.
Def.7: Daca (i1,i2,,in),n ≥ 3, este lant elementar, atunci (i1,i2,,in,i1) se numeste ciclu elementar.
Def.8: Un lant (i1,i2,,in i1) care contine cel putin un ciclu elementar se numeste ciclu.
Def.9: Un virf care este extremitatea unei singure muchii se numeste virf terminal.
Def.10: Doua virfuri unite printr-o muchie se numesc adiacente , extremitatile unei muchii fiind adiacente muchiei respective.
Def.11: Un graf neorientat G se numeste conex daca oricare doua virfuri ale sale sunt unite cel putin printr-un lant.
Exemple:
In fig.2 (1,2,3) si (1,4,3) sunt lanturi ce unesc virfurile 1 si 3, iar (1,2,3,4,1) este un ciclu. Graful din fig. 2 este conex, pe cind graful din fig.3 este neconex.
Def.12: Un subgraf conex, in care nici un virf din subgraf nu este unit cu unul din afara printr-o muchie a grafului initial, se numeste subgraf conex maximal sau componenta conexa.
Impartirea
unui graf in componentele sale conexe determina o partitie a lui X si una a lui
. Astfel, pentru
graful din fig.5, se poate scrie : X =
.
|
