Heap-uri binomiale si Fibonacci
În acest capitol vom învata:
Ce sunt arborii binomiali
De ce se numesc asa
Ce sunt heap-urile binomiale
Ce este analiza amortizata
Ce sunt heap-urile Fibonaci
De ce sunt superioare heap-urile Fibonacci
13.1 Despre necesitatea unor altfel de structuri
Multimea, ca notiune fundamenatala, este la fel de importanta în informatica ca si în matematica. În timp ce multimile matematice sunt nemodificabile, multimile manipulate de algoritmi pot creste, descreste sau, în restul cazurilor, se pot modifica în timp. Astfel de multimi se numesc dinamice. În functie de algoritmi, sunt necesare diferite timpuri de operatii pentru a fi executate asupra multimilor. De exemplu, multi algoritmi au nevoie doar de posibilitatea de a insera elemente într-o multime, de a sterge elemente dintr-o multime sau de a testa apartenenta la o multime. Alti algoritmi necesita operatii mai complicate. De exemplu, cozile de prioritate suporta operatiile de inserare a unui element si extragere a celui mai mic element dintr-o multime. Deci nu e surprinzator faptul ca cea mai buna modalitate de a implementa o multime dinamica depinde de operatiile pe care trebuie sa le ofere.
Într-o implementare tipica a unei multimi dinamice, fiecare element este reprezentat de un obiect ale carui câmpuri pot fi examinate si manipulate daca avem un pointer (o referinta) la acel obiect. Unele categorii de multimi dinamice presupun ca un câmp al obiectului este un câmp cheie, de identificare. Daca toate cheile sunt diferite, multimea dinamica poate fi privita ca o multime de valori ale cheilor. Obiectul poate contine date aditionale, care sunt gestionate în alte câmpuri ale obiectului, dar sunt de fapt neutilizate de catre implementarea multimii. De asemenea, obiectul poate avea câmpuri ce sunt manipulate de catre operatiile multimilor, aceste câmpuri putând contine date sau referinte spre alte obiecte din multime. Unele multimi dinamice presupun ca valorile cheilor sunt alese dintr-o multime total ordonata, ca de exemplu, multimea numerelor reale. O ordine totala ne permite sa definim, de exemplu, cel mai mic element în multime sau sa vorbim despre urmatorul element mai mare decât un element dat din multime.
Operatiile pe o multime dinamica pot fi împartite în doua categorii: interogari, care returneaza informatii despre multime sau operatii de modificare, care modifica multimea.
Exista structuri de date simple ca: stive, cozi, liste înlantuite si arbori cu radacina, tabele de dispersie (hash).
O alta structura de date importanta sunt arborii de cautare binara care au rol de baza pentru multe alte structuri de date. Arborii rosu-negru, sunt o varianta a arborilor de cautare binara. Un arbore rosu-negru este un arbore de cautare echilibrat ca si un alt tip de arbore de cautare echilibrat numit B-arbore.
O alta structura de date importanta este ansamblul (heap-ul). Heapsort introduce o tehnica noua de proiectare a algoritmilor bazata pe utilizarea unei structuri de date, numita heap. Structura de date heap este utila nu doar pentru algoritmul heapsort, ea poate fi la fel de utila si în tratarea eficienta a unei cozi de prioritate.
Termenul heap a fost introdus si utilizat initial în contextul algoritmului heapsort, dar acesta se foloseste si în legatura cu alocarea dinamica, respectiv în tratarea memoriei bazate pe "colectarea reziduurilor", de exemplu, în limbajele de tip Lisp.
Prezentam în continuare sructurile de date avansate: heap-uri binomiale si operatiile care se executa pe heap-uri: creare, gasirea cheii minime, reuniunea a doua heap-uri binomiale, inserarea unui nod, extragerea nodului având cheia minima si descresterea unei chei.
B-arborii, care sunt arbori echilibrati folositi la memorarea pe disc magnetic. Deoarece discul magnetic opereaza mult mai încet decât memoria RAM, performantele B-arborilor vor fi masurate nunumai prin timpul consumat cu operatiile de cautare dinamice, ci si prin numarul de accese la disc efectuate. Pentru fiecare operatie numarul de accese la disc este proportional cu înaltimea B-arborelui.
Heap-urile binomiale executa operatiile: INSEREAZĂ, MINIMUM, EXTRAGE-MIN si REUNEsTE în cazul cel mai defavorabil, în timp O(lg n), unde n este numarul total de elemente din heap-ul de intrare (sau în cele doua heap-uri de intrare în cazul REUNEsTE). Pe structura de date heap binomial se pot executa si operatiile sTERGE si DESCREsTE-CHEIE.
Heap-urile Fibonacci sunt superioare heap-urilor binonmiale, cel putin în sens teoretic. Pentru masurarea performantelor heap-urilor Fibonacci se folosesc margini de timp amortizate. Operatiile INSEREAZĂ, MINIMUM si REUNEsTE consuma în caul heap-urilor Fibonacci, timp amortizat de numai O(1), în timp ce EXTRAGE-MIN si sTERGE consuma un timp amortizat de O(lg n). Cel mai mare avantaj al heap-urilor Fibonacci este acela ca DESCREsTE-CHEIE consuma un timp amortizat de numai O(1). Operatia DESCREsTE-CHEIE definita pentru heap-urile Fibonacci este asimptotic mai slaba decât operatiile similare la diversii algoritmi specifici de grafuri, motiv pentru care acestia o folosesc mai rar.
O alta categorie de structuri de date avansate o reprezinta structurile de date pentru multimi disjuncte. Se da un univers de n elemente care sunt grupate în multimi dinamice. Initial, fiecare element este singur într-o multime. Operatia reuneste fuzioneaza doua multimi, iar cererea GĂSEsTE-MULŢIME identifica multimea care contine un anumit element la un moment dat. Reprezentând fiecare multime printr-un arbore cu radacina, vom obtine operatii surprinzator de rapide: o secventa de m operatii se executa în timp O(ma(m,n)), unde a(m,n) este cel mult 4.
Printre altele sunt incluse si urmatoarele struc 757j94h turi:
O structura de date, inventata de van Emde Boas, care admite operatiile MINIMUM, MAXIMUM, INSEREAZĂ, sTERGE, CAUTĂ, EXTRAGE-MIN, EXTRACT-MAX, PREDECESOR, SUCCESOR. Acestea, în multimea de chei necesita, în cel mai defavorabil caz, timpul O(lg lg n).
Arborii dinamici, definiti de catre Sleator si Tarjan. Cu ajutorul lor se întretine o padure de arbori cu radacini disjuncte. Fiecare arc din fiecare arbore are atasat, drept cost, un numar real. În arborii dinamici se pot efectua operatii în vederea aflarii parintilor, radacinilor, costurilor arcelor, costului minim al unui drum de la un nod la o radacina. Arborii pot fi manevrati prin taierea de arce, modificarea costurilor arcelor de pe un drum de la un nod la o radacina, legarea unei radacini la un alt arbore etc. Una din implementarile arborilor dinamici necesita un timp amortizat de O(lg n) pentru fiecare operatie.
Arborii splay (oblici), dezvoltati de catre Sleator si Tarjan, sunt un tip de arbori binari de cautare care dau un timp amortizat O(lg n) pentru toate operatiile standard. Una dintre aplicatiile acestor arbori permite simplificarea arborilor dinamici.
Structurile de date persistente permit atât cereri, cât si, uneori, actualizari ale versiunilor vechi ale structurii. Tehnicile de creare a structurilor de date înlantuite persistente, descrise de catre Driscoll, Sarnak, Sleator si Tarjan, sunt eficiente deoarece consuma foarte putin timp si spatiu.
13.2 Heap-uri binomiale
Heap-urile binomiale fac parte din structurile de date cunoscute sub numele de heap-uri interclasabile, caracterizate de urmatoarele operatii:
CREEAZĂ-HEAP(H) creeaza si returneaza un heap nou care nu contine elemente.
INSEREAZĂ(H,x) insereaza nodul x a carui cheie a fost initializata în heap-ul H.
MINIMUM(H,y) returneaza un pointer la nodul cu cea mai mica cheie din H
EXTRAGE-MIN(H) sterge nodul cu cheia minima din H si returneaza un pointer la acest nod.
REUNEsTE(H1,H2,H) creeaza si returneaza un heap nou care contine toate nodurile heap-urilor H1 si H2. Heap-urile H1 si H2 sunt "distruse" în urma acestei operatii.
DESCREsTE-CHEIE(H,x,k) atribuie nodului x din heap-ul H valoarea k pentru cheie, valoare presupusa a nu fi mai mare decât valoarea curenta a cheii.
sTERGE(H,x) sterge nodul x din heap-ul H.
Tabelul de mai jos arata ca heap-urile binare obisnuite, folosite, de exemplu, în heapsort, suporta bine aceste operatii, cu exceptia operatiei REUNEsTE. În cazul heap-urilor binare, pentru fiecare operatie, exceptând REUNEsTE, tipul de executie în cazul cel mai defavorabil este O(lg n) (sau mai bun). Daca totusi un heap binar trebuie sa execute operatia REUNEsTE, aceasta va fi lenta. Prin concatenarea celor doua tablouri care memoreaza heap-urile binare care se interclaseaza si apoi aplicarea operatiei RECONSTITUIE-HEAP, timpul de executie, în cazul cel mai defavorabil, pentru operatia REUNEsTE este q(n).
|
procedura |
heap binar (cazul cel mai defavorabil) |
heap binomial (cazul cel mai defavorabil) |
heap Fibonacci (amortizat) |
|
CREEAZĂ-HEAP |
q |
q |
q |
|
INSEREAZĂ |
q(lg n) |
O(lg n) |
q |
|
MINIMUM |
q |
O(lg n) |
q |
|
EXTRAGE-MIN |
q(lg n) |
q(lg n) |
O(lg n) |
|
REUNEsTE |
q(n) |
O(lg n) |
q |
|
DESCREsTE-CHEIE |
q(lg n) |
q(lg n) |
q |
|
sTERGE |
q(lg n) |
q(lg n) |
O(lg n) |
În tabel sunt prezentati timpii de executie ai operatiilor pentru trei implementari ale heap-urilor interclasabile. Numarul elementelor din heap-urile folosite de o operatie este notat cu n.
În continuare vom analiza heap-urile binomiale a caror margini pentru timpii de executie, în cazurile cele mai defavorabile, sunt prezentate în tabelul de mai sus. În particular, operatia reuneste pentru interclasarea a doua heap-uri binomiale cu n elemente va fi de complexitate O(lg n). Vor fi ignorate operatiile de alocare a nodurilor înainte de o inserare si de eliberare a nodurilor dupa o stergere. Presupunem ca de aceste detalii este responsabil codul care apeleaza operatiile heap-ului.
Heap-urile binare, binomiale si Fibonacci sunt ineficiente în raport cu operatia de CĂUTARE; pentru gasirea unui nod care contine o anumita valoare nu se poate stabili o cale de cautare directa în aceste structuri. Din acest motiv, operatiile DESCREsTE-CHEIE si sTERGE care se refera la un anumit nod reclama ca parametru de intrare un pointer la nodul respectiv. În cele mai multe aplicatii aceasta cerinta nu ridica probleme.
13.3 Arbori binomiali
figura
13.2 Deoarece
un heap binomial este o colectie de arbori binomiali, vom prezenta mai
intâi arborii binomiali si demonstra unele proprietati
esentiale ale acestora. Arborele binomial Bk este un arbore
ordonat definit recursiv. Dupa cum se vede în figura de mai jos, arborele
binomial B0 consta dintr-un singur nod. Arborele binomial
Bk consta din doi arbori binomiali Bk-1 care sunt
înlantuiti: radacina unui dintre ei este fiul situat
cel mai în stânga radacinii celuilalt arbore. Figura prezinta
arborii binomiali de la B0 la B4. 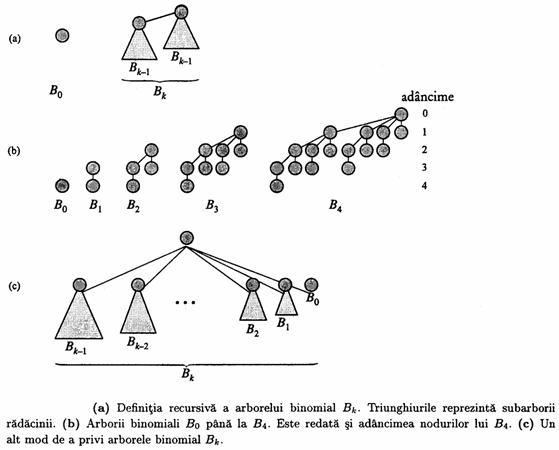
Lema urmatoare contine câteva proprietati ale arborilor binomiali.
Arborele binomial Bk are:
1. 2k noduri,
![]() 2. înaltimea k,
2. înaltimea k,
3. exact noduri, la adâncimea i, pentru i=0,1,.,k.
4. radacina de grad k, grad mai mare decât al oricarui alt nod; mai mult, daca fii radacinii sunt numerotati de la stânga spre dreapta prin k-1, k-2,.,0 atunci fiul i este radacina subarborelui Bi.
Demonstratie
Demonstratia este inductiva în raport cu k. Pasul initial pentru fiecare proprietate îl constituie arborele binomial B0. Verificare prorpietatilor pentru B0 este imediata. Presupunem ca lema are loc pentru arborele Bk-1.
1. Arborele binomial Bk are 2k-1+2k-1=2k noduri, deoarece el consta din doua copii ale arborelui Bk-1.
2. Ţinând cont de modul în care sunt înlantuite cele doua copii ale lui Bk-1 pentru a forma Bk, rezulta ca adâncimea maxima a lui Bk este cu 1 mai mare decât adâncimea maxima a lui Bk-1. Din ipoteza de inductie obtinem valoarea (k-1)+1=k pentru adâncimea maxima a lui Bk.
![]()
3. Fie D(k,i) numarul nodurilor situate pe
nivelurile i al arborelui binomial Bk. Deoarece Bk este
compus din doua copii înlantuite ale lui Bk-1, un nod
de pe nivelul i din Bk-1 apare în Bk pe nivelele i
si i+1. Altfel spus, numarul nodurilor situate pe nivelul i în Bk
este egal cu numarul nodurilor de pe nivelul i din Bk-1 plus
numarul nodurilor de pe nivelul i-1 din Bk-1. Astfel,
4. Singurul nod cu grad mai mare în Bk decât în Bk-1 este radacina, care are cu un fiu mai mult decît în Bk-1. Deoarece radacina lui Bk-1 are gradul k-1, radacina lui Bk are gradul k. Din ipoteza de inductie si dupa cum ilustreaza figura de mai sus, fii lui Bk-1 (de la stânga la dreapta) sunt radacinile arborilor Bk-2, Bk-3, ., B0. Când Bk-1 este legat la Bk-1, fii radacinii rezultate sunt radacini pentru Bk-1, Bk-2, ., B0.
Corolar
Gradul maxim al nodurilor unui arbore binomial având n noduri este lg n.
Demonstratie
![]() Rezulta imediat din prorietatile 1
si 4 ale lemei de mai sus.
Rezulta imediat din prorietatile 1
si 4 ale lemei de mai sus.
Proprietatea 3 a lemei justifica termenul de arbore binomial prin faptul ca sunt coeficientii binomiali.
Heap-uri binomiale
Un heap binomial H este format dintr-o multime de arbori binomiali care satisfac urmatoarele proprietati de tip binomial.
1. Fiecare arbore binomial din H satisface proprietatea de ordonare a unui heap: cheia unui nod este mai mare sau egala decât cheia parintelui sau.
2. Exista cel mult un arbore binomial în H a carui radacina are un grad dat.
Conform primei proprietati, radacina unui arbore cu proprietatea de heap ordonat, contine cea mai mica cheie din arbore.
Proprietatea
a doua implica faptul ca un heap binomial H având n noduri
contine cel mult [lg n]+1 arbori binomiali. Pentru o justificare a acestei
afirmatii se observa ca reprezentarea binara a lui n are
[lg n]+1 biti, fie acestia <b[lg n], b[lg n]-1,.,b0>,
astfel încât ![]() . Din proprietatea 1 a lemei de mai sus rezulta ca
arborele binomial Bi apare în H daca si numai daca
bitul bi=1. Astfel heap-ul H contine cel mult [lg n]+1 arbori
binomiali.
. Din proprietatea 1 a lemei de mai sus rezulta ca
arborele binomial Bi apare în H daca si numai daca
bitul bi=1. Astfel heap-ul H contine cel mult [lg n]+1 arbori
binomiali.
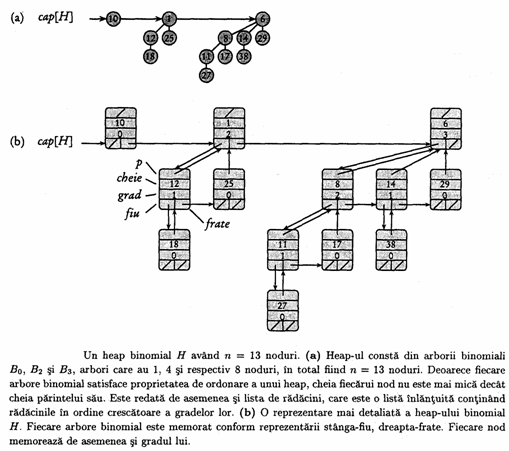
În figura de mai jos este prezentat un heap binomial H având
13 noduri. Reprezeantarea binara a numarului 13 este 1101, iar H
contine arborii binomiali cu proprietatea de heap B3, B2
si B0 având 8, 4 si respectiv un nod, în total fiind 13
noduri.
figura 13.3
Reprezentarea heap-urilor binomiale
Dupa cum ilustreaza si figura de mai sus, fiecarea arbore binomial al unui heap binomial este memorat conform reprezentarii stânga-fiu, dreapta-frate. Fiecare nod are un câmp cheie plus alte informatii specifice aplicatiei care foloseste heap-ul. În plus, fiecare nod x contine pointerii p[x] spre parintele lui, fiu[x] spre fiul situat cel mai în stânga si frate[x] spre fratele lui x, situat imediat în dreapta. Daca nodul x este o radacina atunci p[x]=NIL. Daca nodul x nu are fii atunci fiu[x]=NIL, iar daca x este fiu situat cel mai în dreapta, atunci frate[x]=NIL. Fiecare nod contine de asemenea câmpul grad[x], care reprezinta numarul fiilor lui x.
Rezulta din figura ca radacinile arborilor binomiali continuti de un heap binomial sunt pastrate într-o lista înlantuita pe care o vom numi în continuare lista de radacini. La o traversare a listei de radacini gradul radacinilor formeaza un sir strict crescator. Din a doua proprietate de heap binomial, rezulta ca gradele radacinilor unui heap binomial având n noduri formeaza o submultime a multimii . Câmpul frate are semnificatii diferite dupa cum nodurile sunt radacini sau nu. Daca x este radacina atunci frate[x] refera radacina urmatoare în lista de radacini. (daca x este ultima radacina din lista atunci, ca de obicei, frate[x]=NIL.)
Un heap binomial dat H este referit prin pointerul cap[H] spre prima radacina din lista de radacini a lui H. Daca heap-ul binomial H nu are elemente, atunci cap[H]=NIL.
13.4 Operatii pe heap-uri binomiale
Crearea unui heap binomial nou
Pentru a crea un heap binomial vid, procedura CREEAZĂ-HEAP-BINOMIAL va aloca si returna un obiect H, pentru care cap[H]=NIL. Timpul de executie este q
Gasirea cheii minime
Procedura HEAP-BINOMIAL-MIN returneaza un pointer y la nodul cu cea mai mica cheie dintr-un heap binomial H având n noduri. Aceasta implementare presupune ca nu exista chei cu valoarea
HEAP-BINOMIAL-MIN(H,y)
1: y=NIL
2: x=cap[H]
3: min=
4: cât timp x NIL executa
daca cheie[x]<min atunci
min=cheie[x]
y=x
sfârsit daca
y=frate[x]
10: sfârsit cât timp
11: return
Cheia minima a unui heap binomial se afla într-o radacina deoarece este un heap ordonat. Procedura HEAP-BINOMIAL-MIN verifica toate radacinile (în numar de cel mult [lg n]+1) si retine minimul curent în min, respectiv un pointer la acest minim în y. Apelata pentru heap-ul binomial din figura 3, procedura va returna un pointer la nodul care contine cheia 1.
Timpul de executie al procedurii HEAP-BINOMIAL-MIN este O(lg n) deoarece exista cel mult [lg n]+1 radacini verificate.
Reuniunea a doua heap-uri binomiale
Operatia de reuniune a doua heap-uri binomiale este folosita de aproape toate celelalte operatii ramase. Procedura HEAP-BINOMIAL-REUNEsTE înlantuie repetat arborii binomiali care au radacini de acelasi grad. Procedura urmatoare leaga arborele Bk-1 având nodul radacina y la arborele Bk-1 având nodul radacina z; mai precis, z va fi parintele lui y. Nodul z devine astfel radacina unui arbore Bk.
BINOMIAL-LEGĂTURĂ(y,z)
1: p[y]=z
2: frate[y]=fiu[z]
3: fiu[z]=y
4: grad[z]=grad[z]+1
5: return
Procedura BINOMIAL-LEGĂTURĂ plaseaza nodul y în capul listei înlantuite care contine fiii nodului z într-un timp O(1). Reprezentarea stânga-fiu, dreapta-frate a fiecarui arbore binomial asigura succesul acestei proceduri deoarece fiecare arbore binomial are proprietatea de ordonare a arborelui: fiu cel mai din stânga al radacinii unui arbore Bk este radacina unui arbore Bk-1.
Procedura HEAP-BINOMIAL-REUNEsTE uneste doua heap-uri binomiale H1 si H2 si returneaza heap-ul rezultat. Pe parcursul efectuarii operatiei, reprezentarile heap-urilor H1 si H2 sunt distruse. Procedura foloseste pe lânga procedura BINOMIAL-LEGĂTURĂ înca o procedura auxiliara ANSAMBLU-BINOMIAL-INTERCLASEAZĂ, care interclaseaza listele de radacini ale heap-urilor H1 si H2 într-o singura lista simplu înlantuita ordonata crescator dupa gradul nodurilor.
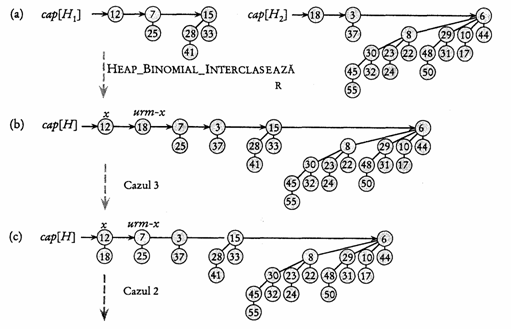
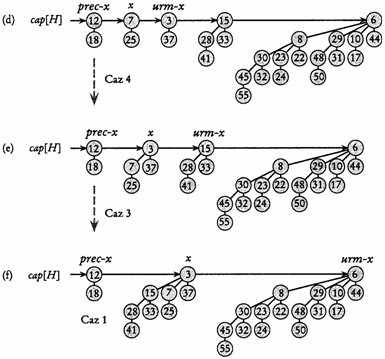

figura 13.4
În figura 13.4 se prezinta un exemplu pentru care se petrec toate cele patru cazuri indicate prin comentarii în procedura HEAP-BINOMIAL-REUNEsTE.
Procedura HEAP-BINOMIAL-REUNEsTE se desfasoara în doua faze. În prima faza se interclaseaza (prin apelul HEAP-BINOMIAL-INTERCLASEAZĂ) listele de radacini ale heap-urilor binomiale H1 si H2 într-o lista simplu înlantuita H care este ordonata crescator în raport cu gradul nodurilor radacina. Lista formata poate contine cel mult doua radacini cu acelasi grad. Astfel, în faza a doua sunt unite toate radacinile care au acelasi grad, astfel încât sa nu existe doua noduri cu acelasi grad. Deoarece lista înlantuita H este ordonata dupa grad, operatiile de înlantuire din faza a doua sunt efectuate rapid.
Detaliem cele doua fraze ale procedurii. Liniile 1-3 încep prin interclasarea celor doua liste ale heap-urilor binomiale H1 si H2 într-o singura lista de radacini H. Listele de radacini ale lui H1 si H2 sunt ordonate strict crescator dupa grad, iar HEAP-BINOMIAL-INTERCLASEAZĂ returneaza o lista de radacini H, ordonata crescator dupa grad. Daca listele H1 si H2 au împreuna m noduri, atunci timpul de executie pentru HEAP-BINOMIAL-INTERCLASEAZĂ este O(m), datorat examinarii repetate a radacinilor din capul listelor si adaugarii radacinii având gradul mai mic în lista de radacini rezultat, eliminând aceasta radacina din lista data la intrare.
HEAP-BINOMIAL-REUNEsTE(H1,H2,H)
1: Cheama CREEAZĂ-HEAP-BINOMIAL(H )
2: Cheama HEAP-BINOMIAL-INTERCLASEAZĂ(H1,H2,H)
3: elibereaza obiectele H1,H2, dar nu si listele referite de ele
4: daca cap[H]=NIL atunci
5: return
6: sfârsit daca
7: prec-x=NIL
8: x=cap[H]
9: urm-x=frate[x]
10: cât timp urm-x NIL
daca (grad[x] grad[urm-x]) sau (frate[urm-x] NIL si grad[frate[urm-x]]=grad[x]) atunci
prec-x=x cazurile 1 si 2
x=urm-x cazurile 1 si 2
altfel
daca cheie[x] cheie[urm-x] atunci
frate[x]=frate[urm-x] cazul 3
BINOMIAL-LEGĂTURĂ(urm-x,x) cazul 3
altfel
daca prec-x=NIL atunci
cap[H]=urm-x cazul 4
altfel
frate[prec-x]=urm-x cazul 4
sfârsit daca
BINOMIAL-LEGĂTURA(x,urm-x) cazul 4
x=urm-x cazul 4
sfârsit daca
urm-x=frate[x] cazul 4
sfârsit daca
28: sfârsit daca
29: sfârsit cât timp
30: return
În continuare procedura HEAP-BINOMIAL-REUNEsTE initializeaza câtiva pointeri în lista de radacini H. Daca heap-urile binomiale date la intrare sunt vide, atunci în liniile 4-5 se iese din procedura. Începând cu linia 6 ne situam în cazul în care H contine cel putin o radacina. Din acest punct se pastreaza 3 pointeri în lista de radacini:
- x indica radacina curenta examinata,
- prec-x indica radacina precedenta lui x în lista de radacini: frate[prec-x]=x,
- urm-x indica radacina urmatoare lui x în lista: frate[x]=urm-x.
H poate contine initial cel mult doua radacini cu un grad dat: deoarece H1 si H2 sunt heap-uri binomiale, ele nu au doua radacini având acelasi grad. Mai mult, procedura HEAP-BINOMIAL-INTERCLASEAZĂ ne garanteaza ca daca H contine doua radacini având acelasi grad, atunci ele sunt adiacente în lista de radacini.
În timpul executiei procedurii HEAP-BINOMIAL-REUNEsTE, de fapt, pot exista 3 radacini având acelasi grad. Vom vedea când se produce aceasta situatie. La fiecare iteratie a ciclului cât timp din liniile 9-24 se decide daca se poate lega x si urm-x în functie de gradul lor si de gradul lui frate[urm-x]. Un invariant al acestui ciclu este faptul ca la fiecare reluare a corpului ciclului atât x cât si urm-x sunt diferiti de NIL.
figura
13.5
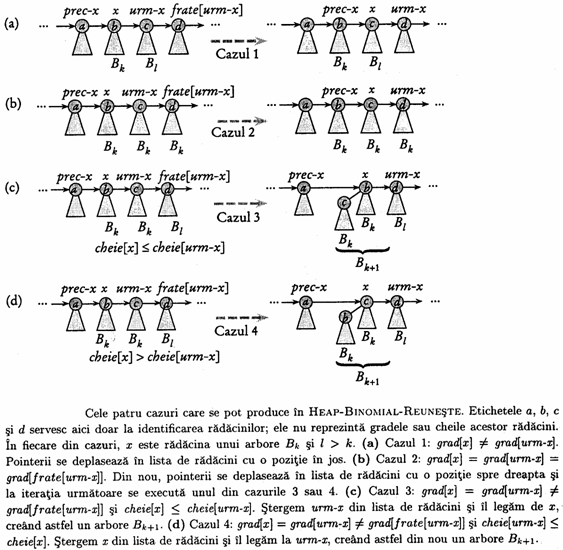
Cazul 1, prezentat în figura 13.5.a se produce atunci când grad[x] grad[urm-x], adica x este radacina unui arbore Bk si urm-x este radacina unui arbore Bl pentru un l>k. Aceasta situatie este tratata în liniile 11-12. Deoarece nu trebuie sa legam x si urm-x, nu ramâne decât sa deplasam pointerii în lista. Actualizarea pointerului urm-x pentru a referi nodul ce urmeaza noului nod x este efectuata în linia 24, deoarece aceasta este comuna tuturor cazurilor.
Cazul 2, prezentat în figura 13.5.b, are loc atunci când x este prima radacina din cele 3 care au acelasi grad, adica atunci când grad[x]=grad[urm-x]=grad[frate[urm-x]]
Acest caz este tratat similar cu cazul 1: efectuam doar o deplasare a pointerilor în lista. Testul din linia 10 este comun cazurilor 1 si 2, la fel cum liniile 11-12 trateaza amândoua cazurile.
Cazurile 3 si 4 se produc atunci când x este prima radacina din 2 radacini succesive având acelasi grad, adica grad[x]=grad[urm-x] grad[frate[urm-x]].
Aceste cazuri apar la iteratia urmatoare dupa fiecare caz, dar unul din ele urmeaza imediat dupa cazul 2. În cazurile 3 si 4 vom înlantui x si urm-x. Aceste cazuri difera între ele dupa cum x sau urm-x au cheia mai mica, fapt ce determina care din noduri va fi radacina în procesul de legare a lor.
În cazul 3, prezentat în figura 13.5.c, cheie[x] cheie[urm-x], astfel ca urm-x va fi legat la linia x. Linia 15 sterge urm-x din lista de radacini, iar în linia 16 urm-x devine fiul situat cel mai în stânga lui x.
În cazul 4, prezentat în figura 13.5.d cheia mai mica o are urm-x, deci este legat la urm-x. Liniile 17-21 sterg x din lista de radacini. Exista doua subcazuri, dupa cum x este (linia 19) sau nu (linia 21) prima radacina din lista. În linia 22, x devine fiul situat cel mai în stânga lui urm-x, iar linia 23 actualizeaza x pentru iteratia urmatoare.
Pregatirea iteratiei urmatoare a ciclului cât timp este aceeasi pentru ambele cazuri 3 si 4. x refera un arbore Bk+1 obtinut prin negarea a doi arbori Bk. Dupa operatia HEAP-BINOMIAL-INTERCLASEAZĂ în lista de radacini existau zero, unu sau doi arbori Bk+1, deci x este acum prima radacina din lista de radacini pentru un numar de unu, doi sau trei arbori Bk+1. În cazul existentei unui singur arbore (x referindu-l pe acesta), la iteratia urmatoare se va produce cazul 1: grad[x] grad[urm-x]. Daca x refera primul arbore din doi existenti atunci la iteratia urmatoare are loc unul din cazurile 3 sau 4. În sfârsit, daca x refera primul arbore din trei existenti atunci la iteratia urmatoare are loc cazul 2.
Timpul de executie pentru HEAP-BINOMIAL-REUNEsTE este O(lg n), unde n este numarul total de noduri din heap-urile binomiale H1 si H2. Justificam acest rezultat dupa cum urmeaza: fie n1 si n2 numarul nodurilor heap-urilor H1 si respectiv H2 astfel încât n=n1+n2. Atunci numarul maxim de radacini continute de H1 si H2 este [lg n1]+1, respectiv [lg n2]+1. Astfel imediat dupa apelul HEAP-BINOMIAL-INTERCLASEAZĂ, H contine cel mult [lg n1]+[lg n2]+2 2[lg n]+2=O(lg n) radacini. Rezulta ca timpul de executie pentru HEAP-BINOMIAL-INTERCLASEAZĂ este O(lg n). Fiecare iteratie a ciclului cât timp se executa într-un timp O(1) si pot exista cel mult [lg n1]+[lg n2]+2 iteratii deoarece de la fiecare iteratie fie pointerii avanseaza cu o pozitie în lista H, fie se elimina o radacina din lista de radacini. Astfel, timpul total de executie este O(lg n).
Inserarea unui nod
Procedura urmatoare insereaza nodul x în heap-ul binomial H. Se presupune ca nodul x este creat si câmpul cheie[x] este initializat.
HEAP-BINOMIAL-INSEREAZĂ(H,x)
1: Cheama CREEAZĂ-HEAP-BINOMIAL(H' )
2: p[x]=NIL
3: fiu[x]=NIL
4: frate[x]=NIL
5: grad[x]=0
6: cap[H']=x
7:Cheama HEAP-BINOMIAL-REUNEsTE(H,H',H)
8: return
Procedura creeaza un heap binomial H' cu un nod într-un timp O(1) pe care îl reuneste apoi cu heap-ul binomial H având n noduri într-un timp O(lg n). Procedura HEAP-BINOMIAL-REUNEsTE elibereaza spatiul alocat heap-ului binomial temporar H'.
Extragerea nodului având cheia minima
Procedura urmatoare extrage nodul având cheia minima din heap-ul binomial H si returneaza un pointer la nodul extras.
HEAP-BINOMIAL-EXTRAGE-MIN(H)
1: cauta radacina x cu cheia minima în lista de radacini si sterge x din lista de radacini a lui H
2: Cheama CREEAZĂ-HEAP-BINOMIAL(H')
3: inverseaza ordinea memorarii fiilor lui x în lista înlantuita asociata si atribuie lui cap[H'] capul listei rezultate
4: Cheama HEAP-BINOMIAL-REUNEsTE(H,H',H)
5: returne
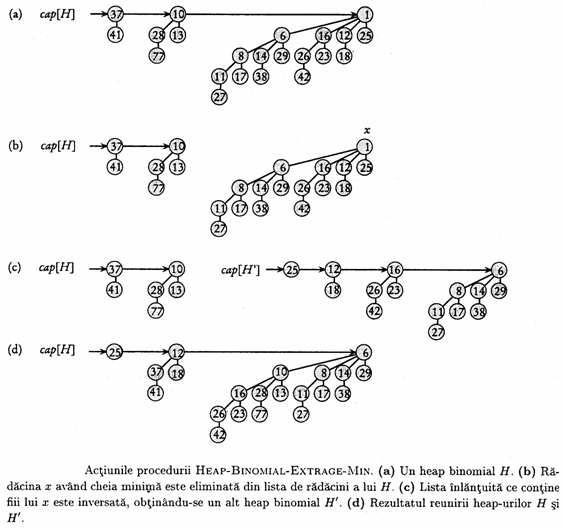
figura 13.6
Modul de functionare al procedurii este ilustrat în figura 13.6. Heap-ul binomial H dat ca parametru de intrare este ilustrat în figura 13.6.a. Figura 13.6.b prezinta situatia obtinuta dupa linia 1: radacina x având cheia minima a fost eliminata din lista de radacini a lui H. Daca x este radacina unui arbore Bk, atunci fiii lui x de la stânga la dreapta, sunt radacinile unor arbori Bk-1, Bk-2,., B0. În figura 6.c se ilustreaza faptul ca inversând lista fiilor lui x (în linia 3) obtinem un heap binomial H' care contine toate nodurile din arborele corespunzator lui x, exceptându-l pe x. Deoarece în linia 1 arborele lui x este sters din H, heap-ul binomial rezultat prin reunirea în linia 4 a lui H si H', conform figurii 6.d, va contine toate nodurile care existau initial în H, exceptându-l desigur pe x. În final, în linia 5 se returneaza x.
HEAP-BINOMIAL-EXTRAGE-MIN se executa într-un timp O(lg n) deoarece fiecare din liniile 1-4 se executa într-un timp O(lg n).
Descresterea unei chei
Procedura HEAP-BINOMIAL-DESCREsTE-CHEIE(H,x,k)
1: daca k>cheie[x] atunci
2: eroare "cheia noua este mai mare decât cheia existenta"
3: sfârsit daca
4: cheie[x]=k
5: y=x
6: z=p[y]
7: cât timp z NIL si cheie[y]<cheie[z]
8: interschimba cheie[y] cheie[z]
9: daca y si z au si alte câmpuri atunci interschimba si aceste câmpuri
10: y=z
11: z=p[y]
12: sfârsit cât timp
figura
13.7
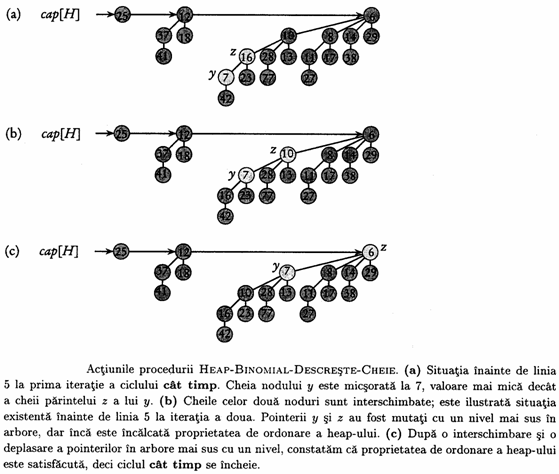
Aceasta procedura descreste o cheie în mod similar cu metoda aplicata pentru un heap binar: prin "ridicarea" cheii în heap, dupa cum arata figura 7. Dupa ce procedura se asigura ca noua cheie nu este mai mare decât cea curenta si apoi actualizeaza cheia curenta a lui x, urmeaza un proces de cautare în sus, iar y refera initial nodul x. La fiecare iteratie a ciclului cât timp, în liniile 6-10, se compara cheie[y] cu cheia parintelui z a lui y.Daca y este chiar radacina sau cheie[y] cheie[z], atunci arborele binomial este un heap ordonat. În caz contrar nodul y încalca proprietatea de ordonare pentru heap, astfel cheile lui y si z se interschimba, împreuna cu alte informatii, apoi procedura deplaseaza y si z cu un nivel mai sus în arbore si continua iteratiile.
Timpul de executie HEAP-BINOMIAL-DESCREsTE-CHEIE este O(lg n). Numarul maxim de iteratii pentru ciclul cât timp (liniile 6-10) este [lg n] deoarece, din proprietatea 2 a lemei enuntate mai sus rezulta ca înaltimea maxima a lui x este [lg n].
stergerea unei chei
stergerea cheii si a altor informatii asociate unui nod x apartinând unui heap binomial H se poate desfasura fara dificultate într-un timp O(lg n). Implementarea urmatoare presupune ca nodurile din heap-ul binomial nu au chei având valoarea -
HEAP-BINOMIAL-sTERGE(H,x)
1: HEAP-BINOMIAL-DESCREsTE-CHEIE(H,x,-
2: HEAP-BINOMIAL-EXTRAGE-MIN(H)
Dupa ce în procedura HEAP-BINOMIAL-sTERGE se atribuie valoarea - cheii nodului x, acesta devine nodul având cheia minima în heap-ul binomial. Urmeaza apoi ca aceasta cheie si eventual alte informatii asociate sa fie ridicate pâna la o radacina prin apelul HEAP-BINOMIAL-DESCREsTE-CHEIE. Aceasta radacina este apoi eliminata din H prin apelul HEAP-BINOMIAL-EXTRAGE-MIN.
Timpul de executie pentru HEAP-BINOMIAL-sTERGE este O(lg n).
13.3 Heap-uri Fibonacci
Un arbore cu radacina este un arbore liber în care unul dintre vârfuri se deosebeste de celelalte. Vârful evidentiat se numeste radacina arborelui.
Un arbore ordonat este un arbore cu radacina în care fiii fiecarui nod sunt ordonati. Cu alte cuvinte, daca un nod are k fii, atunci exista un prim fiu, un al doilea fiu,.si un al k - lea fiu.
Arborele binomial Bk este un arbore ordonat definit recursiv:
arborele binomial B0 consta dintr-un singur nod;
2. arborele binomial Bk consta din doi arbori binomiali Bk-1 care sunt înlantuiti: radacina unuia dintre ei este fiul situat cel mai în stânga radacinii celuilalt arbore.
Un heap binomial H este format dintr-o multime de arbori binomiali care satisfac urmatoarele proprietati de heap binomial :
fiecare arbore binomial din H satisface proprietatea de ordonare a unui heap : cheia unui nod este mai mare sau egala decât cheia parintelui sau;
exista cel mult un arbore binomial în H a carui radacina are un grad dat.
Conform acestei definitii, radacina unui arbore cu proprietatea de heap ordonat, contine cea mai mica cheie din arbore.
Similar cu un heap binomial, un heap Fibonacci este o colectie de arbori care au proprietatea de ordonare de heap. Totusi, arborii dintr-un heap Fibonacci nu trebuie sa fie arbori binomiali. Figura 13.8(a) reprezinta un exemplu de heap Fibonacci.
Spre deosebire de arborii dintr-un heap binomial, care sunt ordonati, arborii apartinând unui heap Fibonacci sunt arbori cu radacina , dar neordonati. Dupa cum prezinta figura 13.8(b), fiecare nod x contine un pointer p[x] spre parintele lui si un pointer fiu[x] la unul din fiii lui. Fiii lui x sunt înlantuiti circular printr-o lista dublu înlantuita, numita lista fiilor lui x. Fiecare fiu y dintr-o lista de fii are pointerii stânga[y] si dreapta[y] care indica fratele stâng, respectiv drept al lui y. Daca nodul y este singurul fiu, atunci stânga[y] = dreapta[y] =y . Ordinea în care apar fiii în lista este arbitrara.
Folosirea listelor dublu înlantuite si circulare pentru heap-uri Fibonacci are doua avantaje. În primul rând, putem sterge un nod dintr-o lista dublu înlantuita si circulara într-un timp O(1). În al doilea rând, putem concatena doua liste de acest tip, obtinând o singura lista dublu înlantuita si circulara tot într-un timp O(1). În descrierea operatiilor pe heap-uri Fibonacci ne vom referi informal la aceste operatii pe liste.
Fiecare nod va contine înca doua câmpuri utile. Numarul de fii din lista fiilor nodului x este memorat în grad[x]. Câmpul de tip boolean marcat[x] va indica daca nodul x a pierdut un fiu dupa ultima operatie în care x a fost transformat în fiul unui alt nod. Nodurile nou create nu sunt marcate, iar un nod x devine nemarcat atunci când este transformat în fiul unui alt nod.
Un heap Fibonacci H este referit printr-un pointer min[H] al radacinii arborelui care contine cheia minima; acest nod este numit nodul minim al heap-ului Fibonacci. Daca un heap Fibonacci este vid, atunci min[H] =NIL
Radacinile tuturor arborilor dintr-un heap Fibonacci sunt înlantuite prin pointerii stânga si dreapta, formând o lista dublu înlantuita si circulara, numita lista de radacini a heap-ului Fibonacci. Astfel, pointerul min [H] indica acel nod din lista de radacini care are cheia minima. Ordinea nodurilor din lista de radacini este arbitrara. Un atribut pe care ne vom baza este si numarul nodurilor n[H] al unui heap Fibonacci H.
13.4 Metoda de potential
Vom folosi în analiza complexitatii operatiilor pe heap-uri Fibonacci metoda de potential .
Descriem în continuare cum lucreaza metoda de potential. Plecam de la o structura de date initiala D0 asupra careia se executa n operatii. Pentru fiecare i=1,2,.,n, fie ci costul real al operatiei i si fie Di structura de date obtinuta din Di-1 dupa aplicarea operatiei i. O functie de potential Ф ataseaza fiecarei structuri de date Di numarul Ф(Di ), care este potentialul asociat structurii de date Di . Costul amortizat i al operatiei i pentru functia de potential Ф este definit astfel:
i = ci + Ф(Di) - Ф(Di-
Prin urmare, costul amortizat al fiecarei operatii este costul real plus cresterea de potential datorata operatiei.
Conform ecuatiei (13.1), costul amortizat total al celor n operatii este:
n n n
i = (ci + Ф(Di) - Ф(Di- ci + Ф(Dn) - Ф(D0) (13.2)
i=1 i=1 i=1
Costurile amortizate definite de ecuatiile (13.1) si (13.2) depind de alegerea functiei de potential Ф. Functii de potential diferite pot conduce la costuri amortizate diferite, care ramân însa margini superioare ale costurilor reale. De multe ori are loc o "negociere" la alegerea functiei de potential: cea mai buna functie de potential depinde de limitele de timp dorite.
Pentru un heap Fibonacci H vom indica prin t(H) numarul radacinilor din lista de radacini a lui H, iar prin m(H) numarul nodurilor marcate din H. Potentialul unui heap Fibonacci este definit prin:
Ф(H)=t(H)+2m(H) (13.3)
De exemplu,
potentialul heap-ului Fibonacci din figura 13.8 este 5+2·3=11.
Potentialul unei multimi de heap-uri Fibonacci este egal cu suma
potentialelor heap-urilor Fibonacci continute. Vom presupune ca
o unitate de potential corespunde unui volum de calcul constant, cu o
(a) min[H]
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() ------ -------- ----- ----- ------ ----- ----- ----------
----- ----- ----------------
------ -------- ----- ----- ------ ----- ----- ----------
----- ----- ----------------
(b). min[H]
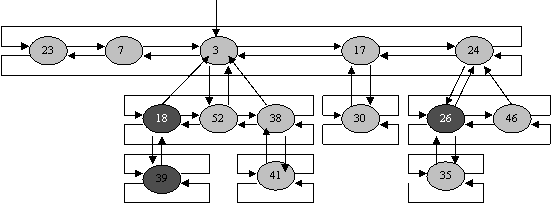
Figura Heap Fibonacci
(a) Un heap Fibonacci constând din 5 arbori , ce satisfac proprietatea de heap ordonat, si care contine 14 noduri . Linia punctata indica lista de radacini. Nodul care contine valoarea 3 este nodul minim din heap. Nodurile marcate sunt hasurate cu negru. Potentialul acestui heap Fibonacci este 5 + 2·3 =11.
(b) O reprezentare mai complexa care arata pointerii p (sagetile orientate în sus), fiu (sagetile în jos), si stâng (sagetile laterale). Aceste detalii vor fi omise în celelalte figuri deoarece toate informatiile prezentate aici pot fi determinate din ceea ce apare în partea (a).
Vom presupune ca aplicatiile pentru heap-uri Fibonacci nu pornesc de la nici un heap. Astfel, potentialul initial este 0 si conform ecuatiei (1.2.3) , potentialul este nenegativ la orice moment de timp ulterior. O margine superioara a costului amortizat total este si o margine superioara a costului actual pentru secventa de operatii.
Grad maxim
În sectiunea urmatoarea vom efectua o analiza amortizata care se va baza pe cunoasterea unei margini superioare D(n) a gradului maxim al oricarui nod dintr-un arbore Fibonacci având n noduri. Atunci când avem doar operatii de interclasare pe heap-uri D(n)= [lg n]. În sectiunea 1.3 vom arata ca, daca includem si operatiile DESCREsTE-CHEIE si sTERGE, D(n) =O(lg n).
13.5 Operatii cu heap-uri interclasabile
În aceasta sectiune vom descrie si analiza operatiile heap-urilor interclasabile precum si implementari pe heap-uri Fibonacci. Daca se au în vedere doar aceste operatii - CREAZĂ-HEAP, ÎNSEREAZĂ, MINIM, EXTRAGE-MIN, REUNEsTE - fiecare heap Fibonacci este o colectie de arbori binomiali "neordonati". Un arbore binomial neordonat este asemanator unui arbore binomial si se defineste , de asemenea, recursiv. Arborele binomial neordonat Uk consta dintr-un singur nod, iar un arbore binomial neordonat Uk consta din doi arbori binomiali neordonati Uk-1, radacina unuia din ei fiind (oricare) fiu al radacinii celuilalt. Astfel, avem urmatoarea lema care contine propietati pentru arborii binomiali neordonati:
Lema 13.1 Arborele binomial Uk are:
2k noduri,
înaltimea k,
k i
exact ), noduri , la adâncimea i , pentru i = 0,1 ,...,k,
gradul radacinii arborelui binomial Uk este k, grad mai mare decât al oricarui alt nod. Într-o ordine oarecare, descendentii radacinii sunt radacinile unor arbori U ,U Uk-1.
Astfel, deoarece un heap Fibonacci având n noduri este o colectie de arbori binomiali neordonati, D(n) = lg n..
Ideea de baza , aplicata la definirea operatiilor heap-urilor interclasabile pe heap-uri Fibonacci este de a întârzia anumite prelucrari cât mai mult posibil. Obtinerea unor operatii performante poate fi în detrimentul altora. Daca numarul arborilor unui heap Fibonacci este mic, atunci nodul minim necesar operatiei EXTRAGE-MIN este determinat eficient. Dar, dupa cum se stie pentru heap-uri binomiale, costul asigurarii unui numar mic de arbori este ridicat: pentru inserarea unui nod într-un heap binomial, sau pentru reuniunea a doua heap-uri binomiale , timpul de executie se poate ridica pâna la Ώ(lg n). Dupa cum se va vedea, la inserarea unui nod nou sau la reuniunea a doua heap-uri , nu vom încerca sa consolidam arborii din heap-ul Fibonacci. Consolidarea va fi lasata în seama operatiei EXTRAGE-MIN, operatie care necesita gasirea nodului minim.
13.5.1 Crearea unui heap Fibonacci
Pentru a crea un heap Fibonacci vid , procedura HEAP-FIB-CREAZĂ, creeaza si returneaza un obiect heap Fibonacci H, cu n[H] = 0 si min[H] = NIL; H nu contine arbori. Deoarece t(H) = 0 si m(H) = 0, potentialul heap-ului Fibonacci vid este (H) = 0. Costul amortizat al operatiei HEAP-FIB-CREAZĂ este egal cu costul ei actual O(1).
13.5.2 Inserarea unui nod
Procedura urmatoare insereaza nodul x în heap-ul Fibonacci H, presupunând ca nodul a fost alocat în prealabil si ca cheie[x] a fost de asemenea initializata.
HEAP-FIB-INSEREAZĂ (H,x)
grad[x] = 0
p[x] = NIL
fiu[x] = NIL
stânga[x] = x
dreapta[x] = x
marcat[x] = FALS
concateneaza lista de radacini care îl contine pe x cu lista de radacini a lui H
daca min[H] = NIL sau cheie[x] < cheie[min[H]] atunci
min[H] = x
Sdaca
n[H] = n[H]
12. return
Dupa initializarea câmpurilor nodului x în liniile 1-6 , facându-l circular si dublu înlantuit, în linia 7, x este adaugat listei de radacini a lui H într-un timp actual O(1). Astfel, nodul x devine un arbore cu un singur nod si care are proprietatea de ordonare de heap, deci un arbore binomial neordonat apartinând heap-ului Fibonacci. Acest arbore nu are fii si nu este marcat. În continuare, în liniile 8-10, este actualizat, daca este necesar, pointerul la nodul minim din heap-ul Fibonacci H. În final, linia 11 incrementeaza n[H] marcând inserarea unui nod nou. Figura 13.9 prezinta inserarea nodului având cheia 21 în heap-ul Fibonacci din figura 13.8.
(a) min[H]
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() ------ -------- ----- ----- ------ ----- ----- ----------
----- ----- ----------------
------ -------- ----- ----- ------ ----- ----- ----------
----- ----- ----------------
(b) min[H]
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() -------- ----- ------ -------- ----- ------ ----- ----- --------------
-------- ----- ------ -------- ----- ------ ----- ----- --------------
Figura 13.9 Inserarea unui nod într-un heap Fibonacci.
a) Un heap Fibonacci H.
b) Heap-ul Fibonacci H dupa ce nodul având cheia 21 a fost inserat. Nodul devine un arbore cu proprietatea de heap si adaugat listei de radacini, devenind fratele stâng al radacinii.
Procedura HEAP-FIB-INSEREAZĂ nu consolideaza arborii din heap-ul Fibonacci. Daca procedura HEAP-FIB-INSEREAZĂ este apelata consecutiv de k ori atunci se adauga listei de radacini k arbori cu un singur nod.
Pentru a determina costul amortizat al operatiei HEAP-FIB-INSEREAZĂ, fie H heap-ul Fibonacci dat ca intrare si H' heap-ul Fibonacci rezultat. Atunci :
t (H') = t (H) +1
m (H') = m (H)
si cresterea potentialului este:
((t (H) + 1) + 2m (H)) - (t (H) + 2m (H)) = 1.
Deoarece costul actual este O(1), costul amortizat este O(1) +1 = O(1).
13.5.3 Gasirea nodului minim
Nodul minim al unui heap Fibonacci H este dat de pointerul min (H), de unde costul actual al operatiei este O(1). Deoarece potentialul lui H nu se schimba, costul amortizat al operatiei este egal cu costul ei actual O(1).
13.5.4 Reuniunea a doua heap-uri Fibonacci
Procedura urmatoare reuneste heap-urile Fibonacci H1 si H2, distrugând H1 si H2 în timpul desfasurarii procesului.
HEAP-FIB-REUNEsTE (H1,H2,H)
Cheama HEAP-FIB-CREAZĂ(H)
min[H] = min[H1]
concateneaza lista de radacini a lui H1 cu lista de radacini a lui H2
daca (min[H1] = NIL ) sau (min [H2] ≠ NIL si min[H2] < min[H2]) atunci
min[H] = min[H2]
Sdaca
n[H] = n[H1] + n[H2]
elibereaza obiectele H1 si H2
return
Liniile 1-3 concateneaza listele de radacini ale lui H1 si H2 obtinându-se o lista de radacini noua H . Liniile 4 si 6 stabilesc nodul minim al lui H, iar linia 7 initializeaza n[H] cu numarul total de noduri. Obiectele H1 si H2 sunt dealocate în linia 8, iar linia 9 returneaza heap-ul Fibonacci H rezultat. Arborii heap-ului nu sunt consolidati, la fel ca si în procedura HEAP-FIB-INSEREAZĂ. Potentialul ramâne neschimbat si anume:
Φ(H) - ( (H1) + (H2)) =
= (t(H) + 2m(H)) - ((t(H1) + 2m(H1)) +((t(H2) + 2m(H2))) = 0,
deoarece t(H) = t(H1) + t(H2) si m(H) = m(H1) + m(H2). Costul amortizat al operatiei HEAP-FIB-REUNEsTE este astfel egal cu costul actual O(1) .
13.5.5 Extragerea nodului minim
Procesul de extragere al nodului minim este cel mai complicat dintre toate operatiile prezentate în aceasta sectiune. Consolidarea arborilor din lista de radacini este efectuata în cadrul acestei operatii. Urmatorul algoritm extrage nodul minim. Algoritmul presupune ca atunci când se sterge un nod dintr-o lista înlantuita, pointerii ramasi în lista sunt actualizati, dar pointerii din nodul eliminat sunt lasati neschimbati. În algoritm se foloseste o procedura auxiliara CONSOLIDEAZĂ care va fi prezentata în continuare.
HEAP-FIB-EXTRAGE-MIN (H,z)
z = min[H]
daca z ≠ NIL atunci
pentru fiecare fiu al lui z
adauga x la lista de radacini a lui H
p[x] = NIL
Spentru
sterge z din lista de radacini a lui H
daca z = dreapta [z]
atunci
min [H] = NIL
altfel
min [H] = dreapta [z]
CONSOLIDEAZĂ(H)
Sdaca
n[H] = n[H] -1
Sdaca
returne
Conform figurii 13.10, procedura HEAP-FIB-EXTRAGE-MIN rupe legaturile între nodul radacina minim respectiv fiii sai si sterge nodul minim din lista de radacini. Apoi consolideaza lista de radacini prin înlantuirea radacinilor de acelasi grad, pâna când ramâne cel mult o radacina de fiecare grad .
Pornim în linia 1 prin retinerea unui pointer z la nodul minim ; în final se va returna acest pointer. Daca z = NIL atunci heap-ul Fibonacci H este vid si prelucrarea este încheiata. În caz contrar, nodul z este sters din H în liniile 3-6 prin transformarea fiilor lui z în radacini si stergerea lui z din lista de radacini (linia 7). Daca z = dreapta [z] atunci z fusese singurul nod din lista de radacini si nu avusese nici un fiu, astfel încât, mai întâi, trebuie sa facem heap-ul H vid. În caz contrar, stabilim pointerul min[H] în lista de radacini astfel încât sa indice nodul minim ramas ( în acest caz, dreapta[z]) diferit de z . Figura 13.10 (b) prezinta heap-ul Fibonacci din figura 13.10 (a) dupa executarea instructiunii din linia 12.
(a) min[H]
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() -------- ----- ------ -------- ----- ------ ----- ----- --------------
-------- ----- ------ -------- ----- ------ ----- ----- --------------
(b) min[H]
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() -------- ----- ------ -------- ----- ------ ----- ----- --------------
-------- ----- ------ -------- ----- ------ ----- ----- --------------
![]()
![]()
(c) 0 1 2 3
![]()
![]()
![]()
![]()
![]() A
A
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() w,x
w,x
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() -------- ----- ------ -------- ----- ------ ----- ----- --------------
-------- ----- ------ -------- ----- ------ ----- ----- --------------
![]()
![]()
(d) 0 1 2 3
![]()
![]()
![]()
![]()
![]()
![]() A
A
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() w,x
w,x
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() -------- ----- ------ -------- ----- ------ ----- ----- --------------
-------- ----- ------ -------- ----- ------ ----- ----- --------------
![]()
![]()
(e) 0 1 2 3
![]()
![]()
![]()
![]()
![]()
![]()
![]() A
A
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() w,x
w,x
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() -------- ----- ------ -------- ----- ------ ----- ----- --------------
-------- ----- ------ -------- ----- ------ ----- ----- --------------
![]()
![]()
(f) 0 1 2 3
![]()
![]()
![]()
![]()
![]()
![]() A
A
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() x
x
![]()
![]()
![]()
![]()
![]()
![]() w
w
(g) 0 1 2 3
![]()
![]()
![]()
![]()
![]() A
A
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() x
x
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() w w
w w
![]()
(h) 0 1 2 3
![]()
![]()
![]()
![]()
![]() A
A
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() x
x
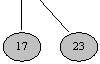
![]()
![]()
![]() w
w
![]()
(i) 0 1 2 3
![]()
![]()
![]()
![]()
![]()
![]() A
A
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() w,x
w,x
![]()
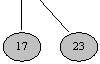
![]()
![]()
![]()

![]()
0 1 2 3 (j)
![]()
![]()
![]()
![]()
![]()
![]()
![]() A
A
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() w,x
w,x
![]()
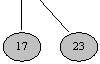
![]()
![]()
![]()

![]()
0 1 2 3 (k)
![]()
![]()
![]()
![]()
![]()
![]() A
A

![]()
![]() w,x
w,x
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()

![]()
![]()
![]()
![]()
![]()
![]()
0 1 2 3 (l)
![]()
![]()
![]()
![]()
![]()
![]()
![]() A
A

![]()
![]() w,x
w,x
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() (m) min [H]
(m) min [H]
![]()
![]()
![]()
![]()

![]()
![]()
![]()
![]()
![]()
![]()
![]()
Figura 13.10 Inserarea unui nod într-un heap Fibonacci.
(a) Un heap Fibonacci H.
(b) Situatia obtinuta dupa stergerea nodului minim z din lista de radacini si adaugarea la lista de radacini a fiilor lui z.
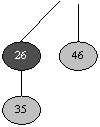
(c)-(e) Tabloul A si arborii dupa primele 3 iteratii ale ciclului pentru din liniile 4-17 ale procedurii CONSOLIDEAZĂ. Lista de radacini este procesata pornind de la nodul minim si urmând pointerii dreapta. Fiecare parte arata valorile lui w si x la sfârsitul unei iteratii.
(f)-(h) Iteratia urmatoare a ciclului pentru , cu valorile lui w si x obtinute la sfârsitul fiecarei iteratii a ciclului cât timp din liniile 7-15 . Partea (f) arata situatia obtinuta la prima trecere prin ciclul cât timp. Nodul cu cheia 23 a fost legat la nodul având cheia 7, nod care este acum indicat de x. În partea (g) , nodul având cheia 17 a fost legat la nodul având cheia 7, spre care înca indica x . În partea (h) , nodul având cheia 24 a fost legat la nodul având cheia 7. Deoarece A[3] nu indica nici un nod, la sfârsitul iteratiei ciclului pentru A[3] va indica radacina arborelui rezultat.
(i)-(l) Situatiile obtinute dupa urmatoarele patru iteratii ale ciclului cât timp.
(m) Heap-ul Fibonacci H dupa reconstruirea listei de radacini din tabloul A si dupa determinarea pointerului min[H].
Pasul urmator în care reducem numarul de arbori din heap-ul Fibonacci consta în consolidarea listei de radacini a lui H; acesta este efectuat prin apelul CONSOLIDEAZĂ(H). Consolidarea listei de radacini consta din efectuarea repetata a pasilor urmatori, pâna când fiecare radacina din lista de radacini are o valoare distincta pentru gradul sau :
Gaseste doua radacini x si y din lista de radacini având acelasi grad si cheie[x] < cheie[y]
Înlantuie y la x sterge y din lista de radacini si include nodul y printre fiii lui x. Aceasta operatie este efectuata prin procedura HEAP-FIB-ÎNLĂNŢUIE. Câmpul grad[x] este incrementat, iar marcajul nodului y, daca exista, este sters.
CONSOLIDEAZĂ(H)
pentru i 0 , D(n(H))
A[i] NIL
Spentru
pentru fiecare nod w din lista de radacini a lui H
x w
d grad[x]
cât timp A[d] NIL
y A[d]
daca cheie[x] > cheie[y] atunci
interschimba x y
Sdaca
HEAP-FIB-ÎNLĂNŢUIE(H,y,x)
A[d] NIL
d d+1
Sciclu
A[d] x
Spentru
min[H] NIL
pentru i 0, D(n[H])
daca A[I] NIL sau cheie[A[i]] < cheie[min[H]] atunci
adauga A[i] listei de radacini a lui H
daca min[H] = NIL sau cheie[A[i]] < cheie[min[H]] atunci
min[H] A[i]
Sdaca
Sdaca
Spentru
return
HEAP-FIB-ÎNLĂNŢUIE (H,y,x)
sterge y din lista de radacini a lui H
înlantuie y ca fiu al lui x si incrementeaza grad[x]
marcat[y] = FALS
return
Procedura CONSOLIDEAZĂ foloseste un tablou auxiliar A[0..D(n[H])]; daca A[i] =y atunci y este o radacina cu grad[y] =i. Aceasta functioneaza dupa cum urmeaza. În liniile 1 - 2 se initializeaza A atribuind fiecarui element valoarea NIL. Procesarea fiecarui nod w se încheie cu un nod x care poate fi , sau nu, identic cu w. Astfel, elementele tabloului A[grad[x]] sunt initializate cu x. În ciclul pentru din liniile 4-17 este examinat fiecare nod w din lista de radacini. Invariantul la fiecare iteratie în ciclul for este ca nodul x este radacina arborelui care contine nodul w.
Ciclul cât timp din liniile 7-15 are predicatul invariant d = grad[x] (cu exceptia liniei 13 dupa cum vom vedea imediat). La fiecare iteratie a ciclului cât timp A[d] indica o anumita radacina y. Deoarece d =grad[x]= grad[y], vom înlantui x si y. Cel care are cheia mai mica dintre x si y devine parintele celuilalt, în urma operatiei de înlantuire; astfel, daca este necesar, pointerii x si y sunt interschimbati în liniile 9-11. În continuare y este legat la x prin apelul din linia 12, HEAP-FIB-ÎNLĂNŢUIE(H,y,x). În urma apelului , grad[x] este incrementat, iar grad[y] ramâne d. Deoarece nodul y nu mai este radacina, pointerul spre el din tabloul A este sters în linia 13. Deoarece dupa apelul HEAP-FIB-ÎNLĂNŢUIE valoarea grad[x] este incrementata, în linia 14 este restabilita proprietatea invariantului d = grad[x]. Ciclul cât timp este executat de atâtea ori pâna când A[d] = NIL, situatie în care nu exista alte radacini având acelasi grad ca si x. În linia 16 initializam A[d] cu x si efectuam iteratia urmatoarea ciclului pentru. Figurile 2.2 (c) - (e) prezinta tabloul A si arborii rezultati dupa primele trei iteratii ale ciclului pentru din liniile 4-17. La iteratia urmatoare a ciclului pentru sunt realizate trei legaturi; rezultatele lor se pot vedea în figurile 2.2 (f) - (h). Figurile 2.2 (i)-(l) prezinta rezultatele urmatoarelor patru iteratii ale ciclului pentru.
Ramâne sa definitivam operatiile începute. Dupa executia ciclului pentru din liniile 4-17, linia 18 videaza lista de radacini iar în liniile 19-26 aceasta este reconstruita. Heap-ul Fibonacci rezultat este redat în figura 2.2 (m). Dupa consolidarea listei de radacini, operatiile efectuate de HEAP-FIB-EXTRAGE-MIN se încheie cu decrementarea valorii n[H] în linia 15 si returnarea în linia 17 a unui pointer la nodul sters z.
Observam ca daca anterior apelului HEAP-FIB-EXTRAGE-MIN toti arborii din heap-ul Fibonacci sunt arbori binomiali neordonati, atunci arborii rezultati dupa apel sunt de asemenea binomiali neordonati. Arborii sunt modificati în doua feluri. În primul rând, în liniile 3-6 din HEAP-FIB-EXTRAGE-MIN, fiecare fiu x al lui z devine o radacina si fiecare arbore nou va fi un arbore binomial neordonat. În al doilea rând, arborii sunt înlantuiti prin HEAP-FIB-ÎNLĂNŢUIE doar daca sunt de acelasi grad. Deoarece înainte de crearea legaturilor toti arborii sunt binomiali si neordonati, cei doi arbori cu k fii au fiecare o structura de tip Uk. Rezulta ca arborele obtinut va avea o structura Uk+
Acum vom arata ca extragerea nodului minim dintr-un heap Fibonacci având n noduri are un cost amortizat O(D(n)). Fie H heap-ul Fibonacci pentru care aplicam operatia HEAP-FIB-EXTRAGE-MIN.
Calcularea costului actual al extragerii nodului minim poate fi facuta dupa cum urmeaza. O contributie O(D(n)) provine din faptul ca nodul minim are cel mult D(n) fii care sunt procesati de HEAP-FIB-EXTRAGE-MIN si din calculele efectuate în liniile 1-3 si 18-26 în procedura CONSOLIDEAZĂ. Ne ramâne sa analizam contributia din partea ciclului pentru din liniile 4-17. Dupa apelul procedurii CONSOLIDEAZĂ lungimea listei de radacini poate fii cel mult D(n)+t(H)-1, deoarece consta din nodurile initiale ale listei în numar de t(H), mai putin nodul radacina extras si plus numarul fiilor nodului extras care poate fi cel mult D(n). De fiecare data, în ciclul cât timp din liniile 6-16 una din radacini este înlantuita cu alta, astfel, calculul total efectuat de ciclul pentru este cel mult proportional cu D(n)+t(H). Astfel, timpul total de executie este O(D(n)+t(H)).
Înaintea extragerii nodului minim, potentialul este t(H)+2m(H), iar dupa extragere acesta este cel mult egal cu (D(n)+1)+2m(H), deoarece ramân cel mult D(n)+1 radacini si nu se marcheaza noduri în timpul efectuarii operatiilor. Astfel, costul amortizat este cel mult :
O(D(n)+t(H))+((D(n)+1)+2m(H))-(t(H)+2m(H))=
= O(D(n))+O(t(H))-t(H)=
=O(D(n)),
deoarece putem scala unitatile de potential pentru a depasi constanta ascunsa în O(t(H)). Intuitiv, costul efectuarii fiecarei legaturi se datoreaza reducerii potentialului în urma înlantuirilor care micsoreaza cu 1 numarul de radacini.
13.6 Marginirea gradului maxim
Pentru a demonstra ca timpul amortizat al operatiilor
HEAP-FIB-EXTRAGE-MIN si
HEAP-FIB-sTERGE este O(lg n), trebuie sa aratam ca
marginea superioara D(n) a gradului
oricarui nod dintr-un heap Fibonacci având n noduri este O(lg n). Atunci când toti arborii din heap-ul Fibonacci
sunt arbori binomiali neordonati, D(n) = [lg n]. Totusi,
taierile care se efectueaza în HEAP-FIB-DESCREsTE-CHEIE pot
genera arbori care nu respecta proprietatile arborilor binomiali
neordonati. În aceasta sectiune vom arata ca prin
înlaturarea unui nod de la parintele lui, daca acesta pierde doi
fii, atunci D(n) = O(lg n). Mai precis, vom arata ca D(n) <
[log f n], unde f = (1 + ![]() )/2.
)/2.
Ideea de baza a analizei este urmatoarea. Pentru fiecare nod x dintr-un heap Fibonacci fie dim(x) numarul nodurilor subarborelui cu radacina x, incluzându-l si pe x. (Sa observam ca x nu trebuie sa fie în lista de radacini - poate fi orice nod.) Vom arata ca dim(x) depinde exponential de grad[x]. Sa retinem ca grad[x] este actualizat pentru a exprima cu precizie gradul lui x.
Lema 13.2 Fie x un nod oarecare dintr-un heap Fibonacci si presupunem ca grad[x]= k. Notam cu y y yk, fiii lui x în ordinea în care au fost legati la x, de la cel mai devreme la cel mai recent.
Atunci, grad[y ] > 0 si grad[yi] > i-2 pentru i = 2,3,.,k..
Demonstratie. Este evident ca grad[y ]>0.
Pentru i > 2, observam ca atunci când yi a fost legat la x, celelalte noduri y ,y ,., yi-1 erau deja fii ai lui x, astfel ca grad[x] > i-1. Nodul yi este legat la x numai daca grad[x] = grad[yi], de unde rezulta ca la acel moment are loc de asemenea grad[yi] > i-1. Din acel moment nodul yi poate pierde cel mult un fiu, deoarece, daca si-ar fi pierdut ambii fii, ar fi fost taiata legatura sa cu x. În concluzie, grad[yi] > i-2.
Ajungem, în sfârsit, la acea parte a analizei noastre care justifica numele de "heap-uri Fibonacci". Dupa cum bine stim, pentru k = 0,1,2,., al k-lea numar Fibonacci este definit prin relatia de recurenta
0 daca k = 0
Fk = 1 daca k = 1
Fk--1 + Fk-2 daca k > 2
![]()
Lema urmatoare ofera un alt mod de a
exprima Fk.
Lema 13.3 Pentru orice k > 0,
k
Fk+2 = 1+ Fi .
i =0
Demonstratie. Demonstratia este prin inductie dupa k.
Daca k = 0,
0
1 + Fi = 1+ F0 = 1 + 0 = 1 = F
i =0
k-1
Presupunând acum ca are loc ipoteza inductiei, Fk+1 = 1 + Fi , avem:
i =0
k-1 k
Fk+2 = Fk + Fk+1 = Fk + ( 1 + Fi Fi .
i=0 i=0
Lema urmatoare si corolarul ei completeaza analiza. Lema foloseste inegalitatea:
Fk+2 > f k,
unde f este raportul de aur definit prin ecuatia Fk+2 = Fk + Fk+1 ca fiind :
f ![]() )/2 = 1.61803. .
)/2 = 1.61803. .![]()
![]() Lema 13.4 Fie x un nod oarecare dintr-un heap Fibonacci
si fie k =grad[x]. Atunci
Lema 13.4 Fie x un nod oarecare dintr-un heap Fibonacci
si fie k =grad[x]. Atunci
dim(x)> Fk+2 > f k , unde f ![]() )/2
)/2
Demonstratie. Notam cu sk valoarea minima posibila pentru dim(z) pentru toate nodurile z care au proprietatea grad[z] = k. Evident ca s0 s s2 = 3. Numarul sk este cel mult dim(z). Ca si în lema 4.1, notam y , y ,. ,yk fiii lui x în ordinea în care au fost legati la x.Pentru a calcula o margine inferioara pentru
dim(x) adunam 1 pentru x si 1 pentru primul fiu y (pentru care dim(y )>1) si aplicam apoi lema 4.1 pentru ceilalti fii. Avem astfel:
k
dim(x) > sk > 2 + s i-2 .
i=2
Aratam acum, prin inductie în raport cu k, faptul ca sk >Fk+2, pentru orice k nenegativ.
Cazurile de baza pentru k = 0 si k =1 sunt evidente.
Pentru pasul inductiv, presupunem ca k > 2 si si > Fi+2, pentru i = 0,1,.,k-1. Avem:
k k k
sk > 2 + si-2 > Fi = 1 + Fi = Fk+2
i=2 i=2 i=0
Ultima egalitate rezulta din lema 4.2.
Am aratat astfel ca dim(x) > sk > Fk+2 > f k
Corolarul 13.1 Gradul maxim D(n) al oricarui nod dintr-un heap Fibonacci având n noduri, este O(lg n).
Demonstratie. Fie x un nod oarecare al unui heap Fibonacci cu n noduri si fie k = grad[x]. Din lema 4.3 obtinem ca n > dim(x) > f k .
Logaritmând în baza f obtinem k < log f n. De fapt k < [log f n] deoarece k este întreg.
Gradul maxim D(n) al oricarui nod este astfel O(lg n).
Rezolvarea unor probleme dintre cele propuse.
Rezolvari la capitolul 1. Structuri elementare de date
Algoritm de intrare intr-o coada circulara alocata intr-un vector x cu n elemente, cu fata în f si sfârsitul în s.
Daca (s = n si f=1) sau (s=f-1) atunci 'DEPASIRE'
Altfel
s = s + 1
daca s>n atunci s=1
sdaca
x [ s ] = inf
sdaca
return
Algoritm de iesire dintr-o coada circulara alocata intr-un vector x cu n elemente, cu fata în f si sfârsitul în s.
Daca s = f atunci 'COADA VIDA'
Altfel
Inf = x [ f ] ;
f= f+1
Daca f>n atunci f=f+1
sdaca
sdaca
return
Doua stive alocate in acelasi vector :
a) Disciplina de umplere:
Presupunem ca la un moment dat sirul nostru va arata astfel:
|
V[1] |
V[2] |
V[3] |
V[k1] |
V[k2] |
V[n] |
Unde pâna la k1 avem prima stiva, iar de la k2 pâna la n avem cea de-a doua stiva.
b) Algoritmi de intrare-iesire a informatiei a pentru stiva 1:
Daca (k1 = n sau k1=k2-1) atunci 'DEPASIRE'
altfel
k1 = k1 + 1 ;
v[k1] = a ;
sdaca
return
Iesire_stiva1(V,n,k1,a)
Daca k1 = 0 atunci 'STIVA VIDA'
altfel
a = v[k1]
k1=k1-1
sdaca
return
c) Algoritmi de intrare-iesire a informatiei a pentru stiva 2:
Daca (k2 = k1+1 sau k2+n) atunci 'DEPASIRE'
altfel
k2 = k2 - 1 ;
v[k2] = a;
sdaca
return
Daca k2 = n atunci 'STIVA VIDA'
altfel
a = v[k2]
k2 = k2 + 1 ;
sdaca
return
Matrice patratica de ordin n in care toate elementele deasupra diagonalei principale sunt egale cu 0
d) Cate elemente pot fii
diferite de 0? : ![]()
e) Aranjarea elementelor pe linii intr-o coloana
Matricea :
|
A[1,1] | ||||
|
A[2,1] |
A[2,2] | |||
|
A[3,1] |
A[3,2] |
A[3,3] | ||
|
A[n,1] |
A[n,2] |
A[n,3] |
A[n,n] |
Sirul:
|
A[1,1] |
A[2,1] |
A[2,2] |
A[3,1] |
A[3,2] |
A[3,3] |
A[n,1] |
A[n,2] |
A[n,3] |
A[n,n] |
||
|
B[1] |
B[2] |
B[3] |
B[4] |
B[5] |
B[6] |
B[k-n] |
B[k-(n-1)] |
B[k-(n-2)] |
B[k] |
f) Formula pentru k:
![]()
g) Formulele pentru i si j:
Mai ramâne sa o faceti.
h) Algoritm de transformare din matrice in sir:
k = 0 ;
Pentru i = 1 la n
Pentru j = 1 la i
k = k + 1
B[ k ] = a [ i , j ] ;
Spentru
i) Algoritm de calcul pentru produsul normal este:
Prod_mat(A1,A2,n,MA)
Pentru j=1,n
MA[i,j]=0
Pentru k=1,n
MA[i,j]=MA[i,j]+A1[i,k]*A2[k,j]
Spentru
spentru
spentru
return
Pentru a gasi algoritmul dorit trebuie sa înlocuim:
A1[i,j] cu B1[(i(i-1)/2+j]
A2[i,j] cu B2[(i(i-1)/2+j] si
MA[i,j] cu MB[(i(i-1)/2+j].
Rezolvari la capitolul 2.
1. A=0.02 secunde
Viteza de revolutie pe secunda va fi R=7200/60= 120 R=1/120=0.0083 secunde
R/2= 0.00415
L/D=1000/80000=0.010205
Deci:
T=0.02+0.00415+0.010205=0.034355 secunde
Timpul total de citire a fisierului= 0.00415*8+0.010205*8000=81.6732, iar
Rezolvari la capitolul 3.
Modelul retea este un model care contine înregistrari, date si relatii 1 la mai multi între înregistrari.
Retelele sunt un mod natural de a reprezenta legaturile care se stabilesc între obiecte. În general retelele sunt reprezentate cu ajutorul unei structuri matematice numita graf orientat.
La modelul retea sunt doar doua structuri fundamentale si anume :
- îmregistrarea sau record (o colectie de date logic legate între ele)
- legatura sau set (o relatie de unu-la-mai-multe sau unu-la unu între doua
lnregistrari).
Sa consideram relatia Carte la Autor.
Carte
Autor
![]()
Aeasta relatie este, evident, multi la multi. Ea se transforma în:
Înregistrare de lagatura
![]()
Autor
Rezolvari la capitolul 4.
Ceea ce se transcrie în stuctura externa modelul ierarhic este o arboresceta grafica, un graf orientat, conex fara cicluri.
Sa consideram relatia Carte la Autor.
Carte
Autor
![]()
Aeasta relatie este, evident, multi la multi.
Aceeasi relatie folosita si la problema 2. cap 3. se va transforma:
Carte
Carteautor
Carteautor
Autor
![]()
![]()
În doua relatii 1 la multi în care dublarea lui 'Carteautor' se face în mod util.
Rezolvari la capitolul 5.
Rezolvari la capitolul 6.
INORD_IT(RAD)
STIVA = F {Stiva este vida}
P=RAD {P contine nodul care se viziteza}
Daca P ' * ' atunci{Parcurgere pe stânga}
P=>STIVA
P=LS(P) Cicleaza
altfel
EXIT
Sdaca
sciclu
{Parcurgere pe dreapta}
Daca STIVA = F atunci EXIT
Altfel
P<=STIVA ; Scrie INFO(P);P= LD(P)
Sdaca
Sciclu
Return
3. Arborele va fi:
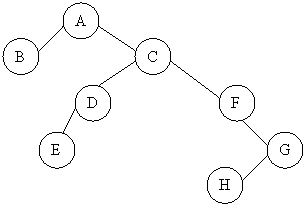
Rezolvari la capitolul 7.
Fiul stâng al nodului i se gaseste în 2i deci algoritmul va fi:
list_fara_stâng(a,n)
pentru i=1,n
daca a[i] '*' atunci
daca ((2i < n) si (a[2i] '*')) atunci
scrie a[i]
sdaca
sdaca
spentru
return
Rezolvari la capitolul 8. Arbori binari de cautare.
Exercitiul 1. (Determinarea nodului cu cheie maxima)
MAX_BIN (Rad, Max)
x = Rad
Atat timp cat LD(x) ≠ Nil x = LD(x)
Max = KEY(x)
sciclu
Return
Exercitiul 2. (determinarea predecesorului)
PRED_BIN(x, y)
Daca LS(x) ≠ Nil atunci
Cheama MAX_BIN(LS(x), y)
Return
sdaca
y = P(x)
Atat timp cat y ≠ Nil si KEY(y)>KEY(x) executa
y = P(y)
sciclu
Return
Exercitiul 3. (Cautarea binara recursiva)
CAUT_BIN_REC(Rad, k, Rez,x)
x = Rad
Daca x = Nil sau k = KEY(x) atunci
Return
sdaca
Daca k < KEY(x) atunci
Cheama CAUT_BIN_REC(LS(x), k, Rez,x)
Return
altfel
Cheama CAUT_BIN_REC( LD(x), k, Rez,x)
Return
sdaca
Rezolvari la capitolul 9.
1. h(k)=[m*((k*A) mod 1)] pentru A=( 5-1)/2=0.6180339
m=1000
(k*A) mod 1 pentru k=61 va fi 0.700
pentru k=62 va fi 0.318
pentru k=63 va fi 0.936
pentru k=64 va fi 0.554
pentru k=65 va fi 0.172
Deci locatiile vor fi respectiv 700, 318, 936, 554, 172.
2. Cu verificarea liniara se obtine aceasta secventa:
|
10 |
|
23 |
|
10 |
|
23 |
|
31 |
|
10 |
|
23 |
|
4 |
|
31 |
|
10 |
|
23 |
|
4 |
|
15 |
|
31 |
|
10 |
|
23 |
|
4 |
|
15 |
|
28 |
|
31 |
|
10 |
|
23 |
|
4 |
|
15 |
|
17 |
|
28 |
|
31 |
|
10 |
|
23 |
|
4 |
|
15 |
|
17 |
|
28 |
|
31 |
|
10 |
|
88 |
|
23 |
|
4 |
|
15 |
|
17 |
|
28 |
|
59 |
|
31 |
|
10 |
|
88 |
Cu verificare patratica cu functia h(k,i)=((k mod 11)+i+3i2) mod 11) se obtine:
Rezolvari la capitolul 10.
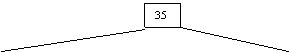
44
53 18![]()
![]() 18
18
![]()
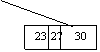
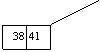
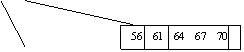
![]()
![]()
![]()
![]()
![]() 50 18
50 18
28
29
![]()
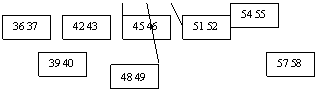
![]()
![]()
![]()
Pentru a insera cheia 60:
radacina e neplina
al doilea fiu al ei este tot neplin
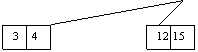
al treilea fiu al acestuia din urma este plin deci va trebui sa fie rupt:
Zona care ne intereseaza va arata asa:
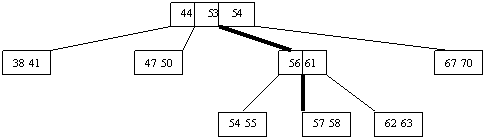
Pe calea îngrosata se va face inserarea. Dupa inserare aceeasi zona va arata:
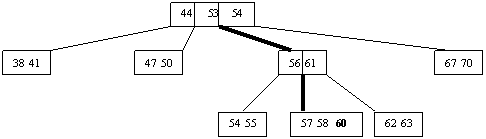
|