IMAGINILE OPERAŢIONALE ALE UNOR FUNCŢII UZUALE
FUNCŢIA ORIGINAL |
FUNCŢIA IMAGINE |
|
|
|
|
e-at |
|
|
|
|
|
sinwt |
|
|
coswt |
|
|
tn |
|
|
tcoswt |
|
|
|
|
8.5. UTILIZAREA TRANSFORMATEI OPERAŢIONALE LA CALCULUL RĂSPUNSULUI SISTEMELOR DINAMICE INVARIANTE CU ECUAŢII DIFERENŢIALE CU COEFICIENŢI CONSTANŢI
Se considera sistemul a carui MMII este dat sub forma unei ecuatii diferentiale:
anY(n)+a n-1Y(n-1)+.....a1Y'+a0Y= bmU(m)+b m-1U(m-1)+.....b1U'+b0U .
Determinarea variabilei Y(t) prevazute în cadrul capitolului 6 consta în gasirea solutilor ecuatiei diferentiale luând în considerare functia data de intrare U(t). Fata de acele procedee transformatele operationale au rolul simplitatii calculului si se pot realiza umarind urmatorii pasi:
Se transforma ecuatia diferentiala utilizând teoremele calculului operational. Astfel apare o relatie între imaginile operationale (U(S) si Y(S)) ale functiilor Y(t) si U(t) - ecuatia operationala.
Din ecuatia operationala se poate determina imaginea Y(S)=F[H(S),U(S),y(1),..U(1).] cu H(S) - functie ce depinde de coeficientii ec. difer.
Pentru gasirea lui Y(t) se executa în final o transformata inversa prin diferitele procedee prezentate în cadrul subcap. 8.4.
Exemplul 6. Sa se determine raspunsul liber al sistemului cu MMII:
Y''+3Y'+2Y=3U'+U cu conditile initiale: Y(0)=0 si Y'(0)=1
Raspunsul liber se calculeaza considerând U(k)(t)=0, atunci ecuatia MMII devine:
Y''+3Y'+2Y=0
Conform paragrafului 8.4.2.(teorema derivatei) se calculeaza imaginile operationale ale termenilor ecuatiei:
L[Y'(t)]=SY(S)-Y(0)=SY(S)
L[Y''(t)]=S2Y(S)-SY(0)-Y'(0)= S2Y(S)-0-1= S2Y(S)-1
De unde rezulta:
S2Y(S)-1+3SY(S)+2Y(S)=0
Y(S)=![]()
Se calculeaza polii numitorului: S2+3S+2=0, S1=-1 si S2=-2 si:
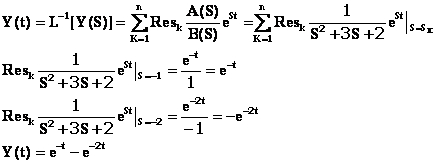

8.6. PROBLEME
|