INTELIGENTA ARTIFICIALA - Sintaxa limbajelor de primul ordin

Informatica

ALTE DOCUMENTE

Virus Goner win32

Rutare statica

Ce realizeaza urmatorul program:

Exsys Corvid

Modele ale Procesului de dezvoltare software

NOTIUNI GENERALE DESPRE CALCULATOR

INTERNET-UL

Grafica vectoriala

Configuratia hardware a unui calculator PC compatibil IBM

Prezentari electronice

INTELIGENTA ARTIFICIALA

I. Limbaje de primul ordin

Limbajele de primul ordin au fost introduse de Frege in 1879. Comparativ cu limbajul calculului cu propozitii, structura unui limbaj de primul ordin este mult mai complexa si ofera un cadru suficient pentru reprezentarea unei clase relativ largi de propozitii dintr-un limbaj natural. In contextul sistemelor bazate pe cunostinte, un limbaj de primul ordin este un sistem formal atasat unui astfel de sistem si permite proiectarea, analiza si controlul mecanismelor inferentiale in gestiunea cunostintelor stocate in baza de cunostinte a sistemului. Conventional, sistemul bazat pe cunostinte modelat prin intermediul unui anume limbaj de primul ordin, este referit ca interpretare intentionata pentru acel limbaj.

I.1. Sintaxa limbajelor de primul ordin

Vocabularul V al unui limbaj de primul ordin contine doua tipuri de simboluri si anume simbolurile logice si simbolurile non-logice. Spre deosebire de simbolurile logice, care sunt comune tuturor limbajelor din aceasta clasa, simbolurile non-logice sunt definite in functie de interpretarea intentionata pentru limbajul respectiv. Definirea multimilor de simboluri non-logice pentru construirea unui limbaj de primul ordin aferent unui sistem de cunostinte dat se numeste conceptualizare a sistemului.

Simbolurile logice sunt elementele multimii V U L U S U Q unde:

V este multimea variabilelor; V

L = este multimea simbolurilor de punctuatie.

Q = ^este multimea cuantificatorilor; simbolul V este cuantificatorul universal, respectiv

simbolul 3 este cuantificatorul existential.

Simbolurile non-logice sunt elementele multimii CS U FS U PS unde:

CS este multimea constantelor.

FS este multimea simbolurilor functoriale. Fiecare functor f FS este caracterizat de un

numar natural r(f) > 1 numit aritatea functorului f.

PS este multimea simbolurilor predicationale. Fiecare predicat x PS este caracterizat de un
numar natural r(x) ≥ 0 numit aritatea predicatului x.

Presupunem ca multimile V, L, S, Q, CS, FS, PS sunt doua cate doua disjuncte. Vocabularul

limbajului este V =VULUSUQUCSUFSUPS, elementele multimii A = V* se numesc asamblaje.

Pentru α A si x V , indicam prin <x(jc) faptul ca simbolul x apare cel putin o data printre simbolurile asamblajului α, respectiv prin a)jc( situatia contrara.

Intr-un limbaj de prim ordin identificam doua multimi de structuri simbolice de interes si anume multimea termenilor TERM si multimea formulelor FORM.

Definitia 1. Secventa de asamblaje t₁,,t_n este o secventa generativa termeni (SGT), daca pentru orice i, 1≤i≤n, t_i indeplineste una din conditiile: (i) t_i VUCS. (ii) Exista FSf si exista indicii jcui1,,j_r(f) 1 ≤j_p<, p = 1,,r(f) astfel incat

t =ft ,_t t .

t j1 ,t Jr(f)

Definitia 2. Numim termen orice asamblaj t cu proprietatea ca exista ≥ 1 si t₁,,t_n −SGT, astfel incat t_n =t. Multimea termenilor este notata TERM.

Reprezentarea conventionala a structurilor simbolice termeni este prin intermediul arborilor de structura.

Definitia 3. Arborele T directionat, cu radacina si varfurile etichetate cu simboluri din multimea FSV U CS U FS este un arbore de structura termen, daca pentru orice varfn al arborelui, i) daca od = 0, atunci cp(«) e V U CS ii) daca od > 1, atunci FS(n) e FS si r(q>(n)) = od(n). unde cp(ra) este eticheta varfului n.

Constructia unui arbore de structura T(t) pentru reprezentarea termenului t TERM poate fi realizata recursiv astfel:

a) daca t V U CS, atunci T() t = ()r, si cp(r) = t.

b) daca t = ft₁t_r(f) pentru anume f FS atunci

K/) unde r(f_i) = ()VTi,ETi, i = 1,,r(f), r este un varf nou, r UV()Ti si cp(r) = f.

Definitia 4. Multimea atomilor notata ATOM este

ATOM = lj jit_v.Jt_r(n)n e PS, /„.••,^_w e 7ERA/}.

Reprezentarea conventionala a atomilor este prin intermediul arborilor de structura. Pentru PS, r(π) = 0 arborele de structura este T(π) = (, <p(r) = π. Pentru π PS, r(n)> 1 si t₁,,t_r() g TERM, arborele de structura corespunzator atomului α = πt1t_r()π este

unde T()₍)()ti = ()Vt_i,Et_i este arborele de structura corespunzator termenului t_i, i = 1,,r(π) si

Definitia 5. Secventa de asamblaje α₁,,α_n este o secventa generativa formule (SGF), daca pentru orice i, 1≤i≤n, α_i indeplineste una din conditiile:

ii) exista i1 ≤ j < , astfel incat α_i = (—αj₎ ;

iii) exista < j,k < si exista L , astfel incat α_i = (αjρα_k );

iv) exista 1 ≤ j < i si exista x V, astfel incat α_i =

v) exista 1≤ j <i si exista x V, astfel incat α_i =

Definitia 6. Numim formula orice asamblaj α cu proprietatea ca exista n≥1 si α₁,,α_n −SGT, α_n = α. Multimea formulelor este notata FORM.

Observatie. Din definitia 5 rezulta ATOM FORM si daca α ATOM, atunci FORM. Convenim sa numim literal orice structura simbolica din multimea ATOMUATOM.

Convenim sa numim expresie orice structura simbolica din multimea TERMUFORM. Variabilele care apar in expresiile unui limbaj de prim ordin pot fi libere sau legate.

Pentru orice expresie α, notam cu FV(α) multimea variabilelor libere din α ,respectiv cu BV()α multimea variabilelor legate. Multimile FV, BV se calculeaza recursiv in modul urmator:

Pentru t TERM,

Pentru α FORM,

FV()α =

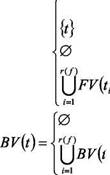
FV(t) =

daca t V daca t CS

daca t C ■) daca t = ft₁t_r(f),f FS

daca α PS,r(α)=

FV() _t i daca α = πt ₁.. .t_rw, π PS, r(n) > 1

daca α = ()β

FV()()β U FVγ daca α = ()βργ, ρ L -
FV()β x daca α = Vjc0 sau α = 3*0, x V

r(α) = 0

.t_r()π, π

daca α

, r()π ≥ 1

daca α =

BV()()α =

daca α = (

sau α = 3xp, x V

BV()()βUBVγ daca α = ( BV()βUx dacaα = '

Observatie. Din constructie rezulta ca pentru orice t TERM U ATOM, BV(t) = . De asemenea, ''legarea' unei variabile revine la prezenta in structura simbolica respectiva a unei cuantificari, existentiale sau universale, relativ la acea variabila.

Observatie. In general se doreste ca pentru orice formula α, sa nu existe cuantificari multiple asupra aceleiasi variabile si

FV(α)IBV(α).

Definitia 7. Daca α = VjcP FORM, atunci formula β este domeniul variabilei x. Analog, daca α = 3jcP, atunci domeniul variabilei x este β.

De exemplu, in formula α = Vjc((jcy →> Vx3y, BV(α^′)= . Cu toate caprin aplicarea acestei transformari structura simbolica reprezentand o formula se modifica, asa dupa cum va rezulta in sectiunea urmatoare, formula initiala si formula rezultata sunt echivalente din punct de vedere semantic.

Definitia 8. Spunem ca formula α este inchisa, daca FV(α) = . Multimea formulelor inchise este notata FORM₀. Daca FORMFORM si FV(α)= , formulele inchise

a = VjCjVjc_Ba, α = 3jCj3jc_Ba se numesc inchidere universala, respectiv existentiala atasata formulei

Definitia 9. Se numeste substitutie o multime de perechi θ = , unde t_t e ti

x_i V, x_i ≠ xj, x_i ≠ t_i pentru orice 1≤i≠ j ≤n.

Termenii t₁,,t_n se numesc termeni substituenti pentru variabilele substituite x₁,,x_n.

Substitutia θ este o substitutie de baza, daca in structurile simbolice corespunzatoare termenilor substituenti nu apar simboluri de variabile.

Substitutia vida, notata ε, corespunde multimii vide. Spunem ca θ este substitutie proprie, daca nici o variabila substituita nu are ocurente in termenul substituentpereche.

Multimea substitutiilor este notata SUBST.

Definitia 10. Fie t TERM, SUBST. Rezultatul aplicarii substitutiei θ termenului t, notat tθ, este definit prin:

t daca θ = ε sau t CS sau

t Vx₁,,x_n, θ = _t1x1,,tnxn

t_idacat = x_i _x1,,xn

1θt_r()fθ daca t = ft1t_r()

Observatie. Din definitia 10 rezulta imediat ca pentru orice t TERM, SUBST, tθ TERM.

Observatie. Fie t TERM, SUBST. Arborele de structura T(tθ) rezulta prin aplicarea arborelui de structura T()t a transformarii constand in substituirea varfurilor terminale ale caror etichete sunt variabile substituite de θ, prin arborii de structura corespunzatori termenilor asociati in substitutia θ. Cu alte cuvinte termenul tθ rezulta prin substituirea in structura simbolica t a fiecarei variabile substituite de θ prin termenul pereche corespunzator.

Definitia 11. Fie ATOM, SUBST. Rezultatul aplicarii substitutiei θ atomului α, notat αθ, este definit prin:

fa daca α PS, r(α) = 0

a9 = <

I πt t_r(π) θ daca α = πt ₁.. t_r(

Evident αθ ATOM.

Definitia 12. Fie α FORM ATOM, θ SUBST. Rezultatul aplicarii substitutiei atomului α, notat αθ, este definit prin: i) daca θ = ε, atunci αθ = α ;

ii) daca θ=, atunci

daca α = (-β)

daca α = ()βργ, ρ L

Vjc09 daca α = V*p x x₁,,x_n}

3jc09 daca α = 3x0, x x₁,,x_n

daca α = 3jc0 sau α = Vjcp

Evident, pentru orice α FORM si θ SUBST FORM.

Observatie. Din definitiile 10-12 rezulta ca daca α FORM U TERM SUBST, atunci a9 rezulta prin substituirea variabilelor libere din α prin termenii pereche corespunzatori in substitutia θ. In particular, daca α FORM₀, atunci αθ = α pentru orice θ SUBST.

Definitia 13. Fie S_UBST λ,θ . Compunerea substitutiilor θ, notata λ -9 este definita

prin i) ii) iii)

daca θ = ε, atunci X-Q daca λ = ε, atunci λ daca θ ≠ ε si λ ≠ ε, atunci λ • θ rezulta din multimea

t₁θx₁,,t_nθx_n,s₁y₁,,s_my_m

y_} pentru care

prin eliminarea perechilor t_iθx_i pentru care tiθ = x_i si a perechilor

y_j _x1,,xn, undeλ = t₁x₁,,t_nx_n, θ = .

Observatie. Operatia de compunere a substitutiilor nu este comutativa. Pentru orice λ, θ, r| substitutii proprii λ • (9 • r) = λ • 9)- η.

Daca E TERM U ATOM, atunci E(λ ■ θ) = (Eλ)θ.

Definitia 14. Fie E = E₁,,E_n TERM ATOM. Substitutia θ este substitutie unificator pentru E daca, E,n_iθ = E_jθ₁ ≤i,j≤. Multimea E este unificabila, daca exista

substitutie unificator pentru E. Daca θ este substitutie unificator pentru E, spunem ca Eθ = este singleton.

Definitia 15. Fie E multime unificabila. Substitutia unificator σ este un cel mai general unificator pentru E, daca pentru orice substitutie unificator θ exista _λ SUBST, astfel incat 9 = σ • λ. Substitutia cel mai general unificator este referita prin termenul de mgu (most general unifier) pentru multimea data.

Definitia 16. Dezacordul D(e) al multimii E = TERMUATOM este

multimea rezultata prin retinerea cate unei subexpresii din fiecare expresie din E, incepand cu prima pozitie in ordinea de la stanga la dreapta in care cel putin doua expresii difera.

Observatie. Arborii de structura corespunzatori elementelor din D()E sunt subarborii arborilor de structura ai expresiilor din E avand radacinile primele varfuri in traversarea top-down si left-to-right cu etichete distincte.

Verificarea proprietatii ca o multime E TERM U ATOM este unificabila/neunificabila si calculul unui mgu in cazul in care E este unificabila pot fi realizate pe baza procedurii de unificare Robinson.

procedure UnificareRobinson(E:MultimeExpresii);

W₀←E ← ε ; k ← 0 ; gata ← false ;

repeat

if (W_k este singleton) then

write('E este unificabila', σ_k, 'mgu pentru E') ; gata ← true else

calculeaza()Wk, D_k;

if exista()x,t,Dk then alege (x_k,t_k,D_k) ;

else

write('E nu este unificabila'); gata ← true

endif endif

until gata end;

Apelurile de proceduri initiate de procedura Unif icareRobinson determina urmatoarele actiuni:

calculeaza (W, D): calculeaza D dezacordul multimii W,

exista (x, t, D): returneaza true, daca si numai daca exista x VID si exista t TERM I D, astfel incat t)x(. alege (x, t,D) : selecteaza x VID si t TERMID astfel incat t)x(.

Teorema 1 (Teorema de unificare Robinson) Procedura Unif icareRobinson este un algoritm care decide corect asupra proprietatii de a fi unificabila, respectiv neunificabila a multimii E. Daca E este unificabila si calculul se termina cu W singleton, atunci kσ_k este un mgu

pentru E.

Observatie. Mecanismul de unificare descris de procedura Unif icareRobinson revine la tentativa de 'reparare' a dezacordurilor existente in structurile simbolice din multimea E, prin aplicarea, atunci cand este posibil, de substitutii cu efect de unificare local. Din teorema 1 obtinem ca dezacordurile 'nereparabile' sunt de doua categorii:

a) t₁ V, t₂ V si frontchar()t1≠ frontchar(t₂), unde frontchar(t) reprezinta primul simbol al
structurii t,

b) t₁ V, t₂ V si t₂{t_x).

I.2. Semantici pentru limbajele de primul ordin

Definirea unei semantici presupune in primul rand acordarea fiecarui simbol non-logic a unei anumite semnificatii si anume: semnificatia fiecarui functor sa fie aceea de functie cu numar de argumente egal cu aritatea functorului, semnificatia fiecarui simbol predicational sa fie aceea de predicat care exprima o relatie intre un numar de obiecte egal cu aritatea simbolului, respectiv semnificatia fiecarei constante sa fie aceea de individ particular din domeniul suport. Semnificatiile acordate simbolurilor non-logice induc in continuare semnificatii pentru structurile din multimea TERMUFORM si anume: expresie functionala pentru structurile simbolice de tipul termen,

predicate desemnand relatii intre expresii functionale pentru atomi si respectiv expresii logice rezultate prin utilizarea mai multor predicate si a cuantificatorilor pentru formulele limbajului.

Multimea functiilor definite pe multimea A cu valori in multimea B este notata [] A → B.

Definitia 1 Fie L un limbaj de primul ordin. Perechea (D,I) se numeste L− structura(, unde D este o multime nevida numita domeniu de interpretare si I = (I_Cs,Ifs,Ips ),

I_CS:CS→D;

I_FS : FS - Q [Dⁿ I astfel incat pentru orice FSFS:FS→U∞[]Dn→Df , I_FS (f): D^r(f) → D;

i=1

I_PS :PS→U∞[]Dⁿ →DUT,F, astfel incat pentru orice π PS, I_PS()π:D^r(π) →

i=1 daca r()> 1, respectiv I_PS() g daca r(π) = 0.

Convenim sa notam: I_CS()a=∆a^I, I_FS()f=∆f^I, IPS⁽)π^=∆π^I; ^aI , f^I ,π ^I sunt respectiv interpretarile constantei a, a simbolului functorial f si a simbolului predicational π in L − structura

Fie M = ()D,I o L− structura(. Semnificatia fiecarui termen t TERM, notata t^I, este aceea de rezultat al evaluarii arborelui de structura T(t) conform regulilor de calcul asociate de L−structura M simbolurilor functoriale cu ocurente in structura simbolica t si a interpretarilor considerate pentru simbolurile din multimea CS. Evaluarea arborilor de structura necesita insa ca si variabilele din structurile simbolice din multimea TERM sa aiba ''atribuite valori'' din domeniul de interpretare D. Cu alte cuvinte, simbolurile din V etichete ale unor varfuri din T()t) corespund unor locatii de memorie carora M nu le aloca informatie. Evident, intr-un arbore de structura numai varfurile terminale pot avea etichete simboluri din V.

Numim asociere (valuatie) orice functie s : V » D.

Definitia 2. Fie s []V → D, x V, a D. Notam cu s[x := a] g V →» D asocierea definita prin

(s(y) daca y ≠ x

[a daca y = x Pentru n≥1, daca Vx₁,,_x gF, a_l ,,a n asocierea s^ :=a₁,,x_n := a_n] este definita

recursiv de relatia

r ir ti

4*! := a₁,,x_n := a_n = s[x₁ := a1,,xn−1 := a_n−1][x_n := a_n].

Observatie. Daca x₁,,x_n V sunt astfel incat pentru orice 1≤i≠ j ≤n, x_i ≠ xj, atunci

pentru orice permutare σ a multimii rezulta

f ._ _ 1_ I I

Daca x V, a,b D astfel incat s[x := a, x := b] = s[x := b], deci in cazul in care variabilele x₁,,x_n nu sunt distincte doua cate doua,

x1 := a₁,,x_n := a_n≠ s[x_σ(1) := a_σ(1),,x_σ(n) := a_σ(_n)].

Definitia 3. Fie M = ()D,I o L − structura(. Semnificatia t^I indusa de Mpentru termenul t TERM este t^I [] V→ D→ D definita prin,

t^Idaca t CS

s(t daca t V

: = ft1t_r(f)

Observatie. Procedeul descris revine la traversarea cu evaluare top-down a arborelui rezultat prin transformarea arborelui de structura al termenului conform L − structurii si a asocierii s considerate. Arborele transformat rezulta prin substituirea etichetelor simboluri functoriale si constante prin valorile functiilor I_FS, respectiv I_CS si substituirea fiecarei etichete x V prin s(x).

Calculul valorii t^I (s) poate fi realizat prin traversarea cu evaluare bottom-up a arborelui de structura transformat.

Valoarea t^I (s) D este informatia asociata varfului radacina rezultata la terminarea traversarii.

Semnificatia indusa de o L− structura( M = (D,I) structurilor simbolice din multimea ATOM este de predicat ce exprima o relatie intre termenii argumente.

Definitia 4. Fie M = ()D,I o L− structura( si ATOM. Interpretarea atomului α in

L − structura M = ()D,I, este α^I []V D → definita prin,

dacaα PSr(α) = 0

Observatie. Similar structurilor simbolice de tipul TERM, daca α ATOM, atunci valoarea α^I (s) T,F rezulta ca informatie asociata varfului radacina prin traversarea cu evaluare bottom-up a arborelui de structura corespunzator atomului α.

Pentru construirea semanticii induse de o L − structura( formulelor limbajului, introducem operatorii ()A_x _x_V,()E_xx_V

definiti in modul urmator: pentru orice se[F^/)]-> ] si orice s [V→D], (A_x(q>))(s) = T, daca si numai daca pentru orice a D, q>(s[x := a]) = T, ()E_x(cp)X'S') = T, daca si numai daca exista a D astfel incat q>(s[x := a])=T.

Semantica indusa de o L− structura( M = (D,I) fiecarei formule α a limbajului, notata

α^I, este similara semanticii induse pentru atomii limbajului si anume α^I este functie definita pe

multimea asocierilor cu valori in multimea , α^I : [V →> D] → .

Este suficient sa definim α^I pentru α FORM ATOM.

Definitia 5. Fie M = ()D,I o L− structura( si α FORM ATOM. Pentru orice

s []V→D, interpretarea α^I : [] V → D → a formulei α in M este definita prin

β^I(^s) dacaα

β^I (s) v γ^I (s) daca α = () β y) I⁽s)→γI⁽s) daca α = () β→ γ. P⁷(5)^y⁷(5) dacaa = (p^y)

Spunem ca asocierea s valideaza α, daca α^I(s) = T, respectiv s falsifica α, daca α^I(s) = F. Convenim sa reprezentam prin M = α[s] faptul ca s valideaza

Definitia 6. Fie M = ()D,I o L− structura(, σ SUBST. Compunerea valuatiei s [] V → D cu substitutia σ este valuatia s ■ σ definita prin

daca σ = ε

{s[_Xl :=t1I(s),,x_n :=t_nI(s) dacaσ = _t1_x1,,tnxⁿLema 1. Fie M = ()D,I o L− structura(, s [V → D] a = SUBST.

Pentru orice TERM U FORM, ()ασ^I (s) = α^I (s ■ σ).

Corolar. Daca M = ()D,I este o L−structura(, α FORM, σ = SUB ST, atunci α este validabila in M daca si numai daca ασ este validabila in M.

Intr-adevar, deoarece pentru orice α FORM, (aa) (s) = α^I(s-a) obtinem M=ασ(s),

daca si numai daca M =α()s ■ σ.

Definitia 7. Fie M = ()D, I o L − structura( si α FORM. Spunem ca α este validabila (satisfiabila) in Mdaca exista s []V→ D, astfel incat M = α[s]. Formula α este validabila, daca existA o L − structura( M, astfel incat α este validabila in M.

Definitia 8. Formula α este valida in L − structura M, daca M = α[]s pentru orice

asociere s. In acest caz spunem ca M este model pentru α si notam M =α. Multimea modelelor formulei α este notata M()α.

Lema 2. Fie M = ()D,I o L− structura(. Daca a F ORM α TERMU, astfel incat FV()α = , atunci pentru orice s₁,s₂ [V → D], α^I (s₁) = α^I (s₂).

Corolar. Fie α FORM₀. Daca M = (D,I) este o L− structura( atunci α este validabila

in M, daca si numai daca α este valida in M.

Definitia 9. Formula α este valida (tautologie), daca α este valida in orice L − structura

Reprezentam formulele α valide prin

Observatie. Pentru α FORM, FV(α)= fie α = Vjc₁Vjc_bcc, α = 3x_l..3x_na inchiderile universala si respectiv existentiala ale formulei α. Evident α, α FORM₀. Pentru orice L − structura( M = ()D,I, α este validabila in M, daca si numai daca α este validabila in M, deci

daca si numai daca α este valida in M. De asemenea, α este valida in M, daca si numai daca α este valida in M.

Lema 3. Formulele (Vjca α→ 3jca), (BjcVya -^ VyBjca) sunt valide pentru orice a FORM, x,y V, x≠y.

In particular rezulta ca existA formule valide. Se demonstreaza cu usurinta ca un alt exemplu de formula valida este () v (-ia)). Convenim sa notam cu | o formula valida arbitrara.

Definitia 10. Formula α este invalidabila daca pentru orice L − structura( M si orice valuatie s, α^I (s) = F.

Observatie. Exista formule invalidabile. Intr-adevar, pentru orice α FORM, (a a (-α) este formula invalidabila. Convenim sa notam cui o formula invalidabila oarecare.

Definitia 11. Multimea de formule H este validabila, daca exista o L − structura( M si exista s [] V → D, astfel incat M = α[]s pentru orice α H.

Definitia 12. L − structura M este model pentru multimea de formule H daca M este model pentru toate formulele din H. Convenim sa notam in acest caz, M = H.

Daca M()H este familia modelelor multimii H, atunci

M(H)=

Definitia 13. Multimea de formule Heste valida, daca orice L − structura Minebreak Meste model pentru H. Proprietatea de validitate a unei multimi de formule H este reprezentata = H.

Definitia 14. Fie H FORM. Formula α este consecinta logica a multimii H, daca pentru orice L− structura( M si orice s V → D], astfel incat Tβ^I (s) = T pentru toate formulele H, rezulta α^I (s) = T. Daca α este consecinta logica a multimii H, notam H =α.

Lema 4. Daca H FORM₀, α FORM₀, atunci H= α, daca si numai daca H U

este invalidabil.

Lema 5. Daca H = α₁,,α_n FORM₀, α FORM₀, atunci H =α, daca si numai daca

|=(p„ ->a) unde p, =a„ p,. =(a,. aP_m), i = 2,,n.

Definitia 15. Formulele α, β sunt logic (semantic) echivalente, notat α ≡ β, daca pentru orice L − structura( M = ()D,I si pentru orice valuatie s [V→ d], α^I(s) = β^I(s).

In particular, daca α, β sunt formule inchise, atunci α ≡ β, daca si numai daca au aceeasi familie de modele, M()()α = Mβ.

Observatie. Relatia de echivalenta semantica este o relatie de echivalenta pe multimea formulelor.

Lema 6. Pentru orice a,P α ,β , x V

i) (a^pHa->p)A(p->cc);

ii) ()₍) α≡ α→ l);

iii) (a^pH(^a)vp);

iv) α ≡ β daca si numai daca =() α↔ β;

vi)

Lema 7. Pentru orice FORM, x V, astfel incat α ≡ α^′ si β ≡ β^′,

ii) ()() = (a'pP')pentru ρ L ;

iii) (Vjca) = (V;ca');

iv) (3jca) = (3jca').

Lema 8. Pentru orice FORM,

i) av_L = a, aa_L = _L;

ii) α v | ≡ | . α a | ≡ α ;

iii)

iv) HoAp))-((-no)v(-,p));
v)
vi)

vii) (a a (p v y)) = ((a a p) v (a a y)), (a v (p a y)) = ((a v p) a (a v y));

viii) (a a () α p)) ≡ α, (a v () p)) ≡ α ;

ix) (av(pvy))-((avp)vy), (aa(PA_Y))-((aaP)a_Y).

Observatie. Pe baza proprietatilor stabilite de lemele precedente, rezulta ca pe multimea

claselor de echivalenta FORM = FORM _≡ poate fi identificata o structura de algebra Boole

A A

(algebra Lindenbaum asociata limbajului), cu primul element 0 = _L si 1 = | ultimul element, unde

Lema 9. Fie FORM, x V, astfel incat P)jc<
i) (Vjcavp) = Vjc(avp);

ii) (3jcavp)=3jc(avp); iii) (VjcaAp)=Vjc(aAp); iv) (3jcaAp) = 3jc(aAp); v) (Vjca v Vjcp) = Vjc(a v p); vi) (3jca a 3jcp) = 3jc(a Ap).

Lema 10. Pentru orice α FORM, x V i) Vjca = (^3jc(^a)); ii) 3jca = (-,Vjc(-,a)).

Lema 1.2.11. Pentru orice FORM, x,y V, t TERM,
i) 3jc3ycc = 3^3jca ;

ii) VjcVycc = Vy Vjca ; iii) (Vjca^a) = J; iv) -> 3jca) = J.

I.3. Repezentari normalizate pentru formulele limbajelor de primul ordin

Definitia 1. Formula inchisa α este o forma normala prenex daca α = Q₁x₁Q_nx_nβ, unde FV()α = x₁,,x_n, Q_i e, 1≤i≤n, β FORM, P)3(, P)V(. Secventa Q₁x₁Q_nx este prefixul, respectiv β este matricea formulei α.

Teorema 1. Pentru orice FORM₀, existaα forma normala prenex si

Definitia 2. Se numeste clauza orice disjunctie de literali. Clauza vida, notata

este

clauza corespunzatoare multimii de literali vida. Clauza vida este prin definitie invalidabila.

Cu alte cuvinte, daca L = L₁,,L_n a ATOM U —ATOM este o multime de literali atunci o

disjunctie a de literalilor din multimea L este k = β_n unde β1 = L₁, β_j = (p^j v Lj), 2 ≤ j ≤ n.

Literalii atomi se numesc literali pozitivi, respectiv literalii negatii de atomi se numesc literali negativi.

Evident, M()βj = UM(₎ Li, 1 ≤ j ≤ n, deci M(k) = UM()L_i) si pentru orice permutare σ a

i=1 i=1

multimii 1,2,. ..,n, βn ≡ γ_n unde γ₁ = L_σ(1), γ_j = (y^j vL_o(j)), 2 ≤ j ≤ n, deci oricare doua clauze

asociate aceleiasi multimi de literali au aceeasi semnificatie. In particular, putem presupune ca ordinea in care sunt considerati literalii este astfel incat literalii pozitivi ai clauzei (daca exista!) au

cei mai mici indici. Conventional clauza k este reprezentata V L_i si pentru simplificarea scrierii omitem parantezarea impusa de regulile de sintaxa considerate.

Fie k = VnL_i clauza. Presupunem ca =ATOMI si L_j=(A_j), m + 1≤ j ≤n sunt literalii negativi ai clauzei k. Rezulta,

^! i=ro+r ^ i=m+l

Definitia 3. Daca L = L₁,,L_n —ATOM atunci k = V ^L i se numeste clauza scop sau scop definit.

Fie k = Vn()—A_i clauza scop, A_i ATOM, i = 1,,n. Evident,

n n n —

k ≡ —ΛA_i v—iAA_i=AA_i-> deci L−structura M = (D,I) este model pentru k daca si

r i f' V

numai daca pentru orice valuatie s [V → D], A A_t (s) = F, deci daca si numai daca pentru

orice valuatie s []V→D, exista i, 1≤i≤n astfel incat A (s) = F.

Clauza k este clauza definita (sau clauza Horn), daca n = 1 si L ATOM sau n ≥ 2 si L₁ ATOM , L₂,,L_n —ATOM . In primul caz, clauza k se numeste clauza fapt, respectiv in cel de al doilea caz k se numeste clauza regula.

Fie k = L_xv V L_{, α este o forma normal
conjunctiva}

daca α = γn unde γ₁ = k₁, _γj = (γ_j−1 Akj),2<j<n.

Evident, M()γ_j=^IM()k_i, 1≤j≤n deci M()()α=^IMk_i si pentru orice permutare σ a

i=1 i=1

multimii 1,2,,n, βn ≡δ_n unde δ₁ =kσ₍₁ ),δ_j = (δ_j−₁ ^K_(j)), 2≤j≤n.

Conventional formula α este reprezentata α = Λ k_i si pentru simplificarea notatiei

i=1

eliminam parantezarea dictata de sintaxa. Multimea de clauze S = se numeste reprezentare clauzala pentru orice forma normal conjunctiva asociata multimii de clauze.

Fie α forma normal conjunctiva avand reprezentarea clauzala S = k₁,,k_n. Deoarece

M()α= IM(k), rezulta ca toate formele normal conjunctive atasate aceleiasi multimi de clauze

sunt semantic echivalente. Forma normal conjunctiva atasata multimii de clauze vide se numeste formula vida si este notata ' 0 '. Formula vida este prin definitie tautologie.

Definitia 5. Forma normala prenex α = Q₁x₁Q_nx_nβ este o forma normala Skolem daca Q,i V, 1 ≤ i ≤ n si β este o forma normal conjunctiva.

Lema 1 (Transformarile de normalizare Skolem). Fie α = Q₁x1Q_nx_nβ forma normala prenex. Formula α este validabila daca si numai daca α₁ este validabila, unde

Q₂x₂Qnxnβax1,

daca Q1 = 3 unde a Cs, P)a(

Afx^x} =V,l<j<i,Q_M =3

Teorema 2. Pentru orice α FORM₀, exista α forma normala Skolem astfel incat α este validabila daca si numai daca α este validabila.

Definitia 6. Fie α FORM₀ si α = Vjc₁Vjc„P forma normala Skolem astfel incat α este

validabila daca si numai daca α este validabila. Daca β = Λn_ki atunci S()α=k₁,,k_n este o

reprezentare clauzala pentru

Clauzele unei reprezentari clauzale sunt subintelese formule inchise cu toate variabilele cuantificate universal, deci M = ()D,I este model pentru α daca si numai daca pentru orice a₁,,a_n D,

s^[x₁ :=a₁,,x_n :=an])+ T, deci daca si numai daca pentru orice a₁,,a_n D,

k.

Elementele multimii B_H se numesc atomi Herbrand. Evident, daca ATOM si FV()α=x₁,,x_n,atunci pentru orice t₁,,t_n H_∞(S), α este un atom de baza. Elementele multimii B_HU-B_H se numesc literali Herbrand.

Definitia 2. L−structura M = (H_∞(S),I*) este H−interpetare (interpretare Herbrand), daca indeplineste urmatoarele conditii: i) pentru orice a CS, I*_cs (a) = a^I * =;

ii) pentru orice f FS, I_FS*(f)=f^I ^*: H∞r(^f) →>H_∞(S) astfel incat pentru orice t₁,,t_r(f) H∞, f¹ [t_l,,t_r(f))=ft_lt_r(f.

Definitia 3. H−interpretarea M =(H_∞,I*) este model Herbrand (H−model) pentru multimea de formule inchise S daca pentru orice S si orice valuatie s e V →H∞,

α^I*(s) = T.

Multimea H −interpeta(rilor se corespunde cu multimea submultimilor multimii B_H si anume, H−interpetarea H_X,I j se identifica prin multimea literalilor Herbrand γ B_H(^S)

validati de (&„,/*); / =T.

Fie M* =(H∞,I*) o H−interpretare oarecare. Deoarece B_H este o multime cel mult numarabilA, putem considera sirul elementelor din B_H, fie acesta (A_n )_n=1, ₂ ,

Rezulta ca M* se corespunde cu sirul (B_n )_n=1, ₂, , unde

daca A^I* = T

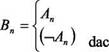* ,n = 1,2, aA^ =F

In mod frecvent, universul Herbrand si baza Herbrand sunt definite relativ la o multime finita de formule. In aceste cazuri, in constructiile multimilor H_∞ si B_H intervin numai simbolurile non-logice, constante, simboluri functoriale si simboluri predicationale, care au ocurente in formulele multimii considerate.

Definitia 4. Fie S multime finita de clauze;

C(S) =

F(S) = P(S) = . Definim sirul de multimi ()H_n(S)_n_N prin

C{S) dacaC(S)≠

Evident, pentru orice n ≥ 0 H_n(S) TERM si structurile simbolice din H_n()S nu contin simboluri din multimea V. Elementele multimii H_n (S) se numesc constante Herbrand de nivel n. In

general atributul ''de baza'' este asociat structurilor simbolice in care nu exista simboluri desemnand variabile.

Multimea H_∞(S) = UH_n(S) este universul Herbrand al multimii de clauze S. Elementele

n=0

multimii H_∞ (S) se numesc constante Herbrand. Evident, orice constant Herbrand este termen de baza dar nu si reciproc. De exemplu, daca t TERM si FV(t) = , atunci pentru orice t₁,,t_n H_∞(S), tt₁x₁,,t_n x_n este un termen de baza dar nu este in mod necesar constanta Herbrand. De asemenea, daca k este o clauza/literal si FV(k) = atunci pentru orice t₁,,t_n H_∞(S), kt₁x₁,,t_n x_n este o clauza/literal de baza. Definitia 5. Fie S o multime finita de clauze;

P(S) = Baza Herbrand este Hy) - T^tl'-^tr(P) ' ^e '^h *1> —>'_r(i>) ^e ^Hn-)>

elementele multimii B_H(S) se numesc atomi Herbrand.

Evident, B_H(S) ATOM si orice atom Herbrand este un atom de baza. Daa α ATOM, FV(a)= atunci pentru orice t₁,,t_n H_∞(S), α este un atom de baza. Elementele multimii B_H(S) U -BH(S) se numesc literali Herbrand.

Definitia 6. Fie S o multime finita de clauze. L−structura M = (H_∞,I*) este H − interpetare (interpretare Herbrand), daca indeplineste urmatoarele conditii:

i) pentru orice a C(S), I_cs *(a) = aI^* = a ;

ii) pentru orice f f(S), I_FS* (f): H∞^r(f) (S) → H_∞ (S), astfel incat pentru orice

Definitia 7. Fie S multime finita de clauze. eaH − interpetar M = (H_∞,I*) este model Herbrand (H −model) pentru S daca pentru orice k S si orice valuatie s [] V → H∞(S),

k^I*(s) = T.

Multimea H − interpreta(rilor se corespunde cu multimea submultimilor multimii B_H (S) si anume, H − interpretarea (H∞,I*) se identifica prin multimea literalilor Herbrand γ B_H(S)

validat de (#„,,/*); / =T.

Fie M* =(H_∞(S),I*) o H−interpetare oarecare. Deoarece B_H(S) este o multime cel mult numarabila, putem considera sirul elementelor din B_H (S), fie acesta (A_n )_n=1, ₂ ,

Rezulta ca M* se corespunde cu sirul (B_n )_n=1, ₂, , unde

daca AI_* =T

,n = 1,2,.

dacaAIn* =F Definitia 8. Fie functia y.H^S)^ D definita prin,

t' daca t C(S)

i/⁷^,),-,^/))) dacat = ft₁t_r(f)

unde M = ()D,I este o L− structura(. Daca S este o multime finita de clauze, atunci clasa H− interpreta(rilor M* =(H_∞(S),I*) induse de M este definita prin:

- I_CS*(a) = a^I* H_∞(S) astfel incat pentru a C(S), a^I* = a^I;

I_FS*(f) = f^I* :H∞r(f)(S) → H_∞(S) cu restrictia ca daca f F(S) atunci pentru orice

IP_S*()π=π^I* :H∞^r()π(S)→T,F cu conditia ca daca P(S) atunci pentru orice

Evident, Hinterpretarile−( induse de M coincid pe multimea C(S)UF(S)UP(S) a simbolurilor non-logice care apar in clauzele din S.

Lema 1. Fie L−structura M = (D,I), S multime finita de clauze si M* = (/^(S),/ j o H−interpretare indusa de M. Pentru orice t C(S)UVUTERM(F(S)) si pentru orice

je[F^ H_x (S)], (t>Y (s))= ^MO)' ^unde ^'-HA^^D este functia definita in definitia 1.4.5., (t>(s) [] V → D, astfel incat pentru orice x V, <p(s)(x) = (p(^(jc)) si TERM()F(S) este multimea termenilor t cu proprietatea ca toate simbolurile functoriale care au ocurente in t apartin multimii F.(S)

Teorema 1. O multime finita de clauze este validabila daca si numai daca admite un model Herbrand.

Observatie. Concluzia stabilita de teorema 1 nu mai ramane adevarata pentru multimi finite arbitrare de formule inchise. Intr-adevar, fie A = , π PS, r()π = 1, a CS.

Fie L − structura M = ()D,I, D = , astfel incat a^I = 0, π^I (0) = T, π^I (1) = F. Deoarece

()-πxI()s[]x := 1 = -₍πx)I(s[x := 1])=π^I(s[x := 1]) = T rezulta (3x(-^nx)Y (s) = T.

Obtinem astfel ca pentru orice s [V→ ]

(πx))^I (s) =

= (3x(-,nx)Y(s) = T deci M este model pentru S.

Pe de alta parte, α = ()π a 3jc(-.tdc)) ≡ 3x(na a (—_πx)) deci α = (πa a ()—πb) este o forma normala Skolem pentru α, ceea ce determina S(α)= , unde b CS, b≠a. Deoarece H_∞(S) = a,b si B_H(S) = πa,πb rezulta ca nu exista H−modele pentru S.

Definitia 9. Fie S multime finita de clauze, variabilele care apar in clauzele din

S. Substitutia θ = t1x1,,tn x_n este substitutie de baza pentru S daca t_i H_∞(S), i = 1,n.

Evident daca θ = t1x1,,tn x_n este substitutie de baza pentru S = , atunci k_iθ,

i = 1,n sunt clauze de baza. Clauzele k_iθ, i = 1,n se numesc instantieri de baza pentru clauzele din

S.

Din teorema 1. rezulta ca multimea de clauze S este invalidabila daca si numai daca orice H−interpretare falsifica cel putin o clauza din S. Explorarea sistematica a spatiului tuturor H − interpeta(rilor poate fi efectuata in mai multe moduri, unul dintre acestea este metoda bazata pe arbori semantici propusa de Robinson 1968, Kowalski 1969 si Hayes 1969. Ideea se bazeaza pe observatia ca orice H−interpetare corespunde cu submultimea multimii B_H(S)a atomilor Herbrand validati de interpretarea respectiva, metoda revenind la extinderea incrementala a H − interpreta(rilor partial generate. Deoarece clauzele din S sunt formule inchise cu toate variabilele cuantificate universal, extinderea unei H−interpreta(ri partial generate este evident inutila daca ea falsifica cel putin o clauza din S.

Definitia 10. Fie S multime finita de clauze. Arborele T, binar, directionat, cu radacina si muchiile etichetate cu literali din B_H(S)U—B_H(S) este H−arbore semantic pentru S, daca indeplineste urmatoarele conditii:

i) muchiile divergente din orice varf au etichete perechi de literali complementari, ii) pentru orice varfn, nu exista duplicate ale literalilor si nici literali complementari in I,(n)

unde I este mul(n)timea etichetelor muchiilor componente ale drumului de la radacina la

n.

Observatie. Daca H_∞(S) este multime infinita atunci un H − arbore semantic pentru S poate eventual sa contina un numar infinit de varfuri.

Pentru orice varf n al unui arbore semantic, I(n) este o H − interpretare partiala. Daca

I(n) falsifica o clauza k S atunci pentru orice H−interpretare (H_∞(S),I*) care corespunde

unei multimi de literali A cu I(n) A, obtinem k^I* = F, deci (H∞ (S),I*) nu este model Herbrand pentru S.

Definitia 11. Fie S multime finita de clauze, Tun H − arbore semantic pentru S si n un varf al arborelui. Fie nn₀n₁n_k−1 drumul de la radacina la n in arborele T, r = n₀. Spunem ca n este varf de esec daca I falsific(n)a cel putin o clauza din S si pentru orice j, 0≤ j <k , nici o clauza din S nu este falsificata de I(n_j ).

Definitia 12. Fie S multime finita de clauze. Varful nal H − arborelui semantic T pentru S este un varf de inferenta daca n_v n₂ sunt varfuri de esec, unde n_v n₂ sunt succesorii lui n in T.

Definitia 13. H − arborele semantic T este un arbore inchis pentru S daca toate varfurile terminale ale lui T sunt varfuri de esec.

Definitia 14. H −arborele semantic T este un arbore complet pentru S daca pentru orice B_H(S) si pentru orice n varf al arborelui, sau II(n) ≠ sau exista n succesor al

lui n astfel incat δ, ()δ II(n*)≠

Din definitia 14. rezulta ca un H− arbore semantic complet explica toate H−interpreta(rile pentru multimea de clauze considerata. Deoarece prezenta simbolurilor functoriale impun H−arbori semantici infiniti, conditia de completitudine determina ca arborii semantici completi sa rezulte arbori infiniti.

Definitia 15. Fie T arbore (finit sau infinit). Multimea de varfuri D este o sectiune a arborelui T daca indeplineste urmatoarele conditii: i) pentru orice n varf al arborelui T exista Dn astfel incat n P_r*−_n sau n e P_r−n,

ii)        orice Dn1*,n₂* n1 *≠n₂*, n1 £P*_r_„₂ si n₂ £P_r*__v

unde P_n _−n este multimea varfurilor care compun drumul (daca exista) de la varful n₁ la varful n₂

in arborele T.

Din definitia 15. rezulta ca o sectiune D a unui arbore este o multime de varfuri cu proprietatea ii) si care este maximala in sensul relatiei de incluziune. De asemenea, este evident ca

pentru orice drum P maximal de origine radacina arborelui, DIP = 1.

Teorema 2. Multimea finita de clauze S este invalidabila daca si numai daca orice H − arbore semantic complet T pentru S contine un subarbore finit, semantic inchis T* astfel incat,

i)         T, T* au aceeasi radacina, ii) dT este sectiune a arborelui T unde dT este frontiera arborelui T* (multimea varfurilor

terminale in T ).

Corolar. (Teorema Skolem-Herbrand-Gödel). Multimea finita de clauze S este invalidabila daca si numai daca exista o multime S invalidabila de instantieri de baza ale clauzelor din S.

Stabilirea invalidabilitatii unei multimi de clauze S pe baza teoremei Skolem-Herbrand-Gödel, presupune generarea substitutiilor de baza, aplicarea lor clauzelor din S si testarea validabilitatii/invalidabilitatii multimii clauzelor astfel generate. Daca S este invalidabila, atunci exista garantia ca dupa un numar finit de iteratii va rezulta o multime invalidabila de instantieri de baza, dar daca S este validabila atunci acest proces continua indefinit. Deoarece clauzele sunt formule inchise cu toate variabilele cuantificate universal, cautarea unei multimi invalidabile de instantieri de baza revine in esenta la cautarea unui contra-exemplu (termeni Herbrand) intr-un spatiu (universul Herbrand) definit de structura clauzelor multimii S.

I.5. Demonstrarea automata bazata pe principiul rezolutiei pentru limbaje de prim ordin

Comparativ cu structurile de tip formula din limbajul calculului cu propozitii, formulele unui limbaj de prim ordin sunt structuri mult mai complexe, complexitatea rezultand in primul rand din prezenta substructurilor de tip termeni si a variabilelor. In cadrul acestei sectiuni va fi definit principiul rezolutiei ca unica regula de inferenta a unui sistem de demonstrare automata pentru limbaje de prim ordin.

In particular, pentru H = α₁,,α_n FORM₀, α FORM₀, deoarece H=α daca si

numai daca M(H) M()α si M(—α) = MM(α), rezulta ca H=α daca si numai daca

a,.) fi M -α = , deci daca si numai daca formula γ =    Aa₍. (-ia) este invalidabila.

Cu alte cuvinte, verificarea proprietatii H =α revine la verificarea invalidabilitatii unei reprezentari clauzale corespunzatoare formulei γ.

Pentru simplificarea notatiei, in continuare vom omite parantezarea conforma sintaxei limbajului in scrierea literalilor si a clauzelor. De exemplu, scrierea simplificata a clauzei ()()Px v Pfy v -Qx va fi PxvPJyv -Qx.

Definitia 1. Clauza kσ este factor al clauzei k daca σ este un cel mai general unificator (mgu) ce unifica cel putin doi literali din k.

Lema 1. Pentru orice clauza ksi SUBST, =kθ.

Definitia 2. Fie k_u k₂ clauze care au variabile comune. Clauzele k_u k₂ sunt rezolubile in raport cu perechea de literali ()L₁,L₂ daca k1L1, k₂L₂ si multimea este unificabila. Daca σ este un cel mai general unificator (mgu)pentru atunci clauza

rezbin()k₁ ,k₂ = (k₁σ L₁σ) v(k₂a L₂σ) este rezolventa binara a perechii de clauze (^, k₂).

Clauzele k₁, k₂ sunt clauze parentale pentru rezbin(k₁,k₂)

Definitia 3. Fie k_v k₂ clauze care au variabile comune. Orice rezolventa binara de unul din tipurile rezbin()k1,k2, rezbin()k₁σ₁,k₂, rezbin(k1,k2σ2), reabin(k₁σ₁,k₂σ₂) unde k₁σ₁, k₂σ₂sunt factori ai clauzelor k₁ respectiv k₂, este o rezolventa a perechii de clauze ()k1,k₂. Notam cu rez()k₁,k₂) o rezolventa a clauzelor k_v k₂.

Lema 2 (lema de liftare). Fie k_i, i = 1,2 instantieri ale clauzelor k_i, i = 1,2. Pentru orice k = rez(k`,k₂) rezolventa a perechii de clauze k, i = i exist=1,2a k = rez(k₁,k₂) astfel incat k este

instantiere a clauzei k.

Lema 3. Orice rezolventa este consecinta semantica a multimii clauzelor parentale. Definitia 4. Fie S multime finita de clauze. Secventa de clauze k₁,,k_n este o S − derivare

rezolutiva daca pentru fiecare ni = 1,, este indeplinita una din conditiile:

i) k^S;

ii) k_i este factor al unei clauze din S;

iii) exista j,l <i astfel incat k_i este rezolventa a perechii de clauze (kj ,kl).

S −derivarea rezolutiva k₁,,k_n este o S-respingereS− rezolutiva daca k._n =

Teorema 2. (Teorema de consistenta-completitudine a rezolutiei pentru limbaje de prim ordin) Multimea finita de clauze S este invalidabila daca si numai daca exista o S − respingere rezolutiva.

Rezultatul stabilit de teorema 2 constituie justificarea metodei rezolutive pentru verificarea validabilitatii/invalidabilitatii unei multimi finite de clauze.In principiu, metoda revine la cautarea unei S−respingeri rezolutive in spatiul extrem de complex al tuturor rezolventelor ce pot fi generate plecand de la clauzele multimii S. In functie de modul particular in care este organizat procesul de generare a rezolventelor rezulta o clasa de metode de demonstrare automata referita generic prin denumirea de metode rezolutive.

II. Programare logica

Scopul programarii logice consta in dezvoltarea unor algoritmi care sa permita derivarea unor concluzii din descrieri declarative. Deoarece descrierile declarative, numite programe logice, constau din multimi finite de formule logice, in esenta, sursa de baza in dezvoltarile de acest gen este reprezentata de teoria demonstrarii automate. Cu toate acestea, tranzitia de la demonstrarea automata la programarea logica necesita in primul rand obtinerea unor modalitati care sa asigure

eficienta sistemului deductiv respectiv. In general, acest lucru se realizeaza prin impunerea de restrictii suplimentare asupra limbajului formulelor procesate de un astfel de sistem. In cadrul acestui capitol vor fi prezentate semanticile declarative si procedurale corespunzatoare programelor definite, cel mai mic model Herbrand pentru un program definit, conceptul de raspuns corect, descrierea declarativa si corespondentul procedural al unui raspuns calculat pentru un program definit si un scop.

II. 1. Programe logice definite

In continuare vom considera problema modelarii cunostintelor exprimate prin intermediul frazelor unui sublimbaj particular al unui limbaj natural si anume asertiuni care exprima fapte pozitive si reguli.

Fiecare fraza a limbajului aserteaza ca o anumita relatie este adevarata pentru un numar de indivizi (fapt pozitiv) sau ca o anumita relatie rezulta adevarata pentru un grup de indivizi conditionat de indeplinirea unei secvente finite de relatii date (regula). Relatiile particulare in functie de care sunt exprimate frazele limbajului sunt exprimate ca atomi (literali pozitivi) in formalismul corespunzator limbajului de primul ordin utilizat pentru conceptualizare. Numele relatiei corespunde unui simbol predicational, aritatea simbolului exprimand numarul indivizilor la care se refera relatia considerata. Indivizii argumente ale relatiilor sunt reprezentati prin structuri simbolice din sortul TERM.

In cele ce urmeaza, pentru reprezentarea structurilor simbolice din multimea TERMU ATOM vom utiliza o sintaxa modificata, prin utilizarea unor simboluri de punctuatie paranteze si virgule, in modul urmator. Simbolurile non-logice utilizate pentru conceptualizare vor fi reprezentate astfel. Simbolurile din multimea CS U FS U PS sunt reprezentate prin secvente de caractere litere, cifre, sau simbolul '_', primul caracter fiind o litera format mic. Simbolurile din multimea V sunt reprezentate prin secvente de caractere litere, cifre, sau simbolul '_' , primul caracter fiind o litera format mare.

Structura simbolica ft1t_r(f) TERM U ATOM este reprezentata

Exemplul 1. Fie simbolurile predicationale fiu, nepot ambele de aritate 2. Relatiile 'X este fiu al lui Y', respectiv 'X este nepot al lui Y' sunt reprezentate prin atomii fiu(X, Y), respectiv nepot(X,Y).

Afirmatia 'Pentru orice X, Y, X este nepot al lui Y, daca exista Z, astfel incat X este fiu al lui Z si Z este fiu al lui Y' este reprezentata prin formula

a = VXVY(nepot(X,Y) <- Z(fiu(X,Z) a fiu(Z,Y)) Rezulta,

= VXVY{nepot ()()()X, Y v (-az(fiu(X, Z a fiuZ, Y = /XiY(nepot ()()()X, Y v /Z(-(fiu(X,Z) a fiuZ, Y = MXNYNZiriepot (X, Y) v {-{fiu(X, Z) a fiu(Z, Y)))) = MXNYNZiriepot (X, Y) <- {fiu(X, Z) a fiu(Z, Y))) = /XyYVZ{nepot ()()()X, Y v -fiuX, Z v -fiuZ, Y

Cu alte cuvinte, obtinem reprezentarea

α* = nepot (X, Y) ← (fiu(X, Z) a fiu(Z, Y))

semantic echivalenta cu α in care fiecare simbol de variabila care apare in atomii componenti este presupus a fi cuantificat universal.

Definitia 1. Limbajul clauzelor definite DefCl este definit prin

DefCl = ATOM U a₀ ← A₁ a a A_n n ≥ 1, A₀, A₁,, A_n ATOM

in care toate variabilele care apar in atomii componenti sunt implicit cuantificate universal in prefixul formulei.

O clauza definita atom se numeste clauza fapt sau clauza unitara. O clauza definita de tipul A₀ ← A₁ aaA_n se numeste clauza regula; A₀ este capul respectiv A^^.aA este corpul

clauzei.

Definitia 2. O multime finita de clauze definite se numeste program definit.

Observatie. Fie α* = A₀ ← A₁ AAA_n o clauza regula, X₁,,X_m variabilele care apar in atomii A₀,A₁,,A_n. Pentru α = VX_v..VX_m(A₀ ← A₁ AAA_n) rezulta,

a =VX_lVX_m ATOM si x₁,,X_n sunt variabilele care apar in atomii A,m_i i = Atomii A₁,,A_m sunt referiti ca subscopuri ale scopului G .

Daca G = VXjVX I -j AA_t 11 este o clauza scop, atunci

G =

Din punct de vedere intuitiv, semnificatia 'intrebarii' formulate prin scopul G corespunde negatiei afirmatiei ca exista valori (termeni) pentru variabilele X₁,,X_n, astfel incat relatiile exprimate prin atomii A_i, i = 1,,m sa devina simultan adevarate. Caracterul existential al intrebarii formulate printr-o clauza scop justifica tentativa sistemului de cautare a unui sistem de

(^m fi)

termeni t₁,,t_n, astfel incat formula rezultata din AA_i prin aplicarea substitutiei t₁X₁,,t_n X_n

sa fie adevarata in orice model al programului, adica sa construiasca o consecinta logica a programului, instantiere a conjunctiei tuturor subscopurilor clauzei scop. De asemenea

KA. v± NVX.VX M <_ Al

Aceasta reprezentare exprima ideea ca pentru un sistem arbitrar de valori (termeni) ale variabilelor X₁,,X_n, daca relatiile exprimate prin atomii A_i, i = 1,,m ar fi adevarate, atunci _L este adevarat, ceea ce este imposibil, cu alte cuvinte, nu exista un sistem de valori pentru variabile, astfel incat toate relatiile A_i, i = 1,,m sa fie adevarate.

In particular, ca si in cazul clauzelor definite, adoptand reprezentarea implicita a cuantificarilor universale, clauza scop G poate fi reprezentata ca disjunctie de literali negativi,

i

V()—Ai, respectiv _L<— AJ. in care toate variabilele care apar sunt cuantificate universal la

nivelul intregii formule.

(^m In programarea logica, pentru reprezentarea scopului definit _L <— A A_t este preferata

notatia

Definitia 2. Fie P program definit si G =← A₁,,A_m un scop definit. Orice substitutie pentru variabilele din G se numeste raspuns pentru PU. Substitutia raspuns θ este substitutie raspuns corect pentru P U , daca P =V((4 a a^JG).

Observatie. Pentru simplificare vom nota Va (respectiv 3a) orice forma prenex in care prefixul contine cate o cuantificare universala (respectiv existentiala) asupra fiecarei variabile care apare in formula α.

Observatie. Deoarece P =α, daca si numai daca P U este invalidabila, rezulta ca θ este substitutie raspuns corect pentru P U, daca si numai daca P j este

invalidabila.

Programele definite pot exprima numai cunostinte pozitive, in sensul ca atat faptele, cat si regulile specifica numai elementele unei structuri care sunt in anume relatii, si nu contin informatii relativ la situatiile in care relatiile nu sunt indeplinite. O consecinta imediata a acestei particularitati este aceea ca, utilizand limbajul programelor definite, nu este posibila obtinerea unor descrieri contradictorii (multime invalidabila de formule), deci orice program definit are cel putin un model. Din teorema 1.4.1 rezulta ca orice program definit admite cel putin un model Herbrand. Deoarece intr-o H−interpetare simbolurile functoriale si simbolurile constante au semnificatii predefinite, specificarea unei H − interpreta(ri revine la listarea relatiilor asociate fiecarui simbol predicational.

De exemplu, daca P este un simbol predicational de aritate n si M* = (H∞,I*) este o H−interpetare, atunci semnificatia P * a simbolului P este data de tuplele ()t₁,,t_n H_n pentru

care P¹*.

Observatie. Pentru simplificarea notatiei, daca M* =(H_∞(S),I*) este o H− interpetare arbitrara, convenim sa notam M* = (B_k)_k=1,₂, sirul de atomi de baza care o reprezinta (atomii de

baza validati de M* ).

Observatie. Stabilirea proprietatii ca o H−interpetare M*este model pentru o forma normala prenex cu toate cuantificarile de tip universal revine la verificarea daca toate instantierile de baza ale formulei sunt validate deM*.

In particular, pentru clauzele definite de tip regula

a = A₀ ←A₁,,A_m, m≥1

verificarea faptului ca M* este model pentru α revine la stabilirea proprietatii ca pentru orice substitutie de baza θ, daca Afi e M*, i = 1,,m atunci si A₀θ M*.

In plus, utilizand concluzia stabilita de urmatoarea teorema, va rezulta ca pentru un atom A si un program definit P , daca orice H − model pentru P este model si pentru A, atunci A este consecinta logica a programului definit P .

Teorema 1. Fie P program definit si G scop definit. Daca M = (D,I) este o

L − structura( model pentru PUG atunci M* = este H −model pentru

PUG.

Observatie. Rezultatul stabilit de teorema 1 se mentine daca P este o multime finita de clauze (nu neaparat definite), dar nu se mentine in cazul in care P este o multime arbitrara de formule inchise. In cazul general, este posibil ca o multime validabila de formule inchise sa nu admita model Herbrand.

Observatie. Daca P este un program definit, atunci M* =B_H(P) este un H− model pentru P .

Modelul B_H ()P) este insa destul de neinteresant, deoarece fiecare predicat este interpretat ca relatie pe domeniul tuturor termenilor de baza. Din punct de vedere intuitiv, deoarece clauzele unui program definit exprima numai informatie pozitiva, nu este de asteptat ca un H − model netrivial sa contina mai multi termeni de baza decat cei care rezulta din program.

Teorema 2. Daca P este un program definit si (Mi* )_i_I este o multime nevida de modele

Herbrandpentru P , atunci M* = IMi* este un model Herbrandpentru P .

i I

Observatie. Rezultatul stabilit de teorema 2 nu se mentine pentru programe care nu sunt definite.

Caracterizarea celui mai mic model Herbrand pentru un program definit dat P este stabilita in teorema urmatoare.

Teorema 3 (Emden, Kowalski). Cel mai mic model Herbrand al unui program definit P este multimea atomilor de baza care sunt consecinte logice ale programului

In continuare vor fi prezentate o caracterizare a celui mai mic model Herbrand al unui program definit P si o tehnica de constructie graduala a acestuia pe baza unei abordari bazate pe concepte si rezultate de punct fix.

Reamintim ca x₀ D este un punct fix al unei functii f : D →> D, daca f()x₀) = x₀ .

Suportul intuitiv al constructiei poate fi descris in modul urmator.

Evident toate instantierile de baza ale clauzelor fapt din P apartin oricarui H − model, deci

M1 a M*_p, unde M este multimea tuturor instantierilor de baza corespunzatoare clauzelor fapt din P . Daca A₀ ← A₁,,A_m ; m ≥ 1 este o clauza regula din P , atunci pentru orice H − model M* si orice θ substitutie de baza, daca A_iθ M*, i = 1,,m atunci A₀θ M*. Fiecare instantiere de baza a fiecarei clauze regula din P este utilizata in continuare pentru extinderea multimii M la M*₂ a MP*. Procesul continua atata timp cat sunt generate noi elemente, la fiecare j etapa a procesului, multimea M*j₊₁ rezultand prin adaugarea la multimea M*j a consecintelor semantice 'imediate' ale elementelor din M*j, rezultate pe baza programului P . Constructia revine la aplicarea iterata a transformarii

T B_H(P) _BH(P)

i p _: 2

numita operator consecinta semantica imediata.

Definitia 3. Fie C_H()P multimea instantierilor de baza ale clauzelor programului definit P . Pentru orice I B_H()P

T_P() I=_A0existaA₀ ←A₁,,A_m C_H(P) astfel incat I

Descrierea riguroasa a constructiei celui mai mic model Herbrand corespunzator unui program definit P presupune utilizarea unor concepte si rezultate relativ la structurile de ordine.

Definitia 4. Fie ()L,p o multime partial ordonata si L X . Elementul a L este cel mai mic majorantpentru X, daca indeplineste urmatoarele conditii: i)        pentru orice x X, xpa; ii) pentru orice a^′ care verifica conditia i), rezulta apa^′.

Evident, daca exista cel mai mic majorant pentru o multime X, el este unic si se noteaza cu lub(X).

Definitia 5. Fie ()L,p o multime partial ordonata si L X . Elementul b L este cel mai mare minorantpentru Xdaca indeplineste urmatoarele conditii: i)        pentru orice x X, bpx; ii) pentru orice b^′ care verifica conditia i), rezulta b^′pb.

Daca exista cel mai mare minorant pentru o multime X, atunci el este unic si se noteaza cu glb()X.

Definitia 6. Multimea partial ordonata (L,p) este o latice completa, daca pentru orice X L exista lub(X) si glb(X.

Observatie. Daca P este un program definit, atunci multimea H − interpreta(rilor 2 ^Heste o latice completa in raport cu relatia de incluziune, cu prim element si ultim element

'MP)-

Pentru orice familie ()Mi*iJ 2^bH(p), J

J i J

Definitia 7. Fie ()L,p latice completa si LX . Spunem ca multimea X este directionata, daca orice X F , F finita are o margine superioara inX, adica exista X y , astfel incat pentru orice x F, xpy.

Definitia 8. Fie ()L,p latice completa. Aplicatia T:L→L este monotona, daca pentru orice Lx,y , astfel incat xpy, rezulta T(x)pT(y).

Observatie. Deoarece pentru orice I ₁ I₂ c2 ^H( ', T_P(I ₁ T_P (I), rezulta ca T_P este operator monoton.

Definitia 9. Fie ()L,p latice completa. Aplicatia T:L→L este continua, daca pentru orice multime directionata X, T()lub()X − lub(T(X)).

Observatie. Orice aplicatie continua este monotona, dar nu si reciproc.

Intr-adevar, daca x,y L sunt astfel incat xpy, atunci lub()x,y= y, deci T()y=T()()()lubx,y=lubTx,Ty, ceea ce evident implica T(x)pT(y).

Definitia 10. Fie ()L,p latice completa si T: L →> L o aplicatie. Spunem ca a L este cel mai mic punct fix al aplicatiei T, daca aT(a) = a (a este punct fix) si pentru orice b L, astfel incat T(b) = b, rezulta apb.

Cel mai mic punct fix al aplicatiei T este notat lfp(T). Analog se defineste cel mai mare punct fix al aplicatiei T notat gfp()T.

Teorema 4 (Tarski). Daca (L,p) este latice completa si T:L→L aplicatie monotona, atunci exista lfp()T, gfp()T si

lfp()T=glb()

gfp)= lub()'

Teorema 5. Fie ()L,p latice completa si T :L →L aplicatie monotona. Daa a L este astfel incat apT()a, atunci exista a^′ punct fix al lui T, astfel incat apa′. Daca b L este astfel incat T()bpb, atunci exista b^′ punct fix al lui T, astfel incat b^′pb.

Reamintim ca primul ordinal, notat 0, este . Ordinalele finite sunt numerele intregi nenegative, si anume 1 = 2 = } = , 3 = ,}}= 0,1,2 si asa mai departe.

Primul ordinal infinit este multimea numerelor naturale ω.

Pe multimea ordinalilor se defineste relatia binara ' p ' prin, a α pβ daca α β. De exemplu, orice ordinal finit α, α p ω.

Evident ' p ' este o relatie de ordine partiala pe multimea ordinalilor. Daca α este ordinal, atunci succesorul lui α este α U notat α +1. Spunem ca ordinalul α este ordinal succesor, daca exista un ordinal β, astfel incat α = β +1. Daca α este succesorul ordinalului β, convenim sa notam β = α −1. Ordinalul α este ordinal limita, daca nu este succesorul unui alt ordinal. Evident cel mai mic ordinal limita diferit de 0 este ω.

Principiul inductiei transfinite: Fie P o proprietate definita pe multimea ordinalilor. Daca pentru orice ordinal β, presupunand ca P(γ) este adevarata pentru orice ordinal γ p β rezulta P()β adevarata, atunci P este adevarata pentru orice ordinal.

Puterile ordinale ale unei aplicatii monotone sunt definite astfel:

Definitia 11. Fie ()L,p o latice completa cu prim element _L si ultim element | . Daca
T :L→ L este o aplicatie monotona, atunci,
i) T;↑0 = ±;

ii) pentru orice ordinal α, T ↑ ()α +1 = t(t ↑ α); iii) daca α este ordinal limita, atunci T ↑ α = lub();

iv) T↓0 = |;

v) pentru orice ordinal α, T ↓ ()α +1 = T(T ↓ α);

vi) daca α este ordinal limita, atunci T ↓ α = glb(^).

O caracterizare interesanta a punctelor fixe gfp(T) si a lfp(T) corespunzatoare unei aplicatii monotone T:L→L, unde ()L,p este latice completa, rezulta in termenii puterilor ordinale ale aplicatiei T.

Teorema 6. Fie ()L,p latice completa si T^: L →> L o aplicatie monotona.

Pentru orice ordinal α, T↑αplfp(T) si exista β, astfel incat pentru orice β1, din βp
rezulta T^↑β1=lfp()T.

Pentru orice ordinal α, gfp()TpT ↓ α si exista γ, astfel incat pentru orice γ , din γpγ₁rezulta T ↓ γ1 = gfp()T.

Observatie. Cel mai mic ordinal α cu proprietatea ca T ↑ α = lfp(T) se numeste ordinalul inchidere al aplicatiei T.

O caracterizare a ordinalului inchidere in cazul aplicatiilor continue este stabilita de urmatoarea teorema.

Teorema 7 (Kleene). Daca (L,p) este latice completa si T:L→L este o aplicatie continua, atunci

Observatie. Conditiile din enuntul teoremei 7 nu sunt suficiente pentru ca sa asigure concluzia

In continuare rezultatele generale formulate de teoremele 4-7 vor fi utilizate in cazul

o /n

2 ^HV ', si al operatorului consecinta semantica imediata.

Teorema 8. Daca P este un program definit, atunci

T_P:2^B*^(PU2^B*^(P), data de definitia 3 este aplicatie continua.

Teorema 9. Daca P este un program definit atunci reaH − interpreta M* este model pentru P , daca si numai daca T_p(m *) M*.

Utilizand concluziile stabilite de teoremele precedente, obtinem caracterizarea de punct fix pentru cel mai mic model Herbrand al unui program definit.

Teorema 10 (Emden si Kowalski). Fie P un program definit. Atunci

M_P*=lfp()_TP = T_P

Teorema 11. Fie P program definit si G =← A₁,,A_m un scop definit. Daca θ este o substitutie raspuns pentru PUG, astfel incat (A₁ //A_mp nu contine variabile, atunci

urmatoarele afirmatii sunt echivalente:

(a)   θ este substitutie raspuns corect.

(b)   ()A₁ a a A_m θ este valida in orice H − model al programului P .

(c)    ()A₁ a a A_m θ este valida in M._P _*

II.3. Rezolutia - SLD

Dezvoltarile prezentate in cadrul acestei sectiuni vizeaza definirea semanticii procedurale corespunzatoare programelor definite. In acest scop este introdus un mecanism de deductie care constituie suportul inferential comun majoritatii sistemelor de programare logica.

Acest mecanism de inferenta se bazeaza pe o rafinare a principiului rezolutiei Robinson numita rezolutia- SLD (Selected-Linear-Definite) sau rezolutia-LUSH si a fost descrisa initial de catre Kowalski.

Corectitudinea concluziilor derivate dintr-un program logic pe baza principiului rezolutiei-SLD este garantata, cu alte cuvinte mecanismul de inferenta rezultat este logic consistent si permite definirea unei semantici operationale pentru programele definite.

Ideea generala pentru dezvoltarea unui mecanism de calcul corespunde unui rationament de tip reducere la absurd si anume pentru demonstrarea existentei unui sistem de valori care satisfac simultan o colectie de proprietati, se presupune contrariul, se elimina cuantificarile universale si se cauta generarea unui contraexemplu utilizand schema de inferenta modus ponens. Exemplul 2.3.1. Pentru descrierea cunostintelor :

A₁ = ' Orice parinte al unui nou-nascut este fericit';

A₂ = ' Orice persoana mama sau tata al unui copil este parinte';

A₃ = ' Maria este copilul nou-nascut al lui Ion'; consideram conceptualizarea CS = ()maria,ion, F =

PS = nou _ na(scut, pa(rinte, tata(, mama(, fericit

cu r()()fericit = rnou _ na(scut = 1, r(tata() = r(mama() = r(pa(rinte) = 2, semnificatiile intentionate pentru simbolurile predicationale considerate fiind respectiv,

nou _na(scat(X) X este nou nascut';

fericit(X) = 'X este fericit';

pa(rinte(X, Y) = 'X este parinte al lui Y';

tata((X,Y) = 'X este tatal lui Y';

mama((X,Y) = 'X este mama lui Y'.

Sistemul de cunostinte poate fi exprimat prin programul definit: P

fericit(X) ← pa(rinte(X, Y),nou_na(scut(Y)

pa(rinte(X, Y) ← tata((X, Y)

pa(rinte(X, Y) ← mama((X, Y)

tata((ion, maria); nou _ na(scut(maria).

Clauzele definite permit descrierea numai a cunostintelor pozitive si ca atare, de exemplu, nu este posibila specificarea persoanelor care nu sunt fericite. De asemenea, deoarece clauzele definite exprima cunostinte declarative, nici cunostintele interogative nu pot fi exprimate prin intermediul clauzelor program.

Formularea unei intrebari este realizata prin intermediul clauzelor scop.

Evident, din colectia de cunostinte considerata, rezulta ca raspunsul la intrebarea 'Cine este fericit ?' este 'ion'. Formularea intrebarii 'Cine este fericit ?' este realizata prin negatia ei si anume afirmatia 'Nimeni nu este fericit' formalizata VZ(—fericit(z)) si adresata programului prin clauza scop ← fericit()Z.

Astfel, derivarea raspunsului la intrebarea 'Cine este fericit ?' pe baza programului P revine la demonstrarea faptului ca VZ(—fericit(z)) este falsificata de orice model al programului (deci in particular falsificata si de modelul intentionat), ceea ce este echivalent cu demonstrarea proprietatii

Evident, (—>VZ(—fericit(z))) ≡ 3Zfericit(z), deci derivarea raspunsului la intrebarea considerata revine la demonstrarea proprietatii

P=3Zfericit(z).

Deoarece pentru orice formula α, P =α, daca si numai daca P U este invalidabila,

rezulta ca derivarea raspunsului la intrebarea considerata revine la demonstrarea invalidabilitatii multimii de formule P U , sau echivalent, la demonstrarea invalidabilitatii multimii PU ^Z(-,feridt(z))}.

Deoarece P = fericit(ion) rezulta P U invalidabila si ca atare rezultatul

unei scheme de verificare a invalidabilitatii ar conduce la confirmarea acestei proprietati fara sa identifice insa 'ion' ca raspuns la intrebarea 'Cine este fericit ?'.

Corectarea acestui neajuns este realizata prin formularea ca obiectiv al schemei de calcul determinarea unei substitutii θ cu proprietatea ca P =fericit(Z)θ sau echivalent

P U ()-fericit()Zθ sa fie invalidabila.

Pentru tratarea exemplului considerat, realizam urmatorul rationament:

Initial, consideram ipoteza G₀ = VZ(—fericit(z)) exprimand afirmatia 'Pentru orice Z, Z

nu este fericit'.

Inspecand cunostintele exprimate prin clauzele program, se identifica o clauza ce exprima conditia ca o persoana sa fie fericita si anume,

fericit(X) ← pa(rinte(X,Y),nou _na(scut(Y).

Deoarece pentru orice α, β formule (α → β) ≡ ((-β) →(-α)), clauza regula gasita este logic echivalenta cu

VX/Y(-fericit(x) X→ -(pa(rinte(X, Y) a nou _ na(scut(Y)).

Renotand X cu Z si eliminand cuantificarile universale, prin aplicarea regulei modus ponens cu G₀ obtinem,

—()pa(rinte(Z, Y) a nou _ na(scut(Y) sau echivalent

G₁ =← pa(rinte(Z, Y), nou _ na(scut(Y).

Cu alte cuvinte, dupa efectuarea primului pas de rationament, scopul initial G₀ a fost substituit cu un nou scop G1 valid in orice model al multimii P U , deci problema se reduce la verificarea proprietatii ca P U fo} este invalidabila.

Se observa ca G1 este logic echivalent cu

VZtfY((-parinte(Z, Y) v (-nou _ na(scut(Y)).

Pentru ca G1 sa fie falsificat de orice model al lui P este suficient sa fie gasita o persoana care este parintele unui copil nou-nascut. Ca atare, mai intai trebuie verificat daca din program rezulta ca exista persoane parinti.

Clauza regula pa(rinte(X, Y) ← tata((X, Y) este logic echivalenta cu

VXVY((-parinte(X, Y) → (-tata((X, Y)) si exprima o conditie pentru ca o persoana sa fie parinte si anume daca este tatal unui individ.

Procedand la renotarea variabilei X cu Z si la eliminarea cuantificarilor universale, prin aplicarea regulei modus ponens rezulta

()-tata((Z, Y))v (-nou _ na(scut(Y)) (implicit variabilele Z, Y sunt cuantificate universal), deci scopul G1 se substituie cu

G₂ =← tata((Z, Y), nou _ na(scut(Y).

Verificarea proprietatii ca G₂ este falsificat de orice model al lui P revine astfel la gasirea in cunostintele exprimate de program a unei persoane care sa fie tatal unui copil nou-nascut.

Repetand acelasi rationament si utilizand clauza tata((ion, maria), rezulta

()—nou _na(scut(maria), deci noul scop este

G3 =← nou _ na(scut(maria). Verificarea proprietatii ca G₃ este falsificat de orice model al lui P revine astfel la

verificarea daca din cunostintele formulate prin clauzele program rezulta ca proprietatea nou _na(scut(maria) este adevarata. Considerand clauza fapt nou _na(scut(maria) logic echivalenta cu

() nou _ na(scut(maria) →

rezulta in final clauza vida

Rationamentul efectuat a permis determinarea implicita a substitutiei θ = ionZ cu proprietatea ca P = fericit(Z)θ, termenul substituent 'ion' putand fi asimilat cu raspunsul la

intrebarea

'Cine este fericit?'

Termenul substituent 'ion' din substitutia rezultata θ = corespunde unui contraexemplu

pentru falsificarea scopului initial formulat.

Calculul initiat pentru respingerea scopului G₀ = VZ(—fericit(Z)) din exemplul 2.3.1. poate

fi reprezentat grafic prin schema din Figura 2.3.1, unde notatiile folosite au urmatoarea semnificatie:

A reprezinta: ← fericit(Z)

B reprezinta: fericit(X) ← pa(rinte(X,Y),nou_na(scut(Y)

C reprezinta: ← pa(rinte(Z,Y),nou _na(scut(Y), θ₁ =

D reprezinta: pa(rinte(X ,Y1) ← tata((X,Y1), θ₂ =

E reprezinta: ← tata((Z, Y), nou _ na(scut(Y)

F reprezinta: tata((ion,maria), θ₃ =

Greprezinta: ←nou_na(scut(maria)

H reprezinta: nou _ na(sut(maria)

A

B

i

C

D

i

<-

E

F

i

<r~

G

H

i

<r~

Figura 1.

Rezumand rationamentul efectuat pentru tratarea exemplului precedent, rezulta ca ideea consta in transformarea graduala a scopului initial, formulat prin intermediul unei clauze scop. Fiecare pas de transformare consta in selectarea unui atom al scopului curent, fie acesta P()s₁,,s_n , si a unei clauze din program de forma

P()t₁,,t_n←A₁,,A_m,m≥0, ATOM astfel incat

este multime unificabila. Convenim sa numim subscop curent atomul scopului curent selectat pentru aplicarea pasului de transformare.

Daca scopul curent este G = si θ este substitutie unificator pentru

P()()s₁,,s_n,Pt₁,,t_n, atunci scopul G se substituie cu G^′ = care

devine scop curent.

Dupa cum a fost ilustrat in exemplul 2.3.1, la fiecare pas k al calculului este calculata o substitutie unificator θ_k pentru subscopul curent si atomul cap al clauzei program selectate,

transformarea scopului curent in noul scop revenind in esenta la combinarea regulei de eliminare a cuantificarilor universale cu regula modus ponens. Rationamentul descris corespunde aplicarii principiului rezolutiei-SLD.

Calculul se termina daca scopul nou generat este clauza vida, ceea ce corespunde respingerii intregii secvente de scopuri intermediare, concluzia finala fiind invalidarea (respingerea) scopului initial, deci acceptarea negatiei acestuia.

( (^m Yi

Daca scopul inital este G = VX_v..X_n -. AA_t II, atunci concluzia finala corespunde

V

(m

acceptarii 3Xj3X I AA_t .

Daca procesul a constat in p etape, atunci invalidabilitatea scopului initial este demonstrata prin calculul instantierii

astfel incat P U - A i | ^ ° ° 8_p ^ este invalidabila, adica

P=AA₍ 8,unde 8 = θ₁ooθ_p.

Cu alte cuvinte, substitutia 9 corespunde unei modalitati de generare a unui contraexemplu pentru falsificarea scopului initial.

Observatie. Daca FV KA_t v$_v.8_p h* , atunci inchiderea universala a formulei

este consecinta semnatica a programului P . Observatii:

Procedura de calcul descrisa nu este determinista in sensul ca orice atom al scopului curent
poate fi selectat ca subscop curent si de asemenea pot exista mai multe clauze program cu
proprietatea ca atomul cap al clauzei este unificabil cu subscopul curent. Mai mult decat atat, in
general exista mai multe substitutii care sa unifice doi atomi, ceea ce sugereaza ideea ca este
posibila generarea mai multor contraexemple pentru acelasi scop initial. In general aplicarea
operatiei de unificare a atomului cap al unei clauze program cu atomul scop selectat este
realizata pe baza unui mgu al acestor atomi.

Din descrierea rationamentului efectuat rezulta ca este posibil ca subscopul curent sa nu fie
unificabil cu atomul cap al nici unei clauze program sau procesul de calcul initiat pentru
cautarea unei respingeri sa devina ciclic.

Deoarece variabilele care apar intr-un scop sunt cuantificate universal, global la nivelul
scopului, si pe de alta parte toate variabilele care apar in cele doua formule, subscopul curent si
clauza program selectata sunt cuantificate universal separat la nivelul fiecareia dintre ele, este
necesar ca multimile de variabile care apar in subscopul curent si clauza program selectata sa fie
disjuncte. Aceasta cerinta poate fi indeplinita intotdeauna prin renotarea variabilelor comune
subscopului curent si clauzei selectate sau prin renotarea variabilelor, astfel incat multimile de
variabile corespunzatoare clauzelor program si respectiv clauzei scop sa fie disjuncte.

Scopul curent poate eventual sa contina mai multi atomi unificabili cu atomul cap al unei
anumite clauze, ceea ce implica necesitatea postularii unui mecanism determinist pentru
alegerea subscopului curent. Un mecanism care realizeaza aceasta operatie este numit functie de
alegere sau regula de calcul.

Tehnica de rationament descrisa in tratarea exemplului 2.3.1 este in esenta metoda rezolutiei
Robinson adaptata pentru cazul particular al programelor definite si se numeste rezolutia-SLD
(Linear resolution with Selection function for Definite clauses ).

Formalizarea calculului descris corespunde regulei de inferenta din definitia 2.3.1. Definitia 1. Schema de inferenta SLD-rezolutia este

sau echivalent, utilizand notatiile din programarea logica,

V-(4 A A A_t__x A A_t A A_M A A A_m )V(5_O <r- B_x A A 5„ ) V—A_X A A A_i−1 A B1 A A B_n A A_i+1 A A A_m σ

unde

(i)        A₁,,A_m ATOM;

(ii) B₀ ← B₁,,B_n este o varianta a unei clauze program in care variabilele au fost renotate, astfel incat

fv(a 41 n (Wf A B_t 1U fv{b₀ ) j = 0

(iii) σ = mguA_i,B₀.

Definitia 2. Fie G =← A₁,,A_i=1,A_i,A_i+1,,A_m clauza scop si k = B₀ ← B₁,,B_n, clauza

definita.

k

Spunem ca G^′ deriva din G utilizand k si σ, notat G~ →G^′, daca

G^′=←(A₁,,A_i−1,B₁,,B_n,A_i+1,,A_m)σ, unde σ = mgu(A_i,B₀).

Spunem ca G^′ deriva nerestrictionat din G utilizand k si σ, daca
G^′ =← ()A₁,, A_i−1,B₁,,B_n, Ai+₁,, A_mθ, unde θ este substitutie unificator pentru A_i,B₀.

k Observatie. Daca G ~ →G^′, atunci G^′ este o rezolventa a clauzelor G si k.

Definitia 3. Fie G₀ scop definit, P program definit si R o regula de calcul. Secventa finita sau infinita de scopuri ()G_i )._=o _l este o SLD − derivare a lui G₀ pe baza programului P si a

regulei R, daca pentru orice i≥0 exista k_i clauza a programului P , astfel incat G_i ~ →Gi′₊₁ prin selectarea atomului subscop conform regulei R si k[ este o varianta a clauzei k cu variabilele

renotate, astfel incat este indeplinita cerinta (ii) din definitia 2.3.1.

^ko Vi

Definitia 4. Daca G₀ ~>G_V..—→G_n este o SLD−derivare finita si σ₀,,σ_n−1 este

secventa de substitutii mgu rezultate in derivare, atunci

σ0_o°σ_n−1 dacan≥1
[e daca n = 0

se numeste substitutia calculata de derivare.

Definitia 5. Fie G scop definit si P program definit si R o regula de calcul.

h        SLD − derivarea finita G₀ ~ →G₁ ~ →Gn este o SLD — respingereSLD− de lungime n pentru P U,

daca G_n =

'B-l , ..

Spunem ca G₀ ~ →G₁ ~ →G_n = este SLD - respingereSLD− nerestrictionata pentru P U,

daca G_i+1 deriva nerestrictionat din G_i, i. = 0,,n−1

Definitia 6. Daca σ este substitutia calculata de derivare de o SLD - respingereSLD− pentru P U G , substitutia rezultata prin restrictionarea substitutiei σ la variabilele din G se numeste substitutia raspuns calculat pentru G .

Concluzia formulata de urmatoarea teorema stabileste ca utilizarea substitutiilor mgu in construirea SLD − deriva(rilor nu determina modificari din punctul de vedere al capacitatii de respingere comparativ cu metoda bazata pe derivari nerestrictionate.

Teorema 1. Fie P program definit, R regula de calcul si G scop definit. Daca exista o SLD − respingere nerestrictionata de lungime n pentru PU, atunci exista si o SLD − respingere de aceeasi lungime. Daca (9,)_i=0 _n__x, ^ai)_i=0 „_i sunt substitutiile unificator respectiv substitutiile unificator mgu corespunzatoare celor doua respingeri, atunci exista X SUBST, astfel incat θ₀ o o 9^ = o o σ_n−₁λ.

Apare in mod firesc intrebarea in ce masura existenta unei SLD − respingeri este influentata de aplicarea unei substitutii clauzei scop. Concluzia data de teorema urmatoare stabileste raspunsul la aceasta intrebare si, mai mult decat atat, stabileste si corespondenta intre secventele de substitutii mgu corespunzatoare respingerilor unui scop si a transformarii lui rezultata prin aplicarea unei substitutii. Tipul de concluzie stabilita de teorema corespunde ideii de 'ridicare' in spatiul substitutiilor si este frecvent referit prin atributul 'liftare'.

Teorema 2. Fie P program definit, R regula de calcul, G scop definit si θ SUBST. Daca exista o o — respingereSLD− de lungime n pentru P U , atunci exista si o SLD − respingere pentru PUG de aceeasi lungime. Daca (9,)_i=0 _n__x, (o,)_i=0 _n- ^suntsecventele de substitutii mgu corespunzatoare lui PU, respectiv PUG, atunci exista X SUBST, astfel incat θ o θ₀ o o 9^ = σ₀ o o σ_n−1 o λ.

Exemplul 2. Fie programul P si clauza scop G₀ din exemplul 1. Pentru regula de calcul R

care selecteaza primul atom din secventa de atomi corespunzatoare scopului curent obtinem SLD − respingerea

G₀ =← fericit(Z)

k₀ = fericit()X₀ ← pa (rinte(X₀, Y₀), nou _ na(scut(Y₀)

= mgufericit(Z), fericit(X₀) = {ZX₀

G₁ = pa(rinte()Z, Y₀ , nou _ na(scut(Y₀)

k₁ = pa(rinte()X₁, Y 1 ← tata((X₁, Y₁)

σ₁ = mgupa(rinte()Z, Y₀ , pa(rinte(X₁ ,Y₁)= {ZX₁, Y₀ Y

G₂ = tata(()Z, Y₀ , nou _ na(scut(Y₀)

k₂ = tata((ion, maria)

a₂ = mgutata(()Z ,Y₀,tata((ion,maria) =

G₃ = nou _na(scut(maria)

k₃ = nou _na(scut(maria)

Substitutia calculata de derivare este

a = σ₀σ₁σ₂σ₃ =

Substitutia raspuns calculat pentru G₀ este

Observatie. In general pentru un program definit si un scop definit exista mai multe derivari-SLD. In conditiile in care exista cel putin o SLD − respingere, anumite derivari-SLD maximale pot fi de lungime finita fara sa fie respingeri sau pot fi de lungimi infinite.

Definitia 7. Fie P program definit. Multimea de succes a programului P este aA B_H () P, exista o respingere SLD pentru P U .

Observatie. Multimea de succes a unui program definit este analogul procedural al celui mai mic model Herbrand. Analogul procedural al conceptului de substitutie raspuns corect este conceptul de substitutie raspuns calculat.

II.4. Consistenta si completitudinea rezolutiei SLD

Din prezentarea efectuata in sectiunea precedenta, a rezultat ca generarea unei SLD − respingeri pentru P UG determina si obtinerea unei substitutii raspuns calculat care corespunde unui raspuns la intrebarea exprimata prin scopul definit G obtinut pe baza programului definit P si a regulei de calcul R . In cazul in care nu exista o SLD−respingere pentru P U , substitutia raspuns calculat este asimilata cu raspunsul 'nu', respectiv in cazul in care substitutia raspuns calculat este substitutia vida, raspunsul este asimiliat cu 'da'.

Corespondenta ()()P,G,R,σ, unde σ este o substitutie raspuns calculat, corespunde unui tip de regula de inferenta si in consecinta devine necesara stabilirea unor concluzii relativ la

proprietatile de consistenta si completitudine. Proprietatea de consistenta este esentiala si garanteaza corectitudinea concluziilor derivate de catre sistem in sensul ca aceste concluzii sunt consecinte logice ale programului. Cu alte cuvinte, daca pentru o regula de inferenta este demonstrata proprietatea de consistenta, atunci exista garantia ca orice concluzie derivata pe baza ei este adevarata in orice model al programului, deci in particular si in modelul intentionat.

Teorema 1. (Teorema de consistenta a rezolutiei SLD, Clark, 1979) Fie P program definit si R o regula de calcul. Daca σ este o substitutie raspuns calculat pentru scopul definit G =← A₁,,A_m, atunci

(^m ^
^PI^=VI^A,4 1°

Corolar 1. Daca exista o SLD — respingereSLD− pentru P U, unde P este program definit si G scop definit, atunci P U G este invalidabila.

Corolar 2. Daca S_H ()P) este multimea de succes a programului definit P , atunci

Teorema 2 (Apt, van Emden). Fie P program definit si G =← A₁,,A_m scop definit. Daca exist a SLD o respingereSLD− de lungime n pentru P U si σ₀,σ₁,,σ_n−1 este secventa substitutiilor mgu corespunzatoare respingerii, σ = ° σ₁ ° ° σ_n−1, atunci

Problema stabilirii daca orice consecinta logica a unui scop dat poate fi demonstrata pe baza rezolutiei-SLD corespunde stabilirii proprietatii de completitudine a acestei reguli de inferenta.

Demonstrarea unui rezultat de tip completitudine pentru rezolutia-SLD necesita stabilirea in prealabil a unor rezultate suplimentare, fiecare exprimand, intr-un anumit sens, tot o concluzie de tip completitudine.

Teorema 3 (Apt, van Emden). Multimea de succes corespunzatoare unui program definit este cel mai mic model Herbrand al programului.

Teorema 4 (Hill, 1974). Fie P program definit si G scop definit. Daca P U este invalidabila, atunci exista o SLD — respingereSLD− pentru P U .

Corolar 3. Daca P este program definit si G scop definit, atunci P UG este invalidabila, daca si numai daca exista o SLD − respingere pentru P U .

Concluzia este o consecinta imediata a rezultatelor stabilite de corolarul 1 si teorema 4.

In continuare vom demonstra ca orice substitutie raspuns corect (definitia 2, sucapitolul II.2.) rezulta ca substitutie raspuns calculat pentru o SLD − respingere (definitia 6, subcapitolul II.3.).

Teorema 5. Daca P este program definit si A ATOM, astfel incat P =/A, atunci exista

o SLD - respingereSLD− pentru P U ← A pentru care substitutia raspuns calculat sa fie ε.

Teorema 6 (Completitudinea rezolutiei SLD, Clark,1979). Fie P program definit, R

regula de calcul si G =← A₁,,A_m scop definit. Daca P =V AA_l 9, θ SUB ST, atunci exista o

I m

SLD − respingere pentru P UG calculata pe baza regulei R si AA₍ 9 este o instantiere

i=1

pentru A A_t x, unde τ este substitutia raspuns calculat de respingere.

i=1

Problema asupra careia vom obtine concluzii in continuare este stabilirea corelatiilor intre demonstrabilitatea pe baza rezolutiei-SLD si diferitele reguli de calcul particulare.

Evident, utilizarea unei reguli de calcul in construirea SLD − deriva(rilor revine la impunerea unui anumit tip de restrictie in sensul ca, daca acelasi scop revine de mai multe ori in derivare, atunci regula de calcul va identifica de fiecare data acelasi atom al scopului pentru aplicarea pasului de rezolutie.

Cu alte cuvinte, data fiind o regula de calcul particulara R , exista SLD − deriva(ri care nu sunt SLD − deriva(ri calculate pe baza regulei R .

Definitia 1. Fie FO_RM α ,β TERMU. Spunem ca α este o varianta a lui β, daca exista SUBST, astfel incat α = βθ si β = αλ.

Evident, daca α este o varianta a lui β, atunci si β este o varianta a lui α.

Definitia 2. Fie P program definit, G scop definit si R regula de calcul. Substitutia σ este o substitutie R− ra(spuns calculat pentru P U, daca exista o SLD − respingere pentru P U G calculata pe baza regulei R pentru care σ este substitutie raspuns calculat.

Definitia 3. Fie P program definit. Daca R este o regula de calcul, atunci R − multimea de succes a programului P este multimea atomilor de baza A cu proprietatea ca exista SLD − respingere pentru P U ← A calculata pe baza regulei R .

Definitia 4. Fie k = A← A₁,,A_m, m ≥ 0 o clauza definita; cazul m = 0 prin conventie corespunde clauzei fapt k = A. Notam H(k) = A si cu B(k) secventa ordonata a subscopurilor din corpul clauzei k, B{k) = A₁,,A_m.

Teorema 7. Fie P program definit si G scop definit. Presupunem ca

^k h Vi ^kq ^kq+1 ^kn−2 ^kn− 1

G =G₀ ~->G, ~->~->G, ~^G_q+l ~->~->G_I__I ~->G„ = J_

este o SLD — respingereSLD− a scopului pentru P U si fie σ₀,,σ_n−1 secventa de substitutii mgu corespunzatoare etapelor derivarii, σ substitutia raspuns calculat.

Daca A_i, A_j sunt subscopurile curente la pasii de derivare (q − 1) respectiv q,

G_q+1 =←(A₁,,A_i−1,B(k_q−1),,A_j−1,B(k_q),,A_m)σ_q−1 o_σq,

atunci exista o SLD − respingere pentru P U , astfel incat A_j este subscopulselectat in G_q−1 si A este subscopul selectat in iG_q. Daca τ este substitutia raspuns calculat de aceasta respingere,

atunci Gσ este o varianta pentru Gτ

Corolar 4. Fie P program definit si G scop definit. Presupunem ca exista o SLD − respingere pentru P UG pentru care substitutia raspuns calculat este σ. Pentru orice regula de calcul R, exista o SLD − respingere pentru P U pe baza regulei R si, daca σ^′ este substitutia R − ra(spuns calculat, atunci Gσ^′ este o varianta a lui Gσ.

Corolar 5. Fie P program definit. Pentru orice R regula de calcul, R − multimea de succes a programului P coincide cu cel mai mic model Herbrand al programului.

Corolar 6. Fie P program definit, G scop definit si R regula de calcul. Daca P U este invalidabila, atunci exista o SLD - respingereSLD− pentru P U calculata pe baza regulei de calcul R

Corolar 7 (Versiunea tare a teoremei de completitudine a SLD − rezolutiei). Fie P program definit, G scop definit si R regula de calcul. Daca θ este o substitutie raspuns corect pentru PUG, atunci exista σ substitutie R− ra(spuns calculat pentru PUG si exista X SUBST, astfel incat θ = σ o λ.

II.5. Proceduri de respingere - SLD

In cadrul acestei sectiuni vor fi prezentate strategii pe care un sistem de programare logica le poate adopta ca baza pentru dezvoltarea unor proceduri de cautare a SLD − respingerilor.

In cazul unui program definit P si al unui scop definit G ,astfel incat P U este invalidabila, concluziile stabilite de teoremele prezentate in sectiunile precedente garanteaza existenta unei intregi clase de SLD − respingeri pentru P U, precum si posibilitatea generarii

de 'contraexemple' reprezentate de substitutiile raspuns calculat, dar nu ofera si modalitati constructive pentru determinarea cel putin a unora dintre aceste derivari.

De exemplu, rezultatul stabilit de teorema 2.4.6 care poate fi reformulat prin: 'Daca P este program definit, R regula de calcul si G scop definit, atunci pentru orice substitutie raspuns corect θ pentru P U G exista o substitutie raspuns calculat σ pentru P U G, astfel incat exista X SUBST, si θ = σ ° λ conduce la concluzia ca pentru orice substitutie raspuns corect exista cel putin o SLD − respingere capabila sa calculeze un raspuns mai general, dar nu rezulta si cum putem proceda pentru a obtine efectiv o astfel de respingere.

Asa dupa cum va rezulta in cadrul acestei sectiuni, o SLD − respingere corespunde unui drum complet in SLD − arborele corespunzator unui scop definit si unei reguli de calcul date, deci, o tentativa pentru determinarea unei SLD − respingeri ar putea consta in initierea unei cautari sistematice a unui SLD−arbore. Pentru majoritatea sistemelor PROLOG existente, ordinea clauzelor in cadrul programului este esentiala, ceea ce revine la ordonarea multimilor de muchii divergente fiecarui nod al arborelui.

Cautarea unei SLD − respingeri revine la traversarea 'in adancime' (depth-first), conform acestei ordonari, a unui SLD − arbore, conditia de terminare fiind atingerea unui varf etichetat cu clauza vida. In situatia in care directia de cautare curenta 'esueaza', in sensul ca este atins un varf terminal fara sa fie generat scopul vid, corectia operata asupra directiei de cautare curente este realizata prin revenirea la varful parental varfului curent si explorarea unei noi alternative (invocarea mecanismului de back-tracking).

In cazul unui SLD − arbore finit, strategia descrisa este completa in sensul ca determina o SLD − respingere intr-un numar finit de etape, dar daca SLD − arborele este infinit, atunci nu mai este garantata proprietatea de completitudine, fiind posibil ca procesul de cautare sa continue indefinit.

Optiunea pentru o strategie de cautare 'in latime' (breadth-first) permite evitarea acestei situatii, dar in schimb creeaza multiple dificultati de implementare, in special deoarece eficienta sistemului rezultat depinde esential de solutia gasita pentru gestionarea spatiului necesar stocarii informatiei intermediare generate pe durata evolutiei procesului de cautare.

Definitia 1. Fie P este program definit, R regula de calcul si G scop definit. Arborele T directionat, cu radacina si varfurile etichetate cu clauze scop este SLD −arbore pentru P U calculat pe baza regulei R, daca sunt indeplinite urmatoarele conditii:

Notand cu (p(«) eticheta varfului n,

(t>(r) = G, unde r este radacina arborelui,

Daca cp(ra) = , atunci od(n) = 0,

Daca cp(ra) =← A₁,,A_m,,A_k, k≥1 si A este atomul semlectat de regula R, atunci
od(n) = s, unde s este numarul clauzelor program cu proprietatea ca atomul cap al clauzei
este unificabil cu A_m. Notand cu n₁,,n_s succesorii varfului n, pentru fiecare n_i, i = 1,,s,
daca A ← B₁,,B_p, p≥0 este clauza program corespunzatoare varfului n_i, atunci

unde θ = mguA,A_m.

Spunem ca SLD − arborele T este arbore de demonstratie sau arbore complet pentru P U G , daca eticheta oricarui varf terminal este clauza vida.

Definitia 2. Fie P program definit, R regula de calcul, G scop definit si T SLD − arbore pentru P U G calculat pe baza regulei R .

Convenim sa notam cu T_n _−n drumul de la varful n₁ la varful n₂ in arborele T si cu r varful

radacina. Spunem ca T_r−n este drum de succes, daca cp(ra) n . Dac)=a od(n) = 0 si cp(ra) ) _≠

atunci T_r−n este drum de esec.

Observatie. Daca T este SLD−arbore pentru P U calculat pe baza unei reguli R, atunci pentru orice n varf al arborelui, T_r−n corespunde unei SLD−deriva(ri pentru P U calculate pe baza regulei R .

Daca T_r−n este drum de succes, atunci SLD − derivarea corespunzatoare este o

SLD − respingere pentru P UG, respectiv daca T_r−n este drum de esec, atunci SLD − derivarea corespunzatoare nu este SLD − respingere pentru P U .

Fiecare drum al unui SLD − arbore corespunde unei anumite ordini in care sunt considerate clauzele programului pastrand aceeasi regula de calcul.

Daca SLD−arborele T este arbore de demonstratie pentru P U, atunci este garantata generarea unei SLD − respingeri pentru P U calculata pe baza regulei R indiferent de ordinea in care sunt considerate clauzele programului. Cu alte cuvinte, existenta unui arbore de demonstratie pentru P U G exprima o proprietate de independenta a demonstratiei fata de ordinea clauzelor in program.

Generarea unui arbore SLD−arbore pentru P U poate fi realizata prin extinderea graduala a arborelui curent, astfel incat sa fie indeplinite cerintele din definitia 2.5.1.

Initial, arborele curent este T = (V(T),E(T)) unde V(T) = , E(T) = si cp(r) = G .

Extinderea arborelui curent T este efectuata astfel:

Se alege n ∂T, astfel incat cp(ra) ≠ si atomul selectat conform regulei R din

q>(n) =← A₁,,Aj₋₁,A_j,A_j+1,,A_m este unificabil cu atomul cap al cel putin unei clauze program. Presupunem ca Aj este atomul selectat. Fie s numarul clauzelor program cu proprietatea ca Aj este unificabil cu atomul cap al clauzei.

Genereaza s noi varfuri n₁,,n_s;

V(T)←V(T)U E(T)←E(T)U

Etichetarea varfurilor n₁,,n_s: pentru fiecare i, 11 ≤ i ≤ s,

(3.1.) Fie k_i =B ←B 1,,B_p clauza program corespunzatoare varfului n_i. Genereaza ki′ =B ′← B1′,,B^′_p o varianta a clauzei k_i cu variabilele renotate astfel incat multimea variabilelor care apar in (p(«) sa fie disjuncta de multimea variabilelor ce apar in k.

(3.2.) Calculeaza θ = mguA_J,B′.

(3.3.) cpk)=^Uv..,^_₁₅A'v₅5;,^₊₁,,^)e.

Constructia descrisa este ilustrata in urmatorul exemplu. Exemplu. Fie programul P :

k₂=P(a,f(a)) k₃=P(f(b),b)

k₄=P(f(b),b),

clauza scop G =← P(X,Y),Q(X,Y) si regula de calcul R care selecteaza primul atom din secventa de atomi ce compun clauza scop, a,b CS.

Aplicand metoda descrisa, rezulta: P1. T = ()r, , cp(r) =←P(X,Y),Q(X,Y), ∂T = .

P2.Pentru atomul selectat P(X,Y), s = 3; genereaza noile varfuri n₁,n₂,n₃; n_i asociat clauzei k_i, i = 1,2,3

V(T) = r,n₁,n₂,n₃; E(T) = ; ∂T = ;

k[ =P()()X₁,Y₁←PX₁,Z₁,Q(Z₁,Y₁), θ₁=mgu=XX₁,YY₁,

k₂′ =k₂ =P()a,f(a), θ₂ =mgu=aX,f(a)Y,

(p(«₂)=^e(a,/(fl));

k₃′=k₃ =P()f(b),b, θ₃ =mgu=f(b)X,bY,

P3. Pentru alegerea n₃ ∂T, s = 1; genereaza varful n₄

V(T)←V(T)Un₄, E(T)←E(T)U, ∂T =

k =k₄ =Q()f(b),b, θ₄=mgu = ε, cp(«₄) = .

P4. Unicul varf din ∂T care permite extinderea arborelui este n₁. Atomul selectat din cp(«j) este P()X,Z₁ pentru care s = 3; clauzele cu al caror atom cap este unificabil P(X,Z₁), sunt k_i, i = 1,2,3 . Genereaza noile varfuri n₅,n₆,n₇,

V(T)←V(T)Un₅,n₆,_n7, E(T)
∂T = n₂,n₄,n₅,n₆,n7;

Calculul etichetelor varfurilor nou generate:

k1′ = P()X₂,Y₂←P(X₂,Z₂),Q(Z₂,Y₂),

θ₅=mguP()X,Z₁,P(X₂,Y₂)=,

()()n₅=← PX,Z₂,Q(Z₂,Z₁),Q(Z₁,Y),Q(X,Y);

k₂′=k₂=P()a,f(a),

θ₆ = mguP()X,Z₁,P(a,f(a))=,

)()n₆=←Qf(a),Y,Q(a,Y);

k₃′=k₃=P()f(b),b,

θ₇ = mguP()X,Z₁,P(f(b),b)=,

P5.Unicul varf din ∂T care permite extinderea arborelui este n₅, scopul selectat este P()X,Z₂. Este evident ca prin aplicarea metodei varfului n₅ rezulta noile varfuri n₈,n₉,n₁₀ asociate respectiv clauzelor k₁,k₂,k₃. Situatia este similara cazului P4, deci extinderea in continuare in directia r−n₁−n₅−n₈ va conduce la o derivare infinita, deci

SLD− arborele va contine cel putin un drum infinit. Deoarece cp(«₄)= , drumul T_r−n = ()r, n₃, n₄) este drum de succes si corespunde SLD − respingerii:

k0         k 1

G₀=G =←

k - k σ₀=θ₃=f(b)X,bY

KK

Substitutia calculata coincide cu substitutia raspuns calculat σ = σ₀oσ₁ = f(b)X,bY.

Teorema 1. Fie P program definit, G scop definit si R regula de calcul. Daca P U este invalidabila, atunci SLD −arborele pentru P U calculat pe baza regulei R contine cel putin un drum de succes.

Teorema 2. Daca P este program definit, G scop definit si R regula de calcul, atunci pentru orice θ substitutie raspuns corect pentru P U exista un drum de succes, astfel incat, daca σ este substitutia R− ra(spuns calculat pentru PU corespunzatoare drumului de succes, atunci exista λ SUBST si

Definitia 3. Numim regula de cautare o strategie pentru identificarea drumurilor de succes dintr-un SLD − arbore. Numim aSLD − procedur( de respingere o pereche compusa dintr-o regula de calcul si o regula de cautare.

Majoritatea sistemelor PROLOG utilizeaza regula de calcul care selecteaza cel mai din stanga atom al scopului curent si regula de cautare DF (depth-first). Avantajul utilizarii acestei reguli de calcul consta in faptul ca procesul de cautare poate fi implementat prin utilizarea unei stive pentru retinerea scopurilor intermediare. Daca atomul selectat din scopul varf al stivei este unificabil cu atomul cap al unei clauze program, atunci clauza rezolventa este inclusa in stiva. In cazul cand nu mai exista clauze program, astfel incat atomul selectat sa fie unificabil cu atomul cap al clauzei, se procedeaza la eliminarea scopului varf al stivei si procesul continua prin cautarea pentru noul varf al stivei a unei clauze program neutilizate inca in tratarea acestui scop. Cautarea DF revine la specificarea unei anumite relatii de ordine in tratarea clauzelor program. Pentru majoritatea sistemelor PROLOG ordinea in care sunt tratate clauzele programului ramane nemodificata pe durata cautarii, aceasta restrictie permitand implementari simple si eficiente. Posibilitatea existentei drumurilor infinite intr-un SLD − arbore impune complexificarea procesului de cautare prin adaugarea unei componente BF (breadth-first), ceea ce in general determina degradarea eficientei implementarii.

Descrierea semanticii procedurale a unui sistem PROLOG revine la specificarea modului in care sistemul opereaza pentru generarea raspunsurilor pentru o intrebare adresata prin lista atomilor ce compun clauza scop G . Un raspuns pentru G pe baza programului P corespunde unei substitutii raspuns calculat pentru P U. In cazul in care P U nu este invalidabila, in SLD−arborele generat nu exista drum de succes si calculul se incheie cu raspunsul 'no'. Daca P U G este invalidabila, atunci in SLD − arbore exista cel putin un drum de succes fiecare drum de succes corespunde cate unei SLD − respingeri

Rezolvarea unui scop G pe baza unui program logic P de catre un sistem PROLOG revine la generare a substitutiilor raspuns calculat corespunzatoare SLD − respingerilor din SLD − arborele pentru P U G, fiecare substitutie raspuns calculat fiind asimilata cu un raspuns la intrebarea G .

Calculul efectuat de un sistem PROLOG pentru rezolvarea unui scop G este descris in procedura executa.

Argumente de intrare:

Program: lista de clauze definite ListaScopuri: lista de scopuri Argumente de iesire:

Succes: variabila booleana, Succes=true, daca si numai daca ListaScopuri

este vida pentru Program. Variabile locale:

Scop: clauza scop RestScopuri: lista de clauze scop Rezolvat: variabila booleana Rezultat: variabila booleana Substitutie: substitutie Functii auxiliare:

vid (L): returneaza true daca si numai daca lista L este vida; CapLista (L): returneaza primul element al listei L; RestLista (L) : returneaza lista rezultata din lista L prin eliminarea primei

componente;

Lipeste (L1,L2): returneaz lista rezultata prin adaugarea componentelor listei L2 dupa ultima componenta din lista L1 (calculeaza rezultatul concatenarii listei L$ cu lista$L$).

Unifica (TI,HJlezultatJSubstitutie) : aplica algoritmul de unificare Robinson argumentelor T1, T2; daca multimea este unificabila, atunciRezultat=true siS^ubstⁱtutⁱe=mgu; AplicaSubstitutie (Substitutie,ListaScopuri) : substituie variabilele din lista de scopuri ListaScopuri cu termenii substituenti corespunzatori din substitutia Substitutie.

procedure executa (Program ,ListaScopuri,Succes) if vid (ListaScopuri) then Succes:=true else

Scop:= CapLista (ListaScopuri);

RestScopuri:=RestLista (ListaScopuri);

Rezolvat:=false

while not (Rezolvat) do

Fie A← B₁,,B_n urmatoarea clauza din program si A^′ ← B1′,,B_n′ o

varianta cu variabilele renotate; Unifica (Scop, A^′ ,Rezultat,Substitutie)_;If Rezultat then

NoileScopuri:=Lipeste ([B[,,B'_n ]JlestScopuri);

NoileScopuri:= AplicaSubstitutie (Substitutie ,NoileScopuri); executa (Program ,NoileScopuri ,Rezultat)

endif endwhile Succes:=Rezultat;

endif; endprocedure;

BIBLIOGRAFIE

State, L. (2004) - Introducere in programarea logica, Editura Fundatiei Romania de Maine,

State, L. (1988) - Elemente de logica matematica si demonstrarea automata a teoremelor,
Tipografia Universitatii Bucuresti, 1989

Cloksin, W. & Mellish, C. (1994) - Programming in PROLOG, Springer Verlag, 4th Edition

Genesereth, M.R. & Nilsson, N.J. (1987) - Logical Foundation of Artificial Intelligence, Los
Altos, CA: Morgan Kaufmann

Gentzen, G. (1969) - The Collected Papers of Gerhard Gentzen, Ed. Szabo, M.E., North
Holland

Lloyd, J.W. (1987) - Foundations of Logic Programming, Springer Verlag

Loveland, D.W. (1978) - Automated Theorem Proving: A Logical Basis, North Holland

Nilsson, U. & Maluszynski, J. (2000) - Logic, Programming and PROLOG, Jogh Wiley & Sons

Sterling, L. & Shapiro, E. (1994) - The Art of PROLOG, MIT Press

Document Info

Accesari: 1004
Apreciat:

Comenteaza documentul:
Nu esti inregistrat
Trebuie sa fii utilizator inregistrat pentru a putea comenta

Creaza cont nou

A fost util?
Daca documentul a fost util si crezi ca merita
sa adaugi un link catre el la tine in site

Copiaza codul:
in pagina web a site-ului tau.

<a href="https://www.scritub.com/stiinta/informatica/INTELIGENTA-ARTIFICIALA-Sintax41586.php" target="_blank" title="INTELIGENTA ARTIFICIALA - Sintaxa limbajelor de primul ordin - https://www.scritub.com">INTELIGENTA ARTIFICIALA - Sintaxa limbajelor de primul ordin</a>

eCoduri.com - coduri postale, contabile, CAEN sau bancare

Politica de confidentialitate | Termenii si conditii de utilizare

Copyright © Contact (SCRIGROUP Int. 2024 )