Imbogatirea structurilor de date

Îmbogatirea structurilor de date.

În acest capitol vom învata:

De ce este nevoie de îmbogatirea unei structuri

Cum arata un arbore pentru statistica de ordine

Care sunt pasii care trebuie parcursi pentru îmbogatirea unei structuri

Cum arata un arbore de intervale

In practica programarii apar câte o data situatii care necesita numai o structura de date clasica, ca de exemplu lista dublu înlantuita, tabela de dispersie sau arborele binar de cautare, însa majoritatea problemelor care trebuie rezolvate au nevoie de o structura noua. Totusi foarte far este nevoie sa se creeze un tip complet nou de structura de date. Mai des se potriveste sa fie suficient sa adaugam informatii suplimentare la o structura de date

clasica în asa fel încât ea saa raspunda nevoilor impuse de aplicatia pe care o realizam.

Desigur, îmbogatirea structurilor de date nu este întotdeauna simpla, deoarece informatia adaugata trebuie sa fie actualizata, si întretinuta prin operatiile obisnuite ale structurii de date respective.

Definim a i-a statistica de ordine a unei multimi de n elemente ca al i-lea cel mai mic element. De exemplu, minimul unei multimi de n elemente este prima statistica de ordine (i = 1), iar maximul este a n-a statistica de ordine (i = n). Intuitiv, o mediana este punctul de la jumatatea drumului. Când n este impar, mediana este unica, si apare pe pozitia i = (n+ 1)/2. Când n este par, exista doua median 414h78e e, care apar pe pozitiile i = n/2,

i = n/2+ 1.

Se poate arata ca orice statistica de ordine poate fi determinata într-un timp de O(n) în cazul unei multimi neordonate.

În acest capitol vom vedea cum se pot modifica arborii rosu-negri pentru ca orice statistica de ordine sa se determine într-un timp O(lg n) si vom afla cum se determina rangul unui element - pozitia acestuia în ordonarea liniara a multimii - tot într-un timp O(lg n).

In figura urmatoare vom prezenta o structura de date care poseda operatii rapide de statistici de ordine. Un arbore cu statistica de ordine T este un arbore rosu-negru care contine o informatie suplimentara în fiecare nod. La câmpurile uzuale pentru un nod x dintr-un arb ore rosu-negru: KEY(x), CUL(x), P(x), LS(x), si LD(x), se adauga un câmp nu DIM(x). Acest câmp contine numarul de noduri (interne) din subarborele cu radacina x (incluzându-l si pe x), adica dimensiunea subarborelui. Daca facem conventia DIM(NIL)=0, atunci are loc identitatea:

DIM(x)=DIM(LS(x))+DIM(LD(x))+1

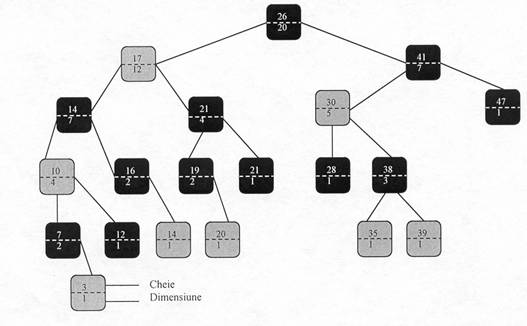
Un arbore de statistica de ordine care este de fapt un arbore rosu-negru îmbogatit. Nodurile gri sunt rosii, iar nodurile negre sunt negre. În partea de jos a fiecarui nod este câmpul DIM(x) care reprezinta numarul de noduri ale subarborelui cu radacina x.

Fig.12.1

Regasirea unui element cu rangul cunoscut.

Începem cu operatia care regaseste un element cu rangul cunoscut. Procedura RN-SELECT(x,i,y) retumeaza un pointer - y la nodul care contine a i-a cheie din subarborele având radacina x. Pentru a determina a i-a cea mai mica cheie din arborele de statistica de ordine T vom face apelul RN -SELECT( RAD(T),i,y).

RN-SELECT(X,i,y)

R=DIM(LS(x))+1

daca i=r atunci

y=x

altfel

daca i < r atunci

cheama RN-SELECT(LS(x))

altfel

cheama RN-SELECT(LD(x))

sdaca

sdaca

Return

Pentru a vedea cum functioneaza RN-SELECT, sa consideram cautarea pentru al 17 -lea cel mai mic element din arborele de statistica de ordine T din figura 12.1 . Se începe cu x egal cu radacina, a carei cheie este 26 ai cu i = 17.

Deoarece dimensiunea subarborelui stâng al lui 26 este 12, rangul radacinii va fi 13. Prin urmare, stim deja ca nodul cu rangul 17 este a117-13 = 4-lea cel mai mic element din subarborele drept al lui 26. Dupa apelul recursiv, x este nodul având cheia 41, iar i = 4.

Deoarece dimensiunea subarborelui stâng al lui 41 este 5, rangul sau în subarborele în care acesta este radacina, este 6. Prin urmare stim deja ca nodul cu rangul 4 este în al 4-lea cel mai mic element al subarborelui stâng al lui 41. Dupa apelul recursiv, x este nodul având cheia 30, iar rangul sau în subarborele pentru care el este radacina este 2. Asadar se face un nou apel recursiv pentru a-l determina pe al 14-2 =2-lea cel mai mic element din subarborele având radacina 38. La acest apel vom constata ca subarborele stâng are dimensiunea 1, ceea ce înseamna ca radacina 38 este al doilea cel mai mic element. În consecinta, acest ultim apel va întoarce pe y ca pointer la nodul având cheia 38 si executia procedurii se termina.

Deoarece fiecare apel recursiv coboara un nivel în arborele de statistica de ordine T, timpul total pentru acest algoritm este, în cel mai defavorabil caz, proportional cu înaltimea arborelui. Deoarece arborele este rosu-negru înaltimea sa este O(lg n), unde n este numarul de noduri. Prin urmare, timpul de executie al algoritmului prezentat este

O(lg n) pentru o multime dinamica avand n elemente.

Determinarea rangului unui element.

Fiind dat un pointer la un nod x dintr-un arbore de statistica de ordine T, procedura RN-RANG returneaza r = pozitia lui x în ordinea liniara data de parcurgerea în inordine a lui T.

RN-RANG(T,x,r)

R=DIM(LS(x))+1

y=x

cat timp y RAD(T)

daca y=LD(P(x)) atunci

r=r+DIM(LS(P(y)))+1

sdaca

y=P(y)

sciclu

return

Executia algoritmului RN-RANG pe arborele de statistica de ordine din figura 12.1 pentru determinarea rangului nodului având cheie 38 va produce urmatoarea secventa de valori pentru KEY(y) si r înregistrate la începutul corpului ciclului cat timp.

Iteratia KEY r

38 2

30 4

41 4

26 17

Procedura va returna rangul r = 17.

Fiecare iteratie a ciclului cat timp consuma un timp de O(1), iar y urca un nivel în arbore la fiecare iteratie, timpul de executie al algoritmului RN- RANG este, în cel mai rau caz, proportional cu înaltimea arborelui: O(lg n) pentru un arbore de statistica de ordine având n noduri.

Întretinerea dimensiunilor subarborilor.

Fiind data valoarea câmpului dimensiune din fiecare nod, procedurile RN-SELECT si RN-RANG pot calcula repede informtia de statistica de ordine. Nu am castigat nimic daca câmpurile nu se pot întretine eficient prin operatiile de baza ce modifica arborii rosu-negri. Vom arata acum ca dimensiunile subarborilor se pot întretine atât pentru inserare cât si pentru stergere, fara afectarea timpilor asimptotici de executie ai acestor operatii.

Inserarea unui nod într-un arbore rosu-negru se face în doua etape:

- se insereaza nodul x în arborele dat ca si cum ar fi un arbore binar de cautare obisnuit si se coloreaza inserat cu rosu

-se aplica asupra arborelui rezultat un algoritm care va recolora nodurile pentru conservarea proprietatilor specifice arborelui rosu-negru.

În prima faza se coboara în arbore începând de la radacina si se insereaza nodul nou ca fiu al unui nod existent. A doua faza înseamna urcarea în arbore, modificând culorile si efectuând la sfârsit rotatii pentru a conserva proprietatile rosu-negru.

Pentru a întretine dimensiunile subarborilor în prima faza, se va incrementa câmpul dimensiune[x] pentru fiecare nod x de pe drumul traversat de la radacina în jos spre frunze. Noul nod care se adauga va primi valoarea 1 pentru câmpul sau dimensiune. Deoarece pe drumul parcurs sunt O(lg n) noduri, costul suplimentar pentru întretinerea câmpurilor dimensiune va fi si el O(lg n ). În faza a doua, singurele modificari structurale ale arborelui rosu-negru sunt produse de rotatii, care sunt cel mult doua. Mai mult, rotatia este o operatie locala; ea invalideza numai câmpurile dimensiune din nodurile incidente (de la capetele) legaturii în jurul careia se efectueaza rotatia. La codul procedurii ROTEsTE-STANGA(T ,x) se adauga urmatoarele doua linii:

dimensiune(y)= dimensiune(x)

dimensiune(x)= dimensiune(LS(x))+ dimensiune(LD(x))+1

Figura de mai jos ilustreaza cum sunt actualizate câmpurile dimensiune. Pentru procedura ROTEsTE-DREAPTA modificarile sunt simetrice.

Deoarece la inserarea unui nod într-un arbore rosu-negru sunt necesare cel mult doua rotatii, se consuma un timp suplimentar de O(1) pentru actualizarea câmpurilor dimensiune, în faza a doua a inserarii. În concluzie, timpul total necesar pentru inserarea unui nod într-un arbore de statistica de ordine cu n noduri este de O(lg n) acelasi din punct de vedere asimptotic cu cel al arborilor rosu-negru obisnuiti.

stergerea unui nod dintr-un arbore rosu-negru are de asemenea doua faze: prima opereaza pe arborele binar de cautare, iar a doua face cel mult trei rotatii si în rest nu efectueaza alte modificari structurale ale arborelui. Prima faza elimina din arbore un nod y. Pentru a actualiza dimensiunile subarborelui, vom traversa un drum în sus de la nodul y la radacina si vom decrementa câmpurile dimensiune ale nodurilor de pe acest drum. Deoarece drumul are lungimea O(lg n), în cazul unui arbore rosu-negru cu n noduri, timpul suplimentar consumat cu întretinerea câmpurilor dimensiune în prima

faza a stergerii unui nod este de O(lg n). Cele O(1) rotatii din faza a doua a stergerii sunt gestionate în aceeasi maniera ca si în cazul inserarii. Prin urmare, atât inserarea cât si stergerea, inclusiv întretinerea câmpurilor dimensiune, consuma un timp O(lg n) pentru un arbore de statistica de ordine cu n noduri.

Cum se îmbogateste o structura de date.

La proiectarea algoritmilor apare frecvent problema îmbogatirii structurilor de date uzuale pentru ca acestea sa ofere functionalitate suplimentara.

Procesul de îmbogatire a unei structuri de date se poate împartii în patru pasi:

Alegerea unei structuri de date suport.

Determinarea informatiei suplimentare care trebuie inclusa si întretinuta în structura de date luata ca suport.

Verificarea posibilitatii întretinerii informatiei suplimentare în cazul operatiilor de baza care modifica structura suport.

Proiectarea noilor operatii.

Ca si în cazul altor metode de proiectare prezentate schematic, nu trebuie sa respectam exact pasii în ordinea de mai sus. Nu are nici un rost, de exemplu, sa se determine informatia suplimentara si proiectarea noilor operatii (pasii 2 si 4) daca nu se va putea întretine eficient informatia suplimentara memorata în structura de date. Totusi, aceasta metoda în patru pasi va asigura o abordare ordonata a eforturilor de îmbogatire a unei structuri de date si o schema de organizare a documentatiei referitoare la aceasta.

Pasii de mai sus au fast exemplificati la începutul capitolului pentru proiectarea arborilor de statistica de ordine. La pasul 1 am ales ca structura suport arborii rosu-negri. O indicatie asupra utilitatii acestor arbori la obtinerea statisticilor de ordine este data de eficienta operatiilor specifice multimilor dinamice pe o ordine totala, precum MINIM, MAXIM, SUCCESOR si PREDECESOR.

La pasul 2 am adaugat câmpurile dimensiune, care contin, pentru fiecare nod x, dimensiunea subarborelui având radacina x. În general, informatia suplimentara are ca scop sa faca operatiile (proprii structurii îmbogatite) mai eficiente. De exemplu, am fi putut implementa operatiile RN-SELECT si RN-RANG folosind numai cheile memorate în arbore, însa în acest caz timpul lor de executie nu ar mai fi fost O(lg n). Uneori aceasta informatie suplimentara contine referinte si nu date.

La pasul 3, ne-am asigurat ca operatiile de inserare si stergere pot întretine câmpurile dimensiune fara a-si altera eficienta asimptotica, ele executându-se tot într-un timp O(lg n). În cazul ideal, un numar mic de modificari ale structurii de date, trebuie sa fie suficient pentru a întretine informatia suplimentara. De exemplu, daca am memora în fiecare nod rangul sau din arbore, atunci operatiile RN-SELECT si RN-RANG s-ar

executa mai rapid, dar inserarea unui nou element minim în arbore, ar provoca modificarea acestei informatii (rangul) în fiecare dintre nodurile arborelui. În schimb daca memoram dimensiunea subarborilor în locul rangului, inserarea unui nou element va necesita modificari ale informatiilor doar in O(lg n) noduri.

La pasul 4, am proiectat operatiile RN-SELECT si RN-RANG. De fapt, îmbogatirea structurii de date este impusa tocmai de nevoia de a implementa noi operatii. Uneori informatia suplimentara se va putea folosi nu numai la proiectarea operatiilor noi, ci si la reproiectarea celor proprii structurii de date suport pentru a le îmbunatatii performantele.

Arbori de intervale.

Ne propunem sa îmbogatim arborii rosu-negri pentru a realiza operatii pe multimi dinamice de intervale. Un interval închis este o multime notata [t₁;t₂] =. În aceasta sectiune vom presupune ca intervalele cu care lucram sunt închise; extinderea rezultatelor la intervale deschise sau semideschise este imediata.

Intervalele reprezinta un instrument convenabil de reprezentare a evenimentelor care ocupa fiecare un interval continuu de timp. Am putea dori, de exemplu, sa interogam o baza de date de intervale de timp pentru a descoperi ce evenimente au aparut într-un anumit interval. Bazele de date temporale, de altfel, sunt la moda acum. Structura de date prezentata în aceasta sectiune ofera un mijloc eficient de întretinere a unei astfel de baze de date de intervale.

Intervalul [t₁;t₂] se poate reprezenta sub forma unui obiect i, care are

câmpurile jos[i] = t₁ (capatul inferior) si sus[i] = t₂ (capatul superior).

Spunem ca intervalele i si i' se suprapun daca i i' F adica daca jos[i] sus[i'] si

jos[i'] sus[i]. Pentru orice doua intervale i ~i i' are loc trihotomia intervalelor, adica ele verifica doar una din urmatoarele trei proprietati:

a. i si i' se suprapun,

b. sus[i] < jos[i'],

c. sus[i] < jos[i '].

În figura urmatoare sunt prezentate cele trei cazuri:

(a) 

(b) (c)

Numim arbore de intervale un arbore rosu-negru care întretine o multime dinamica de elemente, în care fiecare element x contine un interval int[x]. Arborii de intervale au urmatoarele operatii.

INSEREAZĂ(T, x) adauga la arborele de intervale T elementul x care are în câmpul int un interval.

sTERGE(T,x) sterge elementul x din arborele de intervale T.

CAUTA(T,x,r) retumeaza un pointer la un element din arborele de intervale pentru care int[y] se suprapune cu intervalul int[x], sau NIL daca în multime nu exista un astfel de element. 

În figura urmatoare vom ilustra modul de reprezentare al unei multimi de intervale cu ajutorul unui arbore de intervale. Vom aplica metoda în patru pasi descrisa mai înainte pentru a proiecta arborele de intervale si operatiile proprii acestuia.

(a)

(b)

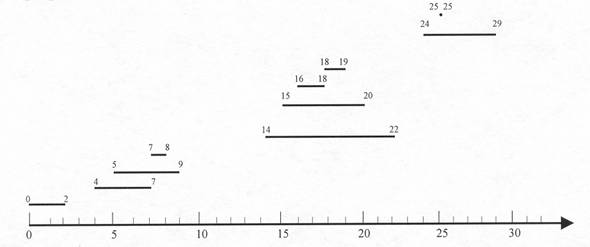
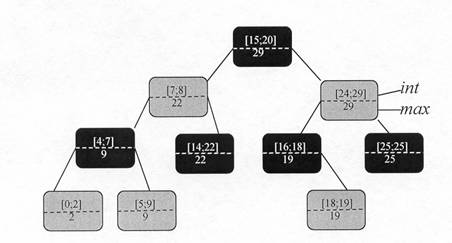
Figura (a) reprezinta 0 multime de 10 intervale, sortate de jos în sus dupa capatul din stânga (inferior), iar figura (b) reprezinta arborele de intervale corespunzator. Parcurgerea în inordine a acestui arbore va produce lista nodurilor sortata dupa capatul din stânga.

Pasul 1: Structura de date suport

Am ales ca structura suport un arbore rosu-negru în care fiecare nod x contine un câmp interval int[x] si pentru care cheia nodului x este capatul inferior, jos[int[x]], al intervalului. Prin urmare, o traversare în inordine a structurii de date va produce o lista a intervalelor, ordonata dupa capatul inferior al acestora.

Pasul 2: Informatia suplimentara.

Pe lânga câmpul int[x], fiecare nod x va contine o valoare max[x] care reprezinta valoarea maxima a capetelor intervalelor memorate în subarborele având radacina x. Deoarece capatul superior al fiecarui interval este cel putin la fel de mare ca si capatul inferior al acestuia, max[x] va fi de fapt valoarea maxima a capetelor superioare ale intervalelor memorate în subarborele având radacina x.

Pasul 3: Întretinerea informatiei suplimentare.

Inserarea si stergerea se pot executa într-un timp O(lg n) pe un arbore de intervale cu n noduri. Valoarea câmpului max[x] se determina usor daca se cunosc int[x] si valorile max ale fiilor nodului x cu :

max[x] = max(sus[int[x]], max[LS[x]], max[LD[x]]).

De fapt, actualizarea câmpurilor max dupa o rotatie se poate realiza într-un timp O(1).

Pasul 4: Proiectarea noilor operatii.

Singura operatie care trebuie proiectata este CAUTA(T ,i,x), care gaseste un interval din arborele T suprapus pe intervalul i. Daca T nu contine astfel de intervale se returneaza NIL altfel retumeaza x - pointer la intervalul cautat.

CAUTA(T,i,x)

x=rad[T]

Daca jos[i]>max[x] atunci x=NIL return

sdaca

cat timp x NIL si i nu se suprapune cu int[x]

daca LS[x] NIL si max[LS[x]] jos[i] atunci

x=LS[x]

altfel

x=LD[x]

sdaca

scattimp

Daca x≠NIL atunci i=x return

Altfel i=NIL

sdaca

Întrebari si exercitii la capitolul 12.

Exercitiul 1.

Verificati afirmatia: 'daca am memora în fiecare nod rangul sau din arbore, atunci operatiile RN-SELECT si RN-RANG s-ar executa mai rapid, dar inserarea unui nou element minim în arbore, ar provoca modificarea acestei informatii (rangul) în fiecare dintre nodurile arborelui' .

Exercitiul 2.

Scrieti algoritmul pentru INSEREAZA(T, x).

Exercitiul 3.

Scrieti algoritmul pentru sTERGE(T, x).

Exercitiul 4.

Scrieti algoritmul care gaseste toate intervalele i' pentru care sus[i] < jos[i '], unde i este un interval la intrare.

Exercitiul 5.

Care este complexitatea algoritmului de mai sus?