Limbajul LPA–Prolog
Obiective
Durata: 3 ore
Istoria programarii logice cuprinde cateva etape reprezentative:
1970 – Robert Kowalsky, Edinburgh University si Alain Colmerauer, Université d’Aix Marseille au pus bazele unei colaborari cu un obiectiv comun: utilizarea formalismului logicii matematice la definirea unui limbaj de programare. Cercetarile lui R. Kowalsky au constituit cadrul teoretic necesar, iar A. Colmerauer si P. Roussel au scris primul interpretor si au definit limbajul Prolog (PROgrammation LOGique). Primul compilator Prolog (Kowalsky) a fost realizat la Warren Edinburgh University, Department of AI.
1980 – Borland a elaborat versiunea Turbo Prolog, implementabila pe IBM PC, ceea c 121c23b e a dus la raspandirea si cunoasterea limbajului.
William Clocksin si Christopher Mellish publica in 1981 cartea „Programming in Prolog”, care defineste standardul Edinburgh al limbajului Prolog. Standardul Borland este mai restrictiv referitor la posibilitatile de calcul simbolic.
LPA (London Prolog Associates) elaboreaza LPA Prolog, care are la baza standardul Edinburgh, dar aduce si o serie de dezvoltari proprii (metapredicate).
Cele prezentate in cele ce urmeaza se refera la versiunea LPA Prolog, ce constituie totodata si suportul aplicatiilor prezentate. Implementarea LPA deriva din mai bine cunoscuta versiune Edinburgh Prolog, careia firma londoneza producatoare (London Prolog Associates) i-a adus imbunatatiri si dezvoltari suplimentare (metapredicate, facilitati grafice etc.). Versiunea de referinta Edinburgh Prolog a fost definita de W.F.Clocksin si C.S.Mellish in cartea “Programming in Prolog”, lucrare considerata la ora actuala un standard neoficial al limbajului Prolog.
Prolog este un limbaj declarativ, spre deosebire de alte limbaje (C, Pascal, Basic etc.) care sunt procedurale (descriu modul de rezolvare a problemelor).
2.1. Alfabetul si elemente de sintaxa limbajului Prolog
Alfabetul limbajului. La scrierea programelor Prolog se poate utiliza intreaga tabela de caractere ASCII, atat caracterele uzuale cuprinse in prima jumatate a tabelei (avand codurile ASCII cuprinse intre 0 si 127, fapt pentru care sunt denumite impropriu caractere pe 7 biti), precum si caracterele din cea de a doua jumatate a tabelei ASCII (avand codurile intre 128 si 256). Setul de caractere din partea superioara a tabelei ASCII depinde de pagina de cod sau fontul cu care se lucreaza. Acesta include de obicei literele grecesti, precum si diverse caractere semigrafice.
Separatori si terminatori. Principalul separator al termenilor limbajului este virgula (“, ”). Virgula poate sa apara de asemenea ca separator intre elementele unei liste (de fapt o lista este un caz particular de termen compus). Spatiul este utilizat ca separator intre termeni si operatori, de fiecare data cand natura acestora impune introducerea unui spatiu pentru delimitare (spatiul nu este necesar atunci cand termenii si operatorii sunt de natura diferita, adica unul este alfanumeric, iar celalalt simbolic). De exemplu, daca plus este un operator binar, iar ++ si ** sunt doi termeni, sintaxa termenului compus: ++plus** este corecta. Terminarea unui enunt Prolog se realizeaza prin caracterul punct (“.”) urmat in mod obligatoriu de spatiu sau terminatorul de sfarsit de linie (caracterele CR , LF). Punctul poate sa apara insa si in componenta unui termen simbolic cum ar fi **.**, context in care acesta nu are rol de terminator.
Comentariile. Pentru documentare, intr-un program Prolog se pot introduce oricand comentarii. In functie de intinderea (amploarea) acestora, exista doua modalitati de introducere a comentariilor. Caracterul % defineste drept comentariu continutul liniei, incepand cu caracterul insusi si pana la sfarsitul acesteia. Inserarea unui comentariu pe mai multe randuri se face incadrand textul respectiv intre delimitatorii /* si */.
2.2. Vocabularul si termenii limbajului Prolog
Termenii limbajului. In Prolog, termenii constituie tipurile fundamentale de date ale limbajului si pot fi utilizati atat pentru reprezentarea unor date elementare (scalare), cat si pentru reprezentarea unor structuri foarte complexe (de exemplu o baza de date relationala). Termenii sunt de fapt caramizile din care se compun clauzele limbajului (clauza este cel mai mic element sintactic avand semnificatie de sine statatoare in Prolog sau, mai exact, este cel mai mic enunt compilabil). Termenii pot fi simpli sau compusi.
Termenii simpli constituie practic vocabularul limbajului de programare, acestia fiind cele mai mici unitati lexicale avand o anumita semnificatie in cadrul limbajului. Termenii simpli sau atomici ai limbajului Prolog sunt numerele intregi sau reale, variabilele, atomii si sirurile de caractere. Un termen compus se formeaza prin combinarea unor termeni simpli si/sau compusi. Din categoria termenilor compusi fac parte listele si listele de octeti, termeni cu o aplicabilitate aparte in cadrul limbajului. In tabelul 1 este prezentata o clasificare a termenilor limbajului Prolog si sunt descrise predicatele predefinite prin care programatorul poate testa daca un termen apartine unuia din tipurile specificate mai sus. Totodata, predicatul type/2 permite determinarea tipului unui anumit termen dat.
Termeni simpli
Variabilele. O variabila este denumita in Prolog printr-un identificator care trebuie sa inceapa in mod obligatoriu cu o majuscula (o litera de la A la Z) sau cu caracterul “_” (“underscore”). Secventa de caractere din denumirea variabilei poate sa includa, de asemenea, caracterul “_”, acesta fiind de fapt considerat litera. De exemplu, urmatorii identificatori sunt denumiri corecte de variabile:
Anonim _variabila X Y Cristy
Numere intregi. Ca in oricare limbaj de programare, un numar intreg se reprezinta printr-o succesiune de cifre, eventual precedata de semnul plus sau minus. Conventia de reprezentare este algebrica pe 4 octeti, domeniul numerelor intregi reprezentabile fiind cuprins intre -2147483648 si 2147483647.
Numerele reale. Un numar real poate fi precedat de semn si este format dintr-o secventa de una sau mai multe cifre, punctul zecimal si o secventa de una sau mai multe zecimale. Optional numarul poate fi urmat (fara a se lasa spatiu) de litera e (sau E) si o secventa de cifre eventual precedata de semn (in format exponential). Dupa cum se poate constat, numerele reale au sintaxa similara cu cea din Pascal (punctul zecimal trebuie cadrat in mod obligatoriu de cifre). Fiecare din termenii de mai jos sunt corecti si reprezinta numere reale:
258.0752 -12.59432 2.0E7 +1.85e10 ,
in timp ce nici una din urmatoarele succesiuni de caractere
1. 12E3 12.3 E4
nu sunt corecte sintactic.
Numere intregi intr-o baza oarecare. Un numar intreg intr-o baza oarecare b se poate reprezenta in Prolog scriind baza b urmata de un apostrof si cifrele numarului in baza respectiva. De exemplu, succesiunea de caractere
2’1100100
este corecta si reprezinta reprezentarea in baza 2 a numarului 100. Acelasi numar se poate reprezenta in format hexazecimal (in baza 16) scriind 16’64. Pentru o mai buna edificare, la prompterul ?- al fereastra de dialog se pot introduce pe rand comenzile:
X is 16’64. <Enter> respectiv X is 2’01100100. <Enter>
si in ambele situatii interpretorul Prolog va raspunde prin X=100.
Trebuie evidentiat aici un caz similar si anume atunci cand in fata apostrofului apare cifra 0 (care evident nu poate fi baza unui sistem de numeratie), iar in locul cifrelor un caracter. In aceasta situatie secventa 0’<caracter> desemneaza codul ASCII al caracterului citat dupa apostrof. De exemplu termenul 0’d desemneaza numarul intreg 100, care este codul ASCII al caracterului “d”.
Atomii. Atomii sunt denumiri alfanumerice sau simbolice prin care programatorul poate desemna obiecte, proprietati ale acestora, precum si diverse relatii stabilite intre acestea. Lungimea maxima a unui atom este de 255 de caractere. Exista patru tipuri de atomi: alfanumerici, simbolici, de tip sir de caractere si atomi rezervati.
Atomi alfanumerici. Un atom alfanumeric este format dintr-o litera mica (a-z) urmata de o secventa formata din zero sau mai multe litere (a-z, A-Z) sau cifre (0-9). Caracterele din jumatatea superioara a tabelei ASCII sunt considerate litere mici. Utilizarea acestor caractere nu este insa recomanda din motivele deja mentionate la descrierea alfabetului. Urmatorii termeni sunt corecti si reprezinta atomi alfanumerici:
mar cristy michael bmw a123
Atomi simbolici. Un atom simbolic este format dintr-o secventa formata din unul sau mai multe din caracterele speciale enumerate mai jos:
$ & = - ^ ~ @
‘ ; - / + * ? < >
sau din caractere din partea superioara a tabelei ASCII. Urmatorii termeni
& && + ++ << >> -> <- */* <$>
constituie exemple corecte de atomi simbolici.
Atomi de tip sir. Un atom de tip sir sau “quoted” atom este o succesiune de caractere cuprinsa intre apostrofuri. Daca se doreste inserarea unui apostrof in cadrul sirului de caractere, atunci apostroful se dubleaza.
Caracterul ~ (tilda) poate fi utilizat pentru definirea unor caractere speciale sau de control. De exemplu termenul
‘~<Litera>’
semnifica caracterul <Ctrl> <Litera>, in timp ce termenul
‘~<Numar>’
reprezinta caracterul al carui cod ASCII este <Numar>, NumarI
Atomi rezervati. Atomii simbolici enumerati mai jos
! ; [] = :-
au o semnificatie prestabilita in cadrul limbajului si nu pot fi utilizati pentru denumirea unor entitati utilizator.
Sirurile de caractere. Un sir de caractere este o succesiune de caractere cuprinsa intre apostrofuri invers inclinate (caracterul `). Desi sirurile de caractere sunt considerate termeni simpli, deci de tip “atomic” (vezi tabelul 1), acestea nu sunt considerate atomi si nu trebuie confundate cu atomii “quoted”. Pentru a nu crea confuzii de acest tip, in cele ce urmeaza, pentru a desemna termenii de acest tip se va utiliza termenul strig. Deosebirea dintre un termen de tip “string” si un “quoted” atom consta in primul rand in modul intern de reprezentare al acestora. In plus, termenii de tip string pot fi supusi unor operatii proprii sirurilor de caractere. Exista totusi posibilitatea (predicatul atom_string/2) de a se realiza conversia de la atom la tipul string si reciproc.
Termenii compusi
Un termen compus are urmatoarea sintaxa:
functor(t1, t2, …, tn) ,
unde functor este un atom (de oricare din cele trei tipuri descrise mai sus), iar argumentele t1, t2, , …, tn sunt termeni, care pot fi simpli sau structurati la randul lor. Functorul defineste practic modul de structurare al termenului respectiv. Avand in vedere faptul ca numarul de argumente al functorului este variabil, iar gradul de imbricare este teoretic nelimitat, un termen compus poate reprezenta practic orice structura relationala de date, indiferent de gradul de complexitate al acesteia. In sintaxa imbricata a unui termen compus, functorul cel mai exterior este denumit functor principal.
Un termen compus are urmatoarea sintaxa:

Urmatoarele constructii sintactice reprezinta exemple corecte de termeni compusi: a(b, c(d, e(f, g))) alfa(X, Y) color(blue, yellow) +++(<<, >>, ok).
Functorul cel mai exterior se numeste functor principal.
Fiecarui termen ii este asociata o aritate (numarul de argumente). Termenii simpli au aritatea = 0, iar cei compusi au aritatea
Este a+b un termen Prolog? Da, +(a, b) este un termen Prolog de tip infix si aritate 2.
Structura descrisa de un termen compus poate fi ilustrata grafic prin reprezentarea acesteia sub forma unui arbore. Astfel, functorul principal va reprezenta si eticheta radacina arborelui, care va avea un numar de descendenti egal cu aritatea (numarul de argumente) functorului respectiv, fiecare dintre acestia corespunzand unuia din argumentele sale. Daca argumentul este un termen simplu, nodul corespunzator va constitui o frunza a arborelui, iar in caz contrar functorul respectiv va eticheta radacina unui subarbore construit in maniera recursiva astfel definita. De exemplu, primul dintre termenii citati mai sus se poate reprezenta printr-un arbore a carui multime de noduri este si a carui multime de muchii este , nodul a fiind radacina, iar b, d, f si g nodurile terminale sau frunzele arborelui respectiv.
Observatie. Un arbore este de fapt un graf neorientat, deci oricare dintre noduri poate fi considerat radacina arborelui. Totusi, avand in vedere situatia de fata nodul corespunzator functorului principal va fi considerat radacina arborelui.
Liste. O lista este o secventa formata dintr-un numar oarecare de elemente. O lista se poate reprezenta in Prolog enumerand, intre paranteze patrate, elementele sale componente separate prin virgula. De exemplu, urmatorii termeni sunt corecti si reprezinta liste:
[a, b, c, d] [jerry] [1, 2, 3, 4, 5] [a, 2, [1, 2, 3], a(b, c), d] []
Ultima dintre acestea constituie un caz particular si reprezinta lista vida (lista fara nici un element). Orice lista este compusa din cap si coada. Capul este primul element al listei, iar coada este lista formata din restul elementelor. De exemplu, prima din listele citate mai sus are capul a si coada [b, c, d], iar cea de a doua are capul jerry si coada []. Lista vida nu se poate descompune in cap si coada.
Listele sunt de fapt cazuri particulare de termeni compusi si au o aplicabilitate deosebita in limbajele de programare orientate spre calculul simbolic. Functorul care desemneaza o structura de tip lista este punctul, iar aritatea acestuia este 2. Primul argument este capul, iar cel de al doilea este coada listei. De exemplu, lista [a, b, c, d] se poate reprezenta, in sintaxa standard Edinburgh Prolog, prin termenul compus .(a, .(b, .(c, .(d, [])))). Atentie, nu se va lasa spatiu intre punct si paranteza deschisa. De fapt acest mod de scriere corespunde modului intern de reprezentare al listei, aceasta fiind de fapt un arbore binar. Data fiind insa lizibilitatea destul de redusa a acestei constructii sintactice, limbajul Prolog accepta reprezentarea sub forma de enumerare a listelor, dar aceasta reprezinta doar un mod de reprezentare externa a acestora. Tot pentru a veni in ajutorul programatorului o lista se poate exprima si sub forma:
[cap | coada]
deci despartind printr-o bara verticala capul listei de coada acesteia. Totodata o lista se poate descrie si sub forma:
[element1, element2, …elementn | coada],
dar avand grija ca dupa simbolul | trebuie scrisa o lista si nu un element. De exemplu, fiecare din termeni de mai jos este corect si reprezinta aceeasi lista [a, b, c, d]:
[a|[a, b, c, d]] [a, b|[c, d]] [a, b, c|[d]] [a, b, c, d|[]]
[a|[b|[c|[d]]]] [a, b|[c|[d]]] [a, b, c|[d|[]]]
Observatie. Modalitatile diverse de reprezentare a listelor permit, gratie mecanismului de unificare, extragerea si/sau identificarea elementelor componente ale unei liste.
Liste de octeti. O lista de octeti este o succesiune de caractere de orice tip cuprinsa intre ghilimele. Structura de date astfel definita consta in lista codurilor ASCII ale caracterelor care compun sirul. Pentru a insera caracterul “ in cadrul unei liste acesta se dubleaza. De exemplu termenul:
“Aceasta este o lista”
este corect si reprezinta lista
[65, 99, 101, 97, 115, 116, 97, 32, 101, 115, 116, 101, 32, 111, 32, 108, 105, 115, 116, 97].
Ca si in cazul atomilor de tip “quoted”, caracterul ~(tilda) poate fi utilizat pentru definirea unor caractere speciale, de exemplu termenul “~G” reprezinta lista [7].
Observatie. Listele de octeti nu trebuie confundate cu sirurile de caractere sau cu atomii de tip “quote”, dat fiind faptul ca acestea difera sintactic doar prin tipul de apostrofuri utilizate (“ ` respectiv ‘) pentru incadrarea succesiunii de caractere care le compun. Desi modul de reprezentare, structurile de date aferente si modul de operare cu aceste structuri sunt diferite, limbajul LPA Prolog dispune insa de predicate specifice care permit conversia intre oricare din cele trei tipuri (“quoted” atomi, siruri de caractere, liste de octeti).
Tabelul 1. Termenii limbajului Prolog
|
Tipul termenului |
predicat /aritate |
|||
|
termeni simpli simple |
variabila |
var /1, nonvar /1 |
||
|
atomic atomic |
atomi alfanumerici |
atom |
||
|
atomi simbolici |
atom |
|||
|
“quoted” atomi |
atom |
|||
|
numere number |
Intregi |
integer |
||
|
reale |
float |
|||
|
siruri de caractere |
string |
|||
|
termeni compusi |
termen compus functor(t1, t2, …, tn) (in particular liste, liste de octeti) |
compound |
||
2.3. Structura unui program PROLOG
Enunturile care intra in componenta unui program LPA Prolog pot fi de unul din urmatoarele tipuri:
clauze;
reguli de rescriere;
comenzi;
dintre care numai primele sunt obligatorii, ultimele doua tipuri de enunturi fiind optionale.
Regulile de rescriere permit programatorului definirea unui limbaj propriu prin definirea regulilor de rescriere prin care pot fi generate frazele limbajului respectiv. Cu alte cuvinte, aceste reguli nu sunt altceva decat productiile unei gramatici independente de context (concept definit de N. Chomsky), utilizata pentru generarea limbajului ce se doreste a fi definit. Odata ce un astfel de limbaj (gramatica) a fost definit (definita), programatorul poate testa daca un anumit enunt apartine sau nu limbajului respectiv. Aceste aspecte vor fi reluate si dezvoltate intr-unul din capitolele urmatoare.
O comanda este aproape identica cu o formula de interogare, singura deosebire constand in faptul ca aceasta are ca prefix simbolul :- (doua puncte liniuta). Prin urmare, formatul unei comenzi este:
:- predicat1, predicat2, …, predicatn . (k
Denumirea de comanda provine de la faptul ca termenii executabili din componenta acesteia sunt executati in mod automat la fiecare (re)incarcare a programului sursa care incorporeaza respectiva comanda De exemplu, daca intr-un program se insereaza comanda:
:- write(‘Hello !’), nl.
acesta ne va adresa un salut la fiecare incarcare a sa.
Clauzele limbajului
Clauzele sunt enunturile sau “caramizile” din care se compun programele Prolog. Altfel spus, clauza este cel mai mic enunt compilabil. Clauzele sunt de doua tipuri: fapte si reguli.
Un fapt este de forma:
antet.
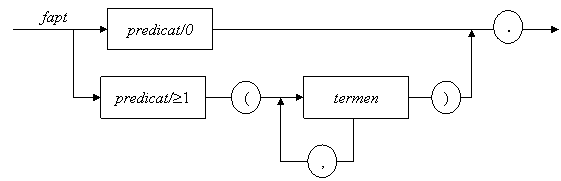
unde, din punct de vedere sintactic,
antet este un atom sau un termen compus,
al carui functor trebuie sa fie diferit simbolul „:-” sau „=”.
Sintactic, un fapt se termina prin punct, ce trebuie urmat obligatoriu de
spatiu sau de terminatorul de sfarsit de linie.
Un fapt are sintaxa unui termen si reprezinta un predicat, care poate fi de aritate 0 sau orice aritate
Intr-un limbaj Prolog, orice functor principal reprezinta un predicat. Argumentele oricarui predicat, daca exista, sunt termeni si nu pot fi alte predicate; de aceea, limbajul se numeste de ordinul I.
O regula este de forma:
antet :- t1, t2, …, tk. (1)
unde antet constituie capul sau concluzia regulii si apare in partea stanga a simbolului :-, iar t1, t2, …, tk, k 1 constituie premisele regulii. Fiecare tk este un predicat sau un termen executabil denumit in limba engleza “call term” sau “goal”. Regula este terminata printr-un punct urmat de spatiu sau terminatorul de sfarsit de linie. Intuitiv, un termen este denumit executabil daca consistenta sau valoarea de adevar a acestuia poate fi dedusa din contextul clauzelor programului Prolog. Din punct de vedere al logicii matematice, regula (1) este echivalenta cu implicatia (virgula are semnificatia de conjunctie logica, iar simbolul :- de implicatie inversa):
antet t1 t2 tk (2)
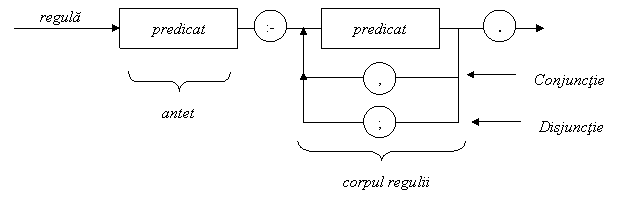 deci inferarea concluziei antet se poate face daca, pentru un
anumit mod de “instantiere” a variabilelor din componenta acestora,
premisele t1, t2, …, tk. pot
deci inferarea concluziei antet se poate face daca, pentru un
anumit mod de “instantiere” a variabilelor din componenta acestora,
premisele t1, t2, …, tk. pot
simultan satisfacute.
Pentru a intelege notiunea de termen executabil sau goal trebuie plecat de la premisa ca intr-un program Prolog orice functor principal este un simbol predicativ (predicat) si are in consecinta o valoare de adevar.
Daca in logica matematica scriem a b c, adica a b, scriem a c, in Prolog se obtine: a :- b; c. Multimea acestor clauze poarta denumirea de Program.
Definirea unui fapt de forma:
fapt(a1, …, ak).
presupune specificarea (asertarea) faptului ca predicatul fapt(a1, …, ak) este adevarat. Astfel faptele permit declararea unor piese de cunoastere presupuse adevarate (date, ipoteze), iar regulile specificarea unor reguli de inferenta (axiome, teoreme) prin care pot fi deduse noi fapte sau piese de cunoastere.
2.4. Aspectul declarativ si procedural al programelor Prolog
Caracteristica principala a limbajului Prolog consta in faptul ca este un limbaj declarativ, spre deosebire de cele procedurale (limbaje specializate in descrierea procedurala a rezolvarii unei probleme).
2.4.1. Aspectul declarativ
Operatia principala care se poate executa asupra termenilor limbajului Prolog este UNIFICAREA. Doi termeni S si T ai limbajului sunt unifiabili daca:
cei doi termeni sunt identici, SsT
substitutia sastfel incat sSssT
Exemplu: T = data(ziua, aprilie, A); S = data(Z, Luna, 2001);
s
sSssT = data(1, aprilie, 2001).
cmgu() = .
Regulile conform carora doi termeni doi termeni sunt unifiabili
daca S si T reprezinta doua constante, atunci acestea sunt unifiabile numai daca sunt identice;
daca unul din termeni este o variabila libera, atunci aceasta poate fi unificata cu orice termen (simplu sau compus);
daca ambii termeni sunt variabile libere, unificarea se realizeaza prin legarea celor doua variabile. Desi cele doua variabile nu sunt instantiate (initializate), ele se comporta ca si cum ar reprezenta o variabila unica; ca urmare, orice instantiere a uneia dintre variabile atrage dupa sine si instantierea celeilalte cu aceeasi valoare.
doi termeni compusi sunt unifiabili daca sunt indeplinite urmatoarele conditii:
au acelasi functor si aceeasi aritate;
argumentele de pe pozitiile corespunzatoare sunt unifiabile intre ele.
Un program Prolog este o secventa de clauze:
P :- Q, R.
P – consecinta logica a lui Q si R;
Pentru a demonstra P se demonstreaza mai intai Q, iar apoi se demonstreaza R. Programul Prolog poate fi interogat prin precizarea unei clauze obiectiv (goal):
(G): G , G2 Gn – pentru ce valori ale variabilelor, predicatele G1, G2 Gn sunt adevarate (simultan)? Sau, In ce conditii G este o consecinta logica a formulelor din program? Pentru ce valori ale variabilelor G este adevarata (satisfiabila)?
Definitia 1. Fie P = un program Prolog si Q o forma predicativa. Q este o consecinta logica a lui P sau Q este adevarata daca sunt indeplinite urmatoarele conditii:
o instanta I a unei clauze din P al carei antet este unifiabil cu Q: CIP si substitutia s astfel incat s Q = s antet(C);
Toate predicatele din corpul regulii C (daca exista) sunt adevarate (satisfiabile).
OBS. Un fapt poate fi privit ca o regula avant drept antet predicatul respectiv si al carei corp este clauza vida.
Daca formula Q contine variabile Q=Q(x1, x2, , xn), valorile variabilelor pentru care formula Q este adevarata sunt s(x1), s(x2), , s(xn).
2.4.2. Aspectul procedural
Fie P = un program Prolog si Q o forma predicativa. Q este o consecinta logica a lui P sau este satisfiabila din P daca:
s astfel incat sP sQ
Formula Q se numeste obiectiv (goal).

Interpretorul limbajului Prolog are
urmatorul mod de lucru:
Indicatorul yes inseamna ca exista o substitutie s astfel incat din P este deductibil Q (sP sQ), adica o instanta a lui Q este deductibila din P, deci Q este o consecinta logica a multimii P.
Indicatorul no inseamna ca din P nu este deductibil Q (sP sQ), adica Q nu este o consecinta logica a multimii P.
In cazul raspunsului yes¸ mecanismul inferential returneaza substitutia s
Variabilele instantiate (initializate) pot fi privite ca parametrii de intrare ai procedurii libere, iar variabilele libere ca parametri de iesire ai procedurii, parametri ce vor fi instantiati cu valorile corespunzatoare de interpretorul Prolog .
 Multimea clauzelor unui program care
corespund unui aceluiasi predicat poarta numele de procedura. Aceste proceduri sunt
mult mai flexibile decat cele din limbajele de programare. O procedura
Prolog poate fi aplicata in mai multe moduri (flow pattern), programatorul putand inversa parametrii de intrare
cu cei de iesire.
Multimea clauzelor unui program care
corespund unui aceluiasi predicat poarta numele de procedura. Aceste proceduri sunt
mult mai flexibile decat cele din limbajele de programare. O procedura
Prolog poate fi aplicata in mai multe moduri (flow pattern), programatorul putand inversa parametrii de intrare
cu cei de iesire.
Exemplu: Predicatul p/2 – i– input; o– output.
prieten(marius, ion).
:?– prieten(Cine, Cui). % (o, o)
:?– prieten (Cine, ion). % (o, i) Cine=maria
:?– prieten (maria, Cui). % (i, o) Cui=ion
:?– prieten (maria, ion). % (i, i) yes
Fiecare predicat executabil poate fi considerat ca o procedura, in sensul cunoscut din programarea clasica. O procedura mai returneaza si acel indicator de raspuns (yes sau no).
Dupa ce un program Prolog a fost editat si compilat, utilizatorul poate introduce in fereastra de dialog diverse formule de interogare a sistemului. O formula de interogare, denumita goal in terminologia engleza, este de forma:
p1, p2, … , pn. (n
unde p1, p2, …, pn sunt termeni executabili, iar virgula are semnificatia de conjunctie logica. O formula de interogare poate fi de doua feluri:
determinita nu contine variabile libere, raspunsul sistemului la o astfel de formula fiind yes sau no, dupa cum formula respectiva este sau nu o consecinta logica a clauzelor din program;
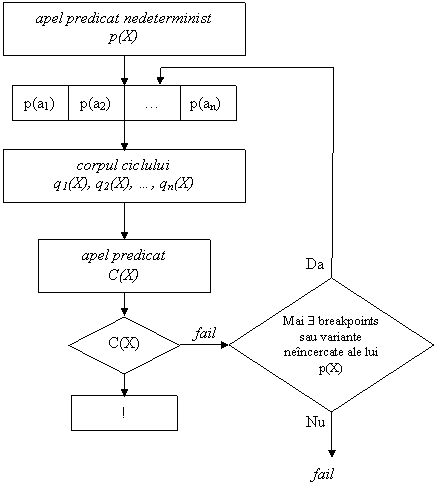
 nedeterminista: contine una sau mai multe variabile
libere, sistemul determinand prin backtracking
toate instantierile posibile ale
variabilelor pentru care respectiva formula este o consecinta
logica a clauzelor din program.
nedeterminista: contine una sau mai multe variabile
libere, sistemul determinand prin backtracking
toate instantierile posibile ale
variabilelor pentru care respectiva formula este o consecinta
logica a clauzelor din program.
Exemplu: place (ion, X) :- are_zestre(X), frumoasa (X).
are_zestre(X) :- bogata(Y), fata (X, Y).
:?– place (ion, Fata). %(i, o)
Remarca 1: De fiecare data cand are de satisfacut un goal introdus in fereastra de interogare sau din corpul unei reguli, interpretorul Prolog incepe scanarea tuturor clauzelor din program incepand cu prima dintre acestea, in vederea gasirii unei clauze al carei antet este unifiabil cu goal-ul curent.
cmgu .
Remarca 2: Daca un goal a fost unificat cu antetul unei reguli, se trece la demonstrarea predicatelor (subgoal-urilor) din corpul regulii respective. Incercarea de a satisface aceste fapte se face in ordinea in care acestea apar in corpul regulii. Astfel, se trece la a demonstra bogata (Y) – devine goal curent.
Remarca 3: Daca un predicat din corpul unei reguli a fost demonstrat, se trece la demonstrarea predicatului urmator; in caz contrar, se revine la ultimul punct de breakpoint aflat in program. Goal-ul curent devine fata(X, veta).
Cand mai multe clauze din program sunt unifiabile cu goal-ul curent, interpretorul plaseaza un punct de breakpoint pe urmatoarea clauza unifiabila din program.
fata(X, veta)
fata(geta, veta), sC
s s sC
frumoasa(geta).
Remarca 4: Cand un goal este dovedit inconsistent, se revine prin backtracking la ultimul punct de breakpoint plasat in program. O data cu revenirea la ultimul punct de breakpoint, se elibereaza toate variabilele instantiate dupa plasarea in program a respectivului punct de breakpoint. Variabila X este eliberata (dezlegata de valoarea geta).
Revenindu-se la punctul de breakpoint, variabila X este instantiata din nou cu valoarea maria. In acest caz, goal-ul frumoasa (maria) poate fi demonstrat si Prolog, tinand cont de substitutia curenta, raspunde Fata=maria.
Urmatoarele 2 caracteristici exprima o particularitate relevata a limbajului Prolog:
Singura modalitate de instantiere a unei variabile este procedura de unificare (programatorul nu poate atribui o valoare unei anumite variabile).
Variabilele pot fi eliberate numai prin mecanismul de backtracking al interpretorului Prolog.
In Prolog, simbolul „=” este un operator infix care face apel la procedura de unificare; in urma unificarii variabilelor din cei doi termeni, instantierea se realizeaza daca X este libera.
X=1+2 are drept efect instantierea lui X cu expresia 1+2 daca X este libera: s
X=1 are ca efect instantierea variabilei X = 1, daca X este libera. s
X=1, X=X+1: s 1=1+1 – inconsistent => fail, s, s (1)=s
 Exemple BAF si CAF:
Exemple BAF si CAF:
prezent(alina). prezent(georgiana). prezent(elena). prezent(mircea). prezent(dan).
lista:-
prezent(X), write(X), nl, fail.
lista. % BAF(Backtracking After Fail)
lista:-
prezent(X), write(X), nl, X=dan, !. % CAF(Backtracking After Fail)
Precizare: O formula de interogare Q trebuie privita ca un apel la mecanismul inferential al interpretorului (demonstratorul) Prolog, care genereaza solutiile lui Q.
2.5. Liste. Prelucrarea listelor
2.5.1. Listele Prolog
O lista este o colectie de zero sau mai multe obiecte. Lista fara nici un obiect se numeste vida si se reprezinta prin []. Celelalte liste sunt formate din:
cap, primul element;
coada, lista celorlalte elemente, in particular lista vida.
OBS: Lista vida [] nu se poate descompune in cap si coada.
In Prolog o lista se reprezinta printr-un termen compus. Orice termen poate fi reprezentat printr-un arbore. Fie termenul compus:
functor(termen 1, termen 2, , termen n).
radacina arborelui este etichetata cu functorul principal al termenului (functor).
fiecarui nod etichetat cu un termen compus (radacina) ii corespunde un numar de descendenti egal cu aritatea termenului respectiv. Acesti descendenti vor fi etichetati cu argumentele termenului respectiv.
nodurile care corespund unor termeni simpli (atomici) sunt noduri finale.
Listele fac exceptie de la aceasta regula, fiind reprezentate prin functorul „.” de aritate 2 (cap si coada).
Exemplu: [1, 2, a, b, evrika, 29]
(1, . (2, . (a, . (b, . (evrika, . (29))))))
Sa se descrie arborele asociat listei de mai sus!
Exemplu de lista: [1, 2, a, b | [evrika | [29]]]. Termenul amplasat dupa simbolul | trebuie sa fie o lista.
2.6. Operatori
Dat fiind faptul ca limbajul Prolog este orientat mai degraba in vederea efectuarii calculelor simbolice decat numerice, operatorii trebuie priviti ca un mod aparte de reprezentare a termenilor compusi de aritate unu sau doi. Deci un operator nu semnifica de regula efectuarea unei operatii, ci indica mai degraba modul de agregare a operanzilor in cadrul structurii desemnata de acel operator. Exista totusi si o serie de operatori prin care programatorul poate forta la nevoie evaluarea unei expresii. Spre deosebire de sintaxa standard a unui termen compus, situatie in care functorul precede paranteza ce contine lista argumentelor sale, operatorii permit scrierea termenilor de aritate 1 sau 2 intr-o noua sintaxa, care intr-un anumit context poate fi mult mai agreabila.
Operatii cu termeni. Orice operator care constituie functorul principal al unui termen compus are o semnificatie predicativa si are in consecinta o valoare de adevar. In functie de rolul si semnificatia acestora, operatorii utilizabili la formarea “expresiilor” Prolog se pot imparti in urmatoarele patru categorii precizate mai jos.
Operatorul de unificare Cea mai importanta operatie pe multimea termenilor este unificarea (de fapt aceasta este operatia de baza a limbajului Prolog). Se stie ca doi termeni t1 si t2 se numesc unifiabili daca exista o substitutie s astfel incat termenii s(t1) si s(t sa devina identici. Operatia de unificare este desemnata prin operatorul infix =. Termenul executabil t1=t2 este de fapt un apel la rutina de unificare a interpretorului Prolog. Daca cei doi termeni sunt unifiabili, atunci predicatul t1=t2 este satisfacut si variabilele libere din cei doi termeni sunt substituite prin valorile lor corespunzatoare din cmgu(t1, t2). In caz contrar, termenul t1=t2 este inconsistent, iar variabilele din componenta acestora raman nemodificate.
Se poate testa daca doi termeni t1=t2 sunt unifiabili si fara a produce instantieri ale variabilelor prin apelarea predicatului predefinit unifiable(t1, t2).
Operatorul = este complementul operatorului =. Astfel t1=t2 este adevarat daca t1 si t2 sunt neunifiabili si este fals cand t1 si t2 sunt unifiabili.
Operatori de comparatie lexicografica Operatorul == (doua semne de egalitate) permite compararea lexicografica a doi termeni. Termenul (predicatul) t1==t2 este valid daca cei doi termeni t1 si t2 sunt lexicografic identici. De exemplu, termenul a+b==b+a este inconsistent, deoarece termenii a+b si b+a nu sunt identici, in schimb predicatul a+b==a+b este valid. Operatorul == (back slash si doua semne de egalitate) este negatia operatorului precedent. Astfel, predicatul a+b==b+a este adevarat, in timp ce predicatul a+b==a+b este fals. Operatorii din aceasta categorie nu produc instantieri ale variabilelor.
Operatorul de evaluare Dupa cum s-a precizat mai sus, limbajul Prolog este orientat pentru efectuarea calculului simbolic, operatorii fiind utilizati mai degraba pentru reprezentarea unor structuri. Evident, sfera de utilizare a limbajului ar fi puternic diminuata, daca acesta nu ar permitea efectuarea unor calcule matematice. Dar, aceste calcule se fac numai la cererea expresa a programatorului. De exemplu, daca X este o variabila libera, termenul executabil X = 1+2 are ca efect instantierea variabilei X cu valoarea (termenul) 1+2 (ceea ce era de asteptat intrucat 1+2 este substitutia de unificare a celor doi termeni ai operatorului =). Operatorul prin care programatorul poate cere in mod expres evaluarea unei expresii este desemnat prin atomul rezervat is. In partea stanga a operatorului is trebuie sa apara in mod obligatoriu o variabila (libera sau nu), iar in partea dreapta o expresie algebrica, ale carei variabile (daca exista) sa fie initializate cu valori numerice. Astfel, daca X este o variabila libera, apelul termenului X=1+2 va avea ca efect instantierea variabilei X cu valoarea 3. Trebuie mentionat faptul ca un termen executabil de forma:
X is <Expresie>
nu trebuie confundata cu o instructiune de atribuire. De fapt, desi pare oarecum socant, limbajul Prolog nu are instructiune de atribuire !. Mai mult, un predicat de forma:
X is X+1 ,
este inconsistent, deoarece variabila X din membrul drept trebuie sa fie instantiata si, indiferent de valoarea acesteia, aceasta nu poate fi nici cum egala cu X+1.
Dupa cum s-a mentionat anterior, in Prolog unificarea este singurul mod de instantiere a unei variabile, dupa cum mecanismul de backtracking este singurul mod posibil de eliberare al acesteia.
Operatori relationali Limbajul Prolog contine urmatorii operatorii relationali, ce pot fi utilizati pentru comparatia numerica a doua expresii. Toate variabilele cuprinse in cele doua expresii trebuie sa fie instantiate in momentul apelului termenului respectiv.
E1=:=E2 egalitate
E1==E2 neegalitate
E1<E2 mai mic
E1=<E2 mai mic sau egal
E1>E2 mai mare
E1>=E2 mai mare sau egal
Fiecare din termenii de mai sus produce evaluarea numerica a expresiilor algebrice E1 si E2, valoarea de adevar a termenilor de mai sus fiind calculata ca in orice alt limbaj de programare. Operatorii relationali nu produc instantieri ale variabilelor din cele doua expresii.
Observatie. Operatorii mai mic sau egal si mai mare sau egal trebuie scrisi in maniera ilustrata mai sus, scrierile <= respectiv => nefiind acceptate de compilatorul Prolog.
2.7. Controlul backtraking-ului in limbajul Prolog
Exista doua procedee prin care programatorul poate interveni in functionarea procedurii de backtraking:
predicatul fail (predicat inconsistent), are drept efect fortarea mecanismului de breaktraking pentru revenirea in ultimul breakpoint plasat in program;
predicatul cut (predicatul !) este consistent (valid) si are drept efect suprimarea punctelor de breakpoint plasate de predicatele precedente acestuia din corpul regulii in care acesta se gaseste sau a breakpoints corespunzatoare unor clauze ale predicatului ce constituie antetul regulii.
 Exemple:
Exemple:
1) % max/3
a) max(A, B, A):- A>=B.
max(A, B, B):- B>A.
b) max(A, B, A):- A>=B, !.
max(A, B, B):- B>A.
c) max(A, B, A):- A>=B, !.
max(A, B, B).
2) a:-b, c, !, d, e.
a:-f, g.
h:-k, l, a, m.
3) Membru al unei liste
member(X, L), X – element, L – lista.
: determinist (i, i) sau nedeterminist (o, i).
Implementarea se face tinand cont ca un element apartine unei liste daca:
o este un element al capului listei;
o face parte din coada listei respective.
member(X, [X|_]).
member(X, [_|T]):- member(X, T).
:?– member(b, [a, b, c]). %(i, i) yes
:?– member(X, [a, b, c]). %(o, i) X=a; X=b ; X=c.
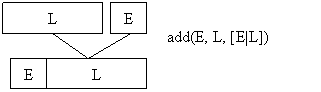
4) Adaugarea unui element la
lista data
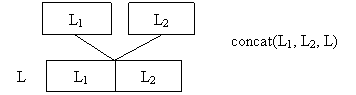
5) Concatenarea a doua liste
concat([], L, L).
concat([H|T], L2, [H|T2]):- concat(T, L2, T2).
6) Stergerea uni element al unei liste
del(X, L, L1).
Prin stergerea unui element X din lista L se obtine lista L1.
del(X, [X|T], T).
del(X, [H|T], [H|T1]):- del(X, T, T1).
:?– del(b, [a, b, c, b, d], L).
L=[a, c, b, d]
L=[a, b, c, d]
7) Inserarea unui element intr-o lista
insert(X, L, L1):- del(X, L1, L).
8) Permutarea elementelor unei liste perm (L, L1)
perm([], []).
perm([H|T], L):- perm(T, T1), insert(H, T1, L).
9) Numararea elementelor unei liste count(L, N)
count([], 0).
count([H|T], N):- count(T, M), N is M+1.
sau
count([], N, N).
count([_|T], Numar, N):-
NouNumar is Numar+1, count(T, NouNUmar, N).
Numar se va initializa cu zero.
:?– count([1, 2, 3, 4, 5], 0, Cate).
Cate=5
count(L, N):-count(L, 0, N).
:?– count([1, 2, 3, 4, 5], Cate). Cate=5.
 REZUMAT
REZUMAT
Limbajul LPA Prolog reprezinta un instrument simplu si eficient de abordare a problemelor specifice de Inteligenta artificiala. Aceste caracteristici sunt conferite de urmatoarele aspecte principale ale limbajul Prolog:
Sintaxa simpla.
Un program Prolog reprezinta, in general, o colectie de clauze (fapte si reguli) care descriu problema (prin reprezentarea cunostintelor), fara a fi necesara descrierea algoritmului de rezolvare!
Orice clauza are o valoare de adevar (fals sau adevarat), purtand si denumirea de predicat.
Nu exista instructiunea de atribuire! O variabila primeste valori numai prin instantiere, generata de mecanismul de UNIFICARE.
Variabilele pot fi eliberate de valori numai prin mecanismul de BACKTRACKING al interpretorului Prolog. Prin backtracking se revine la punctele de intrerupere din program si astfel noi substitutii sunt automat testate.
 PROBLEME PROPUSE
PROBLEME PROPUSE
Pornind de la intriga si personajele din binecunoscutul film Santa Barbara, sa se scrie un program Prolog care sa corespunda etapelor precizate mai jos.
Sa se descrie urmatoarele fapte prin clauze Prolog
|
predicat: femeie(persoana) |
predicat: barbat(persoana) |
|
Pamela este femeie. Sophia este femeie. Minx este femeie. Augusta este femeie. Julia este femeie. Santana este femeie. Kelly este femeie. Eden este femeie. Laken este femeie. Rosa este femeie. |
CC este barbat. Mason este barbat. Lionel este barbat. Cruz este barbat. Ted este barbat. Brick este barbat. Brandon este barbat. Warren este barbat. |
|
predicat: mama(mama, fiica/fiu) |
predicat: tata(tata, fiica/fiu) |
|
Sophia este mama lui Eden. Sophia este mama lui Ted. Sophia este mama lui Brick. Sophia este mama lui Kelly. Augusta este mama lui Warren. Augusta este mama lui Laken. Minx este mama lui Lionel. Rosa este mama lui Santana. Santana este mama lui Brandon. |
CC este tatal lui Mason. CC este tatal lui Eden. CC este tatal lui Ted. Lionel este tatal lui Brick. Lionel este tatal lui Laken. Lionel este tatal lui Warren. |
Descrieti urmatoarele reguli prin clauze Prolog
|
Predicat |
Antet |
Descrierea (corpul) regulii |
|
parinte(parinte, copil) |
parinte(X, Y) |
if X este mama lui Y sau if X este tatal lui Y. |
|
tata(tata) |
tata(X) |
if X este tatal cuiva („ _”) |
|
mama(mama) |
mama(X) |
if X este mama cuiva. |
|
parinte(parinte) |
parinte(X) |
if X este parintele cuiva. |
|
bunica(bunica, nepot) |
bunica(X, Y) |
if X mam lui Z si Z este parintele lui Y. |
|
bunic(bunic, nepot) |
bunic(X, Y) |
if X este tatal lui Z si Z este parintele lui Y. |
|
sora(persoana, persoana) |
sister(X, Y) |
if X este femeie, M este mama lui X si M este mama lui Y, X<>Y, T este tatal lui X si T este tatal lui Y. |
|
frate(persoana, persoana) |
frate(X, Y) |
if X este barbat, M este mama lui X si M este mama lui Y, X<>Y, T este tatal lui X si T este tatal lui Y. |
Lansati programul in executie (Comanda Run Compile) si chestionati rezolver-ul Prolog:
|
Natural language question |
Prolog goal |
|
Este Kelly femeie? |
?:- femeie(kelly). |
|
Este Eden barbat? | |
|
Cine este femeie? | |
|
Cine este mama lui Eden? | |
|
Cine este tatal lui Kelly? | |
|
Este CC tatal lui Mason? | |
|
Al cui tata este CC? | |
|
A cui mama este Sophia? | |
|
Al cui frate este Mason? | |
|
Cine este bunica lui Brandon? | |
|
Este Brandon tatal lui Kelly? | |
|
Cine este bunic? | |
|
Este CC tatal lui Brandon? |
Problema 2: Podurile din Königsberg
Grafurile constituie un instrument practic si eficient de reprezentare a obiectelor si a relatiilor dintre acestea. Teoria grafurilor a fost introdusa la inceputul secolului al XVIII-lea de matematicianul austriac Leonhard Euler in vederea solutionarii celebrei probleme cunoscuta sub numele de “podurile din Königsberg”. Königsberg este un orasel austriac asezat pe ambele maluri ale raului Pregel, rau care formeaza doua insule. Malurile si cele doua insule sunt conectate prin sistemul de poduri ilustrat in figura 1a. Problema, care a framantat multe persoane pana la Euler, este urmatoarea: poate un calator sa parcurga intregul orasel, trecand pe fiecare pod, fara sa parcurga un pod de doua ori ?
 Multi au incercat sa
gaseasca o solutie, insa fara succes. Euler este
acela care a demonstrat matematic ca problema nu are solutie!,
imaginand grafurile pentru reprezentarea problemei (fig. 1b). Problema de
mai sus, cunoscuta sub numele de “lant eulerian” intr-un graf,
nu mai pune azi nici un fel de probleme, cunoscandu-se faptul ca un
astfel de drum exista daca numarul nodurilor de conectivitate
impara este 0 sau 2. Problema este cunoscuta si sub
denumirea de “lant (drum) hamiltonian”, Hamilton aducandu-si
contributia la stabilirea unor algoritmi pentru generarea acestor drumuri.
Mai mult, se stie ca intr-un graf exista un circuit eulerian
daca si numai daca graful este conex si pseudosimetric. Un
graf este pseudosimetric daca din fiecare varf pleaca atatea arce
cate intra in varful respectiv.
Multi au incercat sa
gaseasca o solutie, insa fara succes. Euler este
acela care a demonstrat matematic ca problema nu are solutie!,
imaginand grafurile pentru reprezentarea problemei (fig. 1b). Problema de
mai sus, cunoscuta sub numele de “lant eulerian” intr-un graf,
nu mai pune azi nici un fel de probleme, cunoscandu-se faptul ca un
astfel de drum exista daca numarul nodurilor de conectivitate
impara este 0 sau 2. Problema este cunoscuta si sub
denumirea de “lant (drum) hamiltonian”, Hamilton aducandu-si
contributia la stabilirea unor algoritmi pentru generarea acestor drumuri.
Mai mult, se stie ca intr-un graf exista un circuit eulerian
daca si numai daca graful este conex si pseudosimetric. Un
graf este pseudosimetric daca din fiecare varf pleaca atatea arce
cate intra in varful respectiv.
Revenind la problema podurilor din Königsberg, baza de cunostinte se poate reprezenta utilizand un predicat denumit “leaga” si utilizand doua astfel de predicate pentru fiecare pod:
leaga(i1, i2, p1). leaga(i2, i1, p1).
leaga(m1, i1, p2). leaga(i1, m1, p2). leaga(m1, i1, p3). leaga(i1, m1, p3).
leaga(m1, i2, p4). leaga(i2, m1, p4). leaga(m2, i1, p5). leaga(i1, m2, p5).
leaga(m2, i1, p6). leaga(i1, m2, p6). leaga(m2, i2, p7). leaga(i2, m2, p7).
unde, s-a notat prin: i1, i2 - cele doua insule; m1, m2 - cele doua maluri ale raului; p1, p2, p3, p4, p5, p6, p7 - cele sapte poduri.
Considerand dif(p, q) predicatul care exprima faptul p si q reprezinta doua poduri diferite, in limbajul de calcul al predicatelor, existenta unui drum eulerian s-ar putea reprezenta prin expresia urmatoare:
X1( X2( X3( X4( X5( X6( X7(
leaga(X1, X2, P1) leaga(X2, X3, P2) leaga(X3, X4, P3) leaga(X4, X5, P4) leaga(X5, X6, P5) leaga(X6, X7, P6) leaga(X7, X8, P7) dif(P1, P2) dif(P1, P3) dif(P1, P4) dif(P1, P5) dif(P1, P6) dif(P1, P7) dif(P2, P3) dif(P2, P4) dif(P2, P5) dif(P2, P6) dif(P2, P7) dif(P3, P4) dif(P3, P5) dif(P3, P6) dif(P3, P7) dif(P4, P5) dif(P4, P6) dif(P4, P7) dif(P5, P6) dif(P5, P7) dif(P6, P7)
exista_lant_eulerian
Domeniul variabilelor: X1..X7I .
Fara a avea pretentia ca este cea mai simpla forma de solutionare a problemei, daca un astfel de drum exista, predicatul: exista_lant_eulerian va avea valoarea true.
 TEST DE AUTOEVALUARE
TEST DE AUTOEVALUARE
Care este principalul separator al termenilor limbajului:
a. «!» (semnul exclamarii).
b. «, » (virgula) .
c. «;» (punct si virgula).
Terminarea unui enunt Prolog se realizeaza prin caracterul:
a. Punct («.») .
b. Spatiu.
c. Punct si virgula.
Inserarea unui comentariu pe mai multe randuri se face incadrand textul respectiv intre:
a. Paranteze ().
b. Delimitatori /* si */ .
c. Ghilimele (
O variabila incepe obligatoriu cu o majuscula sau cu caracterul:
a.
b.
c.
Un „quated” atom se defineste ca fiind:
a. succesiune de caractere cuprinsa intre apostrofuri.
b. succesiune de cifre cuprinse intre paranteze.
c. succesiune de termeni separati prin virgula unul de celalalt.
Care din urmatoarele forme defineste sintaxa unui termen compus:
a. x y = y x.
b. functor(t1, t2, …, tn) .
c. functor(!).
Clauza de tip fapt este de forma:
a. fapt(V1, V2, …, Vn).
b. antet.
c. antet t1 t2.
Clauza de tip regula are forma:
a. antet:-t1, t2, …, tk .
b. functor(t1, t2, …, tk).
c. /* regula */.
Predicatul = se numeste:
a. instantiere.
b. unificare.
c. backtracking.
Functorul unei liste este caracterul:
a. Virgula.
b. Dolar.
c. Punct.
Predicatul ‚fail’ este un predicat:
a. Consistent.
b. Inconsistent.
c. Valid.
Predicatul ‚cut’ are ca efect suprimarea punctelor de:
a. Breaktracking.
b. Breakpoint.
c. Breaktrace.
Caracterul % are rolul de:
a. Comentariu pana la sfarsit de linie.
b. Calcul in procente.
c. Salt la sfarsitul clauzei.
Constructia [a, b, c, d] reprezinta:
a. Un set de date.
b. O lista.
c. O multime.
Predicatul conditional IF este descris sintactic prin secventa:
a.
b. «:-:»
c.
1. b 6. b 11. b
2. a 7. b 12. b
3. b 8. a 13. a
4. c 9. b 14. b
5. a 10. c 15. c
v v v
|