Structuri si strategii de cautare in spatiul de stari
Obiective
Durata:
2 ore
4.1. Inteligenta artificiala ca reprezentare si cautare
In lucrarea “ACM Turing Award Lecture”, Newell si Simon (1976) demonstreaza ca activitatea inteligenta, umana sau artificiala, se realizata prin intermediul:
Simbolurilor pentru reprezentarea aspectelor semnificative din domeniul problemei;
Operatii pe aceste simboluri pentru generarea unor potentiale solutii ale problemei;
Cautarea in vederea selectarii unei solutii dintre aceste posibilitati.
Cu alte cuvinte, trebuie definita o reprezentare simbolica a obiectelor din domeniul aplicatiei si trebuie definiti niste operatori prin care se poate modifica aceasta reprezentare.
Rezolvarea unei probleme de catre o “masina ganditoare” presupune reprezentarea cunostintelor si cautarea solutiei, cele doua principii fiind intr-o interdependenta reciproca.
4.1.1. Reprezentarea cunostintelor
Inainte ca un calculator sa poata incepe solutionarea unei probleme, trebuie ca detaliile problemei respective sa fie reprezentate si codificate intr-un limbaj inteles de calculator. Programatorul de inteligenta artificiala trebuie sa abstractizeze aceste detalii si sa introduca in calculator numai acele date indispensabile rezolvarii problemei.
4.1.2 Cautarea
Un al doilea aspect subliniat de Newell si Simon este acela ca o problema este solutionata prin cautarea solutiei printre niste alternative posibile. Acest aspect este sus& 414i89e #355;inut de analogia cu gandirea umana. Omul utilizeaza de asemenea un numar de strategii in modul lui de a rezolva o problema. De exemplu, un jucator de sah analizeaza un anumit numar de miscari viitoare, alegand miscarea in functie de un criteriu de eficienta, astfel ales incat sa-i asigure un avantaj maxim. Un matematician alege dintre diferite strategii, nu mai putin complexe, pe acelea care-i permit demonstrarea unei teoreme complexe; un fizician poate investiga un anumit numar de cauze posibile ale unui anumit fenomen s.a.m.d. Acest aspect al inteligentei contureaza asa numita tehnica de rezolvare prin cautare in spatiul de stari.
Prin stare se intelege o anumita configuratie a problemei investigate. De exemplu, in jocul de sah o stare este o anumita pozitie de pe tabla de sah. In calculator, o pozitie este reprezentata printr-o asa numita baza de date, baza a carei complexitate depinde de natura problemei abordate, mergand de la cateva numere pana la o baza de date relationala. In procesul de rezolvare a unei probleme, omul sau masina poate utiliza anumite reguli, poate aplica anumite procedee sau artificii sau, in cazul jocurilor, poate efectua anumite mutari. De exemplu, in jocul de sah poate efectua oricare din mutarile posibile. Aceste reguli, procedee sau mutari vor produce modificari asupra bazei de date, aceasta reflectand starea curenta a problemei.
Totalitatea acestor stari vor constitui un spatiu pe care-l vom denumi spatiul de stari. Dintre acestea, vom deosebi o stare denumita stare initiala reflectand datele initiale ale problemei. De asemenea, starile ce constituie solutii posibile ale problemei vor fi denumite stari finale.
Grafurile constituie un instrument practic si eficient de reprezentare a obiectelor si a relatiilor dintre acestea. Teoria grafurilor a fost introdusa la inceputul secolului al XVIII-lea de matematicianul austriac Leonhard Euler in vederea solutionarii celebrei probleme cunoscuta sub numele de “podurile din Königsberg”.
Grafurile ofera un instrument ideal de reprezentare al spatiului de stari al unei probleme. Astfel, nodurile vor reprezenta starile distincte ale problemei, iar arcele regulile, operatiile sau mutarile efectuate in procesul de rezolvare al problemei. La un astfel de graf deosebim un nod corespunzator starii initiale, nod ce va constitui radacina grafului. De asemenea, graful va contine cel putin un nod care va constitui starea finala sau solutia problemei (evident, in ipoteza ca problema are solutie). Acest astfel de nod este denumit nod final sau goal.
Utilizand grafurile pentru reprezentarea spatiului de stari, rezolvarea problemei se reduce la cautarea in graful asociat a unui drum de la nodul initial la unul din nodurile finale.
O implementare eficienta a unui algoritm de cautare cere programatorului sa analizeze si sa prevada comportarea algoritmului, acesta fiind confruntat cu urmatoarele probleme:
conduce algoritmul respectiv la o solutie?
algoritmul conduce la o solutie intr-un numar finit (rezonabil) de pasi sau poate intra intr-un ciclu infinit?
daca o solutie este gasita este aceasta optima?
cat de amplu este procesul de cautare in termenii timpului de calcul consumat si al memoriei afectate?
Exemplul 1. Este foarte cunoscut asa numitul joc 15-Puzzle constituit din 15 jetoane patrate numerotate de la 1 la 15 dispuse intr-un chenar, jucat de majoritatea copiilor. Fie, pentru simplitatea reprezentarii, un joc 8-puzzle:
Cateva aspecte interesante privitoare la procesul de rezolvare a problemelor pot fi evidentiate pe acest joc.
Desi miscarile fizice sunt efectuate prin mutarea micilor jetoane numerotate de la 1 la 8, este mult mai simplu sa ne imaginam ca mutam spatiul liber reprezentat prin patratelul negru. Astfel, urmatoarele mutari sunt permise:
mutarea patratelului negru in sus
mutarea patratelului negru la dreapta
mutarea patratelului negru in jos
mutarea patratelului negru la stanga
Pentru a aplica aceste mutari, trebuie avut grija ca patratelul negru sa nu paraseasca tabla de joc. Prin urmare, nu toate dintre cele patru mutari sunt aplicabile la un moment dat. De exemplu, cand patratelul negru este intr-unul din colturi numai doua din miscari sunt posibile.
Daca se specifica o stare initiala si una finala, se poate reprezenta graful de cautare propriu problemei propuse. Starile se pot reprezenta ca tablouri 3 3. Utilizand calculul predicatelor, o stare, sau baza de date curenta se poate reprezenta printr-un predicat “stare” continand 9 argumente. De exemplu, starea initiala poate fi reprezentata utilizand predicatul:
stare(1,4,3,7,0,6,5,8,2)
unde s-a notat cu 0 patratelul negru.
Patru proceduri, definind cele patru miscari posibile vor defini arcele grafului de reprezentare a spatiului de stari. Ca si in cazul precedent, multe stari pot avea diferiti descendenti, prin urmare digraful asociat nu este o arborescenta. Un drum de la starea initiala la starea finala in digraful astfel generat nu reprezinta altceva decat strategia sau secventa de miscari care conduce la rezolvarea problemei.
Trebuie de remarcat ca in acest caz digraful generat nu mai este aciclic, o anumita configuratie a dispunerii celor 8 numere putandu-se repeta in cadrul jocului. Dar, daca in graful generat exista un drum de la starea initiala la cea de goal atunci exista sigur si un drum elementar intre cele doua stari. Explorand numai drumurile elementare riscul ca algoritmul de cautare sa “pice” intr-un ciclu infinit este exclus.
7 8 8 6 6 4 8 up left down right left right up down left right up down Fig.
1. Spatiul de stari in cazul unui
8-puzzle
4.2. Strategii de cautare
Clasificarea algoritmilor de cautare
1. Directia de cautare
cautare directa („forward chaining”, „data driven”): se porneste de la starea initiala si se identifica drumul catre starea finala.
cautare inversa („forward chaining”): se porneste de la goal si ajunge in starea initiala.
cautare mixta: cautare in ambele directii.
2. Spatiul de cautare
cautare completa (exhaustiva), pe intreaga multime S.
cautare incompleta, pe o multime S ’ S. Este cercetat numai un subspatiu al multimii S („hill climbing”, „beam search”).
3. Strategia de cautare
irevocabila (fara revenire, metode de gradient).
cu revenire sau backtracking.
4. Exploatarea informatiei stocate in starea curenta (informativitate)
cautare oarba sau neordonata „blind search”).
cautare euristica (informata), estimeaza distanta de la starea curenta la solutie in vederea selectarii celui mai promitator descendent.
4.2.1. Algoritmi de cautare exhaustiva
Cautarea pe intreg spatiul de stari poate fi implementata cu ajutorul a doi algoritmi reprezentativi:
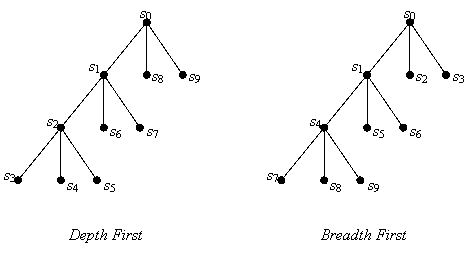
Depth First (cautare in adancime);
Breadth First (cautare pe nivel).
In implementarea celor doua metode de cautare se utilizeaza doua liste:
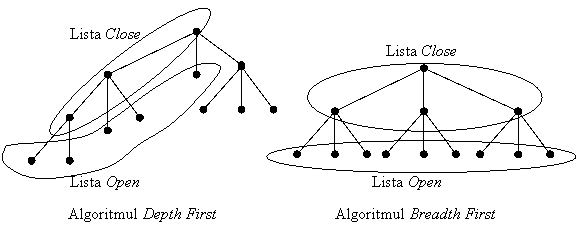
Lista Open contine starile care urmeaza a fi expandate (explodate, cercetate);
Lista Close contine starile care au fost deja cercetate.
Elementele acestor liste sunt de forma (s, p): s – stare curenta, p –starea parinte.
s s s s s s s s s s Breadth First s s s s s s s s s s Depth First
4.2.1.1. Algoritmul Depth-First (cautare in adancime)
procedure DepthFirst
begin
Open [(s0¸ nil
Close
while Open [ ] do
begin
extract ((s, p), Open)
insert ((s, p), Close)
if goal (s) then begin
compune_solutia; exit/continue;
end;
D
for d in D do
if ((d, Open) ((d, Close) then insert ((d,s), Open);
{Se insereaza (d,s) la inceputul listei Open);
end;
writeln(‘Problema nu are solutie
end
Lista Close Lista Open Algoritmul Depth First Algoritmul Breadth First Lista Close Lista Open
Dezavantajele
cautarii de tip Depth First:
nu gaseste in general solutia optima;
algoritmul se poate pierde in explorarea unor ramuri foarte lungi, programul putand fi intrerupt datorita depasirii resurselor de memorie.
Exemplu: Sa se descrie evolutia listelor Open si Close in problema de cautare reprezentata mai jos prin algoritmul Depth First.
Rezolvare
Open [ a], Close
Open x = a
D(x) =b, e, i;
Close [ a], Open b, e, i
2. x = b, Open = e, i
Dx=c, d;
Close [ a, b], Open c, d, e, i
3. x = c, Open = d, e, i Close [ a, b, c],
4. x = d, Open = e, i Close [ a, b, c, d],
5. x = e, Open = i Close [ a, b, c, d, e],
D(x)= d, f; % d nu se mai examineaza
Open f, i
6. x = f, Open = i Close [a, b, c, d, e, f],
D(x) = g, h; Open = g, h, i
7. x = g, Open =[h, i Close [ a, b, c, d, e, f, g].
In lista Close se regasesc perechile (S, P) – (Stare, Parinte)
(b, a), (c, b), (d, b), (e, a), (i, a), (f, e), (g, f).
Solutia problemei: a e f g
D(x) – multimea descendentilor starii x
4.2.1.2. Algoritmul Breadth-First (cautare pe nivel)
Daca algoritmul Depth First implementeaza o strategie de tip stiva (LIFO), algoritmul Breadth First are la baza o strategie de tip coada (FIFO).
s s d d d Close Open
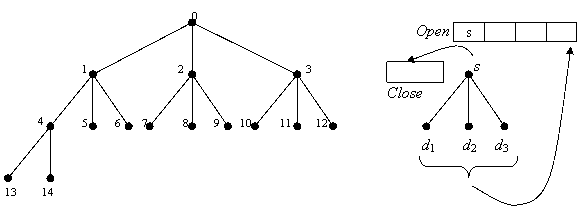Algoritmul Breadth-First
este simular cu cel prezentat la
metoda Depth First, cu diferenta ca starea (d,s)
se insereaza la sfarsitul listei Open
si nu la inceputul acesteia (v. fig. de mai jos).
Avantaj: gaseste solutia de lungime minima.
Dezavantaj: resursele de memorie necesare sunt foarte mari, acestea crescand exponential cu nivelul de adancime explorat.
2.2. Algoritmi de cautare euristica
George Polya asocia termenul „euristic” semnificatia de studiu al metodelor si regulilor descoperirii si inventicii. In dictionarul limbii romane contemporane euristic = adjectiv al procedeelor metodologice cu semnificatia care serveste la descoperirea unor solutii noi.
Lenat (1982): prin euristica se defineste acel tip de cunoastere avand caracterul de rationament bazat pe experienta, specializare, generalizare si analogie cu ajutorul caruia se efectueaza o interpretare, se ia o decizie sau se actioneaza in vederea atingerii unui obiectiv.
Euristic = euristico = a descoperi <<EUREKA>>
In IA, cautarea euristica se utilizeaza in 2 sisteme de baza:
Problema nu are solutie exacta datorita inerentelor ambiguitati din datele problemei. Un diagnostic medical poate fi un exemplu in acest sens: aceleasi simptome pot avea la baza mai multe cauze. Un medic utilizeaza o euristica pentru stabilirea celui mai probabil diagnostic.
Problema are o solutie exacta, dar resursele necesare determinarii acesteia pot fi inaccesibile sau insurmontabile. Ex: jocul de sah are 10120 stari.
Fie S – spatiul starilor si f : S A (N ) denumita euristica care face o evaluare a starilor avand sIS, f(s) desemnand sansa sau probabilitatea ca s sa se gaseasca pe drumul cel mai scurt spre solutia problemei.
Functia f se mai numeste si functie cost sau lungime. O stare este cu atat mai buna cu cat f este mai mic. Se calculeaza min f(di) pentru 1 i k, adica se alege descendentul de la care costul determinarii solutiei este cel mai mic. Se spune ca descendentul dmin are sanse mai mari sau se gaseste cu o probabilitate mai mare pe drumul optim de la starea s la solutia problemei.
Atunci cand spatiul starilor este foarte mare, acesta nu poate fi memorat sau parcurs intr‑un timp rezonabil.
Cautarea euristica este incompleta, dar informationala. Avand in vedere caracterul incomplet al cautarii, un algoritm de cautare euristica poate conduce la o solutie suboptimala sau poate chiar esua, in sensul ca nu poate determina o solutie. Cu toate acestea, in multe situatii cautarea euristica constituie singurul mod de rezolvare a unei mod a unei probleme.
Cautarea euristica poate fi:
completa sau incompleta. Cele incomplete pot fi cu 1 descendent (Hill Climbing) sau cu cativa (cei mai buni – Beam search);
cu revenire sau fara revenire (Hill Climbing).
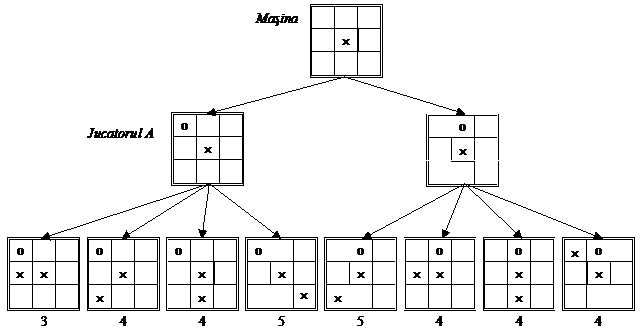
Exemplul 1: TIC–TAC–TOE
Se considera ca masina (calculatorul) joaca prima (cu simbolul ×), iar jucatorul cu caracterul o. Euristica se defineste astfel: unei stari oarecare i se atribuie ca valoare euristica numarul posibilelor combinatii (linii+coloane+diagonale) castigatoare ale calculatorului, deci numarul liniilor/coloanelor/diagonalelor care contin × si nu contin simbolul o.
Exemplul 2: 8 puzzle
h (s) – numarul jetoanelor care nu se gasesc pe pozitia corecta.
Starea
s
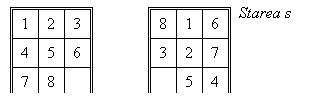h (s) – suma deplasarilor jetoanelor
spre pozitia corecta.
h (s) = 8.
h (s) = 1+1+3+3+1+1+3+3= 16.
Algoritmul „Hill climbing”
A fost propus si aplicat de Pearl in 1984. Este un algoritm fara revenire si cu o strategie incompleta. Este aplicabil in probleme de optimizare utilizand metoda gradientului.
Se urmareste optimizarea functiei f(x1, x2,, xn), in sensul determinarii max f, si fie vectorul solutie Xk la pasul k ,
Solutia la pasul k+1 se stabileste astfel:
In acest mod, mergand pe gradient, se asigura traseul catre valoarea de max (local sau global) a functiei f.
Cautare oarba: cataratorul este nerabdator si orb. Se alege panta cea mai abrupta pana cand se ajunge la un punct de la care nu se mai poate continua: s-a atins solutia sau s-a ajuns la un maxim local. Cautarea poate sa esueze. Samuel Pearl a utilizat cu succes acest algoritm in implementarea jocului de dame.
Algoritmul „Beam search”
Este un algoritm cu revenire (backtracking), cu cautare incompleta. Din multimea succesorilor se retin numai aceia cu sanse maxime (si relativ apropiate) de a figura pe drumul optim.
Algoritmul BEST FIRST (cu revenire)
s s d d d Close Ordonare
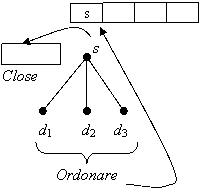Acest algoritm se obtine din algoritmul Depth First cu amendamentul ca
descendentii starii curente sunt ordonati crescator, prin
functia de evaluare, inainte ca acestia sa fie depusi la
inceputul listei Open.
Euristica f este conceputa in modul urmator:
f(s) = g(s) + h(s),
g(s) – adancimea starii s;
h(s) – estimare euristica a lungimii (costului) solutiei pornind de la starea s.
procedure BestFirstSearch
begin
Open [(s¸ nil, 0, h(s)]; Close
while Open [ ] do
begin
extract ((s, p, g, h), Open)
insert ((s, p, g, h), Close)
if goal (s) then begin
compune_solutia (Close); exit;
end;
D:={dI S | 
for d in D do
begin
gc := g + Cost(t); fc := gc + h(d);
end;
case d of
(d, _, _, _) Open Close: insert ((d, s, gc, fc), Open);
(d, pe, ge, fe)IOpen
if fc<fe then
begin
remove ((d, pe, ge, fe), Open);
insert ((d, pc, gc, fc), Open);
end;
(d, pe, ge, fe)IClose
if fc<fe then
begin
remove ((d, pe, ge, fe), Close);
insert ((d, pc, gc, fc), Open);
end;
end; {case}
Ordoneaza(Open); { f minimal pe prima pozitie
end; {while}
writeln(‘Problema nu are solutie
end;
Operatori s g a b c d e f i j k l h m p r i j k l m n p r q g g h f s a b c d e f h n q
Exemplul 1: Cautare intr-un spatiu cu
obstacole
Euristica: f(s) = f(x, y) = |xg–x| + |yg–y|. f(s) = 5.
Exemplul 2: 8 puzzle
h(s)
– numarul pieselor care nu se gasesc in pozitia corecta
(fara a include spatiul liber);
Functia de evaluare va fi de forma f(s) = g(s) + h(s):
g(s) – adancimea sau costul cu care a fost generata starea s;
h(s) – estimare euristica a costului solutiei pornind din starea s.
Starea
curenta Starea
finala (goal) g h = 3 f = 4 h = 5 f = 6 h = 5 f = 6 g h = 3 f = 5 h = 4 f = 6 h = 3 f = 5 g h = 2 f = 5 h = 4 f = 7
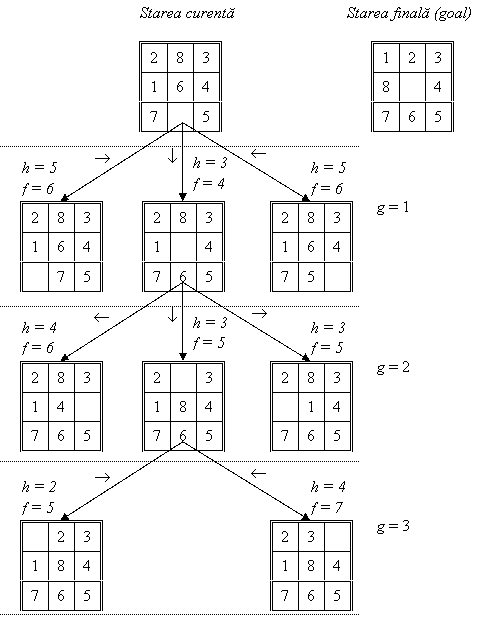
Rezolvarea unei probleme de catre o “masina ganditoare” presupune reprezentarea cunostintelor si cautarea solutiei.
Tehnica de rezolvare prin cautare in spatiul de stari presupune reprezentarea simbolica a obiectelor din domeniul aplicatiei (definirea parametrilor de stare) si definirea unor operatori prin care se poate modifica aceasta reprezentare (functii generatoare de stari).
Spatiul de stari asociat unei probleme este frecvent reprezentat sub forma arborescenta.
Cautarea solutiei se poate realiza prin mai multe tehnici (algoritmi): exhaustiva (in adancime, pe nivel), cu evaluare euristica (de ex., Best First), cu sau fara revenire.
Problema 1: Utilizand metodele a) Depth First; b) algoritmul Breadth First si c) Best First, sa se gaseasca drumul de la Start la Goal in labirintul din figura de mai jos.
Start Goal
Ordinea operatorilor:
Problema 2: Sa se descrie evolutia listelor Open si Close in problema de cautare reprezentata mai jos, prin algoritmul Breadth First.
TEST DE AUTOEVALUARE
Prin stare intelegem:
a. Un instrument practic si eficient de reprezentare a obiectelor.
b. O anumita configuratie a problemei investigate.
c. Reprezentarea cunostintelor si cautarea solutiei.
Spatiul de stari reprezinta:
a. Totalitatea regulilor, procedeelor sau mutarilor care produc modificari asupra bazei de date.
b. Totalitatea grafurilor.
c. Totalitatea starilor din domeniul problemei.
Estimarea distantei de la starea curenta la solutie, in vederea selectarii celui mai promitator descendent, se realizeaza prin:
a. Cautare completa.
b. Cautare euristica.
c. Cautare neordonata.
Depth First reprezinta un algoritm de:
a. Cautare pe nivel.
b. Cautare fara revenire.
c. Cautare in adancime.
La implementarea algoritmilor Depth First si Breadth First, lista Close contine:
a. Starile care au fost cercetate.
b. Starile initiale si finale.
c. Totalitatea starilor posibile.
Algoritmul Beam Search prezinta:
a. Cautari euristice incomplete cu un descendent.
b. Cautari euristice incomplete cu cativa descendenti.
c. Cautari euristice complete.
Lista Open contine:
a. Starile care au fost cercetate.
b. Starile ce urmeaza a fi cercetate.
c. Starile ce nu vor fi cercetate.
Best First reprezinta un algoritm cu evaluare euristica a descendentilor de tip:
a. Cautare in adancime.
b. Cautare pe nivel.
c. Cautare fara revenire.
Breadth First reprezinta un algoritm de:
a. Cautare in adancime.
b. Cautare pe nivel.
c. Cautare cu revenire sau backtracking.
Algoritmul Hill Climbing realizeaza:
a. Cautari euristice incomplete cu un descendent .
b. Cautari euristice complete.
c. Cautari euristice incomplete cu cativa descendenti.
Raspuns
1. b 3. b 5. a 7. b 9. b
2. c 4. c 6. b 8. a 10. a.
|
