Notiunea de graf neorientat, adiacenta, incidenta, grad

Notiunea de graf neorientat, adiacenta, incidenta, grad.

Definitie: Se numeste graf neorientat, o pereche ordonata de multimi (X,U), unde:

-    & 515b13f nbsp;   & 515b13f nbsp; X este o multime finita si nevida de elemente numite vârfuri sau noduri;

-    & 515b13f nbsp;   & 515b13f nbsp; U este o multime de perechi neordonate de câte doua elemente de X, numite muchii sau arce.

Asadar un graf neorientat poate fi reprezentat sub forma unei figuri geometrice alcatuita din puncte (vârfuri, noduri) si linii drepte sau curbe care unesc aceste puncte (muchii, arce). Respectând o anumita "traditie" pe care o gasim în literatura de specialitate, vom folosi:

-    & 515b13f nbsp;   & 515b13f nbsp; pentru grafuri neorientate termenii de "vârf" si "muchie";

-    & 515b13f nbsp;   & 515b13f nbsp; pentru grafuri orientate termenii de "nod" si "arc".

Daca o muchie trece prin nodurile x si y, atunci ea se noteaza [x,y] sau (x,y).

Exemplu:

Pentru graful G=(X,U) din figura 1, avem:

v     X= multimea vârfurilor (nodurilor);

v     U= multimea muchiilor (arcelor);

v     Muchiile sunt: u₁=(1,2), u₂=(2,3), u₃=(3,4), u₄=(2,4), u₅=(5,6)

Pe caz general, într-un graf neorientat G=(X,U), notam:

·    & 515b13f nbsp;   & 515b13f nbsp;  m numarul muchiilor, n numarul vârfurilor;

·    & 515b13f nbsp;   & 515b13f nbsp;  X= multimea vârfurilor, U= multimea muchiilor;

·    & 515b13f nbsp;   & 515b13f nbsp;  o muchie u_k este o pereche neordonata (a,b) alcatuita din doua elemente din X.

Pentru o muchie u_k=(a,b), vom spune ca:

Ř    & 515b13f nbsp;   vârfurile a si b sunt adiacente si se numesc extremitatile muchiei u_k;

Ř    & 515b13f nbsp;   muchia u_k si vârful a sunt incidente în graf. La fel, muchia u_k si vârful b;

Ř    & 515b13f nbsp;   muchia (a,b) este totuna cu (b,a) (nu exista o orientare a muchiei).

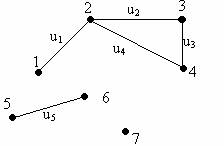Figura 1.

Definitie: Gradul unui vârf x, notat d(x), reprezinta numarul muchiilor care trec prin nodul x (incidente cu nodul x).

Exemplu:

În graful din figura 1, d(2)=3 (prin nodul 2 trec trei muchii, si anume muchiile u₁, u₂, u₃).

·    & 515b13f nbsp;   Un vârf care are gradul 0, se numeste vârf izolat (de exemplu, vârful 7 în graful din figura 1).

·    & 515b13f nbsp;   Un vârf care are gradul 1 se numeste vârf terminal (de exemplu, vârfurile 5 si 6 în graful din figura 1).

Teorema

Într-un graf G=(X,U) cu n vârfuri si m muchii, suma gradelor tuturor vârfurilor este egala cu 2*numarul muchiilor.

Demonstratia este evidenta. Fiecare muchie de forma [x_i, x_j] (unde x_i si x_j sunt vârfuri,  cu i, j ), contribuie cu o unitate la gradul vârfului i si cu o unitate la gradul vârfului j. Asadar fiecare muchie adauga doua unitati la suma gradelor. Fiind m muchii, rezulta foarte clar ca suma gradelor este 2*m.