Notiunile de graf partial si subgraf
Definitie: Fie G=(X,U). Un graf partial al lui G, este un graf G1=(X,V), cu V U. Altfel spus, un graf partial G1 este chiar G, sau se obtine din G pastrând toate vârfurile si suprimând niste muchii.
Exemplu:
Pentru graful G=(X,U) de mai jos, construim alaturat graful partial obtinut prin eliminarea muchiilor ce trec prin vârful 4. Acesta este G1=(X,V), unde X= , iar V= (s-au eliminat muchiile u3 si u4 care trec prin nodul 4).
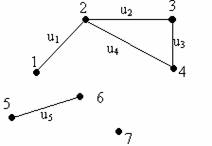
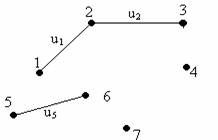
Figura 3a. Figura 3b.
Definitie: Fie graful G=(X,U). Un subgraf al lui G, este un graf G1=(Y,T), unde Y X si T U, iar V va contine numai muchiile care au ambele extremitati în Y. Altfel spus, un subgraf G1 se obtine din G eliminând niste vârfuri si pastrând doar acele muchii care au ambele extremitati în multimea vârfurilor ramase.
Exemplu:
Pentru graful G=(X,U) din figura 3.a, construim subgraful obtinut prin eliminarea vârfurilor 1 si 6 (figura 4). Acesta este G1=(Y,T), unde Y= , iar T= (s-au eliminat nodurile 1 si 6, precum si muchiile u1 si u5 care trec prin aceste noduri).
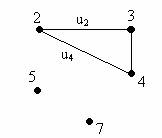
Figura 4.
|