PROIECT la disciplina Algoritmi si Structuri de date
-Cuprins-
I. TEORIE..3
Sistem informational-sistem informatic.3
Notiunile cu care opereaza algoritmii
Grafuri neorientate
Arbori
Tablouri unidimensionale
II. PROBLEME.19
In schema logica si program
o Probleme de logica
o Alte probleme
Problema de complexitate crescuta
In program
o Probleme de logica
TEORIE
Sistem informational-Sistem informatic
Un sistem informatic poate fi privit ca un ansamblu de elemente interconectate si interconditionate prin relatii fizice, sociale si de alta natura, intre elesi cu mediul extern sistemului, care functioneaza in vederea realizarii unui scop sau a finalizarii unui obiect.
Procesele desfasurate intr-o activitate organizata nu au loc la intamplare,ci sunt declansate de anumite informatii, care prelucrate , servesc la luarea unor decizii.Aceste decizii determina executarea unor serii de operatii.
Deci activitatea desfasurata intr-un sistem organizat,in vederea realizarii unui obiectiv poate fi definite ca fiind rezultatul actiunii conjugate, a trei subsisteme ce actioneaza intr-o stransa interdependenta si care la randul lor pot fi considerate sisteme:
-sistemul de conducere sau decisional(S.D.)
-sistemul condos, de executie sau operational(S.O.)
-sistemul informational.
Sistemul de conducere are
rolul de a dispune,
Sistemul condus are rolul de a executa pracric deciziile luate si de a furniza date privind actiunile realizate sau in curs de executie, folosind pentru aceasta resursele materiale, financiare stiitifice si uman existente, repartizate pe obiective dinainte stabilite.
Pentru axecutarea activitatilor de baza
ale procesului decisional:planificare,
Sistemul informational este un
instrument
Sistemul informational cuprinde fondul de informatii,tehnicile de colectare si stocare, mijloacele si metodele necesare in vederea prelucrarii si transmiterii informatiilor.
Deci sistemul informational este un ansamblu de fluxuri si circuite informationale organizate intr-o conceptie unitara. Ele utilizeaza modele,proceduri ,resurse umane si materiale pentru colectarea ,inregistrarea, prelucrarea, stocarea si/sau transmiterea datelor si a informatiilor, prin intermnediul carora asigura interconexiunile informationale dintre sistemul de conducere si sistemul condus, dintre elementele componente ale acestor sisteme, dintre organismul social economic pe care il serveste si mediul social economic extern. Scopul final al sistemului informational (SI) este realizarea obiectivelor proprii organismului social-economic in concordanta cu obiectivele generala ale societatii si in conditii de maxima eficienta.
Sistemul informational primeste intrari, le prrlucreaza si furnizeaza iesiri.Intrarile si iesirile unui system informational sunt date, informatii si decizii.
Ansamblul operatiilor la care sunt supuse intrarile pentru a furniza iesirile se constitue in proceduri.
In functie de mijloacele si procedeele
utilizate pentru executarea operatiilor, acestea pot fi grupate in proceduri
manuale, proceduri automate, proceduri mecanizate sau mixte. In cazul cand
metodele, procedurile si mijloacele utilizate pentru pentru colectarea,
inregistrarea, prelucrarea, stocarea si/sau transmiterea datelor si a informatiilor
sunt cu preponderenta automatizate, sistemul informational devine un sistem
informatic.De remarcat faptul ca cele doua notiuni, cea de sistem informational
sic ea de sistem informatic nu sunt in mod substantial diferite, din punc de
vedere a scopurilor
Singura diferenta se reduce la gradul de automatizare a proceselo de prelucrare a datelor si informatiilor.
Sistemul informatic reprezinta un ansamblu de elemente intercorelate functional in scopul automatuzarii obtinerii informatiilor necesare conducerii in procesul de elaborare a deciziilor.
Notiunile cu care opereaza algoritmii
Algoritmii opereaza cu urmatoarele notiuni:
Un algoritm prelucreaza datele de intrare in scopul obtinerii unor rezultate (a datelor de iesire) utilizand si date intermediare.
Datele sunt valori concrete specifice fiecarei probleme care vor fi retinute de calculator in anumite zone de memorie.
Dimensiunea zonelor de memorie depinde de tipul datelor respective.
Intuitiv, memoria poate fi reprezentata ca locatii succesive (zone de memorie) identificate prin adrese (numere de ordine).
Programatorul are sarcina de a gandi algoritmul unei probleme si de a utiliza cat mai eficient memoria.
In program datele apar fie sub forma unor constante (valori cunoscute anticipat, care nu se modifica pe parcursul executiei), fie sub forma de variabile. Constantele si variabilele sunt obiectele informationale de baza manipulate intr-un program.
Putem defini o variabila ca fiind un nume dat unei zone de memorie.
Datele se caracterizeaza printr-un anumit tip care va determina :
-o anumita multime din care data poate lua valori
- un anumit mod de reprezentare in memoria calculatorului
- o multime de operatori care pot fi aplicati acestor valori.
- tipul unei date determina lungimea zonei de memorie ocupata de acea data. In general, lungimea zonei de memorare este dependenta de calculatorul pe care s-a implementat compilatorul.
Datele se pot clasifica dupa tipul lor in:
Caractere
Intregi
Reale
Logice
Sir de caractere
-variabilele: retin date de un tip anume. O variabila isi poate schimba valoarea dar tipul nu.
O variabila pentru a fi prelucrata trebuie sa fie declarata (anuntata). Acest lucru consta de fapt in precizarea tipului variabilei.
Exemplu:
caracter car
intreg a
real b,c
logic x
sir y
- expresii: o expresie este alcatuita din unul sau mai multi operanzi legati intre ei prin operatori. Operanzii pot fi constante sau variabile.
Exemplu:
4.5+2*a
unde 4.4, 2, a sunt operanzi iar + si * sunt operatori
Expresiile pot interveni cel mai adesea in instructiuni de atribuire de tipul:
![]() variabila expresie
variabila expresie
Exemplu:
![]() c 2*b-1
c 2*b-1
Operatori pentru tipuri numerice :
|
operator |
semnificatie |
|
adunare |
|
|
scadere |
|
|
inmultire |
|
|
catul impartirii |
|
|
restul impartirii |
Operatori relationali :
|
operator |
semnificatie |
|
De egalitate |
|
|
<> |
diferit |
|
> |
Mai mare |
|
>= |
Mai mare sau egal |
|
< |
Mai mic |
|
<= |
Mai mic sau egal |
Operatori logici :
|
operator |
semnificatie |
|
Negatie logica |
|
|
si |
Si logic |
|
sau |
Sau logic |
Datele de tip logic pot avea doua valori : A (adevarat) si F (fals)
Reguli de compunere a operatorilor logici :
|
A |
F |
|
|
F |
A |
|
si |
A |
F |
|
A |
A |
F |
|
F |
F |
F |
|
sau |
A |
F |
|
A |
A |
A |
|
F |
A |
F |
Principiile programarii structurate
Programarea structurata a inceput la inceputul anilor 70. Este un concept cu o importanta fundamentala in scrierea algoritmilor.
In general, algoritmii se eleboreaza prin utilizarea exclusiva a anumitor structuri (liniara, alternativa, repetitiva).
Prin structura se intelege o anumita forma de imbinare a operatiilor cu care lucreaza algoritmii.
Structura liniara
Vom defini structura liniara astfel:
Daca S1, S2, S3,.Sn sunt structuri ( de orice tip), atunci:
S1
S2
S3
..
Sn
Constituie o strucura liniara reprezentata in pseudocod. Iar:

S2
![]()
![]() ..
..
Sn
Constituie o strucura liniara reprezentata in schema logica.
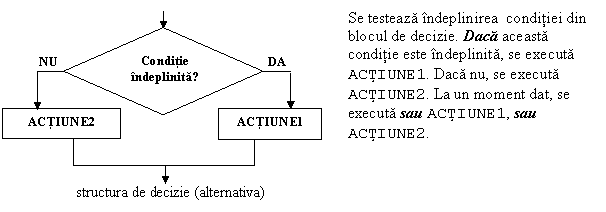 Structura alternativa
Structura alternativa
In pseudocod :
DACA conditie
ATUNCI actiune1
ALTFEL actiune2
Structura repetitiva
Figura
1.5. Structura repetitiva cu test
initial
Structuri repetitive cu test initial
Se evalueaza
conditia de test (figura 1.5.). Daca aceasta este indeplinita, se executa ACTIUNE1. Se revine apoi si se testeaza iar conditia. Daca este indeplinita, se
executa (se repeta) ACTIUNE1, s.a.m.d. Abia in momentul in care
conditia nu mai este indeplinita, se trece la executia ACTIUNE2 Astfel, cat timp conditia
este indeplinita, se repeta ACTIUNE1. In cazul in care, la prima testare a
conditiei, aceasta nu este indeplinita, se executa ACTIUNE2. Astfel,
este posibil ca ACTIUNE1 sa nu fie executata niciodata

Observatie : actiune2 este de fapt actiunea care urmeaza structurii repetitive motiv pentru care in pseudocod se poate scrie :
CAT TIMP conditie
REPETA actiune
Exisa si situatii in care se stie de la inceput de cate ori se va repeta o anumita actiune. In aceste cazuri se foloseste tot o structura de control repetitiva cu test initial. Se utilizeaza un contor (numeric) pentru a tine o evidenta a numarului de executii ale actiunii. De cate ori se executa actiunea, contorul este incrementat.

In pseudocod :
PENTRU contor=val_ini LA val_finala [PAS]
REPETA actiune;
Structura repetitiva cu test final:

In pseudocod :
REPETA actiune PANA CAND conditie
Grafuri neorientate
Graf neorientat= o pereche de multimi =(V, E)unde V este o multime finita nevida de elemente numite noduri iar E o multime de perechi neordonate din V, numite muchii. Notam graful cu G=(V, E).
Intr-un un graf G=(V, E) neorientat relatia binara este simetrica: (v,w)IE atunci (w,v) IE
Nod = element al multimii V, unde G=(V, E) este un graf neorientat.
Muchie = element al multimii E ce descrie o relatie existenta intre doua noduri din V, unde G=(V, E) este un graf neorientat;
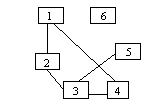
In figura alaturata:
V= sunt noduri
E= sunt muchii
G=(V, E)=(, )
Adiacenta: Intr-un graf neorientat existenta muchiei (v,w) presupune ca w este adiacent cu v si v adiacent cu w.
In exemplul din figura de mai sus varful 1 este adiacent cu 4 dar 1 si 3 nu reprezinta o pereche de varfuri adiacente.
Incidenta = o muchie este incidenta cu un nod daca il are pe acesta ca extremitate. Muchia (v,w) este incidenta in nodul v respectiv w.
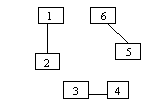
Grad = Gradul unui nod v, dintr-un graf neorientat, este un numar natural ce reprezinta numarul de noduri adiacente cu acesta (sau numarul de muchii incidente cu nodul respectiv)
Nod izolat = Un nod cu gradul 0.
Nod terminal un nod cu gradul 1
|
|
Nodul 5 este terminal (gradul 1). Nodul 6 este izolat (gradul 0) Nodurile 1, 2, 4 au gradele egale cu 2. |
Daca un graf neorientat are m muchii atunci suma gradelor tuturor nodurilor este 2m
In orice graf G exista un numar par de noduri de grad impar
Lant = este o secventa de noduri ale unui graf neorientat G=(V,E), cu proprietatea ca oricare doua noduri consecutive din secventa lant sunt adiacente:
L=[w1, w2, w3,. . ,wn] cu proprietatea ca (wi, wi+1)IE pentru 1£i<n.
Lungimea unui lant = numarul de muchii din care este format.
Lant simplu = lantul care contine numai muchii distincte
Lant compus= lantul care nu este format numai din muchii distincte
Lant elementar = lantul care contine numai noduri distincte
Ciclu = Un lant in care primul nod coincide cu ultimul.
Ciclul este elementar daca este format doar din noduri distincte, exceptie facand primul si ultimul. Lungimea unui ciclu nu poate fi 2.
|
|
Succesiunea de varfuri 2, 3, 5, 6 reprezinta un lant simplu si elementar de lungime 3. Lantul 5 3 4 5 6 este simplu dar nu este elementar. Lantul 5 3 4 5 3 2 este compus si nu este elementar. Lantul 3 4 5 3 reprezinta un ciclu elementar |
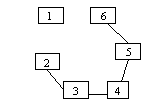
Graf partial = Daca dintr-un graf G=(V,E) se suprima cel putin o muchie atunci noul graf G'=(V,E'), E'Ì E se numeste graf partial al lui G (are aceleasi noduri si o parte din muchii).

Subgraf Daca dintr-un graf G=(V,E) se suprima cel putin un nod impreuna cu muchiile incidente lui, atunci noul graf G'=(V',E'), E'Ì E si V'ÌV se numeste subgraf al lui G.
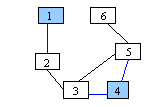
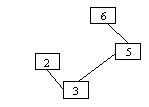
G G1 este subgraf al lui G
Graf regulat = graf neorientat in care toate nodurile au acelasi grad;
Graf complet = graf neorientat G=(V,E) in care exista muchie intre oricare doua noduri.
Numarul de muchii ale unui graf complet este: nr*(nr-1)/2.Unde nr este numarul de noduri
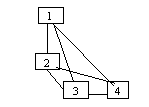 graf complet. Nr de muchii: 4x(4-1)/2
= 6
graf complet. Nr de muchii: 4x(4-1)/2
= 6
Graf conex = graf neorientat G=(V,E) in care pentru orice pereche de noduri (v,w) exista un lant care le uneste.
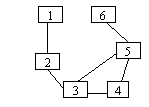 graf conex
graf conex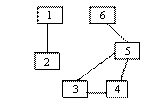 nu este graf conex
nu este graf conex
Componenta conexa = subgraf al grafului de referinta, maximal in raport cu proprietatea de conexitate (intre oricare doua varfuri exista lant);
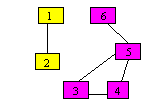 graful nu este conex. Are
2 componente conexe:
graful nu este conex. Are
2 componente conexe:
1, 2 si 3, 4, 5, 6
Lant hamiltonian = un lant elementar care contine toate nodurile unui graf
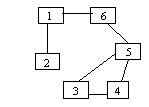 L=[2 ,1, 6, 5, 4,
3] este lant hamiltonian
L=[2 ,1, 6, 5, 4,
3] este lant hamiltonian
Ciclu hamiltonian = un ciclu elementar care contine toate nodurile grafului
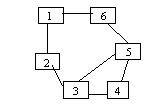 C=[1,2,3,4,5,6,1] este ciclu hamiltonian
C=[1,2,3,4,5,6,1] este ciclu hamiltonian
Graf hamiltonian = un graf G care contine un ciclu hamiltonian
Graful anterior este graf Hamiltonian.
Daca G este un graf cu n>=3 noduri astfel incat gradul fiecarui nod este mai mare sau egal decat n/2 atunci G este hamiltonian
Lant eulerian = un lant simplu care contine toate muchiile unui graf
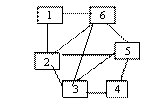
Lantul: L=[1.2.3.4.5.3.6.2.5.6] este lant eulerian
Ciclu eulerian = un ciclu simplu care contine toate muchiile grafului
Ciclul: C=[1.2.3.4.5.3.6.2.5.6.1] este ciclu eulerian
Graf eulerian = un graf care contine un ciclu eulerian.
Conditie necesara si suficienta: Un graf este eulerian daca si numai daca oricare varf al sau are gradul par.
Arbori
Definitia 1: Se numeste Arbore cu radacina = graf neorientat conex fara cicluri in care unul din noduri este desemnat ca radacina. Nodurile pot fi asezate pe niveluri incepand cu radacina care este plasata pe nivelul 1.
Radacina = Nod special care genereaza asezarea unui arbore pe niveluri; Aceasta operatie se efectueaza in functie de lungimea lanturilor prin care celelalte noduri sunt legate de radacina.
Descendent = intr-un arbore cu radacina nodul y este descendentul nodului x daca este situat pe un nivel mai mare decat nivelul lui x si exista un lant care le uneste si nu trece prin radacina.
Descendent direct / fiu = intr-un arbore cu radacina nodul y este fiul (descendentul direct) nodului x daca este situat pe nivelul imediat urmator nivelului lui x si exista muchie intre x si y.
Ascendent = intr-un arbore cu radacina nodul x este ascendentul nodului y daca este situat pe un nivel mai mic decat nivelul lui y si exista un lant care le uneste si nu trece prin radacina.
Ascendent direct / parinte = intr-un arbore cu radacina nodul x este parintele (ascendentul direct) nodului y daca este situat pe nivelul imediat superior (cu numar de ordine mai mic) nivelului lui y si exista muchie intre x si y.
Frati = intr-un arbore cu radacina nodul x este fratele nodului y daca au acelasi parinte.
Frunza intr-un arbore cu radacina nodul x este frunza daca nu are nici un descendent direct
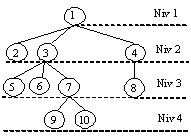
|
Arbore cu radacina |
- Nodul 1 este radacina. - Nodurile 5, 6, 7 sunt fii nodului 3. - Nodul 7 este parintele nodurilor 9 si 10; - Nodul 9 este descendentul lui 3 - Nodul 3 este ascendentul lui 10 - Nodurile 8, 9 si 10 sunt frunze - Nodurile 5, 6 si 7 sunt frati. |
Metode de memorare a arborilor
Cum un arbore este un caz particular de graf neorientat inseamna ca poate fi reprezentat ca un graf. De aici rezulta ca pentru reprezentarea unui arbore se pot utiliza:
Metode specifice grafurilor:
-matricea de adiacenta
-liste de adiacente
Metode specifice arborilor:
-prin legaturi de tip TATA. Arborele se reprezinta sub forma unui vector t cu n componente (n reprezinta numarul de noduri). Daca t[i]=k atunci nodul I este descendent al nodului k. Daca nodul I este varf atunci t[i]=0.
Fie arboreal din figura:
 unde nodul 1 este
radacina. Atunci vectorul de tip tata este:
unde nodul 1 este
radacina. Atunci vectorul de tip tata este:
Legatura de tip TATA se mai numeste si legatura cu referinte ascendente.
Legatura de tip TATA este determinata si de modul in care am ales nodul radacina. Spre exemplu daca vom considera nodul 4 ca fiind radacina vom obtine o alta solutie.
Metode de parcurgere:
Metodele de parcurgere sunt cele specifice grafurilor: in adancime si in latime.
TABLOURI UNIDIMENSIONALE
DECLARAREA TABLOURILOR
Numim tablou o colectie (grup, multime ordonata) de date, de acelasi tip, situate intr-o zona de memorie continua (elementele tabloului se afla la adrese succesive). Tablourile sunt variabile compuse (structurate), deoarece grupeaza mai multe elemente. Variabilele tablou au nume, iar tipul tabloului este dat de tipul elementelor sale. Elementele tabloului pot fi referite prin numele tabloului si indicii (numere intregi) care reprezinta pozitia elementului in cadrul tabloului.
In functie de numarul indicilor utilizati pentru a referi elementele tabloului, putem intalni tablouri unidimensionale (vectorii) sau multidimensionale (matricile sunt tablouri bidimensionale).
Ca si variabilele simple, variabilele tablou trebuie declarate inainte de utilizare.
Modul de declarare:
tip nume_tablou[dim_1][dim_2].[dim_n];
unde: tip reprezinta tipul elementelor tabloului; dim_1,dim_2,,dim_n sunt numere intregi sau expresii constante intregi (a caror valoare este evaluata la compilare) care reprezinta limitele superioare ale indicilor tabloului.
TABLOURI UNIDIMENSIONALE
Tablourile unidimensionale sunt tablouri cu un singur indice (vectori).
Daca tabloul contine dim elemente, indicii elementelor au valori intregi din intervalul [0, dim-1]
Un element al unui tablou poate fi utilizat ca orice alta variabila. Adresarea unei componente se face proin indicele ei, trecut intre paranteze drepte. Se pot efectua operatii asupra fiecarui element al tabloului, nu asupra intregului tablou.
Exemple:
int vect[20]; /* declararea tabloului vect, de maximum 20 de elemente, de tipul int. Elementele tabloului vect sunt : vect[0], vect[1], ., vect[19] - date de tip int*/
double p,q,tab[10]; // declararea variabilelor simple p, q si a vectorului tab de maximum 10 elemente, tip double
#define MAX 10
char tab[MAX]; /*declararea tabloului tab, de maximum MAX (10) elemente de tip char*/
Consideram declaratia tabloului v cu maxim 6 elemente de tip int
int v[6];
Elementele tabloului pot fi initializate prin atribuire:
v[0]=100;
v[1]=101;
v[2]=102;
v[3]=103;
v[4]=104;
v[5]=105;
|
v[0] |
v[1] |
v[2] |
v[3] |
v[4] |
v[5] |
Exemplu:
double alpha[5], beta[5], gama[5];
int i=2;
alpha[2*i-1] = 5.78;
alpha[0]=2*beta[i]+3.5;
gama[i]=aplha[i]+beta[i]; //permis
gama=alpha+beta; //nepermis
Variabilele tablou pot fi initializate in momentul declararii:
declaratie_tablou=lista_valori;
Valorile din lista de valori sunt separate prin virgula, iar intreaga lista este inclusa intre acolade:
Exemple:
int v[6]=;
double x=9.8;
double a[5]=;
La declararea unui vector cu initializarea elementelor sale, numarul maxim de elemente ale tabloului poate fi omis, caz in care compilatorul determina automat marimea tabloului, in functie de numarul elementelor initializate.
Exemplu:
char tab[]=;
![]()
[0] [3]
float data[5]=;
![]()
[0] [4]
Citirea elementelor unui vector:
double a[5];
int i;
for (i=0; i<5; i++)
Sau, pentru un vector cu n componente (n£
double a[20]; int i, n;
cout<<"Dim. Max. ="; cin>>n;
for (i=0; i<n; i++)
Pentru simplitate, se pot considera elementele vectorului incepand cu pozitia 1. In acest caz, primul element al tabloului ramane neutilizat, iar valoarea sa este cea alocata implicit la compilare.
double a[20]; int i, n;
cout<<"Dim. Max. ="; cin>>n;
for (i=1; i<=n; i++)
Afisarea elementelor unui vector:
cout<<"Vectorul introdus este:n
for (i=0; i<n i++)
cout<<a[i]<<' ';
PROBLEME
In schema logica si program
Probleme de logica:
PL1-pg250
Doi prieteni,Mircea si Dan dupa cursul de matematica s-au dus la bar.Brusc,Mircea l-a intrebat pe Dan:
Cat de mare este numarul cifrelor in suma numarului cifrelor din suma numarului de cifre in 4444la puterea4444?
-Oh!trebuie sa fie foarte mare,spuse Dan.
-Nu cred.Voi cumpara atatea cutii de bere pentru tine.
-Nu glumi,nu poti fi atat de bogat.Dar, oricum!
-Hai,imi pot permite 50000 de lei pentru asta!
-OK!S-a facut!
Cate cutii de bere a cumoarat Mircea?
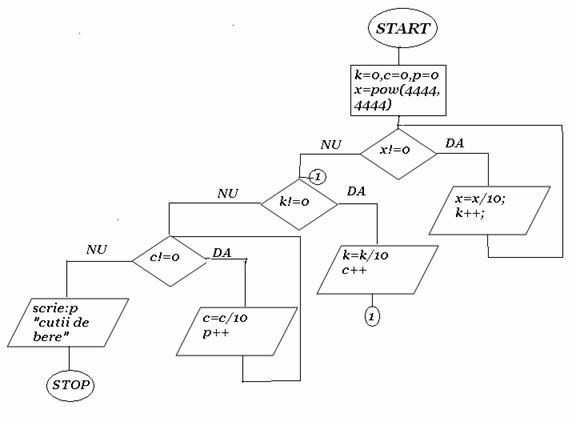
#include<conio.h>
#include<iostream.h>
#include<math.h>
void main()
while(k!=0)
while(c!=0)
cout<<'a cumparat'<<p<<'cutii de bere';
getch();
Pl6-pg252
Am gasit doua numere:unul de trei cifre si altul de doua cifre.Daca impartim A la B catul rezultat este egal cu suma cifrelor divizorului,iar in restul este un numar de doua cifre constand din cifrele divizorului in ordine inversa.Daca se inmulteste restul cu catul si apoi se incrementeaza cu divizorul,atunci numarul de trei cifre obtinut va consta din cifrele deimpartitului in ordine inversa.
Gasiti numerele A si B.
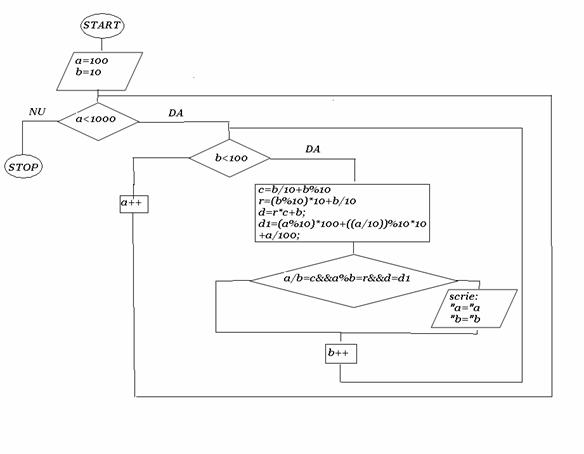
#include<conio.h>
#include<iostream.h>
void main()
getch();
Alte probleme
O matrice m*n cu m studenti si n discipline.Matricea contine notele studentilor.Sa se determine:
a)studentii integralisti(notele>=5)
b)studentii bursieri(media>=8)
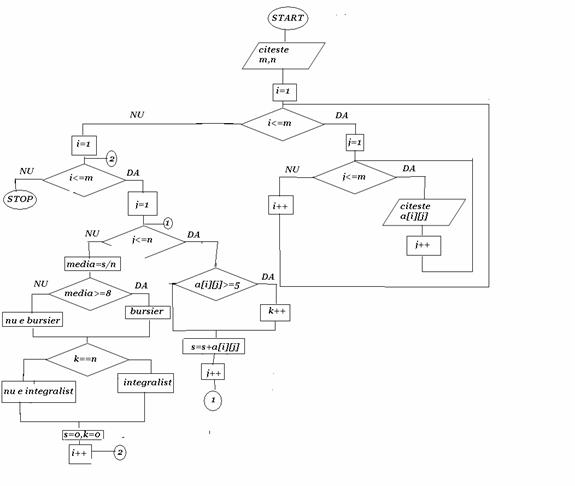
#include<conio.h>
#include<iostream.h>
#include<string.h>
void main()
media=s/n;
if(media>=8)
cout<<'studentul'<<i<<'este bursier'<<endl;
else
cout<<'studentul'<<i<<'nu este bursier'<<endl;
if(k==n)
cout<<'studentul '<<i<<'este integralist'<<endl;
else
cout<<'studentul '<<i<<' nu este integralist'<<endl;
s=0;k=0;
}
getch();
Sa se construiasca o matrica astfel incat pe diagonala principala sa fie valoarea 0, in zona de deasupra diagonalei principale sa fie valoarea liniei iar in zona de dedesuptul diagonalei principale sa fie valoarea coloanei.
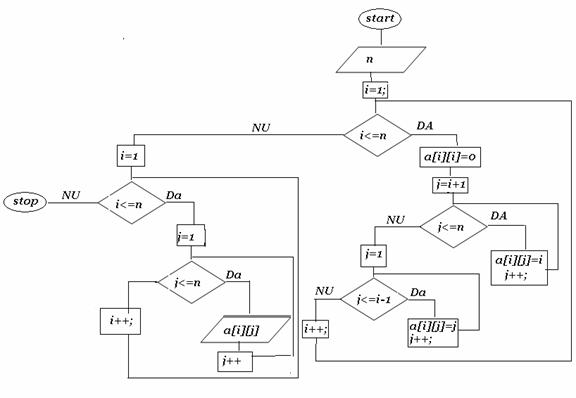
void main()
for(i=1;i<=n;i++)
getch();
Se da un numar n cu maximum 9 cifre si k prin care se primeste un numar natural (k<=9).Sa se modifoce numarul n astfel incat primele k cifre din n de la stanga sa ajunga ultimele cifre ale lui n.Sa se afiseze numarul astfel obtinut.
Exemplu:
n=
k=4 deci numarul 7462 va trece la coada lui n.Se va afisa numarul 934
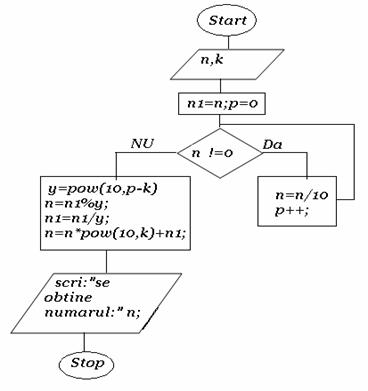
#include<conio.h>
#include<iostream.h>
#include<math.h>
void main()
int y=pow(10,p-k);
n=n1%y;
n1=n1/y;
n=n*pow(10,k)+n1;
cout<<"se obtine numarul" <<n;
getch();
A fost odata un taran sarac.Intr-o zi el a gasit o samanta.A pus-o in pamant, si minune:dupa ce a rasarit a inceput sa creasca in inaltime,in fiecare zi cate un metru!Dupa doua zile apare un mugur cu o noua ramura si apoi in fiecare zi mai apare cate o ramura.Fiecare ramura noua creste si inmugureste la fel ca prima.Dupa cateva zile taranul taie planta si are dificultati in a numara ramurile si a masura lungimea lor totala.
Taranul va roaga sa-il ajutati:el va spune numarul de zile dupa care a taiat planta si voi sa ii spuneti cate ramuri are si ce lungime totala obtine daca ar pune cap la cap toate ramurile?
Exemplu:dupa 5 zile planta are 4 ramuri totalizand 12 metrii.(problema din cartea de Algoritmi si structuri de date, pagina 261, problema 6)
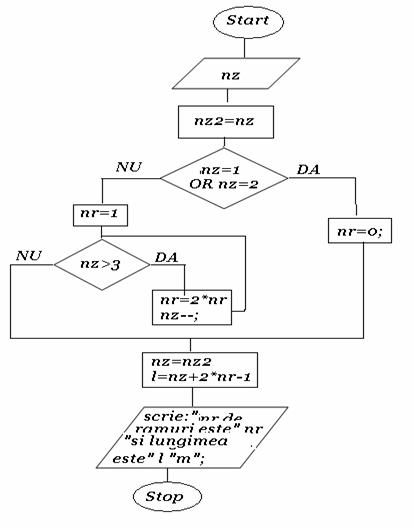
#include<conio.h>
#include<iostream.h>
void main()
}
nz=nz2;
l=nz+2*nr-1;
cout<<'numarul de ramuri este '<<nr<<' si lungimea totala a plantei este de ' <<l<<"m";
getch();
Sa se interschimbe elementele unui vector astfel incat primul element sa fie ultimul, al doilea element sa fie penultimul, al treilea sa fie antepenultimul etc.
Exemplu:
Vectorul v=(1,2,3,4,5) cu 5 elemnte va fi v=(5,4,3,2,1);
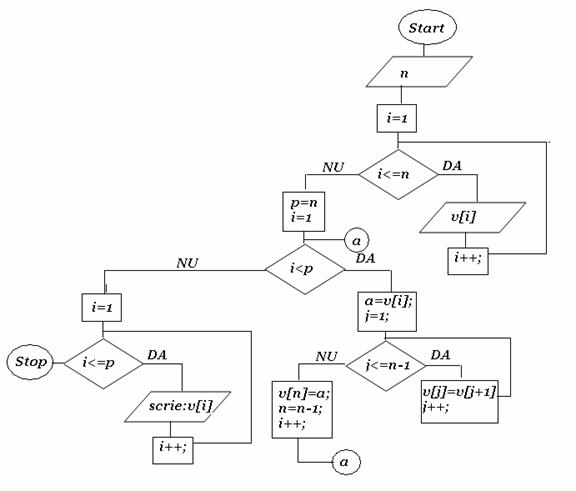
#include<conio.h>
#include<iostream.h>
void main()
for(i=1;i<=p;i++)
cout<<v[i]<<' ';
getch();
Sa se scrie un program care citeste o matrice si calculeaza apoi suma elementelor fiecarei linii pe care o depune apoi intr-un vector avand un numar de elemente egal cu numarul de linii.
Operatia de gasire a max in vectorul astfel obtinut,sa se afiseze numarul liniei care prezinta suma maxima si valoarea respective.
|