PROIECTAREA SI REALIZAREA SISTEMELOR EXPERT BAZATE PE CUNOASTERE

PROIECTAREA SI REALIZAREA SISTEMELOR EXPERT BAZATE PE CUNOASTERE

In acest capitol prezint principalele modele ale sistemelor expert bazate pe cunoastere. Voi face o clasificare a acestor modele si voi insista asupra unora dintre ele. Vor urma definitiile termenului de "sistem expert" in viziunea unor cercetatori din domeniu si se vor trage concluziile principale. De asemenea, voi preciza obiectivul de baza al sistemelor expert, conturand structura lor si ma voi opri asupra a doua dintre componentele lor principale.

2.1 Definirea Sistemelor Expert

Definitiile sistemelor expert sunt numeroase si in marea majoritate se identifica aspectul functional al acestora.

In viziunea unor cercetatori ele sunt definite astfel:

"Sistemele expert sunt programe concepute pentru a rationa in scopul rezolvarii problemelor pentru care in mod obisnuit se cere o expertiza umana impresionanta" (Edward Feigenbaum de la Stanford University);

"Sistemul expert este un program particular care incorporeaza o baza de cunostinte si un motor de inferente. Programul se comporta ca un consilier inteligent intr-un domeniu particular." (Louis E. Frenzel);

"Un sistem expert este un sistem care emuleaza abilitatea de a lua decizii a expertului uman. Termenul "emuleaza" inseamna ca sistemul este menit sa actioneze in toate privintele ca expertul uman. Emularea este ceva mai mult decat simularea, care cere sa se actioneze prin imitarea conditiilor realizate. Sistemele expert actioneaza foarte bine in domenii bine delimitate." (J. Giarratano si G. Riley de la NASA);

"Sistemele expert sunt programe, dar pot fi tot atat de bine masini cu software, destinate sa inlocuiasca sau sa asiste specialistul in domeniile unde este recunoscuta necesitatea expertizei umane." (Farreny H.);

"Sistemul expert este un produs program care emuleaza comportamentul expertilor umani care rezolva probleme din lumea reala asociate unui domeniu particular al cunoasterii." (P.V. Pigford si G. Baur).

Daca analizam aceste definitii putem sa desprindem concluzia ca ideile de baza ale sistemelor expert sunt urmatoarele:

Din punct de vedere conceptual, sistemele expert au ca scop reconstituirea rationamentului uman pe baza expertizei obtinuta de la experti

Sistemele expert au comportamentul unui "asistent inteligent", ele dispunand de metode de invocare a cunoasterii si exprimare a expertizei

Sistemele expert dispun de cunostinte si de capacitatea de a desfasura activitati intelectuale umane

Sistemele expert au posibilitatea de a memora cunostinte, de a stabili legaturi intre acestea si de a infera concluzii, solutii, recomandari;

Sistemele expert achizitioneaza si utilizeaza cunoasterea intr-un domeniu particular foarte bine delimitat

Sistemele expert se bazeaza pe separarea cunoasterii (baza de cunostinte) de programul care o trateaza (motorul inferential)

In prezent, dezvoltarea sistemelor expert cunoaste patru directii de orientare :

Medii si instrumente generale pentru sisteme expert;

Medii si instrumente specifice problemei ;

Medii si instrumente specifice domeniului ;

Limbaje de programare si instrumente pentru ajutor in programare;

Pentru dezvoltarea sistemelor expert au fost create medii si instrumente specializate, precum si limbaje de Inteligenta Artificiala. Astfel apare o diferentiere intre limbajele neprocedurale si limbajele procedurale.

Limbajele neprocedurale se impart in limbaje declarative, din care fac parte limbajele orientate pe obiect, modelele logice, modelele bazate pe reguli si modelele bazate pe cadre, si in limbaje nedeclarative, din care fac parte modelele bazate pe inductie (figura 2.1).

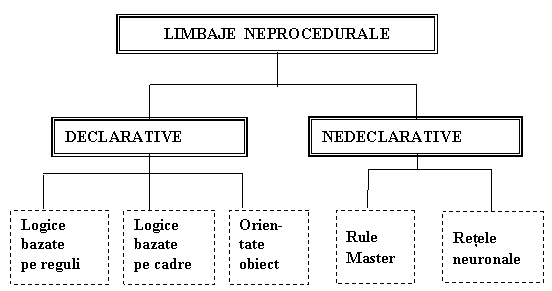
Figura 2.1 - Clasificarea limbajelor neprocedurale

Limbajele procedurale se impart in limbaje imperative, din care fac parte limbajele Ada, Pascal, C, etc., si limbajele functionale, din care fac parte LISP, APL, etc. (figura 2.2).

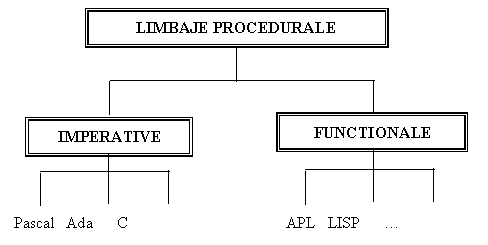
Figura 2.2 - Clasificarea limbajelor procedurale

2.2 Tipuri de problemele rezolvate de Sistemele Expert

Sistemele Expert au fost concepute astfel incat sa poata rezolva tipuri de probleme extrem de variate, insa activitatile de baza ale acestor sisteme sunt enumerate si comentate mai jos.

Majoritatea Sistemelor Expert executa mai mult de una din aceste activitati. De exemplu, diagnosticul se desfasoara de multe ori impreuna cu conceptia si instruirea, supravegherea impreuna cu controlul si dirijarea iar previziunea impreuna cu planificarea. Consecutiv, cercetatorii AI gasesc utila categorisirea Sistemelor Expert in functie de tipul de probleme pe care acestea le rezolva sau dupa tipul domeniilor de inferenta. Dintre aceste domenii unul din cele mai populare pare sa fie medicina, avand in vedere ca cele mai multe sisteme expert au fost dezvoltate pentru medicina decat pentru oricare altul dintre domeniile de activitate.

Activitatile de baza ale Sistemelor expert sunt: interpretare; diagnostic; planificare; conceptie (proiectare); control si dirijare; previziune; simulare;supraveghere; formare (instruire).

Descrierea sumara a acestor activitati este urmatoarea:

de interpretare - se refera la traducerea unor semnale care provin prin captari de exemple sau de date primare in expresii simbolice care pot fi folosite in rationamente;

de diagnostic se refera la stabilirea unei corelatii intre caracteristici sau simptome si situatii tip;

de planificare se refera la definirea in timp si in spatiu a unor actiuni care permit atingerea unor stari finale prin compararea starii curente cu cea dorita luand in consideratie consecintele de actiune astfel incat sa se permita respectarea restrictiilor impuse de mediu, de nivelul resurselor disponibile si de consecintele previzibile de interactiune dintre stari si actiuni sau dintre stari succesive;

de conceptie (proiectare) - se refera la multitudinea de alegeri si de decizii care permit determinarea unui caiet de sarcini care trebuie indeplinit pentru un anumit obiectiv luand in considerare anumite performante, eventual fixate pe baza unui diagnostic. In functie de necesitatile exprimate la un moment dat sunt furnizate mijloacele pentru a se atinge acel obiectiv prin definirea unor specificatori ai unui produs sau unui proces care respecta caietul de sarcini;

de control si dirijare - se refera la multimea de actiuni care se aplica unui sistem pe baza unor informatii ce rezulta din supravegherea sistemului si din anticiparea unor situatii care sa permita o intretinere permanenta si un raspuns adaptat la diferite situatii de functionare a sistemului;

de previziune se refera la descrierea unei situatii de anticipare, plecand de la o situatie curenta prin intermediul unui model conceput pe baze de date statistice sau prin invatare;

de simulare se refera la obtinerea deductiilor plecand de la un model al consecintelor de actiune sau evenimente declansate in cursul derularii actiunii de simulare;

de supraveghere se refera la declansarea unei alarme in conditii determinate care pot sa evolueze odata cu contextul sau sa se trimita o dare de seama plecand de la semnale interpretate si folosite intr-un diagnostic;

de formare-instruire se refera la transmiterea de cunostinte unei persoane. Aceasta transmitere de cunostinte, "de a sti" in sensul de a avea cunostinte sau "de a sti sa faci" se poate folosi ulterior pentru un diagnostic, o intretinere, o conceptie.

2.3 Tipologia Sistemelor Expert

Sistemele Expert prezinta o mare diversitate de tipuri. O clasificare completa si corecta din toate punctele de vedere este foarte greu de facut. Exista totusi cateva criterii dupa care s-ar putea clasifica:

natura cunostintelor;

caracteristicile cunoasterii memorate sau metode de reprezentare a cunoasterii ;

natura problemelor pe care le solutioneaza sau domeniul aplicativ ;

strategiile de control si metodele de inferenta .

In functie de natura cunostintelor reprezentate sistemele expert se impart in:

Sisteme Expert Bazate pe Reguli - sunt cele mai numeroase, deoarece tehnologia lor este cel mai bine organizata;

Sisteme Expert Bazate pe Cadre - au cunoasterea reprezentata sub forma unor cadre (obiecte structurate) si folosesc reprezentari specifice programarii orientate pe obiect;

Sisteme Hibride - includ cateva metode de reprezentare a cunoasterii, cel putin reguli si cadre. Aceasta reprezentare este specifica Sistemelor Multiexpert;

Sisteme Bazate pe Modele - sunt construite in jurul unui model pentru simularea structurii si functionarii unui sistem aflat in studiu.

Din punct de vedere al naturii problemelor rezolvate sistemele expert se impart in:

Sisteme Expert cu Colectarea Faptelor Doveditoare (Evidentelor) - sunt foarte importante in orice tip de expertiza: contabila, tehnica, medicala, etc.;

Sisteme Expert cu Rafinare in Pasi Succesivi - au un numar mare de iesiri obtinute prin detalierea succesiva pe niveluri a problemei din domeniu;

Sisteme Expert cu Asamblare in Pasi Succesivi - numeroasele iesiri ale sistemului au legatura cu o gama larga de rezultate posibile;

Sistemele Expert "la Cheie" - sunt realizate pentru nevoile unui utilizator particular. Ele pot fi cumparate ca orice produs-program si au o natura foarte generala.

Sisteme Expert in Timp Real - in cadrul acestor sisteme timpul de raspuns are o limita stricta, suficienta pentru controlul proceselor.

Se poate face si un alt tip de impartire a Sistemelor Expert, in functie de categoria de utilizatori. Se deosebesc, astfel, trei grupe:

Sisteme Expert de Clasa I - sunt deja comercializate si acceptate de catre utilizatori. Domeniile de aplicabilitate sunt diverse si interactioneaza doar cu utilizatorii carora le ofera solutii concrete. Aceste sisteme isi explica operatiile si accepta un minimum de imprecizie;

Sisteme Expert de Clasa II - au performante de expert, dar nu si-au castigat in totalitate renumele in randul utilizatorilor. In aceasta categorie intra sistemele pentru consultanta sau diagnostic, care nu-si explica suficient de bine comportamentul, nu dispun de expertiza suficienta ori diagnosticul pe care il ofera nu este inca acceptabil;

Sisteme Expert de Clasa III - sunt sisteme care nu au ajuns la performante de expert, fie din cauza domeniului aplicativ foarte complex, fie din cauza multor greseli obtinute in activitatea lor. In aceasta clasa intra sistemele pentru intelegerea vorbirii si din domeniul cercetarii matematice.

O clasificare dupa criteriul organizational al sistemelor expert, este abordata de unii autori obtinand doua grupe :

Sisteme Expert Interne si Sisteme Expert Externe

Sisteme consultante, Sisteme Expert si Sisteme expert de transfer al expertizei

2.4 Structura sistemelor expert

Notiunea de Sistem Expert este folosita in aceleasi imprejurari cu cea de "Sistem Bazat pe Cunostinte", desi aceasta din urma este considerata un domeniu mult mai general deoarece nu se refera numai la domeniul Inteligentei Artificiale. In literatura de specialitate apar unele deosebiri din punct de vedere al detaliilor constructive si al functionalitatii.

Componenta principala a prelucrarii inteligente este reprezentata de rationamentul artificial, capabil de a imita rationamentul uman. Asemeni expertilor umani, Sistemele Expert folosesc cunostintele puse la dispozitia lor, le multiplica si ofera explicatia rationamentului urmat.

Analogia dintre un expert uman si un Sistem Expert poate fi mai sugestiv reprezentata in figura 2.3.

Pentru relevarea relatiei cu sistemele de Inteligenta Artificiala este suficienta observarea figurii 2.4. care indica in mod clar ca si acestea prelucreaza cunoasterea organizata in baze de cunostinte.

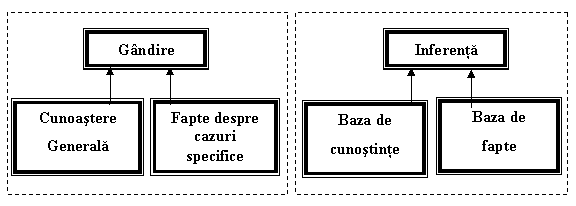
EXPERT UMAN SISTEM EXPERT

Figura 2.3 - Asemanarea dintre expertul uman si sistemul expert

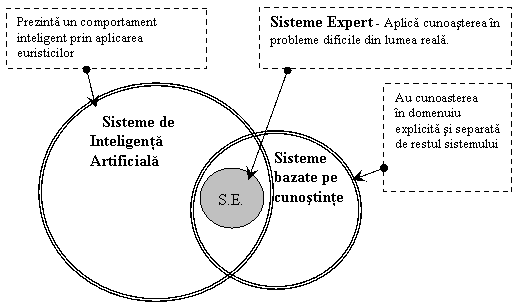
Figura 2.4 - Relatia Sistem Expert - Sisteme de inteligenta artificiala - Sisteme bazate pe cunostinte

Intr-un sistem expert cunoasterea este organizata in asa fel incat sa separe cunostintele referitore la domeniul problemei de alte tipuri de cunostinte, cum sunt cele despre rezolvarea problemei si cele despre interactiunea cu utilizatorul. Din acest motiv s-au introdus termenii:

baza de cunostinte pentru colectia de cunostinte despre domeniul problemei;

baza de fapte reprezinta faptele initiale care descriu enuntul problemei de rezolvat.

motor inferential pentru cunoasterea despre modul de rezolvare a problemei;

interfata de dialog pentru cunoasterea despre interactiunea cu utilizatorul.

Modul in care sistemul expert utilizeaza cunostintele cu care este dotat prezinta o importanta deosebita intrucat un sistem expert trebuie sa dispuna atat de cunostinte, cat si de mijloacele de utilizare efectiva a cunostintelor pentru a putea fi considerat suficient de calificat intr-un domeniu.

Structura sistem expert trebuie sa contina cel putin trei module principale care formeaza asa numitul sistem esential si altele:

O baza de cunostinte pentru colectia de cunostinte despre domeniul problemei de rezolvat;

Un motor de inferente pentru cunoasterea modului de rezolvare a problemei;

baza de fapte - memorie auxiliara care contine toate datele utilizatorului si rezultatele intermediare produse de cursul rationamentului.

Modulul explicativ care furnizeaza explicatii referitoare la rationamentul folosit in obtinerea solutiei;

Modulul de achizitie preia cunostintele specializate furnizate de expertul uman prin intermediul cogniticianului intr-o forma nespecifica reprezentarii interne;

Interfata de dialog cu utilizatorul.

Cele trei componente de baza cat si relatiile existente intre ele sunt reprezentate in figura 2.5.

Baza de cunostinte

Baza de cunostinte este formata din ansamblul cunostintelor specializate introduse de expertul uman. Cunostintele stocate aici sunt in principal descrierile obiectelor si a relatiilor dintre acestea. Baza de date face parte din sistemul cognitiv, cunoasterea fiind memorata intr-un spatiu special organizat. Forma de stocare trebuie sa asigure cautarea cunostintelor specificate direct prin simboluri identificatoare sau indirect prin proprietati asociate sau inferente care pornesc de la alte cunostinte.

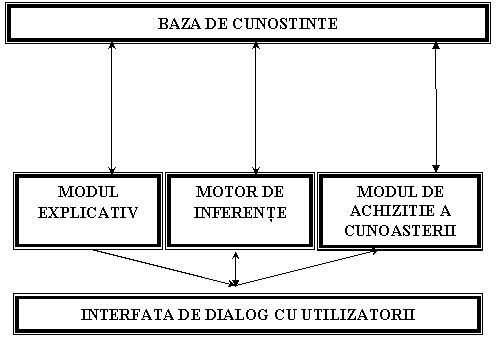
Figura 2.5 - Structura sistemelor expert

Motorul inferential

Motorul inferential este un program care dispune de mecanisme inferentiale generale pentru prelucrarea cunostintelor, ducand la modificarea cunoasterii cu scopul de a rezolva problema. Mecanismul de inferenta urmareste o serie de obiective majore, cum ar fi: alegerea strategiei de control in functie de problema curenta, elaborarea planului de rezolvare a problemei dupa necesitati, comutarea de la o strategie de control la alta, executarea actiunilor prevazute in planul de rezolvare.

Modulul explicativ

Modulul explicativ, prezent in cazul sistemelor expert complexe, are scopul de a obtine explicatii asupra desfasurarii proceselor inferentiale, asupra solutiilor obtinute in sesiunile de consultare si evidentiere a unor cunostinte care lipsesc sau sunt inconsistente.

Daca sistemul expert este un concept relativ usor de inteles, alta este situatia in cazul in care se doreste realizarea unui astfel de sistem. Complexitatea crearii unui Sistem Expert implica doua activitati esentiale si dificile in acelasi timp:

Extragerea cunoasterii de la experti impreuna cu metodele utilizate de catre acestia in solutionarea problemelor

Reformularea (transformarea) cunoasterii si a metodelor intr-o forma organizata, cunoscuta sub denumirea de reprezentarea cunoasterii, in vederea utilizarii lor ulterioare

Aceste doua activitati sunt parti componente a celui mai complex element al Sistemelor Expert, modulul de achizitie si reprezentare a cunoasterii, si poarta denumirea de ingineria cunoasterii.

Termenul de euristica inseamna a inventa, a descoperi. O gandire euristica implica mai multe procese: judecata, cautare, reinvatare, evaluare si exploatare. Cunoasterea obtinuta in urma acestei serii de procese poate la randul ei modifica procesul de cautare in vederea solutionarii problemelor.

In cazul proceselor inferentiale este utilizat rationamentul care include deductia, inductia si abductia (determinarea scopului). Pe baza expertizei memorate in baza de cunostinte si a programului, care poate sa aiba acces la o baza de date sau la un fisier, calculatorul este programat sa faca inferente. Aceste inferente sunt efectuate de un motor inferential care detine proceduri si cunoastere procedurala in ceea ce priveste solutionarea problemei. Daca pana acum majoritatea sistemelor expert se bazau pe reguli de productie de forma IF . THEN . ELSE (DACA . ATUNCI . ALTFEL) memorate in baza de cunostinte, mai recent metoda frame-urilor (cadrelor) a venit in completarea acestei reprezentari.

Expertiza reprezinta o cunoastere intensiva, specifica domeniului problemei, dobandita prin instruire, citire sau experienta indelungata.

Expertiza include

Fapte despre domeniul problemei;

Teorii din domeniul problemei;

Reguli si proceduri privind domeniul problemei;

Reguli sau euristici despre ceea ce trebuie facut intr-o situatie problematica data, pentru rezolvarea problemei;

Strategii globale despre rezolvarea tipurilor de probleme;

Metacunoastere (cunoastere despre cunoastere).

Interfata de dialog

Interfata de dialog permite utilizatorilor experti accesul la faptele si cunostintele din baza de cunostinte, iar utilizatorilor beneficiari ai serviciilor acestui sistem expert le este permis dialogul cu ceilalti utilizatori in timpul sesiunii de consultare.

Transferul expertizei de la expertul uman la calculator inapoi la utilizatorul expert sau obisnuit constituie obiectivul de baza al unui Sistem Expert. Procesul acesta include cateva etape:

Achizitionarea cunostintelor printr-o exprimare cat mai corect posibila a expertizei obtinute de la expertul uman (reprezentarea cunoasterii in calculator);

Exploatarea eficienta a relatiei dintre cunostinte (inferentierea pe baza cunoasterii stocate);

Transferul cunoasterii catre utilizator

Suportul complet in ceea ce priveste controlul operatiilor ce se pot efectua asupra cunostintelor (adaugarea, modificarea si eliminarea lor).

Motorul Inferential

Inima oricarui sistem expert este reprezentata de motorul inferential, de aceea este necesar sa se cunoasca principiile de functionare interne ale acestuia.

Fiecare motor de inferente are un ciclu de baza, o strategie de cautare si strategii de control al rationamentelor. Cum cele mai des utilizate sisteme expert sunt cele care se bazeaza pe reguli, voi prezenta in continuare principiul de functionare al motorului inferential prezent intr-un astfel de sistem.

Ciclul de baza al unui motor inferential cuprinde intotdeauna patru faze (figura 2.6), indiferent de strategia de control al rationamentelor:

Restrictia ;

Filtrarea ;

Rezolvarea conflictelor ;

Executia .

Restrictia are scopul de a obtine un subansamblu de fapte si un subansamblu de reguli din baza de cunostinte, care merita toata atentia in vederea executiei in raport cu celelalte . Aceasta faza mai poarta denumirea si de selectie.

Filtrarea este urmatoarea faza in care se compara partea de premisa din regulile selectate in faza anterioara cu faptele selectate anterior, pentru a determina un subansamblu de reguli declansabile numit subansamblu de conflict. Regulile acestui subansamblu intra in competitie si in urma acestei lupte numai o regula va fi executata efectiv.

Rezolvarea conflictelor este chiar alegerea regulii care va fi executata. In aceasta faza se pot utiliza mai multe strategii:

Prima regula din lista ;

Regula cea mai putin complexa ;

Regula cea mai putin utilizata ;

Regula cea mai specifica, etc.

Executia consta in activarea regulii obtinuta din faza anterioara, actiune care va avea ca efect, in general, adaugarea unuia sau mai multor fapte in baza de cunostinte. Daca dupa faza de rezolvare a conflictelor nu se reuseste alegerea nici unei reguli, procesul inferential este oprit sau poate fi reluat de la faza de filtrare, cautandu-se declansarea altor reguli.

In practica, fiecare faza a ciclului de baza al motorului inferential are o structura proprie, dar nu unica, iar rezolvarea unei probleme necesita inlantuirea automata a mai multor astfel de cicluri de baza.

Din descrierea mecanismului inferential de mai sus se poate concluziona o caracteristica a sistemelor expert bazate pe reguli, si anume : comunicarea intre reguli se realizeaza numai prin intermediul bazei de fapte.

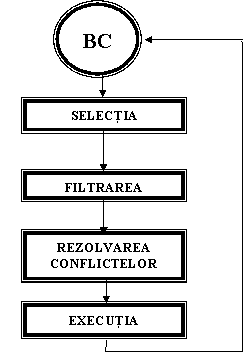
Figura 2.6 - Fazele ciclului de functionare ale motorului inferential

unde BC = Baza de Cunostinte

Motorul inferential bazat pe reguli indeplineste urmatoarele functii:

Activeaza (declanseaza) regulile;

Adreseaza utilizatorului o intrebare;

Adauga raspunsul utilizatorului in baza de fapte;

Infereaza un nou fapt dintr-o regula;

Adauga faptul inferat in baza de fapte;

Compara faptele din baza de fapte cu componentele corespunzatoare din reguli;

Daca sunt potriviri, regulile se declanseaza;

Daca mai sunt si alte asemanari, controleaza daca scopul prestabilit este atins;

Declanseaza cel mai mic numar de reguli necesare rezolvarii problemei.

Motorul inferential lucreaza cu baza de cunostinte pana cand fixeaza un fapt din baza de fapte sau doar un fapt partial daca se lucreaza cu incertitudine. Dupa ce faptele au fost introduse in baza de fapte, motorul trece din nou la baza de cunostinte pentru a infera alte fapte. Acest proces se va repeta pana in momentul in care scopul prestabilit este atins sau pana cand toate regulile au fost declansate si a rezultat un esec.

Motorul inferential mai prezinta doua functii:

Sistemul de administrare a bazei de cunostinte;

Procesorul de inferente simbolic.

Sistemul de administrare a bazei de cunostinte realizeaza operatii de organizare automata, control si actualizare a cunostintelor, initializeaza cautari pentru controlul relevantei pe caile de rationament pe care lucreaza procesorul de inferente simbolic.

Procesorul de inferente simbolic ofera o metoda de prelucrare prin care se furnizeaza liniile de rationament. Daca datele si cunostintele din lumea reala sunt imprecise, anumite metode de inferenta pot utiliza diferite grade de certitudine pentru derularea mecanismului inferential.

Baza de cunostinte

Dupa cum am mai aratat, baza de cunostinte este una dintre componentele de baza ale unui sistem expert. In ea se gasesc cunostintele despre problema ce se doreste a fi rezolvata, faptele si regulile care ofera motorului inferential suportul pentru inferentele realizate.

Construirea unei baze de cunostinte implica un efort deosebit in realizarea sistemului expert. Aceasta responsabilitate ii revine cogniticianului, care trebuie sa se ocupe de achizitionarea si organizarea cunoasterii.

Achizitia cunoasterii este procesul de colectare, structurare si organizare a cunoasterii, din una sau mai multe surse (documente sau experti). Scopul acestei achizitii este acela de a o depozita cunoasterea in baza de cunostinte a sistemelor expert si de a o folosi la rezolvarea problemelor din cele mai diverse domenii aplicative.

Achizitia cunoasterii este una din cele cinci activitati de baza in dezvoltarea sistemelor expert (vezi figura 2.7), alaturi de validarea, reprezentarea, inferentierea si explicarea sau justificarea inferentelor.

Achizitia cunoasterii presupune informarea cogniticianului de la expertul domeniului din care face parte problema si/sau strangerea de informatii din documente referitoare la acea problema.

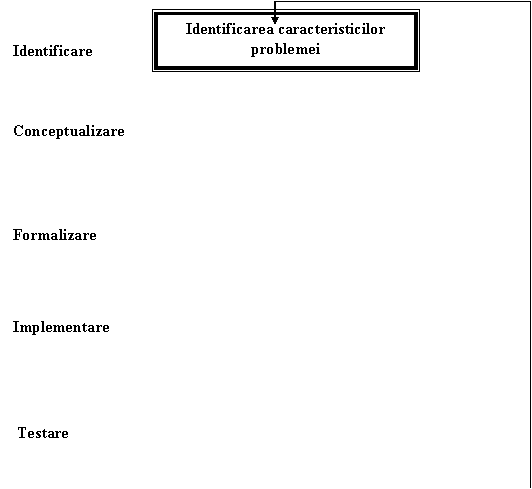
Acest proces de achizitie a cunoasterii are cinci faze (figura 2.8):

identificarea;

conceptualizarea;

formalizarea;

implementarea si testarea.

Fazele sunt interdependente, uneori suprapuse, iar deosebirea dintre ele nu este usor de facut deoarece in timpul construirii sistemului expert cogniticianul poate fi implicat in oricare dintre ele.

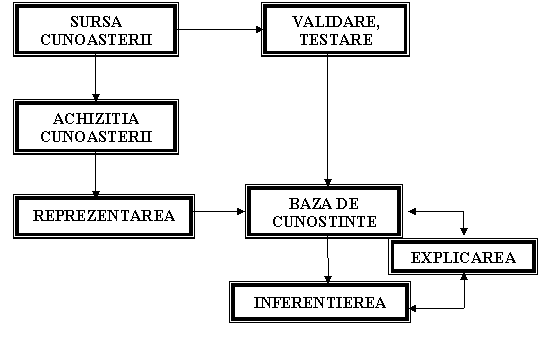
Figura 2.7 - Activitati de baza ale ingineriei cunoasterii

Cunoasterea poate fi achizitionata in mai multe moduri, insa voi prezenta doar trei dintre ele, cele mai generale si probabil cele mai intuitive.

Modelul de baza al achizitiei cunoasterii presupune o echipa de lucru, in care cogniticianul solicita prin metode specifice cunoasterea de la expert, o prelucreaza impreuna cu acesta si o reprezinta in baza de cunostinte.

Colectarea cunoasterii se realizeaza prin trei tipuri de metode: manuale, semiautomate, automate.

cerinte

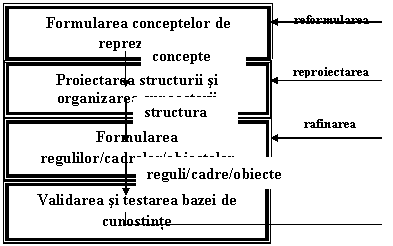
Figura 2.8 - Fazele achizitiei de cunostinte

Metodele manuale sunt lente, scumpe si uneori lipsite de acuratete. Schematic, acest tip de modele este reprezentat in figura 2.9.

Metodele semiautomate se impart in doua subcategorii :

Cele care ajuta expertii in construirea bazei de cunostinte, fara sprijinul cogniticienilor (figura 2.10). In cazul acesta se desfasoara si fazele de formalizare si implementare;

Cele care ajuta cogniticienii in executarea fazelor specifice achizitiei cunoasterii, eficient si rapid, uneori cu un mic ajutor din partea expertilor.

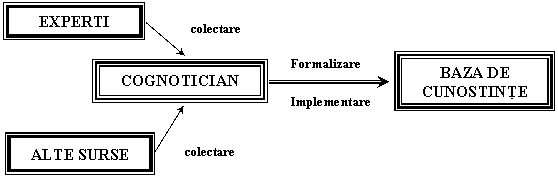
Figura 2.9 - Schema metodelor manuale de achizitie a cunoasterii

Figura 2.10 - Schema achizitiei semiautomate a cunoasterii

Rolurile cogniticianului si expertului sunt minimizate, daca nu chiar eliminate, in cazul metodelor automate de achizitie a cunoasterii. In cazul metodei inductiei, metoda ce face parte din acest tip de metode automate, achizitia cunoasterii o poate face chiar analistul proiectant, rolul cogniticianului fiind nul, iar al expertului, minim (figura 2.11).

Figura 2.11 - Schema achizitiei automate a cunoasterii prin metoda inductiei

Organizarea cunoasterii presupune luarea de decizii cu privire la metoda de reprezentare, verificarea cunoasterii si validarea lantului inferential. Aceste decizii se iau periodic in timpul achizitiei cunoasterii, cu scopul de a obtine o forma corespunzatoare pentru baza de cunostinte.

Verificarea este procesul de asigurare a corectitudinii bazei de cunostinte.

Validarea este la fel de importanta ca verificarea si se realizeaza cu scopul controlului acuratetei (claritatii si exactitatii) lanturilor inferentiale. Prin acest proces se observa daca sistemul expert realizat ofera rezultate (solutii) corecte.

Odata creata, baza de cunostinte nu trebuie considerata statica ci trebuie actualizata imediat ce apare o noua cunoastere.

Apar acum probleme noi cu privire la faptul ca baza de cunostinte va trebui sa foloseasca o combinatie intre cunoasterea deja existenta si cunoasterea nou achizitionata. De aceea trebuie sa se monitorizeze cu atentie procesul de adaugare de noi cunostinte si actualizarea bazei deja existente.

Este necesar ca baza de cunostinte sa fie intretinuta in permanenta, iar in cazul scaderii performantelor sistemului aceasta sa fie reproiectata.

Reprezentarea cunostintelor

Reprezentarea cunostintelor este metodologia de formalizare a cunostintelor in vederea memorarii acestora in baza de cunostinte.

Cunostintele din lumea reala pot fi grupate in doua categorii:

cunostinte precise;

cunostinte imperfecte.

Cunostintele precise pot fi reprezentate cu metodele furnizate de ingineria cunostintelor.

Pentru reprezentarea acestor cunostinte exista urmatoarele modele:

metoda regulilor de productie;

metoda frame-urilor (cadrelor);

metoda retelelor semantice;

metode logice: 

logica propozitiilor

logica predicatelor

Cunostintele imperfecte sunt acele cunostinte care prezinta anumite imperfectiuni si care nu pot fi reprezentate cu modelele furnizate de ingineria cunostintelor prezentate mai sus.

Pentru reprezentarea cunostintelor imperfecte pot fi folosite urmatoarele modele:

metoda coeficientilor de certitudine (pentru cunostinte incerte);

metode bazate pe logica probabilista (pentru cunostinte incerte);

metode bazate pe teoria si logica fuzzy (pentru cunostinte vagi);

metode bazate pe logica non-monotona (pentru cunostinte incomplete);

metode bazate pe teoria masurarii a lui Dempster si Schaffer (pentru cunostinte intuitive);

2.7.1 Reprezentarea cunostintelor precise

Modelul regulilor de productie

Cea mai folosita metoda de reprezentare a cunostintelor in sistemele expert este metoda regulilor de productie.

Conform acestei metode, o regula de productie are doua parti: partea de IF si partea de THEN, care stabilesc o relatie ce reprezinta scopul regulii.

Pentru descrierea relatiei IF-THEN (DACA-ATUNCI) s-au stabilit cateva perechi de termeni:

<antecedent><consecinta>

<conditie><actiune>

<premisa><concluzie>

Este folosit uneori simbolul implicatiei "→" in locul relatiei IF-THEN, in felul urmator:

<antecedent> → <consecinta>

Conform modelului cel mai general, o regula de productie se poate scrie cu sintaxa:

DACA (IF)

conditie1 AND

conditie2 AND

.

ATUNCI (THEN)

concluzie1 AND

concluzie2 AND

.

ALTFEL (ELSE)

concluzie'1 AND

concluzie'2 AND

.

unde:

conditie1, conditie2, .sunt antecedentele sau premisa;

concluzie1, concluzie2, .sunt actiunea sau consecinta;

AND reprezinta conectorul logic,
concluzie'1, concluzie'2, .sunt actiuni sau concluzii in situatia in care conditiile din partea de IF nu sunt adevarate.

In conformitate cu acest model, partea de THEN se va executa daca partea de IF este adevarata, iar partea de ELSE se executa in caz contrar. Conectorul logic poate fi prezent in toate cele trei parti ale unei reguli.

Vom prezenta cateva exemple de reguli de productie.

R1:  IF pacientul are temperatura

THEN este bolnav

R2:  IF persoana are salariu

THEN persoana este salariat

Actiunea/concluzia din regula se va executa numai daca este indeplinita (adevarata) premisa din IF. Regulile pot folosi si conectori logici. De exemplu:

R3: IF pacientul are temperatura AND

pacientul are dureri de cap

THEN pacientul este racit

Reprezentarea exacta a cunoasterii dintr-un domeniu particular necesita un numar mare de reguli, ca sa poata fi surprinse toata detaliile. Numarul regulilor este direct proportional cu complexitatea cunoasterii (expertizei).

Regulile sunt in mod uzual intercorelate in sensul ca actiunea sau concluzia dintr-o regula se pot gasi in premisa sau antecedentele altei reguli. In acest caz, actiunea finala va implica o inlantuire a regulilor in liniile de rationament. De exemplu:

R5:  IF (clientul are un cont)

AND (contul nu a fost utilizat 90 de zile)

THEN (marcheaza contul cu "inactiv")

R6:  IF (contul este "inactiv")

THEN (anunta clientul pentru a restabili relatia de afaceri)

R7:  IF (clientul nu mai doreste afaceri)

THEN (sterge clientul din baza de date)

In acest exemplu, regulile R5, R6 si R7 sunt intercorelate in sensul ca R6 este invocata doar daca R5 este adevarata, iar R7 se invoca numai daca R6 este adevarata. Toate aceste reguli stabilesc un lant de actiuni, care poate fi parcurs intr-un sens sau altul, inainte sau inapoi, pentru controlul inferentelor.

Reprezentarea cunoasterii sub forma de reguli a devenit cel mai extins model. Divizarea cunoasterii in fragmente sau piese de cunoastere face ca baza de cunostinte sa fie organizata modular astfel incat sa poata fi usor modificata.

Modelul Frame-urilor (cadrelor)

Aceasta metoda este mai complicata decat cea cu reguli, pe care am prezentat-o pana acum. Sloturile ofera un mecanism de rationament numit prelucrare orientata pe asteptari (expectation-driven processing). Sloturile goale se pot umple, in anumite conditii, cu date (cunostinte) care confirma asteptarile. In acest fel, rationamentul urmareste daca se confirma asteptarile, moment in care sloturile se vor umple cu valori. In absenta altor informatii, valoarea implicita atasata unui slot se pastreaza in continuare.

Se pot face inferente despre noi obiecte, evenimente si situatii, deoarece cadrele ofera o baza de cunostinte stabilita pe experienta anterioara.

Acest rationament se poate realiza, fie cu reguli, fie in mod ierarhic.

O regula poate infera despre caracteristicile unui cadru prin referire la valoarea sloturilor sale. De exemplu, o ruta de transport catre o destinatie, spre care un pod defect trebuie ocolit de vehiculele de mare tonaj. Baza de cunostinte va contine in acest caz o regula de tipul:

R1:  IF ?MASINA este-un AUTOMOBIL

AND ?MASINA are-un ?MOTOR

AND ?MOTOR este-un DIESEL

THEN Stabileste CARBURANT

al ?MASINA pentru CAMIOANE

In cazul acesta, pe prima linie din IF Motorul inferential asteapta instantierea variabilei ?MASINA, cu fiecare cadru, dar se vor retine numai situatiile care sunt membre ale clasei AUTOMOBIL. Pe a doua linie se instantiaza variabila ?MOTOR, cu fiecare cadru de tipul ?MASINA pentru a observa vreo relatie. Pe linia a treia se trece prin orice instantiere a regulii pentru care ?MOTOR nu este membru al clasei DIESEL. Pe linia a patra se stabileste, in final, slotul CARBURANT vehiculului asociat la valoarea CAMIOANE.

In rationamentul ierarhic, anumite alternative sau evenimente sunt eliminate de la diferitele niveluri ale ierarhiei cautarii. De exemplu, la un nivel trebuie urmatoarea regula:

R2: IF FABRICA de ?MASINA este DACIA S.A.

THEN ?MASINA nu-este MEMBRU de DIESEL

Aceasta regula va elimina un numar de clase si subclase de la operatia de instantiere.

O alta metoda de studiu a cunoasterii imprecise este cea bazata pe teorema lui Bayes, dar aceasta va face subiectul celui de-al treilea capitol al prezentei lucrari.

Modelul retelelor semantice

Reteaua semantica este o modalitate grafica de reprezentare a cunoasterii, si anume un graf orientat in care cunoasterea este prezenta in asocierea la noduri si arce a semnificatiei sau semanticilor. Se ajunge astfel la interpretarea in termeni de obiecte (entitati) si relatii a domeniului problemei.

In formalizarea cunoasterii printr-o retea semantica, cea mai frecventa interpretare este urmatoarea: nodurile sunt asociate obiectelor (concepte, evenimente,.) din domeniu, iar arcele sunt asociate legaturilor sau relatiilor dintre obiecte. Astfel, doua elemente din domeniul problemei sunt in legatura directa daca doua noduri care le corespund intr-un graf sunt conectate printr-un arc.

In mod obisnuit se practica o anumita modalitate de etichetare a nodurilor si arcelor astfel incat diferitele tipuri de obiecte din domeniu si relatiile dintre ele pot coexista in acelasi graf fara ambiguitati.

Caracteristica de baza a unei retele semantice consta in aceea ca ofera un formalism de reprezentare a cunoasterii impreuna cu o structura de regasire a cunoasterii. Obiectele care au legaturi cu un obiect dat pot fi gasite prin urmarirea legaturilor care pleaca de la nodul asociat lui in retea. In acest mod se poate formaliza si conceptul de rationament. In reprezentarea prin retele semantice rationamentul inseamna cautarea unei cai dintre nodurile grafului folosind cunoasterea disponibila din domeniu.

Algoritmii de cautare a cailor dintr-un graf se pot utiliza ca baza pentru implementarea unui program de navigare prin retea.

Retelele semantice pot fi utilizate la achizitia cunoasterii generale si a cauzalitatii. In acest fel pot exista retele de cauzalitate si grafuri de dependenta, foarte utile pentru formalizarea cunoasterii in sistemele expert de gestiune.

In retelele de cauzalitate, semnificatiile asociate nodurilor si arcelor pot sa difere in functie de problema de solutionat. Nu exista o modalitate standard de utilizare a retelelor semantice.

Voi prezenta in continuare un exemplu de retea semantica de tip cauzal pentru macroeconomie, definit dupa cum urmeaza:

Un set de stari in care fiecare stare se caracterizeaza printr-un set de atribute sau variabile, fiecare cu valoarea lor;

Un set de restrictii (logice, matematice, axiome si reguli de inferenta) ca relatii dintre aceste stari;

In modelul economic pe care ne-am propus a-l exemplifica, nodurile reprezinta stari, iar arcele reprezinta restrictii. Starile sunt:

Consumul intern (CI);

Salariul indexat (SI);

Comenzile;

Profitul sectorului public si privat (PSPP);

Importul (I);

Utilizarea capacitatilor de productie (UCP);

Exportul (E);

Balanta comerciala (B);

Nivelul stocurilor (NS).

Legaturile sunt reprezentate prin arce cu sageti care indica relatia de cauzalitate.(figura 2.12)

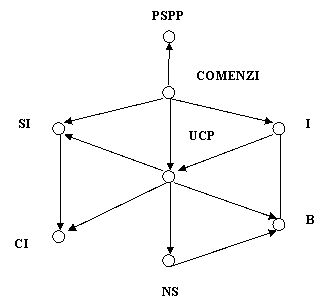
Figura 2.12 - Retea semantica de tip cauzal

Retelele semantice de tip cauzal reprezinta cauzalitatea in mod explicit, iar justificarile privind influenta unei stari asupra alteia se pot construi pe baza legaturilor dintre doua stari. Prin utilizarea legaturilor cauzale sunt mai usor de rezolvat problemele de gestiune, iar prin abstractizari matematice se pot explica rezultatele.

Greutatea explicarii semnificatiei solutiilor in termenii influentei reciproce a cauzalitatilor a determinat folosirea retelelor cauzale in locul relatiilor matematice. Retelele semantice capteaza cel mai bine distinctia dintre cauza si efect. Legatura dintre obiecte se poate interpreta ca o legatura de tipul: "are o influenta directa asupra". Cea mai importanta este directia legaturii dintre doua obiecte. De exemplu, cunoasterea ca "I are o influenta directa asupra lui B" difera de cunoasterea ca "NS are o influenta asupra lui B", conform figurii 2.12 de mai sus.

Directia legaturii se defineste cu ajutorul sagetii de la nodul cauza la nodul efect, fiind foarte importanta in astfel de retele.

Avantajele acestor retele sunt:

Adecvarea foarte buna la achizitia cunoasterii cauzale incomplete;

Imbunatatirea intelegerii si explicatiilor pe care trebuie sa le ofere sistemul expert.

In afara de aceste retele semantice de cauzalitate mai exista si retele care se reprezinta cu ajutorul grafurilor de dependenta si o metoda care s-a utilizat in cazul sistemului MYCIN, asa numita metoda OAV (Obiect-Atribut-Valoare). Aceste metode nu fac insa obiectul acestei lucrari, prin prezentarea detaliilor de mai sus dorindu-se doar conturarea, in linii mari, a retelelor semantice.

Modele logice

Pentru atingerea scopului urmarit de un sistem expert este necesar formalizarea conceptului de rationament.

In acest proces, asocierile conectate la conceptele individuale nu au nici un rol si numai cunoasterea relevanta este cea care trebuie explicit reprezentata. Inferentele se executa numai in conformitate cu reguli explicite.

Atat calculul predicatelor, cat si calculul propozitional se bazeaza pe logica matematica. Metodele logice sunt adecvate pentru reprezentarea cunoasterii in majoritatea ipostazelor specifice aplicatiilor de gestiune. Calculul predicatelor este uneori utilizat in sistemele expert, fiind preferat datorita structurilor sale si puterii de inferentiere. El sta la baza PROLOG-ului, cel mai utilizat limbaj de programare logica, fara a fi mai usor de implementat fata de metodele bazate pe reguli, cadre sau retele semantice.

CALCULUL PROPOZITIONAL

Calculul propozitional este o logica simbolica pentru manipularea propozitiilor si este in legatura cu variabilele logice numite propozitii. In general, enunturile, frazele sunt de patru tipuri : imperative; interogative; exclamative; declarative.

Calculul propozitional are in vedere enunturile declarative, repartizate in doua grupe: false si adevarate. Enuntul a carei valoare de adevar poate fi determinata se numeste propozitie. O propozitie compusa este formata din propozitii elementare legate cu ajutorul conectorilor logici : (AND), (OR), ~(NOT) si (implicatia), (echivalenta).

O propozitie este un enunt care poate avea o valoare de adevar (True sau False) si se mai numeste, in acest caz, asertiune.

Din start se presupune ca poate fi o premisa care poate fi utilizata in derivarea(inferarea) unor noi propozitii. In acest caz, se utilizeaza reguli in procesele inferentiale de acest gen, in care se determina valoarea de adevar a noilor propozitii derivate.

Calculul propozitional este adecvat pentru unele probleme, dar sufera pentru ca propozitiile nu pot fi fragmentate in parti, ci trebuie tratate ca un intreg. Acest lucru nu satisface cele mai multe situatii din realitate in care intervin detalii.

CALCULUL PREDICATELOR

Calculul predicatelor permite ca o propozitie sa fie fragmentata in doua parti de baza: obiecte (argumente); predicate (asertiuni despre atributele obiectelor).

Calculul predicatelor permite totodata utilizarea variabilelor si functiilor de variabile, face uz de enunturile logicii simbolice si permite utilizarea tuturor proprietatilor calculului propozitional.

Puterea variabilelor consta in generalizare, in sensul ca propozitia care poate fi nuantata in termeni generali este mai utila decat propozitia despre o situatie particulara.

Calculul predicatelor utilizeaza si cuantificatori. Un cuantificator se reprezinta printr-un simbol care stabileste domeniul unei variabile (limitele). Este vorba despre cei doi cuantificatori utilizati mai inainte :

cuantificatorul universal, care stabileste ca o propozitie care contine o variabila este "true" pentru toate valorile posibile ale variabilei.

cuantificatorul existential, care stabileste ca o propozitie este "true" pentru cel putin o valoare a variabilei.

Logica are o importanta deosebita in sistemele expert, in care motoarele de inferenta actioneaza de la premise catre concluzii. Un termen semnificativ pentru programarea logica si sistemele expert este acela de sisteme de rationament automat (Automated Reasoning Systems).

Reprezentarea cunostintelor imperfecte

Reprezentarea cunostintelor incerte

Incertitudinea, intr-o mare masura, este o parte a mecanismelor inferentiale, mai ales cand se utilizeaza deductia sau abductia.

In cazul deductiei este de cele mai multe ori imposibil de stiut toate faptele necesare pentru inferarea unei concluzii. In acest caz trebuie sa se hotarasca de la ce punct va incepe deductia, in ciuda lipsei tuturor premiselor necesare.

Aceleasi situatii pot fi intalnite si la utilizarea rationamentelor inductive. Din acest motiv, sistemele expert trebuie sa rationeze cu o cunoastere incompleta, incerta sau imprecisa.

Sistemele pot cere utilizatorului sa introduca si apoi sa primeasca o informatie daca poate sau nu sa raspunda la o intrebare. Sistemele expert trebuie sa tina cont de lipsa cunoasterii atunci cand fac rationamente deoarece vor ajunge la o concluzie sau raspuns care de cele mai multe ori difera de cel anticipat.

Incertitudinea poate fi tratata ca un proces care se desfasoara in trei etape (figura 2.13).

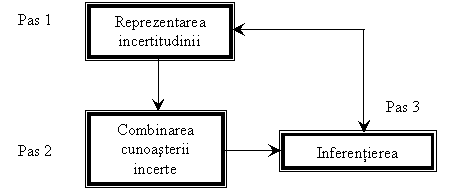
Figura 2.13 - Inferentierea cu cunostinte incerte

La pasul 1 - prima etapa, expertul ofera cunoasterea imprecisa, incerta, care este in termeni euristici (reguli) cu valori de probabilitate.

La pasul 2, cunoasterea imprecisa se foloseste direct la producerea inferentelor. In multe situatii, evenimentele, situatiile, conceptele reprezentate sunt necorelate si devine necesara combinarea cunoasterii oferita in prima etapa. In acest scop se pot folosi cateva metode mai cunoscute: metoda Bayes, teoria evidentei, teoria factorilor de certitudine sau teoria seturilor fuzzy.

In etapa a treia, scopul sistemului expert este producerea de inferente.

Factorii de certitudine

Incertitudinea este studiata cu ajutorul factorilor de certitudine - confidence factors (engleza). Ei masoara gradul de incredere (confidenta) al cunoasterii implicate in sistemele expert. Ei nu trebuie confundati cu coeficientii de probabilitate deoarece factorii de certitudine reflecta increderea in cunostinte (fapte, reguli) mai degraba decat probabilitatea.

De exemplu, daca spunem "sansa de a fi inflatie este de 50%", nu inseamna ca probabilitatea este de 0.5 ca acest fapt sa se implineasca. Inseamna ca specialistul in previziuni are incredere in proportie de 50% in faptul respectiv, proportie la care a ajuns in urma unor calcule, cu numerosi factori generatori de inflatie, facute in prealabil, uneori chiar calcule statistice. Dupa cum se stie, statistica nu este o stiinta a exactitatii.

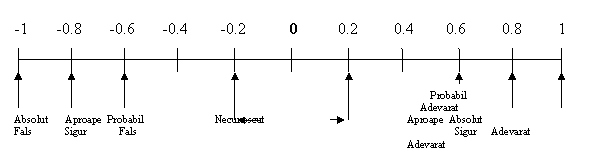
Conventie: Vom considera in exemplul nostru drept factori de certitudine numerele cuprinse in intervalul -1(pentru incertitudine sau neincredere absoluta) si +1 (pentru certitudine sau incredere absoluta).(figura 2.14)

Figura 2.14 - Factor de certitudine utilizat in sistemul MYCIN

Factorul de certitudine reprezinta o metoda conventionala utilizata in sistemele expert pentru gestionarea cunoasterii incerte. El este o valoare unica atasata unei premise sau unei concluzii dintr-o regula si reprezinta gradul de incredere in acel enunt.

Factorii de certitudine sunt de multe ori atribuiti de catre experti in baza rationamentelor lor specifice. Ei se pot schimba in timpul proceselor inferentiale si astfel o noua cunoastere se adauga, dar in orice moment ei au valori statice. Factorii de certitudine se pot asocia atat premiselor (IF), cat si concluziilor (THEN) din reguli.

Exemplu :

IF A (FC=0.6)

THEN B

IF C

THEN D (FC=0.8)

Aceste doua reguli stabilesc un nivel, un prag, adica o valoare de care este nevoie pentru factorul de confidenta astfel incat o regula sa se declanseze in executie. Acest prag este stabilit de catre cognotician in urma consultarii cu expertul. Acest prag poate diferi de la o regula la alta.

Pentru a face o exemplificare este nevoie sa luam in seama efectul valorilor pragului atunci cand mai multe reguli sunt inlantuite la executie.

In practica se foloseste tehnica mediei fara sa se fi stabilit un consens asupra celei mai bune tehnici pentru determinarea valorii pragului. Validitatea pragului trebuie intotdeauna testata in timpul rafinarii (utilizarii) sistemelor expert.

Exista, in sistemele expert, reguli cu mai multe conditii in premise. Agregarea factorilor de certitudine atasati fiecarei conditii nu este standardizata in randul cognoticienilor, desi propagarea lor a facut obiectul mai multor cercetari.

Exemplu :

IF A (FC=0.6)

AND B (FC=0.3)

AND C (FC=0.8)

THEN D

Intrebarea fireasca este ce factor de certitudine sa i se atribuie lui D? Raspunsurile difera de la cognotician la cognotician:

Unii argumenteaza ca trebuie folosit cel mai mare dintre factorii atasati conditiilor;

Altii motiveaza ca cel mai bun este factorul cel mai mic;

Altii sunt de parere ca o medie a factorilor atasati conditiilor ar fi cel mai indicat.

O problema asemanatoare se intalneste in cazul executiei unui lant de reguli. Nici aici nu sunt propuneri general acceptate si daca o regula a fost elaborata incorect atunci incorectitudinea se va propaga in tot lantul inferential.

Desi lucrul cu incertitudinea este un avantaj recunoscut al sistemelor expert, aceasta poate deveni foarte usor un dezavantaj dezastruos daca nu este corect tratata de catre cognotician si expert. Ei trebuie sa studieze toate alternativele posibile pentru a mentine credibilitatea sistemelor expert.

Reprezentarea cunostintelor imprecise (vagi)

Pentru reprezentarea cunostintelor imprecise sau vagi se foloseste teoria si logica fuzzy.

Logica fuzzy este una dintre cele mai interesante metode de tratare a incertitudinii. Aceasta tehnica reprezinta o cale de a lucra cu valori neambigue in contextul cunoasterii ambigue (imprecise).

Se poate spune ca "inflatia este mare", insa "mare" este un termen vag, neprecizand cat de mare este referinta: 2%, 15%, 100% sau 200%. O valoare particulara a valorii inflatiei trebuie data in mod obligatoriu. Logica fuzzy isi propune sa defineasca asemenea termeni imprecisi, cum sunt: "inalt", "mare", "mic", "rapid", "tare", etc. Prin logica fuzzy se poate defini un asemenea termen prin asocierea unei limite cu ajutorul unui coeficient de probabilitate. In acest fel, termenii asemanatori celor de mai sus devin cuantificabili cu valori exacte, nemaifiind ambigui. (figura 2.15).

Termenii imprecisi (ambigui) sunt reprezentati prin seturi fuzzy, care capteaza din punct de vedere cantitativ interpretarea calitativa a termenilor. Figura 2.15 indica trei seturi fuzzy pentru domeniul marimii inflatiei printr-un numar numit valoare membru sau grad de apartenenta. Aceasta valoare este un numar din intervalul [0,1], care reflecta nivelul de incredere al expertului ca o marime data a inflatiei corespunde unui set fuzzy dat. De exemplu, o inflatie de 35% va fi una medie care corespunde valorii membru 1. In plus, logica fuzzy, permite scrierea regulilor fuzzy, care contin seturi fuzzy atat in parte de IF, cat si in parte de THEN.

Exemplu :

IF Inflatia este mare

THEN Rata dobanzii este mare.

Reprezentarea termenilor imprecisi este de mare complexitate si dificultate. Din acest motiv logica fuzzy nu este inca utilizata pe scara larga in sistemele expert.

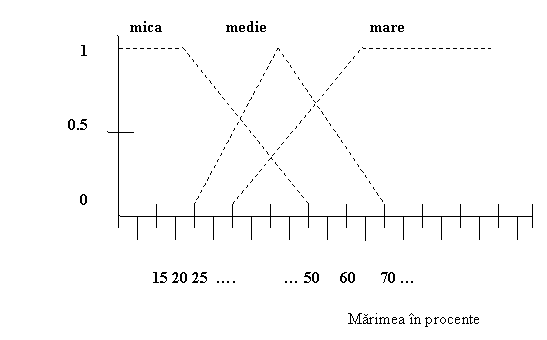
Figura 2.15 - Seturi fuzzy pe marimea inflatiei

2.8. Modele de dependenta

Un model de dependenta este capabil de a modela relatiile de dependenta intre simptome.

2.8.1. Modelul general de dependenta

Daca motorul inferential are nevoie de probabilitatile , expresia (3) arata ca un model general, ar trebui sa aiba ca parametri (tabelul 3.1) toate frecventele si . Acest model care contine numarul maxim de parametri se numeste "modelul general de dependenta".

Problema principala cu acest model este aceea a numarului extrem de mare de parametri. Acest numar pentru n boli si m simptome (binare) este (n+1)2^m.

Modelul de dependenta al simptomelor relevante

Numarul de parametri ai modelului poate fi enorm redus selectand, pentru fiecare boala E_i, setul simptomelor relevante asociate Q_i = si presupunand ca restul simptomelor sunt independente intre ele si independente de simptomele relevante (Castilo si Alvarez (1987,88), Castilo si altii (1988)). Rezulta de aici ca frecventele pot fi calculate cu ajutorul formulei:

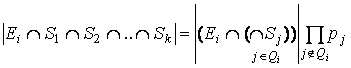
unde Q_i este setul simptomelor relevante pentru boala E_i si p_j este probabilitatea simptomei nerelevante cu numarul j. De observat, inca o data, presupunerea independentei simptomelor nerelevante. Acest model se numeste "modelul de dependenta al simptomelor relevante".

Cu aceasta presupunere numarul parametrilor nu este mai mare de n2^r+1+m, unde r este numarul maxim de simptome relevante pentru o singura boala.

Tabelul 3.1 rezuma numarul parametrilor asociati modelelor discutate si arata cum ei pot fi reactualizati cand bolile si simptomele unui nou pacient devin cunoscute.

Tabelul 2.16 - Parametrii si actualizarea modelelor de dependenta

2.9. Modele de Independenta

Cele mai comune modele sunt modelele de independenta. Acest nume se datoreaza faptului ca ele presupun independenta statistica a simptomelor pentru o boala data. Dintre toate aceste modele, cel mai des folosit este "modelul general de independenta", care este descris mai jos.

Presupunerea independentei permite expresiei (3) sa fie scrisa astfel:

=

= =

=

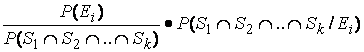
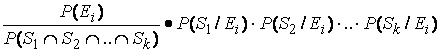ceea ce arata cum cunoasterea unei noi simptome modifica probabilitatile tuturor bolilor. Initial, probabilitatile sunt P(E_i) si mai tarziu devin proportionale cu P(S_j / E_i), pentru j=1, 2, .. ,n. Fiecare noua simptoma conduce la un nou factor si la o schimbare in factorul normalizator .

Ca parametri ai acestui model putem alege frecventele |E_i|, (i=1, 2, .. , n), |S_j |, (j= 1, 2, .. , m) , si N (Tabelul 3.2). Actualizarea parametrilor, cand noi pacienti sunt adaugati in baza de date, implica cresterea cardinalilor (numarului de elemente) seturilor corespunzatoare cu o unitate (Tabelul 3.2).

Cu aceasta presupunere a independentei simptomelor, numarul parametrilor este redus considerabil. Daca avem n boli si m simptome numarul de parametri devine nm+m+n+1 in loc sa fie (n+1)2^m ca in cazul general. Oricum, acest numar este prea mare (pentru n=90 si m=143 avem parametri). Acesta este motivul pentru care metoda nu a fost utilizata la scara mare in practica.

O posibila solutie la aceasta problema este presupunerea probabilitatilor P(S_j / E_i) pentru anumite seturi de simptome nule sau, mai precis, pentru fiecare boala E_i sunt alese cateva simptome relevante S₁, S₂, .. , S_m (relativ putine), iar probabilitatile P(S_j / E_i) sunt facute nule daca S_j nu este simptoma relevanta. In acest fel, numarul parametrilor nu este mai mare decat nr+n+m+1 unde r<<m (r este mult mai mic decat m) este numarul maxim de simptome relevante pentru fiecare boala (in cazul nostru, daca r= avem p= , care este mai mica decat valoarea anterioara de ).

Aceasta solutie are cateva dezavantaje, deoarece daca o simptoma non-relevanta este prezenta la un pacient, boala este exclusa (probabilitatea asociata bolii este facuta zero). Din punct de vedere practic aceasta concluzie este inadmisibila pentru ca este foarte posibil ca pacientii sa prezinte unele simptome care nu au nimic in comun cu boala de care sufera.

Pentru a rezolva aceasta problema se poate presupune ca P(S_j/E_i)=p_j≠0 pentru toate simptomele nerelevante. Acest lucru implica adaugarea a doar inca m parametri modelului. Este o crestere foarte mica (in exemplul dat avem in loc de , parametri).

Reactualizarea parametrilor cand este adaugat un nou pacient in baza de date este ilustrata in Tabelul 3.2. Se observa ca nu este posibila actualizarea lui p_j.

Modelul de independenta nu este realistic in multe situatii, datorita prezentei anumitor sindroame (grupuri de simptome). Pentru astfel de cazuri, un model de dependenta este mult mai potrivit.

Tabelul 2.17 - Parametrii si actualizarea modelelor de independenta