Parcurgerea grafurilor neorientate
Prin parcurgerea unui graf se întelege "vizitarea" vârfurilor sale într-o anumita ordine, data de un anumit criteriu.
Exista doi algoritmi de parcurgere a grafurilor neorientate:
algoritmul de parcurgere în latime BF;
algoritmul de parcurgere în adîncime DF.
Algoritmul de parcurgere în latime BF
Se porneste de la un vârf de start care se viziteaza, apoi se viziteaza toti vecinii lui. Pentru fiecare dintre aceste vârfuri, se viziteaza vecinii lui care nu au fost înca vizitati. Pentru noile vârfuri se procedeaza la fel: se viziteaza vecinii acestora care nu au fost înca vizitati. Procedeul continua pâna când s-au vizitat toate vârfurile.
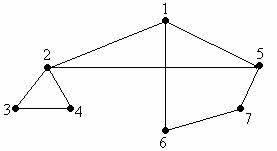
Figura 9.
Exemplu:
Fie graful G=(X,U) din figura 9. presupunem ca vârful de start este 1.
|
Pasii parcurgerii |
Noduri vizitate |
|
Vizitam mai întâi vârful de start unu; | |
|
Vizitam apoi vecinii lui 1, care sunt 2, 5 si 6 | |
|
Pentru fiecare dintre acesti vecini ai lui 1, vizitam si vecinii sai nevizitati înca: vecinii lui 2 sunt 1, 3 si 4, dar nevizitati sunt decât 3 si 4 vecinii lui 5 sunt 1, 2 si 7, dar nevizitat este numai 7 vârful 6 nu mai are vecini nevizitati | |
|
Am vizitat pâna acum vecinii vârfurilor 1,2,5 si 6. Mai trebuie vizitati vecinii noilor vârfuri vizitate la pasul anterior, si anume vecinii vârfurilor 3,4 si 7. Dar observam ca vârfurile 3,4 si 7 nu mai au vecini nevizitati.deci parcurgerea se încheie. |
Ordinea vizitarii în parcurgerea BF este 1, 2, 5, 6, 3, 4, 7.
2. Algoritmul de parcurgere în adâncime DF
Metoda este urmatoarea: alegem vârful de pornire, pentru acesta se alege primul vecin al sau nevizitat înca, pentru acest vecin cautam primul vecin al sau nevizitat si asa în continuare. În cazul în care un vârf nu mai are vecini nevizitati atunci ne întoarcem la nodul anterior, iar pentru acel nod cautam urmatorul vecin nevizitat al sau.
Pentru graful de mai sus parcurgerea în adâncime plecând de la vârful 1 este: 1,2,3,4,6,7,5.
|