Patrate magice impare

Patrate magice impare

Se considera numarul natural impar n≥3 si ansamblul crescator de numere reale distincte

A = [a₁<a₂<.<a_n² ]

ale carui elemente sunt in progresie aritmetica de ratie r >0.

Sa se proiecteze un algoritm cu A astfel incat elementele ansamblului precizat sa genereze cel putin o matrice patratica.

A=(a_ij)_n*n

care sa verifice simultan egalitatile:

= S_n

Unde S_n are o valoare care se va preciza.

Descriere algoritmului:

Determinam S_n - suma magica de ordinal n asociata ansamblului A.

(a₁+a _n²)n² (a₁+a_n²)n

∑ A=  =nS_n S_n=

2 2

Daca [n] = multimea primelor n numere naturale,

Se defineste functia

f : A → [n²] ; f(a_i)=i, oricare ar fi a_i A

Deoarece n este impar generarea unui patrat magic se face cu ajutorul metodei teraselor (BACHE):

Se considera un caroiaj patratic de dimensiuni (2n-1)(2n-1) de tipul:

n......2n-1

a_n²
a_n²_-n+1

In caroiajul considerat se considera ca origine mijlocul oricarei laturi frontiere a caroiajulu; deci caroiajul poate avea patru puncte origine.

Pentru a face o alegere vom presupune ca mijlocul laturii frontiera cea mai din stanga este originea aleasa. Acum trebuie precizat si un sens de terasare a elementelor ansamblului . Sensul de terasare este sensul de la originea aleasa la mijlocul uneia din laturile frontiera cea mai apropiata.

Deci dintr-o origine pot fi considerate doua sensuri de terasare.

Odata sensul de terasare precizat, terasarea elementelor ansamblului se va face in ordinea crescatoare a valorii lor , in terase paralele si egale ca numar de elemente, pana la epuizarea elementelor.

Se vor obtine n terase, fiecare avand n elemente.

In urma terasarii s-a obtinut un romb valoric de tipul:

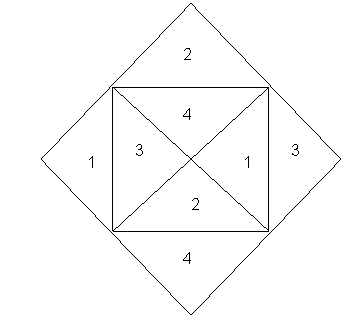
Unind mijlocul laturilor rombului si ducand diagonalele patratului interior s-au obtinut patru triunghiuri valorice exterioare patratului si patru triunghiuri valorice interioare patratului.

Oricare doua triunghiuri valorice, unul interior si unul exterior sunt complementare

in sensul ca :daca, intr-un triunghi valoric, o anumita pozitie a sa este ocupata de un element al ansamblului, atunci in celalalt triunghi considerat, pozitia corespunzatoare este libera. Aceasta inseamna ca, daca se suprapune un triunghi valoric exterior peste oricare din triunghiurile valorice interioare se va obtine un triunghi valoric plin, adica un triunghi in care toate pozitiile lui sunt ocupate de elemente ale ansamblului A.

Suprapunand triunghiurile valorice exterioare peste cele interioare se va obtine o matrice patratica plina.

Matricea valorica plina obtinuta prin suprapunerile indicate anterior reprezinta un patrat magic de ordinal n asociat ansamblului precizat.

Deoarece in caroiajul precizat pot fi considerate patru origini, iar din fiecare origine pot fi considerate doua sensuri de terasare ,pot fi generate opt matrici distincte pentru acelasi ansamblu si aceeasi suma magica S_n.

Cazuri particulare

Sa se exemplifice aplicatia pentru fiecare din urmatoarele cazuri:

a) A= ; n=5

b) A =; n=5

a)  A =

= = 65.

n=5, n²=25, Matricea va fi de dimensiunea 9 X 9 ( 2 5-1=9)

Avem 8 matrici distincte care se pot forma in acest fel. A₁ = .

b) A = card A = 25. Se defineste functia f :A → ; f(a_i) = i. Functia este bijectiva, pastraza valoarea si ordinul de marime ale elementelor, deci putem descrie generarea unui patrat magic pe o multime de numere naturale consecutive : A' = ; problema se reduce la exemplul anterior. S_n=125.

A₁=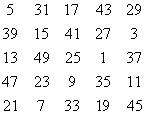

Patrate magice pare

Se considera un ansamblu crescator de numere reale distincte,

A = ; cu n-par, in care elementele apartin unei progresii aritmetice de ratie r > 0.

Cu elementele ansamblului A se genereaza o matrice patratica B utilizand relatia de ordine direct lexicografica (linie-linie) sau invers lexicografica (coloana-coloana). Presupunem ca B este generata direct lexicografic.

Pe multimea permutarilor S_n consideram P = (p₁, p₂, , p_n) = .

Calculam S = .In ordinea direct lexicografica

S_n = n ) = n (p₁+ p₂+ +p_n) - n² + =

= (n+1) - n² = =   - n² = .

Pentru a genera din matricea B, patratul magic A se considera din multimea grupului de permutari S_n, n permutari p¹, p², ,pⁿ paralele cu diagonala principala a matrici B.

p¹ = (1, 2, , n). Elementele precizate de permutarea respectiva vor fi considerate linii sau coloane in patratul magic ce urmeaza a fi generat.

Exemplu 1.

A = . B = . S₄ =

p = (2, 3, 1, 4)   S_p = b₂₃+b₃₁+b₁₄+b₄₂ = 7+9+4+14=34

p¹=(1, 6, 11, 16) ; p²=(2, 7, 12, 13) ; p³=(3, 8, 9, 14) ; p⁴ = (4, 5, 10, 15)   S_p=34.

Cosideram doua caroiaje a cate 16 casute fiecare si trasam diagonalele.

In casutele primului patrat vom trece in ordine crescatoare numerele date, omitand pentru moment pe cele care ar trebui scrise in casutele barate de diagonale. Numerele omise, incepand cu cel mai mare din ele (adica 16), le dispunem succesiv, in ordine descrescatoare, incepand din coltul din stanga de sus, in casutele barate de diagonale ale patratului al doilea. Suprapunand cele doua patrate asa fel incat casutele sa coincida exact, obtinem patratul magic cautat de categoria a patra.

Exemplu 2.

A = . S₆ =

Consideram un caroiaj de 36 de casute si il impartim in 4 patrate de cate 9 casute. Numerele de la 1 la 9 le vom aseza in patratul din stanga sus, dupa principiul alcatuirii unui patrat de categorie impara. Dupa acelasi principiu vom completa cu numere si celelalte 3 patrate de cate 9 casute: cel din dreapta jos - cu numere de la 10 la 18, cel din dreapta sus - cu numere de la 19 la 27 si, in sfarsit, cel din stanga jos cu numere de la 28 la 36.

Dupa aceasta e necesar ca numerele 4, 5 si 8 sa schimbe locurile cu numerele 31, 32, 35 - si patratul magic este gata.