Academia de studii Economice Bucuresti, Facultatea Cibernetica, Statistica si Informatica economica
Proiect la Teoria Jocurilor
Elementele de baza si presupuneri in teoria jocurilor
Utilitatea
Un agent este prin definitie o entitate cu preferinte. Teoreticienii jocului ca si economistii si filozofii ce studiaza modul in care se iau decizii rationale, descriu aceasta ca pe un concept numit uitilitate. Asta se refera la satisfactia ce o obtine un agent de la un obiect sau de la un eveniment. Prin satisfactie se intelege la anumite indexari normative la o situatie de un bine acceptabil ce se justifica printr-un bagaj al cunostintelor capatate in timpul muncii. De exemplu, am putea evalua bunastarea relativa a unor tari (pe care noi le putem drept agenti pentu anumite scopuri) luand ca punct de referinta castigul pe cap de locuitor, si am putea evalua bunastarea relative a unui animal in contextual predictiunii si explicatiilor dispozitiilor comportamentale ale acestuia. In cazul oamenilor, este cel mai tipic in economie si aplicatii in teoria jocurilor sa se evalueze bunastarea relativa a lor referindu-ne la parerea lor implicita sau explicita. Astfel o persoana care spune ca adora gustul de rodie dar uraste gustul cepei ar fi trist sa asociem utilitatea crescuta cu state ale lumii in care, toti ceilalti fiind egali, ea ar consuma mai multe rodii si mai putina ceapa decat statele in care se consuma mai multa ceapa decat rodii. Exemple de acest tip de sugestii in care utilitatea denota o parte din satisfacerea psihologica subiectiva, si asta este intr-adevar modul in care acest concept a fost interpretat in general inaintea anilor 1930.
In timpul acelui deceniu economistii si psihologii sub influ 949c26j enta comportamentului orientat catre folosirea teoretica ale unor asemenea entitati ca "satisfacerea psihologica". Economistul Paul Samuelson (1938) a definit utilitatea intr-un mod incat aceasta devine un concept pur tehnic. Astfel cand spunem ca un agent actioneaza in asa fel incat sa isi maximizeze utilitatea, noi intelegem prin utilitate pur si simplu ceea ce provoaca unui agent un comportament care sa sugereze satisfactia. Daca acest lucru pare circular sa stiti ca asa si trebuie: teoreticienii care il urmeaza pe Samuelson intentioneaza sa actioneze in sensul cresterii utilitatii ca pe o tautologie.
Astfel am putea sa nu mai miscati de scrupule ce deriva din comportamentul psihologic, multi teoreticieni continua sa il urmeze pe Samuelson in modul de a intelege utilitatea prin gandire. Este important ca acest joc al teoriei sa se aplice oricarui tip de agent - o persoana, o bere, o albina, o firma sau o tara - si nu doar agentilor cu constiinta de sine. Cand asemenea teoreticieni spun ca agentii actioneaza in scopul maximizarii utilitatii, ei vor ca aceasta sa fie o parte a definitiei a ceea ce inseamna sa fii agent, nu doar presupuneri despre propriile motivatii. Conceptia lui Samuelson despre utilitate definite in "Teoria revelarii preferintelor" introdusa in clasica lucrare (Samuelson 1938) ce satisface aceasta cerere.
Alti cativa teoreticieni inteleg problema teoriei jocului intr-un mod diferit. Ei privesc problema teoriei jocului ca pe una care aprovizioneaza un cont exploratory de strategii motivatoare. Pentru ca aceasta idée sa fie aplicabila trebuie sa presupunem ca agentii cel putin cateodata fac ceea ce fac in setari non-parametrice pentru ca logica teoriei jocurilor recomanda actiuni la fel de certe ca si cele rationale. Totusi alti teoreticieni interpreteaza normativele teoriei jourilor ca si cum ar sfatui agentii ce sa faca in contexte strategice pentu a-si maximize utilitatea. Din fericire pentru scopurile noastre, toate aceste metode de gandire despre posibilele facilitate ale teoriei jocurilor sunt compatibile cu interpretarea tautologica a utilitatii maximizate. Diferentele filozofice nu sunt oricum ideale din perspectiva muncii unui teoretician al teoriei jocurilor. Dupa cum vom vedea intr-o sectiune ce va urma, aceia care spera sa foloseasc teoria jocurilor pentru a explica ratiuni strategice, in opozitie cu strategiile comportamentale, infrunta cateva probleme filozofice si practice.
Din moment ce teoria implica formalitati rationale, trebuie sa avem o ratiune clara atunci cand ne gandim la maximizarea utilitatii in teermeni matematici. Un asemenea dispozitiv se numeste utilitatea functiei. Mapa utilitatilor pentru un agent se numeste o 'functie' pentru ca mapa ordoneaza preferintele in numere reale. Sa presupunem ca agentul x prefera ca legatura a sa se lege ce legatura b si ca legatura b sa se lege cu c. Apoi noi indexam astea intr-o lista de numere reale, unde functia va alege cea mai stransa legatura intre cele mai mari numere din lista, cea de-a doua legtura stransa cu urmatoarele numere mari din lista s.a.m.d.:
Bundle a>>3
Bundle b>>2
Bundle c>>1
Singura proprietate scoasa in evidenta de aceasta functie este ordinea. Magnitudinea acestor numere este irelevanta, darn u trebuie ca x sa aiba de 3 ori mai multa utilitate de la legatura a decat are de la legatura c. Astfel se poate reprezenta exact aceeasi functie de utilitate ca cea de mai sus: bundle a>>7.326
bundle b>>12.6
bundle c>>-1.000.000
Numerele aflate astfel intr-o functie de utilitate nu masoara astfel nici o cantitate. O functie de utilitate in care magnitudinea conteaza se numeste 'cardinal'. Oricand cineva se refera la o functie de utilitate fara sa specifice tipul acesteia trebuie sa presupunem ca este una ordinala. Acestea sunt tipurile de care vom avea nevoie pentru primul set de jocuri pe care il vom examina. Mai tarziu cand vom veni sa vedem cum sa rezolvam jocurile care implica diversificarea va trebui sa construim functiile de utilitate cardinale. Tehnica pentru acest lucru a fost data de von Neumann& Morgenstern (1947) si a fost un aspect esential al inventiei lor la teoria jocurilor.
Jocuri si informatii
Toate situatiile in care cel putin un agent poate doar sa actioneze pentru a-si maximize utilitatea prin anticiparea (fie constient, sau doar implicit prin comportament) raspusurilor actiunilor sale de catre unul su mai multi agenti se numeste joc. Agentii implicate in joc sunt numiti jucatori. Daca toti agentii au actiuni optimale indiferent de c ear face ceilalti, ca si in situatiile parametrice, in conditii de monopol sau in competitia perfecta putem modela acesta fara a apela la teoria jocurilor altfel vom avea nevoie de el.
Presupunem ca jucatorii sunt rationali din punct de vedere economic. Aceasta rationalitate poate fi in unele cazuri computerizata intern de catre agent. In alt cazuri poate fi doar implicate in dispozitii comportamanetale construite prin selectie naturala, culturala sau economica. In particular in alegerea unei actiuni noi cerem nonnecesitatea deliberarii constiente sau altfel. Noi credem ca actiunea a fost luata cand o alta actiune alternative era valabila, in cateva sensuri de valabilitate stabilita normal de contextul analizei particulare.
Fiecare jucator dintr-un joc se infrunta cu o alegere pe langa doua sau mai multe strategii. O strategie este predeterminata de program de joc care ne spune ce alegere sa facem ca raspuns la fiecare strategie ce poate fi folosita de alti jucatori. Semnificatia frazei italice va deveni aici clara cand vom lua exemple din jocul urmator.
Un aspect crucial al specificatiilor unui joc implica informatii pe care jucatorii le au cand aleg o strategie. Cele mai simple jocuri (din perspectiva unei structuri logice) sunt acelea in care agentii au informatii perfecte, insemnand ca la fiecare punct in care strategia fiecarui agent ne spune ca trebuie sa actionam, si stie ca orice s-a intamplat in acel joc pana la acel punct. Un joc de mutari secventiale in care ambii jucatori urmaresc toata actiunea (si cunosc regulile). Prin contrast exemplul jocului trecerea-podului ilustreaza un joc cu informatie imperfecta, din moment ce fugarul trebuie sa aleaga un pod pe care s ail traverseze fara sa stie ce pod a ales urmaritorul s ail astepte, si urmaritorul ia deasemenea decizii in a ignora unele actiuni. Cum teoria jocurilor este despre actiuni rationale date de strategiile actiunilor semnificative ale altora, ar trebui s nu te surprinda cand ti se va spune in ce jocuri agentii au stiut sau nu au stiut despre actiunile celorlalti ceea ce determina o diferenta considerabila logicii analizei noastre, asa cum vom vedea.
Arbori si matrici
Diferenta dintre jocurile cu informatie perfecta sau imperfecta este strans legata de (desi cu siguranta nu este identic!) o distinctie intre modurile de a reprezenta jocul ce este bazat pe o ordine de joc. Hai sa incepem prin a face distinctia intre o miscare secventiala a jocului ca fiind una in care jucatorii isi aleg strategiile unul dupa altul, si jocurile cu miscari simultane ca fiind una in care jucatorii isi aleg strategiile in acelasi timp. Asta nu este tocmai in regula, oricum, pentru ca ceea ce este de o importanta strategica nu este ordinea temporala de evenimente, ci de faptul cand jucatorii stiu despre alti jucatori ca actioneaza relative trebuie sa faca si propriile alegeri. De exemplu , daca doua firme concurente planuiesc sa faca campanii publicitare, una din ele poate sa modifice strategia lunara inaintea celeilalte; dar daca nici una din ele nu stie ce a facut cealalta sau ce va face pana cand isi vor face propriile planuri, acesta fiind un joc de actiuni simultane. Sahul, prin contrast, este jucat normal ca un joc de actiuni secventiale: se poate vedea ce a facut oponentul inainte sa iti fi ales urmatoarea ta actiune.
A fost spus mai sus ca diferenta dintre actiunile simultane si cele secventiale ale jocurilor nu este identica cu diferenta dintre informatie perfecta si informatie inperfecta a jocurilor. Explicand de ce este asa este o buna modalitate de a realiza o intelegere completa a acestor doua concepte. Dupa cum actiunile simultane au fost caracterizate in paragraful anterior este adevarat ca toate actiunile simultane fac parte din jocurile cu informatie imperfecta. Oricum cateva jocuri trebuie sa contina mixuri de actiuni secventiale sau simultane. De exemplu, doua firme actioneaza independent in strategiile de marketing si in secret una fata de cealalta, dar apoi se angajeaza in competitia preturilor stiind una de cealalta. Daca strategia optima de marketing a fost partial sau total dependenta de ceea ce se astepta sa se intample in jocul preturilor, atunci cele doua strategii vor trebui analizate ca pe un joc simplu in care o etapa a jocului secvential a urmat o etapa a unui joc simultan.
Toate jocurile care implica etape mixte de acest gen sunt jocuri cu informatie incompleta. Jocurile cu informatie completa denota cazuri in care nu sunt actiuni simultane (si in care nici un jucator nu uita ceea ce s-a intamplat in trecut).
A fost spus mai devreme ca jocurile cu informatie completa sunt cele mai simple (logice )tipuri de joc. Este asa pentru ca in astfel de jocuri (atata timp cat jocurile sunt finite, adica, terminate dupa un numar cunoscut de iteratii) jucatorii si analistii pot folsi o procedura directa pentru a prevedea veniturile ce vor urma. Intr-un astfel de joc un jucator rational alege prima actiune prin a considera fiecare serie de raspunsuri ce vor rezulta din fiecare actiune ce poate fi abordata. Atunci se poate intreba care dintre veniturile finale disponibile i-ar aduce utilitatea cea mai mare, si alege actiunea care incepe lantul ce duce la aceste venituri. Acest proces este numit inductie inversata.
Vom avea mult mai multe de spus despre inductia inversata si depsre proprietatile ei intr-o sectiune viitoare (cand vom discuta si despre echilibru si echilibrul selectiei). Pana acum am descris-o doar ca sa o putem folosi in introducerea a doua tipuri de instrumente matematice folosite sa reprezinte jocurile arbore. Un joc-arbore este un exemplu a ceea ce matematicienii numesc graf directionat. Este un set de noduri conectate in care liniile au o directie. Putem desena arbori de la capatul e sus al paginii pana la cel de jos sau de la stanga la dreapta.
In primul caz nodurile din prima parte a paginii sunt interpretate ca find cele care incep o secventa a unei actiuni. In cazul arborelui desenat de la stanga la dreapta nodurile din partea stanga sunt prioritare pentru secventa din partea dreapta. Un arbore neetichetat are urmatoarea structura:

Momentul reprezentarii jocurilor folosind arbori poate fi cel mai bine reflectat vizualizand utilitatea lor in suportul motivarii inductiei inversate. Doar imaginandu-ne ca jucatorul (sau analistul) incepand de la sfarsitul arborelui unde sunt impartite veniturile, si apoi lucrand invers, cautand seturi de strategii care descriu calea ce ar conduce spre ele. Din moment ce functia de utilitate a unui jucator indica veniturile pe care acesta le prefera putem sti deasemenea si calea pe care o prefera acesta. Bineinteles ca nu toate caile vor fi accesibile pentru ca celalalt jucator are deasemenea un rol in selectarea drumului si nu va actiona intr-un mod care i-ar diminua veniturile. Vom prezenta cateva exemple de aceste selectii de cai interactive si tehnici detaliate dupa ce vom descrie o situatie in cate putem folosi un arbore.
Arborii sunt utilizati pentru a reprezenta jocuri secventiale, pentru ca ei arata ordinea in care sunt luate actiunile de catre jucatori. Jocurile sunt reprezentate prin matrici si mai rar prin arbori. Acesta este al doilea tip de instrument matematic folosit in reprezentarea jocurilor. Matricile, spre deosebire de arbori, arata pur si simplu veniturile , tinand cont de functia de utilitate in termenii impusi, pentru fiecare combinatie posibila de strategii ce poate fi folosita de jucator. De exemplu are sens sa folosim joc de rau-trecator din sectiunea 1 intr-o amtrice, deoarece in acel joc atat fugarul cat si urmaritorul au dreptul la o singura miscare fiecare, si fiecare alege miscarea netinand cont de ce a ales celalalt. Aici este o parte a unei matrici:
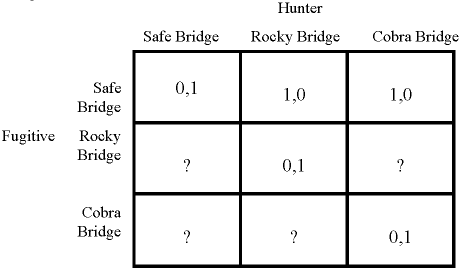
Cele 3 strategii posibile ale fugarului sunt in randurile din matrice. Similar, cele 3strategii posibile ale urmaritorului formeaza coloanele matricii. Fiecare celula a matricei arata - sau mai degraba ar arata daca matricea ar fi completa - un venit definite de platile jucatorilor. plata unui jucator este pur si simplu un numar atribuit de catre functia de utilitate a corespondentei dintre veniturile totale si veniturile in cauza. Pentru fiecare venit liniile sunt listate intotdeauna primele pentru ca apoi sa fie urmate de coloane. Astfel de exemplu, coltul din stanga sus arata cand traverseaza fugarul podul cel mai sigur si ca urmaritorul asteapta acolo, fugarul primeste un venit 0um si urmaritorul venitul 1um. Noi putem interpreta asta referindu-ne la functia de utilitate, care in acest joc este foarte simpla. Daca fugarul trece raul in siguranta el primeste un venit de 1um; daca nu va primi 0um. Daca fugarul nu reuseste, fie din cauza ca e impuscat de vanator, lovit de o stanca, sau ranit de un sarpe, atunci vanatorul primeste un venit de 1um, si fugarul va fi rasplatit cu 0um.
Vom explica in cateva cuvinte partile matricii care au fost completate, si apoi vom spune de ce nu putem completa si restul. Oricand vanatorul asteapta pe podul ales de fugar , acesta din urma este impuscat. Astfel veniturile vor fi reprezentate de vectorul (0 ) . Ele pot fi gasite pe diagonala matricii de deasupra coltului din stanga sus. De fiecare data cand fugarul alege sa traverseze podul cel sigur iar vanatorul astepta la alt pod, fugarul va trece podul in siguranta, acesta din urma va avea un venit dta de vectorul (1 ) . Aceste doua venituri sunt reprezentate in cele doua celule secundare din linia de sus. Toate celelalte celule sunt marcate cu semen de intrebare. De ce? Problema este ca fugarul traverseaza fie podul stancos sau pe podul cobrelor introducand astfel factori parametrici in joc. In aceste cazuri el risca sa fie ucis, producand astfel un venit reprezentat de vectorul (0 ) independent de orice actiune ar fi intreprinsa de vanator. Inca nu avem suficiente concepte introduse pentru a putea arata cum sa reprezentam aceste venituri in functie de functia de utilitate - dar in momentul in care terminaseram, si astfel vom avea si cheia ce rezolva puzzle-ul nostrum.
Jocurile matriciale se refera la forme- normale sau strategice, si jocurile ca si arborii sunt referiti ca forme - extinse ale jocurilor. Cele doua tipuri de jocuri nu sunt echivalente, pentru ca jocurile cu forme extinse contin informatii - despre secvente de joc si nivelul de informatie al jucatorilor despre structura jocului - ceea ce un joc cu forma strategica nu poate. In general jocul strategiei poate fi reprezentat prin cateva jocuri extensive, asa ca un joc strategic este cel mai bine gandit ca fiind un set de jocuri extensive.
Incertitudine, risc si echilibrul secventia
Toate jocurile prezentate pana acum au implicat jucatori ai strategiilor pure, in care fiecare cauta o singura actiune optima care sa fie cea mai buna replica a actiunilor celorlalti. Oricum deseori satisfactia unui jucator este obtinuta prin strategii mixte. Mixul este necesar cand nu avem strategii pure care sa maximizeze utilitatea jucatorilor in ciuda tuturor strategiilor oponente. Jocul cu treaversarea raului exemplifica acest lucru. Dupa cum am vazut puzzle-ul din acel joc consta in faptul ca fugarul este motivate sa aleaga un atat de potrivit incat urmaritorul sa isi asume riscul de a multiplica acea motivatie. Astfel fugarul poate scapa doar daca urmaritorul lui nu poate prevede care va fi podul folosit. Simetria din logica motivatiilor celor doi jucatori ne arata ca fugarul isi poate lua prin surprindere urmaritorul doar daca fugarul se poate lua prin surprindere pe sine insusi.
Presupunem ca ignoram rocile si cobrele pentru un moment si ne imaginam ca podurile sunt toate la fel de sigure. Presupunem de asemenea ca fugarul nu isi cunoaste urmaritorul intr-un mod special astfel incat sa aleaga un drum care sa nu fie ghicit de urmaritor. In acest caz cea mai buna alegere a fugarului este sa arunce cu zarul a carui parti sa reprezinte un alt pod. Astfel el trebuie sa isi preintampine gandurile de a folosi orice pod va fi ales prin acest mod intamplator. Aceasta fixeaza sansele supravietuirii sale indifferent de ce va face urmaritorul; dar din moment ce urmaritorul nu are nici un motiv sa prefere o alta strategie pura sau mixta, si cum in orice caz vom presupune ca aceasta situatie va fi simetrica cu aceea a fugarului, putem presupune ca a va arunca zarul in aceasta privinta. Fugarul are acum posibilitatea mai mare de a scapa iar sansele urmaritorului de a-l prinde vor fi mai mici. Fugarul nu poate imbunatati aceste sanse daca vanatorul este rational, asa ca cele doua strategii vor construe echilibrul lui Nash.
Acum vom reintroduce factorii parametrici, cum ar fi, pietrele care cad pe podul nr.2 si cobrele de pe podul nr.3. Iarasi presupunem ca fugarul este sigur ca va traversa in siguranta podul nr.1, ca are sanse de 90% sa treaca podul nr.2, si 80% sanse sa treaca podul numarul 3. Putem rezolva acest nou joc daca facem presupuneri despre functiile de utilitate a celor 2 jucatori. Presupunem ca jucatorului 1, fugarului, ii pasa doar de viata sau moarte (si ca prefera viata in locul mortii) in timp ce urmaritorul vrea doar sa raporteze moartea fugarului si nu sa raporteze fuga acestuia. In acest caz fugarul ia pur si simplu situatia de intamplare si o cantareste luand in considerare diferiti parametrii de pericol de pe cele 3 poduri. Optiunea de a allege oricare pod trebuie gandit ca pe o loterie a posibilelor venituri ale fugarului, in care fiecare loterie are venituri diferite in modul de prezentare a fuctiei de utilitate.
Echilibrul lui Nash este acea strategie care asigura maximizarea castigului fiecarui jucator cu strategia aleasa si tinand cont de strategiile alese de ceilalti jucatori.
Luam in considerare problema din punctual de vedere al urmaritorului. Acesta va utiliza strategia de NE cand alege probabilitatile mixte in legatura cu cele trei poduri care il face pe fugar sa fie indiferent la posibilele strategii pure. Podul cu roci este de 1.1 ori mai periculos pentru el decat podul cel sigur. Astfel este indiferent in alegerrea oricaruia dintre cele 2 poduri cand sunt sanse de 1.1 ori mai mari ca urmaritorul sa il astepte pe podul cel sigur decat pe cel cu roci. Podul cu cobre este de 1.2 ori mai periculos pentru fugar decat cel sigur. Astfelk el va fi indiferent in a alege intre cele doua poduri cand probabilitatea ca urmaritorul sa il astepte pe podul cel sigur este de 1.2 ori mai mare decat daca l-ar astepta pe podul cu cobre. Atunci urmaritorul isi minimizeaza sansa de supravietuire pe oricare din poduri prin ajustarea probabilitatilor p1 si p2
s1 (1-p1 s2(1-p2)
daca p1+p2=1 putem rescrie ecuatia de mai sus: s1x p2=s2xp1
p1/s1=p2/s2
Apoi urmaritorul isi gasete strategi prin rezolvarea urmatoarelor ecuatii:
1(1-p1 0.9(1-p2)=(1-p3)
p1+p2+p3=1
p1=49/121
p2=41/121
p3=31/121
Acum functiile f1,f2,f3 rprezinta probabilitatile cu care fugarul allege podul respective.
s1 x f1 = s2 x f2 = s3 x f3
1 x f1 = 0.9 x f2 = 0.8 x f3
f1 + f2 + f3 = 1
f1 = 36/121
f2 = 40/121
f3 = 45/121
Aceste doua seturi de probabilitati arata fiecarui jucator cum ssa isi evalueze strategia inainte de a face o alegere.
Am putut sa rezolvam acest joc pentru ca am aranjat functiile de utilitate in asa fel incat sa fie de suma zero sau competitive.
|