Proiectarea Asistata de Calculator in domeniul circuitelor electronice

Proiectarea Asistata de Calculator în domeniul circuitelor electronice 1. Arhitectura PAC - Module, functii, componente

Istoricul tehnologiei de Proiectare Asistata de Calculator, numita în continuare PAC

Proiectarea Asistata de Calculator, cu titulatura engleza Computer-Aided Design sau prescurtat CAD, îsi are începuturile în anii 1950, în laboratoarele MIT (Massachusetts Institute of Technology). Aceste cercetari au condus la evolutia ulterioara a produsului software APT (Automatically Programmed Tool), destinat prelucrarilor pe masini cu comanda numerica.

În anul 1965, laboratoarele Bell Telephone au anuntat aparitia sistemului de afisare Graphic1 destinat dispunerii componentelor electronice în cablaje, proiectarii de scheme, editarii de texte. Sistemul Graphic1 utilizeaza un terminal Dec 340 si un procesor de control PDP5, conectat la un calculator IBM 7094, deci având o procesare distribuita între statii locale de lucru si un calculator gazda central.

În 1966, divizia de componente a IBM a descris un sistem care asista proiectarea modulelor de circuite integrate hibride. Sistemul Gold a fost implementat pe un terminal condus de un mic calculator Spectra 70/25, capabil sa interactioneze cu un calculator de putere mare.

Majoritatea lucrarilor PAC au fost elaborate în prima jumatate a anilor '70, punând bazele sistemelor de azi. Produsele software PAC sunt adecvate problemelor ingineresti din domeniile mecanicii, chimiei, electronicii si arhitecturii. În domeniul electronicii, s-au dezvoltat sisteme PAC cum ar fi Spice (Simulation Program Integrated Circuits Electronic); în domeniile mecanicii si arhitecturii - "Integrated Civil Engineering System" utilizând teoria elementului finit; în domeniul productiei - "Production Automation Project". Apare termenul CAE - Computer-Aided Engineering, utilizat pentru a include aspectele de analiza si optimizare ale proiectului.

Sfârsitul anilor '70 poate fi caracterizat ca fiind momentul de trecere a algoritmilor de Proiectare Asistata de Calculator din mediul stiintific catre zona economica, transformându-se într-un instrument, nu numai atractiv, dar si indispensabil. S-au facut eforturi de integrare a metodelor PAC în proiectare si în tehnologiile din industrie, adica de integrare CAD - CAM (Computer-Aided Manufacturing). CAM porneste de la datele produse de procesul de proiectare, dar nu face parte din procesul de proiectare propriu-zis.

De asemenea, CAT (Computer-Aided Testing), CAP (Computer-Aided work Planning), CAM (Computer-Aided Maintenance) sunt în aceeasi situatie: pornesc de la datele produse de procesul de proiectare, dar nu fac parte din procesul de proiectare propriu-zis.

Clasificari ale sistemelor PAC se pot face:

Dupa modul de executie a programelor:

- "time-sharing" - mai multe programe independente se executa pe acelasi calculator; utilizatorii folosesc în comun doar unitatea centrala;

- "system-sharing" - mai multi utilizatori lucreaza cu un program de aplicatie comun utilizând acelasi calculator, aceeasi baza de date; utilizatorii folosesc în comun resursele sistemului PAC.

Din punct de vedere hardware:

sisteme independente - statii grafice de lucru

sisteme terminale - legate la un calculator gazda si la baza lui de date.

Din punct de vedere software

- sisteme la cheie - au un set predefinit de functii, operând doar pe un hard specializat, cu o capacitate limitata de interfatare cu alte sisteme prin formatul standard al datelor;

- sisteme deschise - uzual transferabile pe un numar mare de tipuri de sisteme lucrând cu o varietate de terminale grafice

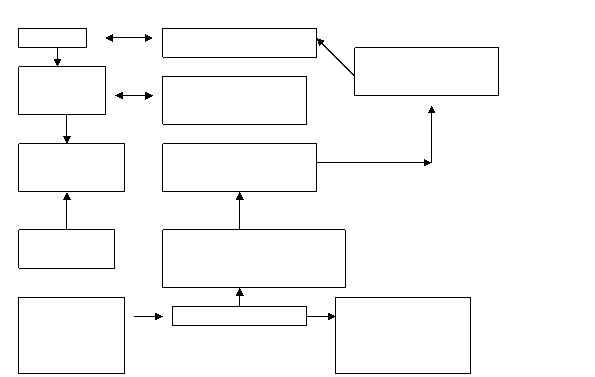
Proiectarea Asistata de Calculator furnizeaza un suport pentru simularea pe calculator a procesului de proiectare. Pentru a stabili conceptele modelarii procesului de proiectare, trebuie definit întâi sistemul global în care PAC lucreaza, adica:

- baza de metode sub forma de biblioteca de programe,

- baza de date,

- sistemul de comunicatie (interfata).

Biblioteca de metode (programe) contine module utilizate pentru functiile elementare ale sistemului (baza de date, dialogul, date de intrare-iesire, grafica) si module care reprezinta domeniul de aplicatie.

Baza de date contine module pentru introducere date, de garantare a integritatii si consistentelor în baza de date si cereri de informatii din baza de date.

Interfata sau Subsistemul de comunicatie include module pentru dialog (comenzi adresate sistemului PAC si mesaje transmise utilizatorului).

Proiectant / utilizator

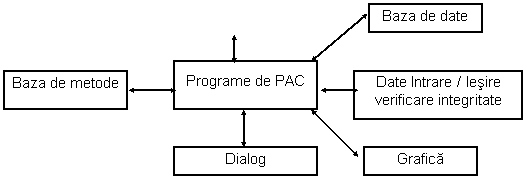
Figura 1 Arhitectura sistemului de Proiectare Asistata de Calculator

(Interfata de comunicatie)

(Interfata baza de metode)

(Interfete baza de date)

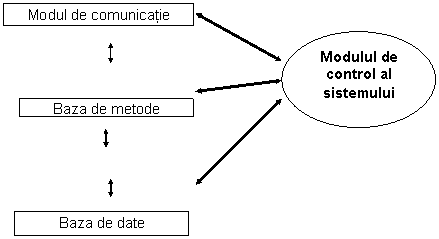
Figura 2. Componente PAC

2. Definirea procesului de proiectare

Teoria proiectarii furnizeaza o baza puternica pentru formalizarea proceselor si a cunostintelor activitatii de proiectare si modeleaza proiectarea ca o transformare din spatiul functiilor (specificatiile sunt descrise prin functii) în spatiul atributelor; solutiile proiectarii fiind descrise prin atribute.

Procesul de proiectare este structurat ca o procedura iterativa, constând din 6 faze:

formularea cerintelor,

definirea problemei,

sinteza, analiza,

optimizarea,

evaluarea,

prezentarea.

În continuare, sunt descrise fazele procesului de proiectare, asa cum sunt ele abordate în aceasta lucrare.

Formularea cerintelor consta în identificarea problemei si definirea specificatiilor. O parte din specificatii sunt constrângeri exprimate ca plaja de valori si criterii. Aceste constrângeri sunt folosite pentru a compara variantele proiectului; cel mai bun proiect este cel care raspunde cel mai bine constrângerilor si care are cea mai buna combinatie a valorilor criteriilor. Aceasta reprezinta definirea problemei.

Urmatorii pasi (sinteza, analiza si optimizarea-evaluarea) au un caracter iterativ.

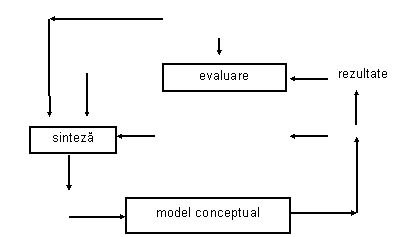
Sinteza. Un proiect este sintetizat sau creat, determinându-se componentele sistemului si caracteristicile lor pentru a raspunde tuturor constrângerilor.

Analiza. Consta în determinarea rezultatelor proiectului în urma rezolvarii setului complex de ecuatii diferentiale ce corespund criteriilor proiectului si constrângerilor aferente. Rezultatele analizei pot fi exprimate în forma tabelara sau grafica. Daca analiza arata ca una din constrângeri nu este îndeplinita sau ca un criteriu poate fi îmbunatatit, proiectul este modificat (se reia faza de sinteza) si reanalizat.

Evaluarea este tot o analiza care implica construirea unei tehnologii si a unui proiect pentru teste experimentale. Modelul actual este testat si comparat cu constrângerile pentru fezabilitate si se fac masuratori asupra variabilelor criteriilor. În cazul în care constrângerile nu sunt îndeplinite, se revine la faza de sinteza, în functie de avantajele economice ale reproiectarii - daca îmbunatatirile vor costa mai mult decât beneficiile posibile, nu se face reproiectarea. Aceste iteratii se pot efectua de mai multe ori, înainte de a se ajunge la un proiect fezabil sau optim.

(specificatii proiect)

modificari

aspecte tehnologice analiza

cunostinte

Figura 3. Reprezentarea procesului de proiectare

Asa cum a fost prezentata mai sus, proiectarea este un proces serial, în care analizele si fazele prin care trece un produs pâna la executie, se efectueaza în mod serial. Un proiect poate trece de faza de proiectare, putând fi respins la faza de executie; o modificare ulterioara pentru a îmbunatati performantele necesare fazei de executie, poate sa determine esuarea performantei de proiectare.

În ultimii ani, s-a demonstrat tot mai mult faptul ca procesul de proiectare trebuie sa se desfasoare concurential, simularea tuturor implicatiilor produse în fazele de executie putând fi prevazute înca din faza de proiectare conceptuala. Proiectul evolueaza satisfacând o cerinta sau alta pâna când se gaseste un proiect fezabil.

Modelul conceptual trebuie sa contina si informatii necesare marketingului, executiei, testarii si întretinerii produsului; aceste cerinte ilustreaza rolul bazelor de date în aplicatiile PAC. Un alt aspect vizeaza si situatiile când cunostintele nu sunt certe.

Abordarea recenta, având ca obiectiv modelarea procesului de proiectare, se bazeaza pe conceptul de proiectare concurenta, în care toate fazele de proiectare se abordeaza simultan si orice proiect se bazeaza nu doar pe rezultatul analizei, ci pe un pachet total de rezultate. Se presupune ca proiectarea concurenta va reduce oscilatiile ce apar în procesul de proiectare mentionat anterior, ceea ce presupune analiza functionala concomitenta cu cea tehnologica, pentru ca sa se evite situatiile actuale când, de multe ori, un proiect acceptabil functional poate fi gasit inacceptabil tehnologic. Proiectarea concurenta impune ca toate analizele sa se efectueze simultan, la toate iteratiile.

Rezultatul activitatii de proiectare se constituie în baza de date a proiectului. Aceasta contine rezultatele fazei de sinteza si se completeaza cu rezultatele analizei.

Sinteza proiectului este, de obicei, efectuata de utilizator. Pentru aceasta, el trebuie sa dispuna de un model conceptual al obiectelor manipulate de sistemul PAC si sa cunoasca starea procesului PAC. Utilizatorul trebuie sa aiba o întelegere conceptuala a metodelor implementate în sistem, ca programe de analiza, si a modului cum aceste metode afecteaza obiectele manipulate de sistem. Cu aceste cunostinte, utilizatorul poate formula specificatiile urmatorilor pasi ce vor fi parcursi si va transmite aceste cereri sistemului PAC. În anumite cazuri, sinteza este, cel putin partial, localizata în interiorul sistemului PAC. Pentru astfel de produse dintr-un anumit mediu, si anume, în sistemele bazate pe inteligenta artificiala, este posibil sa se formuleze un algoritm de sinteza.

Din punct de vedere conceptual, componentele unui sistem PAC sunt:

- baza de metode (sub forma de programe),

- modul de comunicatie cu utilizatorul,

- baza de date,

- modul de supervizare si control, care realizeaza functiunile PAC ( sinteza, analiza, transformare, evaluare, reprezentare); sistemul PAC propriu zis realizeaza analiza si transformarile utilizând biblioteca de metode; starea procesului este reprezentata în baza de date, rezultatele sunt prezentate utilizatorului în forma grafica sau tabelara, pentru a facilita comparatiile necesare aprecierii criteriilor)

Specificatiile de probleme sunt transmise de utilizatorul sistemului PAC prin comenzi, interogari exprimate într-un limbaj specific.

Lucrarea reprezinta o încercare de formalizare a procesului de proiectare în domeniul circuitelor electronice nelineare, astfel încât inginerul proiectant începator sa deprinda abordarea sistemica prezentata.

În procesul de însusire a tehnicii de proiectare, analiza circuitelor electronice nelineare reprezinta primul pas. Astfel, în subcapitolele 2-4, este prezentat modul de însusire a formalizarii si sistematizarii notiunilor necesare în fazele de formulare a problemei, de analiza si optimizare a simularii functionarii circuitelor electronice nelineare, si anume, artificiile necesare linearizarii circuitului, definirea circuitelor echivalente în curent continuu, în curent alternativ si timp, determinarea sensitivitatii pentru stabilirea influentei tolerantelor asupra functionarii circuitului.

Scopul acestui subcapitol este de a prezenta tehnicile numerice de baza, artificiile care sunt necesar a fi facute, pornind de la fundamentele teoretice ale analizei.

Astfel, sunt elaborati si explicati algoritmi de modelare - simulare în domeniul circuitelor electronice: pornind de la topologia circuitului, se "inspecteaza", în mod automat, nodurile circuitului si se scriu, tot în mod automat, relatiile dintre curenti si tensiunile la noduri (legile Kirchoff) denumite ecuatii nodale. O data generate ecuatiile nodale, se poate trece la rezolvarea acestora pentru a determina solutia, adica tensiunile în nodurile circuitului. Dupa determinarea tensiunilor în nodurile circuitului, pentru circuitul nelinear, se pot realiza analiza de semnal mic, analiza de curent continuu, analiza în curent alternativ, analiza în domeniu timp. De asemenea, se pot determina sensitivitatile circuitului si optimiza proiectarea acestuia.

În capitolele 5-7, este prezentata abstractizarea cunostintelor referitoare la functionarea circuitelor electronice nelineare, abstractizare necesara procesului de generare a regulilor pentru crearea bazei de cunostinte.

2.1. Algoritmi de modelare - simulare în domeniul PAC destinat circuitelor electronice

Deoarece calculatorul are un rol tot mai accentuat în analiza si simulare, deci în proiectare, devine tot mai important pentru un inginer sa fie obisnuit nu numai cu fundamentele teoretice ale analizei si proiectarii, dar si cu tehnicile numerice de baza, care îi permit sa utilizeze mai eficient calculatorul. În acest scop, nu este suficienta cunoasterea utilizarii programului de analiza, care simuleaza comportamentul circuitului, rezolvând limitarile de proiectare. Inginerul care utilizeaza un asemenea program, dar nu este familiarizat cu tehnicile de baza, teoretice si numerice, folosite de program, nu este pregatit sa evalueze validitatea simularii. Inginerul care ia deciziile de proiectare bazându-se pe simularea facuta de calculator trebuie sa fie sigur de exactitatea simularii.

2.1.1. Algoritmi PAC utilizati pentru formularea ecuatiilor nodale

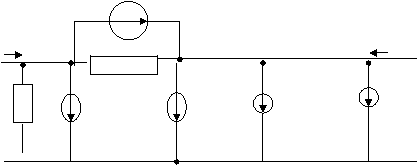
Prima faza în proiectarea asistata a unui circuit este cea de determinare a tensiunilor în nodurile circuitului, v_k (t). Pentru aceasta, în mod automat, se analizeaza topologia circuitului si se scriu ecuatiile nodale având ca fundament legile Kirchoff, KCL si KVL, pentru curenti si tensiuni.

Pentru un circuit având n noduri si n-1 ramuri, ecuatiile nodale sunt scrise automat, fiind de forma:

S_j y_jk v_k (t) = i_k (t)

unde n - numar noduri,

y_kk - S admitantelor conectate la nodul k,

y_jk - negativul S admitantelor conectate între nodul j si k (daca între nodurile j si k nu exista admitanta, y_jk este 0);

i_k (t) S tuturor curentilor intrând în nodul k, a curentilor în sursele de curent independente, a curentilor prin sursele de tensiune independente, si a curentilor initiali prin inductante,

v_k (t) - tensiunile la noduri, necunoscute.

Transformari specifice PAC

Scrierea automata a ecuatiilor se face dupa "inspectia" prealabila a circuitului. Existenta surselor de tensiune flotante introduce necunoscute suplimentare, una pentru fiecare sursa de tensiune, deci ecuatii suplimentare care sa exprime relatiile de ramura ale sursei respective, exprimate ca tensiuni la noduri. Pentru a se evita aceasta situatie, se procedeaza astfel: se aplica principiul V-shift care statueaza ca circuitul ramâne neschimbat, din punct de vedere al comportamentului, daca se deplaseaza sursa de tensiune în toate ramurile conectate la un capat al sursei; în acest caz, se poate face conversia sursei de tensiune flotante (neîmpamântate) cu circuitul echivalent, adica o sursa de curent de valoare V/R în paralel cu rezistenta ramurilor pentru care s-a aplicat principiul V-shift.

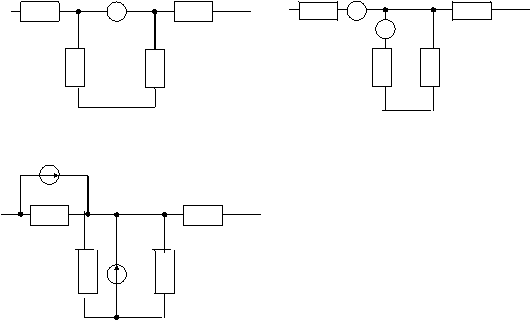
O exemplificare a acestui caz este prezentata în cele ce urmeaza. Fie reteaua de mai jos, unde sursa V poate fi deplasata fie în nodul 1, fie în nodul 2, astfel:

a)     ca sursa de tensiune, deci un nod si o ramura suplimentara, deci o necunoscuta în plus. Pentru a evita aceasta situatie, se utilizeaza artificiul de la punctul b.

b)    ca sursa de curent paralela cu rezistenta, de valoare V/R₁

a)    

R₁ - V + R₂ R₁ -V + R₂

1 2 1 2

V +

R₃ R₄ R₃ R₄

b)     V/R₁

R₁ 1 2 R₂

R₃ V/R₃ R₄

Figura 4. Ilustrarea principiului V-shift

Rezolvarea sistemului de ecuatii nodale

În calculul numeric, un rol important îl constituie utilizarea matricelor în exprimarea ecuatiilor KCL si KVL si a relatiilor de ramura, datorita facilitatilor pe care le ofera calculul matricial.

Folosind notatiile matriciale, ecuatiile nodale devin:

YI = V

(2)

unde Y - matricea admitantelor, I - vectorul curent, V - vectorul tensiune.

În cazul circuitelor cu mai multe noduri, de altfel un caz obisnuit, rezolvarea ecuatiilor prin metoda eliminarii Gauss, deci a substitutiei, pornind de la ecuatiile nodale, nu este eficienta, necesitând mult timp pentru rezolvare. De aceea, aceasta metoda nu este utilizata direct printre algoritmii numerici, discutati în aceasta lucrare.

Având în vedere ca, pentru oricare pereche de noduri j si k, între care nu exista conexiune directa, valoarea admitantei este nula, rezulta ca matricea admitantelor Y este o matrice rara. Pentru rezolvarea sistemului de ecuatii, se folosesc tehnicile specifice ale matricelor rare, si anume factorizarea low-upper (LU).

În vederea rezolvarii sistemului de ecuatii nodale, în care matricea admitantelor Y este o matrice rara, se procedeaza, în prealabil, la factorizarea matricei admitantelor [12,16,17].

Factorizarea matricei admitantelor Y consta în determinarea a 2 matrice,

matricea triunghiulara L (lower) si

matricea triunghiulara U (upper).

Sistemul de ecuatii devine LUV = I.

Rezolvarea acestui sistem se face în doi pasi:

LI* = I ( substitutia înapoi) determinarea solutiei intermediare I*.

Solutia intermediara a sistemului este: I* = L^-1 I.

UV = I* ( substitutia înainte) determinarea solutiei finale V.

Solutia sistemului este:

V = U^-1 L^-1 I*  (3)

2.1.2. Algoritmi PAC utilizati în analiza de semnal mic a circuitelor nelineare

În mod obisnuit, circuitele contin elemente nelineare, caracterizate de relatii de forma v = f (i) sau i = f (v).

Ecuatiile nodale, utilizând relatiile KCL si KVL, devin nelineare. O solutie analitica pentru circuite nelineare este practic imposibil de obtinut pentru ecuatii nelineare. Pentru a rezolva aceasta problema, este necesar sa se gaseasca un algoritm de linearizare a circuitului. Dupa linearizarea acestuia, este importanta studierea comportamentul circuitului la o variatie mica a intrarii, procedura denumita analiza de semnal mic a circuitelor nelineare.

Pasii de verificare a linearizarii propuse sunt:

determinarea circuitului echivalent, pentru care este necesara aplicarea artificiilor de linearizare;

definirea automata a relatiilor Kirchoff pentru reteaua echivalenta linearizata;

rezolvarea ecuatiilor pentru semnalul dat si verificarea convergentei solutiei;

incrementarea solutiei pentru mici variatii ale semnalului de intrare.

Determinarea circuitului echivalent linearizat consta în:

aproximarea elementelor nelineare cu circuite echivalente linearizate, de exemplu dioda este echivalenta cu o sursa de curent Isc în paralel cu R_N (rezistenta echivalenta cu sursele interne puse la zero, conform teoremei Norton)

determinarea valorilor elementelor circuitului echivalent linearizat în asa fel încât sa se asigure convergenta solutiei; procesul de determinare a valorilor elementelor circuitului echivalent linearizat este un proces iterativ, care converge spre solutie daca valorile determinate între 2 iteratii succesive sunt sensibil egale, adica eroarea produsa în aproximarile succesive considerate sa nu depaseasca o valoare impusa.

Determinarea valorilor elementelor circuitului echivalent linearizat se face folosind algoritmul iterativ Newton-Raphson, care consta în:

expandarea în serie Taylor a functiei nelineare i = f (v) în jurul unui punct din regiunea activa a caracteristicii I-V a acesteia

Pentru 2 iteratii (estimari) succesive l si l+1, ^l = f (v^l), iar i^{l + 1} = f (v^{l + 1}) = f (v^l) + (v^{l + 1} - v^l), unde este o conductanta, * v^l este o sursa de curent.

Deci, reteaua echivalenta linearizata este o conductanta G _eq în paralel cu o sursa de curent I _eq:

modelul rezultant este modelul linearizat al elementului nelinear;

tensiunea la orice iteratie i+1 se determina în functie de tensiunea la iteratia anterioara, în acest caz, l; când eroarea între tensiuni la iteratiile l si l+1 este suficient de mica, adica mai mica sau egala cu valoarea impusa, înseamna ca algoritmul converge, iar valorile sursei de curent si conductantei astfel stabilite, reprezinta valorile modelului linearizat, utilizat în oricare analiza. Algoritmul iterativ Newton Raphson necesita mult timp calculator si exista posibilitatea ca algoritmul sa nu convearga spre solutie, daca nu se lucreaza direct cu modelul linearizat, deoarece pentru evaluarea exponentialei la valori mai mari ale tensiunii s-ar putea produce depasiri; la fel si la determinarea valorii rezistentei în modelul linearizat, se poate ajunge la valori foarte mari, care sa produca probleme la rezolvarea ecuatiilor nodale.

De aceea, a fost important de gasit o procedura-artificiu, si anume algoritmi PAC pentru analiza de semnal mic [27], [28], [29].

Pentru elementele nelineare (cum ar fi dioda si tranzistorul), rezolvarea modelului linearizat clasic al acestora este, practic, imposibila.

Algoritmi PAC pentru analiza de semnal mic a circuitelor nelineare este o procedura fundamentala, utilizata pentru studierea comportamentului unei întregi clase de circuite, si consta în: introducerea de mici variatii în intrare; determinarea solutiei pentru toate variatiile intrarii, utilizând algoritmul Newton Raphson pentru fiecare variatie a intrarii, ceea ce presupune consum mare de timp calculator. De aici, ideea de a determina solutia ecuatiilor numai pentru valoarea initiala a intrarii si pentru valorile variatiilor intrarii, cu conditia ca intrarea i = 0, iar variatia intrarii sa fie mica în raport cu valoarea de baza i. Aceasta analiza se numeste analiza de semnal mic a circuitelor nelineare, deoarece mici variatii ale intrarii Di produc variatii mici ale iesirii.

Se determina reteaua linearizata corespunzatoare doar variatiilor micii ale intrarii Di (în situatia când intrarea i =0). Deoarece variatiile intrarii Di si a iesirii Dv sunt mici, în raport cu i sau v (valorile de baza), acest circuit se numeste circuit echivalent de semnal mic; elementul nelinear este echivalent cu o rezistenta a carei valoare este egala cu panta caracteristicii în punctul de operare (operating point v^op). Valoarea tensiunii în punctul de operare v^op se determina aplicând algoritmul Newton Raphson o singura data pentru intrarea i , cu Di = 0:

modelul linearizat de semnal mic al elementelor rezistive, utilizat în oricare analiza G= 1/.

Deci, analiza de semnal mic a circuitelor nelineare conduce la urmatoarea concluzie:

în loc sa se determine solutiile circuitului nelinear aplicând algoritmul Newton Raphson pentru fiecare valoare diferita i + Di, se determina valoarea tensiunii în punctul de operare v^op aplicând algoritmul Newton Raphson o singura data pentru intrarea i, cu Di = 0; elementele nelineare se înlocuiesc cu circuitele echivalente linearizate [11], [13

dupa aceasta, se seteaza i=0, elementele nelineare se înlocuiesc cu rezistentele echivalente de semnal mic, deci, rezulta un circuit linear de semnal mic;

se determina solutiile pentru circuitul linear de semnal mic rezultant, adica Dv pentru fiecare variatie Di;

se determina solutiile pentru circuitul nelinear, de forma v^op + Dv (conform principiului superpozitiei).

Observatie: Acelasi principiu (metoda) se aplica si în situatia tranzistorului. O data determinat punctul de operare (i_E, i_C, v_CB, v_EB), pentru mici perturbatii ale intrarii (excitarii) punctul de operare devine (i_E+Di_E, i_C+Di_C, v_CB+Dv_CB, v_EB+Dv_EB). Este mai sigur si mai usor sa se determine un singur punct de operare al circuitului linearizat, dupa care, în loc sa se reia analiza nelineara completa pentru a determina exact un alt punct de operare, adica o procedura nesigura si greoaie, se utilizeaza reteaua linearizata de semnal mic în punctul de operare determinat si se excita reteaua numai cu "perturbatii".

Urmatorul pas în analiza circuitelor îl constituie analiza sensitivitatilor, analiza importanta în siguranta fabricatiei circuitului, în studiul efectelor termice, în analiza statistica a defectiunilor sau sinteza circuitului. Situatia cea mai frecventa o constituie determinarea variatiei parametrilor circuitului datorita tolerantelor elementelor sau a schimbarilor de temperatura, efectelor îmbatrânirii sau a variatiei de frecventa [27], [29].

Ideea analizei porneste de la determinarea cazului cel mai defavorabil. Analiza cazului cel mai defavorabil presupune determinarea domeniului de valori posibile pentru iesiri, corespunzator domeniului de variatie a valorilor posibile a elementelor rezistive.

2.1.3. Algoritmi PAC utilizati în analiza de curent continuu a circuitelor nelineare

Analiza de curent continuu a circuitelor nelineare are ca scop determinarea marimilor de iesire în cazul variatiei excitatiei la intrare (notam intrarea V_i si iesirea V₀) si se desfasoara în urmatorii pasi:

se linearizeaza circuitul, prin înlocuirea elementelor nelineare cu circuitele echivalente linearizate;

se determina valoarea tensiunii în punctul de operare v^op aplicând algoritmul Newton Raphson o singura data pentru intrarea V_i , cu DV_i = 0;

în loc sa se determine solutiile circuitului nelinear, aplicând algoritmul Newton Raphson pentru fiecare valoare diferita V_i + DV_i,

se alege pasul variatiei excitatiei la intrare DV_I,

se seteaza V_i = 0, elementele nelineare se înlocuiesc cu rezistentele echivalente de semnal mic, rezultând deci un circuit linear de semnal mic;

se determina solutiile pentru circuitul linear de semnal mic rezultant, adica DV₀ pentru fiecare variatie DV_i;

se determina solutiile pentru circuitul linearizat, de forma V₀ = v^op+V₀ (conform principiului superpozitiei).

2.1.4. Algoritmi PAC pentru analiza în curent alternativ a circuitelor nelineare

Analiza în curent alternativ a circuitelor nelineare are ca scop determinarea functiei de transfer (magnitudine si faza) în cazul excitarii la intrare cu un semnal sinusoidal.

Studiul circuitelor sub excitatie sinusoidala este justificat din 2 motive:

multe circuite sunt proiectate sa lucreze sub excitatie sinusoidala (de exemplu, amplificatoarele audio, care nu numai ca trebuie sa reproduca fidel, dar sa si amplifice semnalul sinusoidal de intrare);

toate semnalele periodice pot fi reprezentate ca o suma de sinusoide, astfel încât, daca se stie raspunsul la un semnal sinusoidal, se poate determina raspunsul pentru orice semnal periodic.

În analizele anterioare, a fost necesara rezolvarea ecuatiilor diferentiale ce caracterizeaza circuitele, deci a fost necesara gasirea de metode de analiza numerica în stare sa realizeze aproximarea acestora.

În cazul analizei de curent alternativ, se descriu tehnici care evita rezolvarea ecuatiilor diferentiale [8], [9].

Forma generala a formei de unda sinusoidale este:

v(t) = V_m sin (wt + f), unde V_m - amplitudinea formei de unda, w frecventa, în radiani /sec.;

w p / T, unde T - perioada semnalului, f unghiul faza;

sau folosind identitatea Euler, v(t) = Ve^jwt , unde V este fazorul V = V_m e^jf

Dupa linearizare, o retea nelineara contine elemente de stocare L si C. Ecuatiile nodale pentru o astfel de retea sunt, în mod obisnuit, ecuatii diferentiale; dar, folosind notatiile de mai sus, ecuatiile diferentiale se transforma în ecuatii algebrice complexe, ecuatiile KCL devenind:

S_i a_ki I_i = (12)

Astfel, ecuatiile la noduri KCL pot fi scrise direct, utilizând curentii fazori de ramura.

Ecuatiile KVL devin:

V_i = S_i a_ki V_k

Astfel, ecuatiile KVL pot fi scrise direct, utilizând tensiunile fazoare de ramura si la noduri.

Ca urmare a scrierii ecuatiilor KVL folosind definitiile complexe, pentru ramurile circuitului linearizat, obtinem:

element rezistiv R (15a)

element capacitiv   impedanta Z_C (wC) = 1/ jwC (15b)

element inductiv impedanta Z_L (wC) = jwL (15c)

Ţinând seama de cele spuse pâna acum, analiza în curent alternativ a circuitelor nelineare se desfasoara în urmatorii pasi:

se linearizeaza circuitul, prin înlocuirea elementelor nelineare cu circuitele echivalente linearizate;

se determina valoarea tensiunii în punctul de operare v^op aplicând algoritmul Newton Raphson o singura data pentru intrarea V_i , considerata pentru curent continuu;

se determina valorile elementelor circuitului linearizat pentru punctul de operare determinat;

în loc sa se determine solutiile circuitului nelinear în intervalul de frecventa dat prin aplicarea algoritmului Newton Raphson, se procedeaza astfel:

- se alege pasul variatiei excitatiei la intrare DV_i, în urma esantionarii intervalului de frecventa;

- se scriu ecuatiile complexe KCL si KVL pentru circuitul linearizat, pentru fiecare punct de frecventa din interval;

se determina solutia sistemului, magnitudinea si faza marimilor de iesire, prin rezolvarea ecuatiilor complexe KCL si KVL pentru circuitul linearizat.

2.1.5. Algoritmi PAC pentru analiza în domeniu timp a circuitelor nelineare

Elementele de stocare sunt caracterizate, în domeniu timp, de relatii de tipul:

pentru capacitate i (t) = C v (t) sau v (t) = v (t₀) + i (t)dt,

pentru inductanta v (t) = L i (t) sau i (t) = i (t₀) + v (t)dt.

Circuitele care contin n elemente de stocare sunt caracterizate de ecuatii nodale de tip ecuatii diferentiale de ordinul n. Solutia numerica este reprezentata în [20], [21], [22], [23]:

Pasul 1. Esantionarea intervalului de timp în k pasi t₁ ...t_k-1 t_k unde pasul de integrare este h =t_k - t_k-1.

Pasul 2. Aproximarea solutiei utilizând algoritmul recursiv de integrare:

Euler forward y ^k+1 = y^k + h*f^k (16)

Euler backward y ^k+1 = y^k + h*f^k+1

În abordarea PAC, pentru fiecare moment k, elementele de stocare (capacitate sau inductanta) se reprezinta prin reteaua companion echivalenta.

Astfel, aplicând algoritmul de integrare pentru fiecare moment de timp t_k, reprezentarea elementelor de stocare devine:

capacitate

Circuitul echivalent al capacitatii este o rezistenta h/C în paralel cu o sursa de curent C/h v^k; solutia rezolvarii ecuatiilor integro-diferentiale pentru fiecare moment de timp t_k, este:

v ^k+1 = v^k + i ^k (17)

inductanta

Circuitul echivalent al inductantei pentru fiecare moment de timp t^k este o sursa de curent v^k; solutia rezolvarii ecuatiilor integro-diferentiale pentru fiecare moment de timp t_k, este:

i ^k+1 = i^k + v^k  (19)

Pasul 3. Repetarea algoritmului pentru toate momentele t_k , unde k = 1,2,... n, ceea ce reduce analiza în timp la o analiza în curent continuu repetata pentru toate momentele t_k; circuitul îsi modifica topologia si valorile pentru elementele de stocare asa cum s-a aratat mai sus.

2.1.6. Algoritmi PAC pentru determinarea sensitivitatilor circuitelor

Termenul de sensitivitate este utilizat pentru prezicerea situatiei celei mai defavorabile.

Determinarea sensitivitatilor circuitelor se face pentru a se stabili si analiza cazul cel mai defavorabil, reprezentat de variatia parametrilor circuitului datorat tolerantelor elementelor. Analiza cazului cel mai defavorabil presupune determinarea domeniului de valori posibile pentru iesiri pentru domeniul de variatie a valorilor posibile ale elementelor rezistive

Se defineste sensitivitatea circuitului în raport cu un element rezistiv R_k ca fiind:

normalizata = (R_k/Vo) dVo (R₁, R₂, ... R_n; i)/dR_k (21)

nenormalizata = dVo (R₁, R₂, ... R_n; i)/dR_k (22)

adica tensiunea de iesire Vo variind în raport cu R_k, conform derivatei partiale dVo în raport cu dR_k.

Sensitivitatea prezice comportamentul local, datorat schimbarilor valorii unui parametru si anume:

daca sensitivitatea > 0, cresterea elementului rezistiv determina cresterea tensiunii;

daca sensitivitatea < 0, cresterea elementului rezistiv determina scaderea tensiunii.

Astfel,

descresterea cea mai mare a iesirii se produce daca valoarea oricarei rezistente, având sensitivitatea negativa, a crescut peste valoarea limita superioara din domeniu sau de tolerante, în timp ce valoarea oricarei rezistente cu sensitivitate pozitiva a descrescut la limita inferioara din domeniu sau de tolerante;

cresterea cea mai mare a iesirii se produce daca valoarea oricarei rezistente, având sensitivitatea negativa, a descrescut peste valoarea limita inferioara din domeniu sau de tolerante, în timp ce valoarea oricarei rezistente cu sensitivitate pozitiva a crescut la limita superioara din domeniu sau de tolerante.

Rezolvarea pe calculator a problemei sensitivitatilor presupune simularea unui circuit adjunct, care foloseste principiul enuntat de teorema Tellegen în determinarea sensitivitatii.

Astfel, pornind de la relatiile KCL si KVL, teorema Tellegen statueaza ca, pentru un circuit cu m = n - 1 ramuri, S_k v_k(t) i_k(t) = 0, adica suma produselor curentilor si ale tensiunilor din oricare ramura k este nula.

Reteaua adjuncta, artificiu utilizat în determinarea sensitivitatii

Metoda numerica de determinare a sensitivitatii iesirii, în raport cu elementele rezistive ale unui circuit, consta în analizarea a doua circuite: reteaua originala N si reteaua adjuncta N^*.

O prima aproximare este exprimata prin faptul ca tensiunea de iesire V₀ în reteaua originala este masurata la nodurile unei surse de curent i₀ = 0 (introducerea acestei surse de curent nu afecteaza comportamentul circuitului, ci doar furnizeaza o ramura de masurare a iesirii).

Reteaua adjuncta, ca topologie, este o retea identica retelei originale pentru care în iesire se introduce o sursa de curent f

reteaua originala reteaua adjuncta

i_i N I₀ =0 f_i N^* f

Figura 11. Similiraritatea circuitului original si adjunct

Notam:

i_k , v_k - curenti si tensiuni în reteaua originala si, respectiv,

f_k n_k - curenti si tensiuni în reteaua adjuncta.

Deoarece cele 2 retele - reteaua originala si adjuncta - au aceeasi topologie se poate aplica teorema Tellegen pentru elementele oricarei ramuri k ale celor 2 circuite [23], [24], [25], [26] si se poate scrie:

S v_k f_k

S i_k n_k

Scopul acestui algoritm este de a cunoaste masura în care variatia elementelor unui circuit DR_k afecteaza iesirea V_o.

Dv_k = DR_k i_k + R_k Di_k (28)

unde k = 1,2 ... n, stiind ca Di₀ = 0 si Di_i = 0 (intrarea si iesirea nu sunt perturbate).

Deoarece cele 2 circuite, reteaua originala si adjuncta, au aceeasi topologie, cu toata perturbatia, se poate aplica teorema Tellegen între elementele oricarei ramuri k ale celor 2 circuite, si

S_k (v_k + Dv_k )f_k S_k (v_k f_k Dv_k f_k) = 0 S_k Dv_k f_k = 0

S_k (i_k +Di_k )n_k S_k (i_k n_k Di_k n_k) = 0 S_k Di_k n_k

Daca scadem relatiile de mai sus si înlocuim Dv_k, obtinem (de asemenea = 0).

S_k Dv_k f_k - S_k Di_k n_k S_k DR_k i_k + R_k Di_k) f_k - S_k Di_k n_k

S_k [(R_kf_k n_k Di_k + i_k f_kDR_k] = 0 unde R_kf_k n_k

Aplicând din nou teorema Tellegen si tinînd cont si de intrari si iesiri, relatia de mai sus devine:

Dv_i f_i Dv₀ f + S_k i_k f_kDR_k = 0, unde f_i 0 iar f 1 (conform definitiei circuitului adjunct) ==> Dv₀ + S_k i_k f_kDR_k = 0.

Cum sensitivitatea este expresia schimbarilor asupra iesirii DV₀ datorate schimbarilor (perturbarilor) elementelor R_k, se demonstreaza ca sensitivitatea iesirii este:

Nenormalizata  = DVo /DR_k = - i_kf_k

normalizata  = () DVo /DR_k = - (R_k/Vo) i_kf_k (30a)

Adica, sensitivitatea iesirii în raport cu perturbatiile elementelor R_k, se defineste ca fiind negativul produsului curentilor în ramura k din reteaua originala si adjuncta [27], [28], [29].

2.1.7. Algoritmi PAC pentru optimizarea proiectarii circuitelor electronice

Obiectivul PAC este formalizarea unui rationament calitativ al circuitelor, cum ar fi determinarea marimilor care permit optimizarea circuitului, studiind influenta ajustarilor elementelor cu scopul de a minimiza functia de performanta.

Se defineste functia de performanta e ca fiind o masura numerica a comportamentului circuitului, reprezentând eroarea între raspunsul real si cel dorit [5], [9] si se defineste:

e S _k | V₀ (jw_k) - V^'₀ (jw_k)| ² , unde k = 1,2, ... n (30)

unde:

V₀ - valoarea tensiunii de iesire reale;

- valoarea tensiunii de iesire ideale (dorite);

k - numarul punctelor din intervalul de frecventa, în urma esantionarii intervalului respectiv;

w w w_{k ....} - puncte de frecventa din intervalul studiat.

Functia de performanta, de pe alta parte, este definita ca fiind e f (p₁, p₂, ...p_n), unde p₁, p₂, ...p_n reprezinta parametrii circuitului.

Notam cu p = (p₁, p₂, ...p_n), vectorul parametru, atunci e f (p) sau, prescurtat, e (p). Problema devine determinarea valorii cu care trebuie ajustat vectorul parametru p încât sa se minimizeze functia de performanta e f (p).

Consideram 2 pasi, i +1 si i , în variatia valorilor vectorului parametru.

Notam D p = p ⁱ⁺¹ - p ⁱ , schimbarea vectorului p între pasii i +1 si i.

În acest caz, e (p ^{i +1} ), în urma expandarii în serie Taylor:

e (p ⁱ + D p ⁱ ) = e (p ⁱ ) + e (p ⁱ ) D p ⁱ , unde e (p ⁱ ) = = (de dp₁, de dp₂ de dp_n) ⁱ

Aplicând definitia initiala a functiei de performanta e, se poate determina:

de dp_j = S _k W_k d dp_j (31)

unde indicele ^*reprezinta reteaua adjuncta [13], [15], [17].

2.1.7.1. Optimizarea circuitelor prin metoda gradientului functiei de performanta

Algoritmul de optimizare a unui circuit consta în urmatorii pasi:

se considera circuitul cu elemente initiale, fiind excitat de un semnal având o frecventa initiala si finala, numar puncte de frecventa pentru care se analizeaza circuitul;

se stabileste numarul de parametri ajustabili;

se determina reteaua adjuncta;

se determina tensiunea si curentii pentru reteaua adjuncta;

se calculeaza functia de performanta si gradientul acesteia, urmarindu-se minimizarea acestuia.

Pasii algoritmului de determinarea a functiei de performanta sunt:

se analizeaza reteaua originala si se determina curentii si tensiunile în ramuri Vr si Ir;

se construieste reteaua adjuncta [12], [13], [19], excitând iesirea cu o sursa unitara de curent, si se determina curentii si tensiunile în ramuri reteaua adjuncta Vr^* si Ir^*.

Aplicând teorema Tellegen si producând variatii în elementele circuitului original, se poate scrie:

(Vr + DVr) Ir^* - (Ir + DIr) Vr^* = 0

DVr Ir^* - DIr Vr^* = 0 (32)

S _r (DVr Ir^* - DIr Vr^* ) = 0

De aici, se poate determina influenta variatiei elementelor circuitului asupra functiei de performanta [15], [17] exprimata în relatiile de mai jos.

rezistenta  dV₀/dR = IrIr^*

capacitate  dV₀/dC = jwVcVc^* inductanta  dV₀/dL = -jwI_LI_L^*

BJT conductanta  dV₀/dg_m = Vg_mVg_m^*

2.1.7.2. Optimizarea circuitelor prin controlul idealizarilor

Se porneste de la observatia ca influenta elementelor parazite existente într-un circuit real poate fi controlata prin studierea evolutiei sensitivitatilor si a functiei de performanta. Se constata ca variatia sensitivitatilor, adica a deviatiilor fata de un circuit ideal, depinde de elementele pasive din circuit si de topologia acestuia.

Proiectarea unui circuit începe cu un studiu al circuitului ideal, în care elementele parazite sunt neglijate; dupa aceasta, este necesara resimularea proiectarii circuitului tinând cont de elementele parazite, cele doua comportamente fiind apoi comparate. Comportamentul parazit este studiat prin determinarea sensitivitatilor in raport cu elementele parazite nenule; un exemplu în acest sens, îl constituie impedantele de intrare si iesire ale circuitului care au valoare nenula

Metoda de proiectare propusa presupune minimizarea constrângerilor reprezentate de coeficientii functiei de transfer, ceea ce conduce la ideea determinarii sensitivitatilor functiei obiectiv [27], [28], [29].

Dupa determinarea unei solutii de proiectare acceptabile, ca topologie si ca valoare ale componentelor, este important de a se simula o proiectare realista, consistenta în care sa se tina seama de tolerantele parametrilor ce caracterizeaza componentele si insensibila la variatia acestora.

În acest sens, este posibil de a se optimiza proiectarea propriu zisa prin controlul idealizarilor care se realizeaza prin utilizarea informatiilor furnizate de:

analiza sensitivitatilor

variatia functiei de performanta

Presupunerea de la care se porneste se refera la:

existenta unui criteriu de performanta, în care sunt încorporate constrângerile raportate la parametrii proiectului, criteriu care reflecta bonitatea unei proiectari;

existenta unei proiectari de referinta, satisfacatoare în raport cu criteriu de performanta

Plecam de la un circuit ale carui functii de performanta este dependenta de vectorul parametru P; se noteaza cu e_i - deviatia reala a parametrilor raportata la scalarul J al functiei de performanta la iteratia i, p⁰ parametru conform proiectului nominal iar cu D_i - deviatia admisibila a functiei de performanta la iteratia i.

Pentru a determina limita optima a variatiei parametrilor pentru ca sa fie respectata valoarea admisibila a deviatiei functiei de performanta, se procedeaza astfel:

se analizeaza alura functiei de performanta la iteratiile date;

se determina punctele de intersectie între curba functiei de performanta, luând în considerare vectorul parametru P, si scalarul functiei performanta notata J_i D_i (deviatia admisibila a functiei de performanta la iteratia i), unde J_i corespunde iteratiei i [23], [24].

Punctele de intersectie, corespunzatoare parametrului p_k sunt numite schimbari de scala larga a sensitivitatii si sunt caracterizate de dependenta L_k (J, p⁰, D

Pentru rezolvarea concreta a problemelor de proiectare, este important plasarea valorilor nominale ale unui proiect în regiunea de acceptabilitate a deviatiei functiei de performanta. Determinarea sensitivitatilor si a conturului acestei functii indica proiectantului cum sa desensitivizeze, in sensul de scala larga, un proiect prin "centrarea" valorii nominale

Una din problemele cele mai dificile existente în procesul de proiectare, în sensul obtinerii unui circuit performant cu costuri scazute, o constituie determinarea tolerantelor componentelor în asa fel încât functia de performanta a circuitului proiectat sa ramâna în regiunea de acceptabilitate.

2.1.7.3. Modelul incremental pentru analiza sensitivitatilor

În cele ce urmeaza, se prezenta un model alternativ la modelul circuitei adjuncte pentru analiza sensitivitatilor, ceea ce reprezinta partea originala a cercetarilor [27], [28], [29].

Ideea construirii "modelului incremental" pentru analiza sensitivitatilor pleaca de la observatia ca distributia tensiunii si a curentului este în corespondenta cu variatia parametrilor din reteaua originala, ceea ce reduce cazul la analiza de semnal mic a unei circuite nelineare.

În cazul analizei sensitivitatilor utilizând modelul circuitului adjunct, asa cum a fost prezentat anterior, se construieste reteaua adjuncta N^* având aceeasi topologie cu reteaua originala si matricea impedanta Z egala cu Z^*. Acest artificiu conduce la o simplificare a algoritmilor de calcul a sensitivitatilor. Vom demonstra ca acelasi rezultat se obtine utilizând modelul "reteaua incrementala".

Asa cum se stie, sensitivitatile la variatia elementelor din ramurile circuitului pot fi obtinute utilizând relatiile:

S_p (I _p dV_p - V_pdI _p) = I_p²dZ_p = S_r I _rI _{r *}dZ _r (34)

S_p (V_p dI_p - I_pdV_p) = V_p²dY_p = S_r V_rV_r* dY_r

unde

Zp si Yp reprezinta impedantele respectiv admitantele portului,

Z r si Yr reprezinta matricea impedantelor respectiv admitantelor.

Considerând sursele de excitatie de valoare 1 si 0, V0 = 1 pentru p ≠ r si V0 = 0 pentru p = r, deci dVr = 0, atunci

dIp = - Sr I rI r* dZ r r* si dZp = Sr I rI r* dZ r r*.

Aplicând teorema Tellegen, se obtin relatiile :

S_p (I _p dV_p - V_pdI _p) = I_p²dZ_p = S_r [I _rI _r* dZ _r + (I _rdI _r* - I _r*dI _r) Z _{r r*})]

S_p (V_p dI_p - I_pdV_p) = V_p²dY_p = S_r [V_rV_r* dY_r + (V _rdV _r* - V _r*dV _r) Y _{r r*}]

Se observa ca sensitivitatile sunt exprimate în functie de variatia valorilor elementelor de ramura si a valorilor tensiunilor si curentilor din ramura.

O abordare alternativa pentru determinarea sensitivitatilor o constituie "construirea" unui circuit incremental ∆N în locul circuitului adjunct. Reteaua incrementala, care este o generalizare a modelului utilizat în analiza de semnal mic, are o topologie identica cu a retelei originale N si o distributie de curenti si tensiuni corespunzatoare celor din reteaua originala; similar, se prezinta si incrementarile acestora. Elementele celor doua circuite N si ∆N sunt identice; pentru fiecare impedanta de ramura se considera ca exista o sursa de tensiune, de valoare egala cu "caderea de tensiune" corespunzatoare, la un curent constant, a valorii incrementate a impedantei, si în serie, cu fiecare sursa de curent controlata; relatiile duale se aplica admitantelor de ramura si surselor de curent controlate (în problemele de sinteza a circuitelor, parametrul variabil este frecventa).

În continuare, este prezentat modul de construire a modelului incremental, corespunzator circuitului original:

I₁ Y₂ I₂

V₁ Y₁ Y_mV₁ Y₃ V₂

Figura 14(a). Modelul de semnal mic a unui tranzistor (reteaua originala)

(V₁-V₂)dY₂

dI₁ Y₃ dI₂

V₂dY₃

dV₁ Y₁ V₁dY₁ V₁dY_m dV₂

I₁ Y_m dV₁

Figura 14(b). Modelul incremental a circuitului de mai sus

Luând ca parametru variabil frecventa, la capacitatea C si tensiunea V_c din reteaua N vor corespunde, în reteaua ∆N, capacitatea C si o sursa de curent de scurtcircuit jVdω; similar, daca parametrul variabil este temperatura T, respectiv, capacitatea C = C (T), atunci elementele corespondente în reteaua ∆N sunt capacitatea C si o sursa de curent de scurtcircuit jωVdC.

În problemele de optimizare a sintezei unui circuit, modelul incremental de prim ordin produce variatii ale frecventei tensiunii si ale curentului de iesire DV₀ si DI₀; modelul incremental de ordinul doi, în raport cu un element selectat din ramura, produce variatii ale tensiunii si ale curentului de iesire DV₀ si DI₀ corespunzatoare cu valoarea elementului din ramura, relevând existenta unei valori minime, daca aceasta exista. În afara de relatiile incrementale între curentii si tensiunile din circuitele N si DN, pot fi derivate incrementari ale impedantelor porturilor (se considera o retea cu un singur port cu impedanta Z_P respectiv Z^*_P).

Un alt exemplu de model incremental, derivat dintr-o retea originala, pentru care se presupune ca variaza toate elementele este:

Z₁ Z₃ - Z_m I₁ +

V₁ I₁ Z₂   I₂ V₂

Figura 15(a). Reteaua originala - punte de impedante

Z₁ I₁dZ₁  Z₃ Z_m I₁ I₂dZ₃ Z_mdI₁

I₁dZ_m + -- - + - + - +

Z₂

dI₁ dI₂

dV_{1 +} (I₁+I₂) dZ₂

dV₂

Figura 15(b). Modelul incremental aferent, în care elementele de circuit sunt înlocuite cu modelele lor incrementale

Un alt exemplu este prezentat în figura 16.

a) + b) B C

V_I

Y_b g_mV_be

Y_IN

Y_L

E

Figura 16(a) - Amplificator Darling Figura 16(b) - Modelul de frecventa joasa

V_i Y_b1 g_m1 V₂^*

V₂^*

g_m2 V₃^*

Y_b2 V₂ g_m1 (V₂ - V₃) Y_b1

Y_IN  Y_b2

V₃ V₁^* V₃^*

g_m2 (V₂ - V₃)

Y_L Y_L

Figura 16(c) circuitul echivalent Figura 16(d) reteaua adjuncta

Y_IN = Y_b1 Y_b2 Y_L / (Y_b1 + g_m1)( Y_b1 + Y_L + g_m2) + Y_b2 Y_L

Matricea admitanta a circuitului echivalent este:

Y_b1 -Y_{b1 0}

- (Y_b1 + g_m1) (Y_b1 +Y_b2 + g_m1) Y_b2 (36)

0 - (Y_b2 + g_m2) (Y_b2 + g_m2+ Y_L)

În acest caz, sensitivitatea sau dY poate fi scrisa ca:

dY = (V₁^*V₁)^-1 [V₂^*V₁ dY₂₁ + V₂^*V₂ dY₂₂ + V₃^*V₂ dY₃₂ + V₃^*V₃ dY₃₃].

Deoarece -dY₂₁ = dY₂₂ = dg_m1 si -dY₃₂ = dY₃₃ = dg_m2

Atunci dY = (V₁^*V₁)^-1 [V₂^*( V₂ - V₁) dg_m1 + V₃^*(V₃ - V₂) dg_m2]

Notând cu Δ = (Y_b1 + g_m1) (Y_b2 + g_m2+ Y_L) + Y_b2 Y_L

V₂ / V₁ = (Y_b1 + g_m1) (Y_b2 + g_m2+ Y_L) / Δ

V₂^* / V₁ = Y_b1 (Y_b2 + g_m2+ Y_L) / Δ

V₃ / V₁ = (Y_b1 + g_m1) (Y_b2 + g_m2) / Δ

V₃^* / V₁ = Y_b1Y_b2 / Δ

dY = - Yb1Yb2 YL (Δ2)-1 [(Yb2 + gm2+ YL) dgm1 + (Yb1 + gm1) dgm2]

(37)

(e) - Modelul incremental pentru acest amplificator devine

dV₁ Y_b1 dV₂

Y_b2

g_m1(dV₁ - dV₂) (V₁ - V₂) dg_m1

dV₃

Y_L (V₃ - V₂) dg_m2

g_m2 (dV₃ - dV₂)

dY = (V₁²)^-1[V₂ V₁ dY₂₁+ V₂² dY₂₂+ V₂ V₃ dY₃₂+ V₃² dY₃₃+

(V₂ dV₁- V₁ dV₂)( Y₂₁-Y₁₂) + (V₃ dV₂- V₂ dV₃)( Y₃₂ -Y₂₃)

= (V₁²)^-1[V₂ (V₂ - V₁) dg_m1 + V₃ (V₃ - V₂) dg_m2 -

(V₂ dV₁- V₁ dV₂) g_m1 - (V₃ dV₂ - V₂ dV₃) g_m2]

Substituind V₂ / V₁ , V₃ / V₁ si

dV₁ = dV₂ = (Y_b1Y_b2 Y_L)^-1 [(V₁-V₂) Y_b1 (Y_b2 + g_m2+ Y_L) dg_m1 + (V₂-V₃) Y_b1 Y_b2 dg_m2]

dV₃ = (Y_b1Y_b2 Y_L)^-1 [(V₁-V₂) Y_b1 (Y_b2 + g_m2) dg_m1 + (V₂-V₃) Y_b1 Y_b2 dg_m2]

se obtine

dY = - Yb1Yb2 YL (Δ2)-1 [(Yb2 + gm2+ YL) dgm1 + (Yb1 + gm1) dgm2]

(38)

adica, o relatie similara cu relatia (37).

Se observa ca cele 2 abordari, metoda circuitului adjunct si a circuitului incremental, sunt similare, deoarece conduc la acelasi rezultat.

Pentru a sublinia ca cele 2 abordari sunt similare, o exemplificare în acest sens este relevanta. Se ia în considerare functia de performanta (eroare) definita ca e = j_w| V₂ - | ² dw, unde V₂ si sunt tensiunile de iesire reale si ideale în domeniu w de frecventa. Analiza unui circuit un singur etaj ce contine un tranzistor emitor comun în serie cu o reactie R_eC_e, conduce la urmatorul rezultat:

daca se utilizeaza abordarea circuitului adjunct, minimum lui e în raport cu C_e este dat de marimea gradientului de dC_e;

daca se utilizeaza abordarea modelului incremental în raport cu variatia de frecventa, minimum lui e în raport cu C_e este dat de marimea dY/(Δ²).

2.1.7.4. Utilizarea sensitivitatilor pentru determinarea optimului tolerantelor in domeniu timpului

Cercetarea actuala propune o metoda de determinare si de analiza a efectelor parazite ale elementelor circuitului asupra comportamentului acestuia în domeniu timp, astfel încât pentru o topologie data, sa se determine tolerantele care produc efecte minime si costuri reduse.

Ca rezultat al cercetarii, se urmareste gasirea unei metode de determinare a polilor sensitivitatii, care sa produca valoarea cea mai mica pentru Si (cazul ideal), deci si pentru Sr (cazul real), metoda ce presupune compararea sumei patratelor sensitivitatilor corespunzatoare iesirilor, notate Si, si sumei patratelor sensitivitatilor corespunzatoare iesirilor, tinând seama de variatia parametrilor, notate Sr.

Determinarea valorii Si se face prin construirea matricei determinate unic din functia de transfer si parametrii de timp si a vectorului corespunzator polilor si a zerourilor sensitivitatilor; determinarea valorii Sr se face prin corectarea valorii Si cu vectorul erorilor relative ale parametrilor circuitului. Se analizeaza raspunsul circuitelor la impulsul treapta. Analiza rezultatelor obtinute este folosita la determinarea tolerantelor optime, care produc cel mai ieftin circuit.

Definirea marimilor Si si Sr sunt:

(39)

unde

k_n = k(t_n) reprezinta n esantioane la un intervalul dat ale raspunsului k(t_n) în domeniu timp la semnalul impuls;

dk_n reprezinta eroarea raspunsului k_n datorita variatiilor parametrilor retelei.

Sensitivitatea se poate rescrie ca vector al polilor si zerourilor functiei de transfer atât pentru reteaua originala, cât si pentru reteaua adjuncta, astfel:

= Re(tb_i e^at+ e^at ) = c(t)y pentru i =1, 2, .n (40)

a_{i ,} b_i reprezinta polii respectiv zerourile functiei de transfer

unde:

y =^t (41)

f = [.]

h = [.]

iar f, h reprezinta vectorii complex conjugati, y^t = vectorul transpus.

(42)

p_i = tb_i e^at , q_{i =} e^at

atunci ² = y*N*Ny (43)

unde N - matricea parametrilor dependenti de timp, la momentul t₀ si polii si zerourile functiei de transfer. Cu indicele ^* sunt notati parametrii circuitului adjunct.

Cum matricea [N*N] este determinata unic din functia de transfer si parametrul t₀, rezulta ca numai vectorul y este dependent de topologia circuitului; deci calcularea lui SS cere numai calcularea vectorului y pentru reteaua originala si reteaua adjuncta.

Limita minima pentru Si

Conform relatiei (43), Si se mai poate scrie:

Si = Mz, unde   (44)

z = [.]^t , este similara matricei z pentru reteaua adjuncta.

si M = LU , conform relatiilor (3)-(6), echivalenta matricei rare a circuitului având separate partea reala si cea imaginara, unde coeficientii acesteia sunt:

M₁₁= M₂₂ = . M_n-1,n-1 = ℓ

M₁₂= = . = u₁ + ju₂ (45 )

M₁₃= = = = . = ℓ₁ + jℓ₂

M_nn = ℓ^*

Atunci Si devine:

Si = 2(ℓ + u₁) + 2(r - u₁) + 4u₁m₁m₂ + 4l₁m₁ +4ℓ₂m₁m₂ + ℓ^*  (46)

În continuare, sunt prezentate rezultatele cercetarii pentru determinarea limitei inferioare pentru sensitivitate, exprimate într-o metoda de obtinere a circuitului echivalent, corespunzator polului sensitivitatii în raport cu câstigul produs de un element activ, în asa fel încât sa produca scaderea efectelor parazite.

Metoda consta în:

exprimarea sensitivitatii ca functie de doi coeficienti m₁ = Re[] si m₂ = Im[], adica = m₁+ jm₂

determinarea valorilor pentru m₁ si m₂ în regiunea polului sensitivitatii, care produce limita inferioara pentru sensitivitate, deci corectiile corespunzatoare valorilor elementelor circuitului.

Determinarea marimii Sr

La determinarea analitica a marimii Sr se tine cont de vectorul eroarea relativa a parametrilor t unde elementele t_i reprezinta eroarea relativa a parametrilor x_i ai circuitei, anume t_i = dx_i /x_i.

Conform relatiilor (44) si (47), (dk_n)² = t^tS_n t , unde S_n = .

Conform relatiei = (47)

Cum S_n,ij = S_n,ji , Sr = S_n (dk_n)² = t^t S_n S_n t t^t SSt (48)

Determinarea tolerantelor optime

Determinarea marimilor Si si Sr foloseste la stabilirea optimului pentru tolerantele elementelor circuitului, deci a costului acestuia.

Notând cu g vectorul toleranta elementelor circuitului, costul C_i(g_i) se demonstreaza ca poate fi aproximat cu C_i = 1/, iar costul total al circuitului este C = S_nC_i

Tolerantele optime se obtin pentru cazul g_{i = |} t _{i |} (49)

2.2. Reprezentarea in forma grafica

Algoritmii de Proiectare Asistata de Calculator, descrisi anterior, realizeaza modelarea si simularea proiectarii circuitelor electronice. Pentru realizarea acestui scop, este nevoie ca datele de intrare sa fie furnizate într-un format adecvat calculului numeric si de a afisa datele de iesire (rezultatele) în asa fel încât sa fie interpretate cu usurinta de proiectant. Cea mai intuitiva si interactiva forma de reprezentare a datelor este reprezentare grafica.

Program de Sistem Unitate afisare

aplicatie grafic utilizator

Aplicatia

Structuri de date

Figura 17. Reprezentarea grafica

Se face distinctie între functiile de modelare si vizualizare (grafica interactiva). Pentru vizualizare, programele de aplicatii comunica un set de functii pentru afisarea si manipularea datelor grafice, independente de aplicatie si transmise unui "nucleu" de functii grafice.

Evolutia reprezentarilor grafice s-a deplasat spre standardizarea acesteia. Astfel, standardul PHIGS realizeaza definirea, afisarea si modificarea datelor grafice în 2D. În baza de date centrala, datele grafice sunt organizate ca structuri; functiile de selectare a atributelor devin elemente ale structurii, valorile atributelor din operatia de afisare fiind determinate în timpul traversarii structurii. Noul standard grafic MOTIF, dezvoltat de Open Systems Foundation, se bazeaza pe lucrul în ferestre multiple, ce pot fi repozitionate si pot avea dimensiuni variabile, pe meniu de tip "pop-up" si lucrul pe butoane si selectori. Se pot realiza interfete foarte prietenoase.

Reprezentarea în forma grafica a intrarilor consta în vizualizarea de catre proiectant a:

topologia circuitului (functii standard de reprezentare, modificare a elementelor de circuit, definirea topologiei, numerotarea nodurilor, a ramurilor si buclelor);

optiunile de analiza-simulare (descrierea parametrilor analizelor si vizualizarea semnalelor de intrare).

Faza de executie propriu - zisa consta în interpretarea de catre sistemul de calcul, a circuitului topologiei astfel definite, de construire a circuitelor echivalente si realizare a analizelor circuitului.

Reprezentarea în forma grafica rezultatelor consta în:

interpretarea de catre sistem a rezultatelor tabelare, obtinute în urma simularii si reprezentarea acestora în forma grafica, cum ar fi curbele de transfer în curent continuu si curent alternativ, precum si comportamentul în domeniu timp;

vizualizarea de catre proiectant a curbelor de iesire cu posibilitati de interpretare a curbelor, de comparare a diferitelor curbe de iesire, masurare a marimii functiei de iesire; un caz special este la reprezentarea curbei de transfer în curent alternativ, pentru care se pot vizualiza atât magnitudinea, cât si faza; datorita plajei mari în domeniu frecventei 1oHz - 100 Mhz, este necesara reprezentarea logaritmica.

3. Modelul Programatorului

Baza de date PAC

Înca din anii '80, a fost recunoscuta necesitatea integrarii datelor în sisteme PAC. Astfel, datele de natura grafica si negrafica pot fi stocate utilizând o descriere relationala a lor în functie de structura si tipul informatiei ce trebuie stocate, de manipularile care trebuie efectuate asupra structurii, de interfata bazei de date cu utilizatorul.

Existenta unui control central asupra datelor prezinta urmatoarele avantaje: eliminarea redundantelor, a inconsistentelor, posibilitatea de exploatare simultana, asigurarea integritatii si a securitatii datelor. Entitatile si reprezentarile grafice sunt modelate ca fapte_despre_obiecte si relatii_dintre_obiecte. Pentru reprezentarea, formala s-au introdus urmatoarele concepte:

entitate - o marime ce poate fi descrisa de proprietati (relatii);

proprietate (relatie) - o asociatie dintre entitati sau entitati-atribute;

atribut - reprezinta orice caracteristica la care poate fi asignata o valoare;

valoarea este o stare a unui atribut.

Modelul de interconectare este prezentat mai jos:

Controlor Vedere

Model

Figura 18. Modelul programatorului

Modelarea acestei structuri abstracte se poate face cu 3 modele fundamentale: ierarhice, în retea, relationale.

Problemele care se pun în fata procesului de modelare sunt: posibilitatea de determinare a modelului adecvat, modalitatile de manipulare a structurilor, necesitatea asocierii de atribute entitatilor si relatiilor, modul de organizare a bazelor de date PAC pentru a fi eficiente. Astfel, analiza critica asupra implementarilor modelelor în retea si relationale au demonstrat ca au la baza algoritmi sofisticati pentru a realiza operatii simple, ceea ce a condus la concluzia ca aceste modele nu sunt adecvate.

Exista 2 tipuri de persoane implicate în sistemele PAC: programatorul aplicatiei si inginerul proiectant (utilizatorul).

Programatorul aplicatiei este o persoana cu abilitati de abstractizare, familiarizat cu aparatul matematic si cu manipulari ale structurilor de date complexe; interesul acestuia este concentrat, în special, asupra procesarii algoritmice a datelor, fapt ce reprezinta procese complicate.

Inginerul proiectant este implicat într-un proces creativ si are tendinta de a interoga baza de date, uneori cu întrebari neobisnuite. Acesta cere aplicarea unor functii complexe, care necesita un acces rapid la un numar mare de articole interconectate. În procesul de proiectare, sunt implicate persoane cu abilitati diferite, fiecare grup fiind interesat în informatia relevanta pentru activitatea lui. Oricare dintre utilizatori trebuie sa aiba acces la baza de date, pentru a putea sa-si defineasca propria structura de date, eliminând din vizualizare datele inutile.

Deci, în principal, schema bazei de date trebuie sa cuprinda tipul datelor si relatiile dintre acestea, fiind capabila sa gestioneze versiuni multiple ale datelor si configuratii multiple pentru combinarea datelor. De asemenea, baza de date trebuie sa contina protocoale de verificare a consistentei datelor în vederea asigurarii tehnicilor de acces concurential.

Cerintele bazelor de date în PAC constau în definirea entitatilor si a relatiilor dintre entitati ("mai multe la mai multe"), modelarea structurii în termenii unui model de date, definirea operatiilor ce se efectueaza pe aceasta structura, definirea algoritmilor rezultanti care trebuie sa fie destul de simpli, definirea tipurilor de utilizatori potentiali, frecventa operatiilor în baza de date, flexibilitate marita fata de cea fixata de structurile ierarhice, cu posibilitatea de procesare din orice nod, si nu neaparat din radacina, si de la frunze spre radacina, posibilitatea de modelare si de procesare a structurilor omogene si recursive, traversarea de la un nivel la altul printr-un numar arbitrar de niveluri intermediare, independenta logica a datelor, ascunderea pentru utilizator a cailor de acces.

În dorinta de a se raspunde la aceste probleme, au fost abordate 2 directii distincte:

încorporarea mecanismelor de inteligenta artificiala (baza de cunostinte) prin dezvoltarea modelului relational ceea ce asigura controlul asupra procesului de proiectare;

structuri de date orientate obiect ca un model natural, apropiat abordarii existente în activitatea proiectantilor; desi nefundamentate teoretic la acelasi nivel cu celelalte modele ale schemelor de date, aceasta directie este cea mai promitatoare la momentul actual; sistemul de gestionare a datelor cuprinde functii referitoare la administrarea datelor, la interogarea si manipularea acestora.

utilizator schema de comunicatie

reprezentare interna

procesor de subschema de date

comunicatie mesaje intrare/iesire

subschema de procesor de prezentare

comenzi interne rezultate

program PAC subschema de reprezentare

a starii interne a procesului

subschema de sistem Baza de Date reprezentarea starii

comenzi a procesului în

Bazei de Date Baza de Date

Figura 19. Schema de Modelare PAC

Interfete pentru sistemele de Proiectare Asistata de Calculator

Sistemele PAC se caracterizeaza printr-un numar mare de componente (hard si soft) care trebuie sa-si comunice date. Componentele hard contin diferite procesoare, unitati de stocare a informatiei, dispozitive intrare/iesire alfanumerice de adresare.

Componentele soft din PAC contin module ce proceseaza si stocheaza date, asigurând comunicatia între sistem si utilizator

Interfata între 2 componente reprezinta utilizarea resurselor comune în concordanta cu una sau mai multe scheme de acorduri. Nu este necesar ca aceste 2 componente sa utilizeze aceeasi schema; resursele interfetei putând furniza o schema de transformare, care permite fiecarei componente sa utilizeze scheme diferite pentru a reprezenta aceeasi informatie.

Programele PAC, care efectueaza analiza si subschemele de transformare, opereaza asupra unei reprezentari interne a starii procesului, utilizând resursele în concordanta cu o anumita subschema. Regulile de transformare a schemei în reprezentarea interna a bazei de date sunt definite în limbajul de manipulare a datelor.

Transformarile datelor reprezentând starea procesului sunt realizate de un procesor de prezentarea rezultatelor specifice diferitelor dispozitive de iesire.

Comunicatia dintre utilizatori si sistemul PAC se realizeaza prin intermediul unui procesor de comunicatie, având scopul de a construi sau modifica reprezentarea interna a starii si de a interoga despre starea actuala a modelului.

4. Implementarea algoritmilor PAC

Algoritmii descrisi în partea I, au fost implementati în pachetul de programe Sanra, cu ajutorul caruia se realizeaza simularea functionarii circuitelor nelineare.

Algoritmii PAC pentru analizele unui circuit nelinear se realizeaza astfel:

a.      Partea pregatitoare a simularii analizei, care se reia la fiecare tip de analiza,

esantionarea semnalului de intrare si a intervalului de analizat;

construirea matricei circuitului;

determinarea coeficientilor ecuatiilor nodale

rezolvarea ecuatiilor nodale prin tehnica matricelor rare (factorizare LU).

Dupa realizarea fazei pregatitoare (esantionarea semnalului de intrare si a intervalului de frecventa), se continua cu punctul b.

b.     PAC în simularea analizei propriu zise

analiza de curent alternativ consta în:

analiza de semnal mic - initializare [stabilirea numarului de iteratii si verificarea convergentei, calculul parametrilor modelului tranzistorului, calculul tensiunilor de iesire si estimarea tensiunilor pe jonctiunile tranzistorului, determinarea modului de operare al tranzistorului (normal, taiere, saturare), executia punctelor a.2 - a.4 pentru semnal mic

construirea circuitului adjunct;

determinarea raspunsului prin rezolvarea ecuatiilor nodale având coeficienti complecsi, dependenti de frecventa.

analiza în timp consta în:

preluarea elementelor de circuit, inclusiv a tensiunilor initiale, pasului de integrare, a perioadei de timp (început, final

se executa punctele a.2 - a.4 pentru conditiile initiale ale circuitului;

se construieste reteaua companion;

se realizeaza analiza pentru reteaua companion.

Exemplele prezentate mai jos sunt:

Analiza în curent alternativ a unui amplificator cu un etaj;

Analiza în curent alternativ pentru un filtru trece banda;

Analizele în curent continuu si în domeniu timp pentru un Trigger Schmitt.

Simularea analizei în curent alternativ a unui amplificator cu un etaj, utilizând algoritmii PAC

Coeficientii ecuatiilor nodale pentru un amplificator cu un singur etaj

Y(1,1)=-( 1./RB); Y(1,5)=1. ; CIN(1)=- (1./RB)* VI;

Y(2,1)=(1./RB)+(1./RX); Y(2,2)=-(1./RX); CIN(2)=(1./RB)*VI

Y(3,1)=-(1./RX) ; Y(3,2)=(1./RX)+(1./RPI)+JW*(CMU+CPI); Y(3,3)=-JW*CMU

Y(3,4)=-(1./RPI)-(JW*CPI)

Y(4,2)=GM-JW*CMU; Y(4,3)=(JW*CMU)+(1./R0)+(1./RL) ; Y(4,4)=-(1./R0)-GM

Y(5,2)=- (1./RPI)-(JW*CPI)- GM; Y(5,3)=-1./R0

Y(5,4)=GM+(1./RPI)+(1./RE)+(1./R0)+JW*CPI

Reprezentarea marimii de iesire - amplitudine VM(3,0) si faza VP(3,0) la temperatura de 27

Filtru trece banda - Analiza în curent alternativ. Reprezentarea marimii de iesire - amplitudine VM(7,0) si faza VP(7,0) la temperatura de 27°

Trigger Schmitt Analiza în curent continuu (DC) -V(5) / T= -15° Tensiunea de iesire (nodul 5) la temperatura de -15

Trigger Schmitt Analiza în domeniu timp - la temperatura de -15° Tensiunea în

punctul de intrare V(1) / T= -15°; Tensiunea de iesire - V(5) / T=-15°

Rezumatul partii I

Partea I cuprinde descrierea principalelor caracteristici si a problemelor specifice algoritmilor de Proiectare Asistata de Calculator a circuitelor electronice nelineare.

Pornind de la conceptele de baza privind analiza procesului de proiectare, se realizeaza modelarea obiectelor proiectarii într-o schema abstracta, definita ca arhitectura a sistemului de Proiectare Asistata de Calculator.

În capitolul 2, sunt descrise metodele de analiza numerica, de simulare si optimizare, urmarind pasii de executie:

determinarea coeficientilor ecuatiilor nodale din topologia circuitului, fara o numerotare prealabila a nodurilor circuitului, scrierea automata a ecuatiilor circuitului;

construirea matricei circuitului si rezolvarea ecuatiilor prin tehnica matricelor rare (factorizare LU), simularea functionarii în domeniul curentului alternativ utilizând artificiul - "reteaua adjuncta", în domeniul timp, utilizând artificiul "reteaua companion", determinarea sensitivitatilor utilizând artificiul "reteaua adjuncta" si analiza functionarii circuitului functie de conditiile exterioare (temperatura) si variatia valorilor elementelor circuitului.

Capitolul 3 cuprinde specificatiile tehnice - structuri de date, baza de date, dialogul tehnic si comunicarea om-calculator (transformari de vizualizare) - corespunzatoare modelului programatorului.

Capitolului 4 contine exemple de implementare a algoritmilor analize ale circuitelor în curent continuu, în domeniul frecventa si în timp.

Elementele de originalitate în simularea acestor analize îl constituie:

determinarea coeficientilor ecuatiilor nodale din topologia circuitului, fara o numerotare prealabila a nodurilor;

adaptarea si implementarea algoritmilor de proiectare asistata de calculator a circuitelor nelineare în realizarea analizelor de curent alternativ, în timp, în curent continuu;

algoritmi de proiectare asistata de calculator în controlul idealizarilor, si anume determinarea evolutiei sensitivitatilor utilizând modelul circuitului adjunct si modelul incremental;

elaborarea si implementarea algoritmilor de proiectare asistata de calculator în analiza evolutiei circuitului pentru mai multe temperaturi simultan.