Sistem informatic pentru asistarea deciziei bazat pe o baza de date
In cazul stabilirii unor decizii care pot fi rezolvate partial cu proceduri cunoscute, intrucat acestea au elemente predominant cantitative, scopurile nu sunt precise, iar procedura de rezolvare nu asigura ansamblul elementelor problemei, in conformitate cu terminologia lui H. Simon, in cazul acestor proceselor apare nevoia unui „asistent”, de fapt o „asistare a deciziei”. Acest termen de „asistare a deciziei” trebuie definit la modul general ca fiind o serie de operatii cum sunt sortarea, clasificarea, selectarea, evaluarea ce au ca scop final organizarea informatiei, reducerea incertitudinii si obtinerea de variante de rezolvare.
Daca se considera evolutia in timp a acestui termen, a aparut un alt nivel de abordare a asistarii deciziei, si anume „asistarea interactiva”. Pe baza acesteia au aparut sistemele informatice de asistare a deciziei sau Decision Support Systems (DSS).
Sistemelor Informatice pentru Asistatrea Deciziei (SIAD) se pot clasifica dupa mai multe criterii, cel mai des utilizat fiind gradul de analiza a datelor pe care se bazeaza solutia:
1. SIAD-uri care au la baza modele. Modelul cantitativ este sprijinit de o
interfata care faciliteaza utilizarea.
2. SIAD-uri bazate pe date care se refera la un volum apreciabil de date stocate in sistemul informatic al organizatiei si ofera posibilitatea de a extrage informatii utile din multitudinea de date de care dispune.
3. SIAD-uri bazate pe cunostinte care utilizeaza tehnologiile inteligentei artificiale si de aceea se mai numesc si SIIAD (sisteme informatice inteligente de asistare a deciziei).
SIAD care au la baza modele. Un SIAD foloseste un set de modele ca instrumente de analiza. Modelarea este considerata esentiala pentru sistemele informatice de asistare a deciziei si implica partea de concepere a problemei si partea de abstractizare in expresii cantitative sau calitative.
Modelul ofera un mod simplificat sau abstractizat de abordare a realitatii.
MODELAREA PROCESELOR DE ALOCARE A RESURSELOR[i]
Pentru modelarea proceselor de alocare a resurselor se pot utiliza mai multe tipuri de modele, dintre care amintim:
- modelul matematic de programare liniara;
- modelarea dinamica bazata pe principiul de optimalitate al lui Bellman;
- algoritmul euristic de alocare a resurselor ADC/RESURSE etc.
Matematica studiaza, ca orice stiinta, realitati obiective, oricat ar merge ea in domeniul abstractizarii. Abstractizarea este necesara pentru dezvoltarea matematicii ca stiinta, dar ceea ce reprezinta conditia necesara pentru dezvoltarea matematicii ca stare, nu se admite in cazul folosirii sale concrete. Deci ignorarea calitatii specifice a fenomenului nu poate duce decat la deformarea realitatii.
Matematicii ii revine sarcina sa constate daca alegerea variantei optime s-a facut cu procedee corespunzatoare, adica se poate verifica valabilitatea modului in care s-a obtinut rezultatul cantitativ necesar.
Prin urmare, cercetarea matematica se refera nu la aspectul pur matematic al problemei ci la continutul acesteia. Acest lucru arata ca rezultatele cercetarii utilizand a 343e44d paratul matematic in studierea diferitelor probleme din diverse domenii trebuie analizate prin prisma factorilor determinanti ai domeniului respectiv.
Rezulta ca aplicarea matematicii in diverse domenii trebuie sa fie bazata pe intelegerea esentei calitative a fenomenului, in functie de care sa se faca rezolvarea; numai astfel rezultatele matematice obtinute au un sens.
Modelul matematic de programare liniara este utilizat in reprezentarea unui proces economic si este constituit dintr-un ansamblu de ansamblu de ecuatii, inecuatii sau combinarea acestora, dintre care una reflecta obiectivul urmarit, iar celelalte cuprind restrictiile de resurse sau de tehnologie.
Denumirea de programare liniara deriva din aceea ca variabilele ce intra in componenta functiei obiectiv (scop) si a sistemului de conditii sunt de gradul intai.
Modelele de programare liniara sunt modele statice, ele nu surprind aspecte dinamice ale proceselor economice considerate, de aceea, este necesara postoptimizarea.
Postoptimizarea problemelor de programare liniara permite abordarea in timp a fenomenelor economice prin tratarea aspectelor legate de variatia parametrilor constanti atasati, si anume: resurse, costuri si tehnologii de fabricatie. Exista doua posibilitati de studiere a sensitivitatii solutiilor optimale, si anume reoptimizarea si parametrizarea.
Reoptimizarea - consta in recalcularea solutiei optimale a unei probleme de programare liniara, in cazul in care se modifica unele din conditiile initiale:
modificarea disponibilului de resurse;
modificarea costurilor de productie;
modificarea normelor de consum;
asimilarea unui nou produs.
Reoptimizarea unei probleme de programare liniara presupune parcurgerea urmatoarelor etape:
- verificarea optimalitatii solutiei in conditiile schimbarii datelor problemei;
- determinarea solutiei optime a problemei modificate, daca solutia problemei initiale nu mai este optima.
Parametrizarea - urmareste determinarea variantelor posibile de solutii optime in cazul cand unii dintre parametrii constanti ai modelului variaza, liniar sau neliniar, in functie de mai multi parametri dati:
- componentele vectorului resurse pot inregistra modificari fata de valoarea estimata datorita unor cauze interne sau externe procesului economic analizat;
- profitul unitar este influentat de variatia preturilor;
- variatia coeficientilor matricei A.
Rezolvarea problemelor de programare parametrica impune parcurgerea urmatoarelor etape:
- determinarea solutiei optime pentru o valoare a parametrilor;
- studiul sensibilitatii solutiei optime la variatiile parametrului care o caracterizeaza.
Din punct de vedere matematic scopul programarii liniare este rezolvarea problemelor in care se cauta extremul (maximul sau minimul) unei functii liniare de n variabile, de forma:
f=c1x1+c2x2+ ….. +cjxj+…. cnxn (1)
cu conditia ca cele n variabile xj, j=1,2,3,n, sa satisfaca un sistem de m inecuatii sau ecuatii de forma:
a11x1+a12x2+…..+a1jxj+…..+a1nxn![]() b1
b1
a21x1+a22x2+…..+a2jxj+…..+a2nxn![]() b2
b2
(2)
ai1x1+ai2x2+…..+a2ijxj+…..+ainxn=bi
am1x1+am2x2+…..+amjxj+…..+amnxn![]() bm
bm
Valorile necunoscutelor trebuie sa fie nenegative, adica xj![]() 0, j=1,2,3..,n.
0, j=1,2,3..,n.
Coeficientii aij, i=1,2,3..,m; j=1,2,3..,n ce apar in sistemul (2) sunt coeficienti constanti, planificati sau determinati in mod statistic.
Necunoscutele xj sunt marimi ce trebuiesc determinate, iar coeficientii bi, i=1,2,3..,m marimi constante date, determinate de conditiile specifice procesului ce se studiaza; ei sunt coeficientii de restrictie ai procesului analizat.
Problemele de programare liniara impun, in mod curent, variabilelor xj si conditia de nenegativitate, aceasta pentru motivul ca necunoscutele xj reprezinta marimi utilizate in mod efectiv in realizarea unui plan si ca atare nu pot lua valori negative.
Din exprimarea matematica se constata ca procesul ce se analizeaza este subordonat realizarii unui anumit scop, exprimat matematic prin forma functiei (1), numita functie obiectiv (scop). Coeficientii acestei functii sunt constante caracteristice cj, j=1,2,3..,n.
De regula, se cere realizarea unei activitati sa se faca in conditii optime, fapt care conduce la a determina valorile optime (maxime sau minime) ale functiei obiectiv (scop). Cand astfel de solutii optime ale problemei de programare liniara exista, atunci pentru executarea in conditii optime a activitatii respective se impune determinarea valorilor necunoscutelor xj.
Cand numarul de relatii m este egal cu numarul de necunoscute n si cu rangul r al matricei formate din coeficientii aij, atunci sistemul este compatibil determinat. In astfel de situatii nu mai are sens sa se puna problema determinarii valorii optime pentru functia obiectiv, aceasta avand o valoare unica bine determinata, corespunzatoare sistemului de solutii al ecuatiilor de conditii.
Cand numarul de relatii m<n, rangul r<n, precum si r![]() m sistemul de conditii
este compatibil, dar nedeterminat. In astfel de situatii se poate alege
din infinitatea de solutii numai a acelora care fac functia obiectiv
optima (maxima sau minima).
m sistemul de conditii
este compatibil, dar nedeterminat. In astfel de situatii se poate alege
din infinitatea de solutii numai a acelora care fac functia obiectiv
optima (maxima sau minima).
Este evident ca pentru fiecare din cele m restrictii este precizat unul si numai unul dintre
semnele ![]()
![]()
Daca se ia in sistemul (2) toate inecuatiile cu semnul ![]() , se pot obtine urmatoarele forme de
exprimare a unei probleme de programare liniara:
, se pot obtine urmatoarele forme de
exprimare a unei probleme de programare liniara:
a) Forma algebrica
Sa se determine valoarea maxima a functiei:
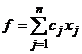 (3)
(3)
in conditiile:
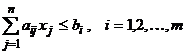 (4)
(4)
![]() (5)
(5)
Daca toate relatiile de conditii sunt ecuatii si tuturor variabilelor li se impun conditii de nenegativitate, forma problemei de programare liniara se numeste standard, si are forma:
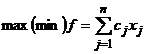 (6)
(6)
in conditiile:
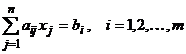 (7)
(7)
![]() (8)
(8)
Daca toate relatiile de conditii sunt inecuatii de acelasi sens si tuturor variabilelor li se impun conditii de nenegativitate, forma problemei de programare liniara se numeste canonica, si are forma:
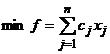 (9)
(9)
in conditiile:
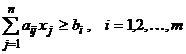 (10)
(10)
![]() (11)
(11)
sau
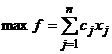 (12)
(12)
in conditiile:
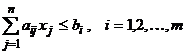 (13)
(13)
![]() (14)
(14)
b) Forma matriciala
Se vor considera matricele:
 ;
;
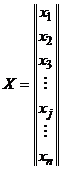 ;
; 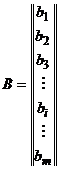
![]()
In acest caz problema programarii liniare se prezinta astfel:
![]() (15)
(15)
in conditiile:
![]() (16)
(16)
![]() (17)
(17)
din care rezulta urmatoarele forme:
Forma standard
![]() (18)
(18)
in conditiile:
![]() (19)
(19)
![]() (20)
(20)
Forma canonica
![]() (21)
(21)
in conditiile:
![]() (22)
(22)
![]() (23)
(23)
sau
![]() (24)
(24)
in conditiile:
![]() (25)
(25)
![]() (26)
(26)
c) Forma vectoriala
In matricea A se va nota cu ![]() , vectorii coloana ale caror componente
sunt elementele coloanelor matricei, iar cu
, vectorii coloana ale caror componente
sunt elementele coloanelor matricei, iar cu ![]() , vectorul determinat de matricea coloana B.
, vectorul determinat de matricea coloana B.
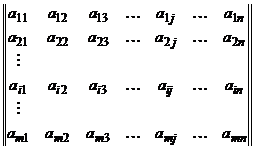
![]()
![]()
![]()
Vectorii ![]() , sunt numiti vectori de conditii, iar
vectorul
, sunt numiti vectori de conditii, iar
vectorul ![]() este numit
vectorul restrictiilor.
este numit
vectorul restrictiilor.
Daca se noteaza cu ![]() vectorul
format din vectorii
vectorul
format din vectorii ![]() , relatiile de conditii (25) si (26)
se vor scrie astfel:
, relatiile de conditii (25) si (26)
se vor scrie astfel:
![]() (27)
(27)
sau
![]() (28)
(28)
la care se adauga
conditiile de nenegativitate ale necunoscutelor ![]() , adica:
, adica:
![]() (29)
(29)
In acest caz problema de programare liniara se poate enunta astfel:
Sa se determine valorile optime ale functiei f date de (3) sau (15), astfel ca punctul ![]() sa
satisfaca ecuatia vectoriala (28) cu conditiile (29).
Rezulta urmatoarele forme:
sa
satisfaca ecuatia vectoriala (28) cu conditiile (29).
Rezulta urmatoarele forme:
Forma standard
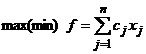 (30)
(30)
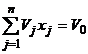 (31)
(31)
![]() (32)
(32)
Forma canonica
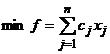 (33)
(33)
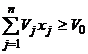 (34)
(34)
![]() (35)
(35)
sau
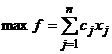 (36)
(36)
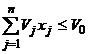 (37)
(37)
![]() (38)
(38)
Daca sensul inecuatiilor este ![]() functia obiectiv trebuie minimizata
iar daca inecuatiile sunt de forma
functia obiectiv trebuie minimizata
iar daca inecuatiile sunt de forma ![]() trebuie
maximizata.
trebuie
maximizata.
In aplicatiile practice apar frecvent situatii in care modelul contine simultan restrictii de toate tipurile. Restrictiile de forma ' ' sunt neconcordante pentru problemele la care se cere maximizarea functiei obiectiv, iar cele de tipul ' ' sunt neconcordante pentru problemele la care se cere minimizarea functiei obiectiv.
Orice problema de programare liniara se poate aduce la forma standard sau la forma canonica cu ajutorul unor transformari elementare efectuate asupra variabilelor sau (si) restrictiilor precum si a operatorului aplicat functiei obiectiv, astfel:
-
transformarea maximului in minim si invers se bazeaza pe
urmatoarea egalitate: ![]() , adevarata pentru orice multime X
si orice functie reala definita pe X; in particular
, adevarata pentru orice multime X
si orice functie reala definita pe X; in particular ![]()
-
transformarea sensului unei inegalitati se realizeaza prin
inmultirea cu ![]()
- o
variabila oarecare x (careia nu i se impune restrictie de semn)
se inlocuieste prin diferenta a doua variabile nenegative x=x1-x2,
![]()
![]()
- o
variabila ![]() se
inlocuieste cu o variabila nenegativa (–x);
se
inlocuieste cu o variabila nenegativa (–x);
-
transformarea inecuatiilor in ecuatii se realizeaza astfel: o
inecuatie ![]() poate fi
scrisa ca o ecuatie
poate fi
scrisa ca o ecuatie ![]() prin
introducerea variabilei
prin
introducerea variabilei ![]()
![]() , numita variabila auxiliara (de
compensare, ecart); o inecuatie de forma
, numita variabila auxiliara (de
compensare, ecart); o inecuatie de forma ![]() se poate
transforma in ecuatia
se poate
transforma in ecuatia ![]() prin
scaderea variabilei auxiliare (variabilele auxiliare nu apar in
functia obiectiv sau, astfel spus, apar cu coeficienti nuli);
prin
scaderea variabilei auxiliare (variabilele auxiliare nu apar in
functia obiectiv sau, astfel spus, apar cu coeficienti nuli);
-
transformarea ecuatiilor in inecuatii se realizeaza astfel: o
ecuatie ax=b este echivalenta cu urmatoarele doua
inecuatii de sens contrar ![]() si
si ![]()
Aceste transformari intervin in mod concret in rezolvarea problemelor de programare liniara. Astfel, metoda simplex (metoda iterativa de cercetare) este aplicabila numai problemelor exprimate sub forma standard.
Oricare ar fi domeniul de aplicare, programarea liniara consta in elaborarea si rezolvarea unor modele matematice care exprima atat aspectul cantitativ cat si cel calitativ al problemei. Trebuie retinut faptul ca modelul matematic nu se refera strict numai la aspectul matematic al problemei, ci mai ales la continutul acesteia.
In rezolvarea unei probleme de programare liniara, partea cea mai importanta (si dificila) o constituie elaborarea modelului matematic. Astfel, pornind de la datele problemei, acestea trebuie analizate si corelate pentru a exprima atat esenta cat si continutul problemei, descrise prin modelul matematic. Odata elaborat modelul matematic, solutionarea problemei este usor de realizat tinand seama de existenta metodelor, algoritmilor si a programelor de calcul.
Prin rezolvarea modelului matematic exista posibilitatea alegerii celei mai bune variante, a variantei optime de utilizare a unor resurse date, in conditiile existentei a numerosi parametrii si a unor restrictii impuse in rezolvare.
In solutionarea problemelor si obtinerea rezultatelor aplicand metodele programarii liniare, trebuie sa se tina seama de o serie de cerinte si anume:
- punerea problemei trebuie facuta in concordanta cu scopul urmarit, iar acesta trebuie formulat astfel incat solutia optima sa corespunda in ansamblul problemei deoarece este posibil ca varianta optima sa nu avantajeze toate unitatile carora li se vor repartiza resurse. Totusi acestea vor executa dispozitiile organului care a elaborat planul optim pentru toate unitatile si care va corespunde variantei optime in ansamblul actiunii;
- necesitatea ca datele problemei sa poata fi exprimate numeric (cantitativ). Nu este insa absolut necesar ca marimile ce produc limitari sa fie exprimate absolut precis, acestea pot sa aiba si forma inegalitatii, in sensul ca anumite masuri sa nu depaseasca o anumita valoare minima sau maxima;
- posibilitatea punerii sub forma ecuatiilor sau a inecuatiilor liniare corespunzatoare a datelor problemei, a conditiilor de restrictii si a legaturii dintre acestea si functia scop.
In problemele de programare liniara intervin doua elemente importante:
- multimea punctelor x, care reprezinta solutii ale relatiilor de conditii;
- multimea vectorilor ![]() , de componente
, de componente ![]()
![]() care
exprima proprietatile individuale ale relatiilor de
conditii.
care
exprima proprietatile individuale ale relatiilor de
conditii.
Asupra acestor elemente se pot face urmatoarele consideratii:
- un punct ![]() care
reprezinta o solutie a relatiilor de conditii, este un
punct al unui spatiu n
dimensional
care
reprezinta o solutie a relatiilor de conditii, este un
punct al unui spatiu n
dimensional ![]() , care se va numi spatiu al solutiilor.
Multimea punctelor x
determina in spatiul
, care se va numi spatiu al solutiilor.
Multimea punctelor x
determina in spatiul ![]() al
solutiilor o multime convexa, numita multimea solutiilor, iar in cazul cand formeaza un
poliedru, poliedrul solutiilor;
al
solutiilor o multime convexa, numita multimea solutiilor, iar in cazul cand formeaza un
poliedru, poliedrul solutiilor;
- vectorii ![]()
![]() , sunt definiti intr-un spatiu m dimensional
, sunt definiti intr-un spatiu m dimensional ![]() , denumit spatiul conditiilor. In acest spatiu vectorii
, denumit spatiul conditiilor. In acest spatiu vectorii ![]()
![]() , determina un poliedru convex, care se numeste
poliedrul conditiilor.
, determina un poliedru convex, care se numeste
poliedrul conditiilor.
Solutiile unei probleme de programare liniara pot fi:
- solutii
posibile - formate din orice sistem de valori ![]() care
satisfac, potrivit conditiilor, unul din sistemele de restrictii de
forma:
care
satisfac, potrivit conditiilor, unul din sistemele de restrictii de
forma:
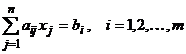
cu valori ![]()
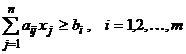 (39)
(39)
cu valori ![]()
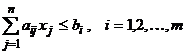
cu valori ![]()
- solutie de baza - in
care numarul necunoscutelor nenule ![]() este cel
mult egal cu numarul relatiilor ce exprima restrictiile (in
cazul unui sistem de restrictii din (39) numarul restrictiilor
este egal cu m); daca
solutia respectiva contine exact un numar de valori
este cel
mult egal cu numarul relatiilor ce exprima restrictiile (in
cazul unui sistem de restrictii din (39) numarul restrictiilor
este egal cu m); daca
solutia respectiva contine exact un numar de valori ![]() egal cu
numarul restrictiilor, atunci solutia se numeste solutie de baza nedegenerata;
daca solutia contine un numar de valori
egal cu
numarul restrictiilor, atunci solutia se numeste solutie de baza nedegenerata;
daca solutia contine un numar de valori ![]() mai mic
strict decat numarul restrictiilor, atunci solutia se
numeste solutie de baza degenerata;
mai mic
strict decat numarul restrictiilor, atunci solutia se
numeste solutie de baza degenerata;
- solutie optima (solutii optime) - solutia (solutiile) posibile care fac functia f din relatia (1) maxima sau minima, dupa cerintele problemei. O functie liniara f calculata pe o multime convexa isi atinge valoarea optima (maxima sau minima) cand aceasta exista intr-un punct extrem al multimii convexe considerate. Daca functia f ia valoarea optima in mai mult decat un punct al multimii convexe, atunci ea are aceeasi valoare pe toata multimea convexa generata de aceste puncte.
1.2. Problema transporturilor
Problema transporturilor rezolvata cu ajutorul programarii liniare are ca obiectiv fundamentarea deciziei privind transportul unor resurse materiale din depozite la beneficiari astfel incat pe ansamblu costul total al transporturilor sa fie minim.
In cadrul analizei problemelor de transport trebuie sa se aiba in vedere trei elemente esentiale si anume:
- functia scop (obiectiv) prin care se exprima matematic scopul urmarit prin rezolvarea (solutionarea) problemei;
- conditiile de restrictii care prezinta totalitatea restrictiilor sub forma unor ecuatii sau inecuatii liniare ce se impun in rezolvare;
- conditia de nenegativitate prin care se arata ca atat datele initiale cat si rezultatele partiale si finale ce se detin trebuie sa fie nenegative (
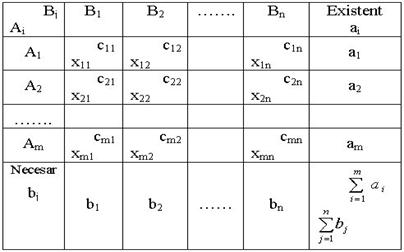
Modelul
matematic al unei probleme de transport, in cazul existentei a m depozite (centre) Ai, ![]() , in care se afla cantitatile ai,
, in care se afla cantitatile ai,
![]() si n beneficiari Bj,
si n beneficiari Bj, ![]() , fiecare avand nevoie de cantitatile bj,
, fiecare avand nevoie de cantitatile bj,
![]() , implica determinarea minimului unei
functii liniare de forma:
, implica determinarea minimului unei
functii liniare de forma:
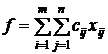 (40)
(40)
pe multimea solutiilor nenegative ale sistemului:
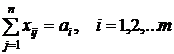
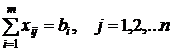 (41)
(41)
![]()
in care: ai>0; bj>0; ![]() ;
; 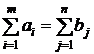 .
.
Valorile xij, ![]() ;
; ![]() reprezinta
cantitatile ce trebuiesc transportate de la depozitele Ai,
reprezinta
cantitatile ce trebuiesc transportate de la depozitele Ai,
![]() la beneficiarii Bj,
la beneficiarii Bj,
![]() , iar cij,
, iar cij, ![]() ,
, ![]() coeficientii
criteriului de eficacitate (km, cost, timp etc.) dintre depozitele Ai,
coeficientii
criteriului de eficacitate (km, cost, timp etc.) dintre depozitele Ai,
![]() si beneficiarii Bj,
si beneficiarii Bj,
![]() (tabelul 1).
(tabelul 1).
Tabelul 1
Orice problema de
transport cu 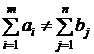 se poate aduce
la cazul in care exista egalitate intre existent si necesar.
se poate aduce
la cazul in care exista egalitate intre existent si necesar.
Deoarece 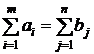 , sistemul de ecuatii (41) are un numar de m+n ecuatii liniare cu
, sistemul de ecuatii (41) are un numar de m+n ecuatii liniare cu ![]() necunoscute, din care
numai m+n-1 sunt ecuatii liniare
independente.
necunoscute, din care
numai m+n-1 sunt ecuatii liniare
independente.
Rezolvarea sistemului (41) pe cale algebrica este o operatie laborioasa, astfel ca se vor utiliza unele metode care sa conduca mai rapid la gasirea unei variante optime.
Solutionarea problemelor de transport imbraca urmatoarele aspecte:
- obtinerea unei solutii initiale de baza, aplicand una din metodele programarii liniare: nord-vest (repartitiei in scara); elementului minim pe linie; elementului minim pe coloana; elementului minim al matricei; diferentelor maxime; metoda ierarhizarii criteriilor (eficientelor);
- optimizarea solutiei initiale de baza utilizand metode ale programarii liniare de optimizare: metoda distributiva, metoda distributiv-modificata etc;
- obtinerea unei solutii finale si optime fara a porni de la o solutie initiala de baza: metoda acoperirii zerourilor, metoda diferentelor comparate etc;
- metode pentru solutionarea unor probleme speciale (particulare) de transport.
Metode pentru obtinerea unei solutii finale si optime fara a porni de la o solutie initiala de baza
Prin aplicarea metodelor din aceasta categorie se va obtine solutia finala si optima. Pentru domeniul militar se recomanda folosirea metodei acoperirii zerourilor, metoda care a fost elaborata de W. H. Kuhn si J. Egervary.
Aceasta metoda permite obtinerea unei solutii optime, fara a fi necesar sa se determine in prealabil o solutie initiala de baza.
Se cauta o prima solutie, in care, pornind de la matricea initiala se urmareste sa se obtina in fiecare linie si in fiecare coloana cel putin cate un zero.
Pentru aplicarea metodei trebuie ca existentul in surse ai
sa fie egal cu necesarul bj : 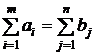
In practica se intalnesc deseori 2 (doua) cazuri: suma
existentului este mai mare decat suma necesarului, adica 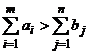 si suma existentului este mai mica decat
suma necesarului, adica
si suma existentului este mai mica decat
suma necesarului, adica 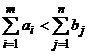
In cazul 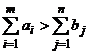 se
adauga la matricea cu datele initiale o coloana
suplimentara care va reprezenta un beneficiar fictiv. Coeficientii
criteriului de eficacitate vor avea valori nule.
se
adauga la matricea cu datele initiale o coloana
suplimentara care va reprezenta un beneficiar fictiv. Coeficientii
criteriului de eficacitate vor avea valori nule.
In solutia de rezolvare va rezulta ca si acestui beneficiar fictiv i se va repartiza o anumita cantitate de materiale, dar ea va ramane in mod real in sursa (nu se stie de la inceput in care va ramane) si a carei valoare este data de relatia:
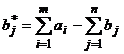
unde ![]() este necesarul beneficiarului fictiv.
este necesarul beneficiarului fictiv.
In cazul 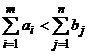 este necesara o cantitate mai mare de
materiale decat se dispune. In acest caz se adauga la matricea cu datele
initiale o linie suplimentara (o sursa suplimentara
fictiva) ai carei coeficienti de eficacitate au valori nule.
este necesara o cantitate mai mare de
materiale decat se dispune. In acest caz se adauga la matricea cu datele
initiale o linie suplimentara (o sursa suplimentara
fictiva) ai carei coeficienti de eficacitate au valori nule.
In solutia de rezolvare va rezulta ca unui beneficiar ii va fi repartizata o cantitate de materiale (din sursa fictiva A*i) a carei valoare este egala cu:
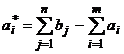
Algoritmul de aplicare al metodei consta in:
- obtinerea zerourilor pe linii
In matricea cu datele initiale se cauta sa se obtina pe fiecare linie cel putin cate un 0 (zero). Pentru aceasta, elementul de valoare minima din cadrul fiecarei linii se scade din celelalte elemente, inclusiv din el insusi.
- obtinerea de zerouri pe coloane
In coloanele in care nu sunt obtinute zerouri se scade elementul de valoare minima din fiecare element al coloanei respective.
Se obtine cate cel putin un zero pentru fiecare linie si coloana. Elementele din matricea obtinuta pot fi considerate ca date pentru trecerea la aflarea unei prime solutii a problemei. Este posibil ca uneori datele din matrice sa permita aflarea solutiei finale a problemei, a solutiei optime. Pentru a constata caracterul datelor furnizate de matrice se procedeaza la verificarea ei potrivit cerintelor algoritmului metodei acoperirii zerourilor.
- se verifica solutia din matricea obtinuta daca este optima
Se vor nota cu IK liniile ce se suprima (acopera), cu JK coloanele in care exista zerouri cand se suprima (acopera) liniile IK si cu SK sumele ce se efectueaza, Sk=aai+abj, unde ai si bj reprezinta existentul, respectiv necesarul corespunzator liniilor suprimate si coloanelor cu zerouri cand se suprima liniile, pentru fiecare situatie in parte.
Daca sunt un numar de m
linii (surse) atunci numarul de sume Sk ce trebuiesc calculate
va fi dat de relatia ![]()
- se verifica sumele SK obtinute
Daca SKmin ![]() . In cazul in care aceasta conditie este
indeplinita inceteaza
aplicarea metodei, urmand ca repartitia resurselor pe beneficiari sa
se faca in celulele corespunzatoare matricei initiale conform cu
pozitia si numarul zerourilor din matricea finala, astfel:
in matricea finala se pun necunoscutele
. In cazul in care aceasta conditie este
indeplinita inceteaza
aplicarea metodei, urmand ca repartitia resurselor pe beneficiari sa
se faca in celulele corespunzatoare matricei initiale conform cu
pozitia si numarul zerourilor din matricea finala, astfel:
in matricea finala se pun necunoscutele ![]() in locurile
ocupate cu zero si zero in locurile unde
in locurile
ocupate cu zero si zero in locurile unde ![]() este
diferit de zero; se completeaza coloanele in care este o singura
necunoscuta, repartizandu-se cantitatea necesara indicata de
este
diferit de zero; se completeaza coloanele in care este o singura
necunoscuta, repartizandu-se cantitatea necesara indicata de ![]() ; se completeaza liniile in care exista
o singura necunoscuta; se determina valorile celorlalte
necunoscute, tinand seama de cele deja determinate.
; se completeaza liniile in care exista
o singura necunoscuta; se determina valorile celorlalte
necunoscute, tinand seama de cele deja determinate.
In
cazul cand se obtine SKmin<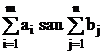 , inseamna ca solutia
obtinuta nu este optima, ceea ce impune recorectarea acesteia.
, inseamna ca solutia
obtinuta nu este optima, ceea ce impune recorectarea acesteia.
Recorectarea
presupune efectuarea urmatoarelor operatii: daca sunt mai multe
sume SK<![]() , atunci se alege suma cu valoarea cea mai
mica; se taie in ultima matrice liniile si coloanele care au dat SKmin;
se alege elementul minim din celulele netaiate, se scade din toate
elementele celulelor netaiate si se adauga la elementele
celulelor dublu taiate; elementele celulelor taiate o singura
data raman neschimbate. Se intocmeste o noua matrice pentru
care se calculeaza sumele SK dupa acelasi algoritm
si se reia algoritmul pana cand este indeplinita conditia
de incetare a aplicarii metodei SKmin
, atunci se alege suma cu valoarea cea mai
mica; se taie in ultima matrice liniile si coloanele care au dat SKmin;
se alege elementul minim din celulele netaiate, se scade din toate
elementele celulelor netaiate si se adauga la elementele
celulelor dublu taiate; elementele celulelor taiate o singura
data raman neschimbate. Se intocmeste o noua matrice pentru
care se calculeaza sumele SK dupa acelasi algoritm
si se reia algoritmul pana cand este indeplinita conditia
de incetare a aplicarii metodei SKmin ![]()
Se calculeaza functia obiectiv. Activitatea de transport planificata conform acestei solutii va fi optima.
Exemplu de calcul
Pentru
executarea unor aplicatii, cinci unitati notate ![]()
![]() se vor
aproviziona cu munitie de la trei depozite de teritoriu, notate cu
se vor
aproviziona cu munitie de la trei depozite de teritoriu, notate cu ![]()
![]() . Existentul in surse
. Existentul in surse ![]()
![]() (in tone)
notat cu
(in tone)
notat cu ![]()
![]() , necesarul unitatilor (in tone) notat
cu
, necesarul unitatilor (in tone) notat
cu ![]()
![]() si
distantele cij,
si
distantele cij, ![]()
![]() (in
kilometri) de la surse la unitati, se dau in tabelul 41.
(in
kilometri) de la surse la unitati, se dau in tabelul 41.
Tabelul 41
|
Bj Ai |
B1 |
B2 |
B3 |
B4 |
B5 |
ai |
|
A1 | ||||||
|
A2 | ||||||
|
A3 | ||||||
|
bj |
Se
cere sa se repartizeze unitatilor ![]() ,
, ![]() cantitatile
cantitatile ![]() ,
, ![]() de la sursele
de la sursele ![]() ,
, ![]() cu existentul
cu existentul ![]() ,
, ![]() , astfel incat activitatea totala de transport
masurata in
, astfel incat activitatea totala de transport
masurata in ![]() sa fie minima.
sa fie minima.
Algoritmul de aplicare al metodei:
- obtinerea zerourilor pe linii
In matricea cu datele initiale (tabelul 41) se cauta sa se obtina pe fiecare linie cel putin cate un 0 (zero). Pentru aceasta, elementul de valoare minima din cadrul fiecarei linii se scade din celelalte elemente, inclusiv din el insusi, obtinandu-se matricea prezentata in tabelul 42.
Tabelul 42
|
Bj Ai |
B1 |
B2 |
B3 |
B4 |
B5 |
ai |
|
A1 | ||||||
|
A2 | ||||||
|
A3 | ||||||
|
bj |
- obtinerea de zerouri pe coloane
In coloanele in care nu sunt obtinute zerouri se efectueaza aceeasi operatiune ca si pe linii. Rezultatele obtinute sunt date in matricea din tabelul 43.
Tabelul 43
|
Bj Ai |
B1 |
B2 |
B3 |
B4 |
B5 |
ai |
|
A1 | ||||||
|
A2 | ||||||
|
A3 | ||||||
|
bj |
S-a obtinut pentru fiecare linie si coloana cate un zero. Aceasta poate reprezenta o prima solutie a problemei. Este necesara verificarea optimalitatii solutiei data de matricea din tabelul 43.
- se verifica daca solutia este optima
Se vor marca cu IK liniile ce se suprima (acopera), cu JK coloanele in care exista zerouri cand se suprima (acopera) liniile IK si cu SK sumele ce se efectueaza.
Se calculeaza sumele Sk in care Sk=aai+abj - unde ai si bj reprezinta existentul, respectiv necesarul corespunzatoare liniilor suprimate si coloanelor cu zerouri cand se suprima liniile, pentru fiecare situatie in parte.
I2=2
I3=3
I4=1,2
I5=1,3
I6=2,3
I7=1,2,3

se verifica sumele SK
obtinute, in sensul de a vedea daca SKmin 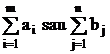 . In acest caz conditia SKmin
. In acest caz conditia SKmin 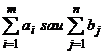 nu este indeplinita (S2=S4=34<40),
astfel ca se va face recorectarea
acesteia conform algoritmului enuntat. Se obtine matricea prezentata in tabelul 4
nu este indeplinita (S2=S4=34<40),
astfel ca se va face recorectarea
acesteia conform algoritmului enuntat. Se obtine matricea prezentata in tabelul 4
Tabelul 44
|
Bj Ai |
B1 |
B2 |
B3 |
B4 |
B5 |
ai |
|
A1 | ||||||
|
A2 | ||||||
|
A3 |
|
|||||
|
bj |
Se verifica daca solutia obtinuta este optima.
S2=16+40=56
S3=14+10+12+10=46
S4=10+16+4+4=34
S5=10+14+10+12=46
S6=10+14+10+12+10=62
S7=10+16+14=40
|
S1=10+4+10+12+4=40 S2=16+40=56 S3=14+10+12+10=46 S4=10+16+4+4=34 S5=10+14+10+12=46 S6=10+14+10+12+10=62 S7=10+16+14=40 |
|
I1=1 I2=2 I3=3 I4=1,2 I5=1,3 I6=2,3 I7=1,2,3 |
|
J1=1,2,3,5 J2=1,2,3,4,5 J3=2,3,4 J4=1,5 J5=2,3 J6=2,3,4 J7=Ø |
Se observa ca s-a obtinut o noua suma SKmin<aai sau abj, adica S4=34<40.
Se construieste o noua matrice (tabelul 45).
Tabelul 45
|
Bj AI |
B1 |
B2 |
B3 |
B4 |
B5 |
ai |
|
A1 | ||||||
|
A2 | ||||||
|
A3 | ||||||
|
bj |
Pentru solutia obtinuta se face o noua verificare:
S2=16+40=56
S3=14+10+12+10=46
S4=10+16+4+12+4=46
S5=10+14+10+12=46
S6=16+14+10+12+10=62
S7=40
|
I1=1 I2=2 I3=3 I4=1,2 I5=1,3 I6=2,3 I7=1,2,3 |
|
J1=1,2,3,5 J2=1,2,3,4,5 J3=2,3,4 J4=1,3,5 J5=2,3 J6=2,3,4 J7=0 |
|
S1=10+4+10+12+4=40 S2=16+40=56 S3=14+10+12+10=46 S4=10+16+4+12+4=46 S5=10+14+10+12=46 S6=16+14+10+12+10=62 S7=40 |
Deoarece este indeplinita conditia de incetare a aplicarii
metodei SKmin 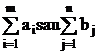 , inseamna ca solutia este optima si se efectueaza
repartitia in matricea din tabelul 45.
, inseamna ca solutia este optima si se efectueaza
repartitia in matricea din tabelul 45.
Se efectueaza
repartitia. Se pun necunoscutele ![]() in locurile
ocupate cu zero si zero in locurile unde
in locurile
ocupate cu zero si zero in locurile unde ![]() este
diferit de zero (tabelul 46).
este
diferit de zero (tabelul 46).
Tabelul 46
|
Bj Ai |
B1 |
B2 |
B3 |
B4 |
B5 |
ai |
|
A1 |
|
|
| |||
|
A2 |
|
| ||||
|
A3 |
|
|
| |||
|
bj |
Se repartizeaza
cantitatile din ultima coloana ![]() astfel incat sa
fie satisfacute necesitatile beneficiarilor
astfel incat sa
fie satisfacute necesitatile beneficiarilor ![]() , in modul urmator:
, in modul urmator:
- se completeaza
coloanele in care se afla o singura necunoscuta, repartizandu-se
cantitatea necesara indicata de ![]() ;
;
![]() ;
;
![]() ; rezulta
; rezulta ![]() ;
; ![]() ;
;
![]() ;
;
- se completeaza liniile in care exista o singura necunoscuta;
- se determina valorile celorlalte necunoscute, tinand seama de cele deja determinate.
Rezulta: ![]() ;
; ![]() ;
; ![]() .
.
Se trec valorile determinate
ale necunoscutelor ![]() in matricea cu datele
initiale (tabelul 47).
in matricea cu datele
initiale (tabelul 47).
Tabelul 47
|
Bj Ai |
B1 |
B2 |
B3 |
B4 |
B5 |
ai |
|
A1 | ||||||
|
A2 | ||||||
|
A3 | ||||||
|
bj |
Solutia finala si optima este cea data in matricea din tabelul 47 a carei functie scop are valoarea:
fmin=10 12=690 t.km.
Simularea consta in a crea variante care se apropie de ceea ce se intampla in realitate, ea fiind de fapt o metoda experimentala. De obicei SIAD reflecta realitatea complexa a fenomenelor si proceselor economice, si de aceea este greu de crezut ca un model matematic, cat ar fi el de bun, poate sa reflecte aceste procese. Simularea, prin diverse instrumente folosite imita ceea ce se intampla in realitate. Simularea inlocuieste in buna masura metodele de optimizare pentru rezolvarea problemelor complexe.
1.1. Definitii ale procesului simularii
Simularea este o forma de studiu a realitatii care foloseste ca forma de reprezentare modelul.
Definitia procesului simularii, in general, si a conceptului de simulare, in particular, este o problema dificila si controversata, deoarece la baza definirii stau cel putin trei aspecte complexe:
- natura problemei de rezolvat;
- obiectivul urmarit;
- stadiul dezvoltarii conceptului de simulare si cunostintele detinute.
Din punct de vedere etimologic, cuvantul provine din latinescul simulatio, care inseamna capacitatea de a reproduce, reprezenta sau imita ceva. Aceasta, cel putin tripla corespondenta, face dificila incercarea de a preciza o semnificatie general valabila a termenului de simulare pentru toate domeniile in care este intalnit.
Cert este insa faptul ca la baza procesului de simulare stau metodele de descriere, modelare si analiza o unor sisteme reale existente ori in curs de realizare (inclusiv in fazele de intuitie sau proiectare). Ca urmare, simularea ca element de studiu al realitatii foloseste ca baza tocmai modelele prin care aceasta este reprezentata. Cu alte cuvinte, simularea presupune intotdeauna utilizarea modelului si reprezinta, in esenta, o manipulare a acestuia.
Pentru prima data termenul de simulare a fost folosit de J. von Neumann si S. Ulam, in anii 1940-1944, cu privire la cercetarile de fizica nucleara efectuate in aceasta perioada in S.U.A. De atunci si pana acum au fost date numeroase definitii simularii, care, desi, pastreaza in esenta raportul de reprezentare prin modele si de manipulare a acestora, in sensul obtinerii unei corespondente intre dinamica realitatii si cea a manifestarii modelelor, se diferentiaza datorita greutatii pe care o confera, ca baza de studiu, unora din particularitatile de reprezentare sau interpretare.
De aceea, concomitent si fara a gresi, prin simulare se poate intelege (fig. 1.1):
o tehnica de construire a unei reprezentari a unui fenomen real, care trebuie studiat din punctul de vedere al comportamentului sau normal sau influentat de anumiti stimuli;
o analogie a unui fenomen real, bazata pe/sau reprezentata de o tehnica ce permite studiul unor fenomene complexe reproduse pe modele de laborator sau in teren;
o reprezentare dinamica a unei parti a lumii reale, realizata prin construirea unui model abstract ce poate fi miscat in timp sau direct influentat de acesta;
o metoda de cercetare bazata pe anticiparea rezultatelor unui ansamblu de ipoteze care au la baza elemente tehnice si relatiile dintre acestea;
o tehnica ce poate realiza o cale de testare, evaluare si manipulare a unui sistem fara a actiona direct asupra acestuia;
- o tehnica numerica pentru conducerea experimentelor pe un calculator, care implica anumite tipuri de modele matematice si logice care descriu comportarea viitoare a unui sistem;
- o tehnica de studiu a unor laturi ale comportamentului unui sistem, fara a actiona direct asupra lui, utilizand analogii fizice, chimice sau de calcul.
 |
Fig.1.1. Sinteza definitiilor simularii
O definitie formala a simularii o da Churchman, potrivit caruia:
Se spune ca sistemul X simuleaza sistemul Y daca si numai daca:
- X si Y sunt sisteme formale;
- Y este luat drept un sistem real;
- X este considerat o aproximare a sistemului real;- regulile de validitate din X sunt fara erori.
O definitie pragmatica, bazata pe posibilitatea utilizarii tehnicii de calcul in procesul simularii, o da Lucas (1976), potrivit caruia:
Simularea este o tehnica de realizare a experimentelor cu ajutorul calculatorului electronic, care implica utilizarea unor modele matematice sau logice ce descriu comportamentul sistemului real (sau a unor componente ale sale) pe durata unui interval de timp t, mic sau mare
In esenta, insa, simularea reprezinta o modalitate de a pune in corespondenta, pentru observare sau/si studiu, un fapt real cu un model pe care il manipuleaza in sensul obtinerii unei asemanarii de comportament. Ideala este similitudinea comportamentala care, conform definitiei lui Churchman, nu poate fi atinsa deoarece X, sistemul simulator al lui Y, este si ramane o aproximatie a acestuia.
1.2. Conceptele cu care opereaza simularea
Conceptele cu care opereaza simularea sunt concepte intalnite si la alte discipline, dar care, in contextul simularii, au fie semnificatie particulara, fie particularitati de interpretare.
Componenta - unitate identificabila, definibila, interconectabila cu una sau mai multe unitati ale sistemului. Se caracterizeaza prin stare iar evolutia comportamentului poate fi descrisa prin evolutia starilor.
Componenta cu initiativa - poate memora si clasifica informatii primite de la mediul inconjurator, luand decizii in conformitate cu anumite obiective.
Legatura - interactiune dintre doua componente sau dintre o componenta si mediul inconjurator (fig. 1.2):
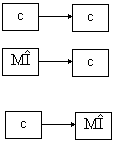 |
Fig.1.2 Legaturile componentelor
c c - evolutia unei componente (evenimentul) depinde de starile celeilalte;
c MI: legatura de intrare - intre mediul inconjurator si o componenta susceptibila de a genera un eveniment in sistem;
MI c: legatura de iesire - intre o componenta si mediul inconjurator afectat de schimbarea de stare a componentelor.
Sistem – multimea de componente integrate, in interactiune, cuprinzand operatori umani, echipamente tehnologice integrate functional in scopul realizarii unui obiectiv; are caracter mixt, adaptiv, perfectibil.
Entitate – element de abstractizare a realitatii.
Atribut – elementul sau elementele care descriu si caracterizeaza entitatea.
Subsistem – multime nevida de componente, interdependente printr-o multime de legaturi, astfel incat multimea acestor componente sa evolueze pentru realizarea unor obiective comune cu alte componente sau a unui subobiectiv al unui sistem.
Sistem (subsistem) echivalent (analog) (fig. 1.3) – se obtine prin eliminarea din sistemul de baza (original) a componentelor la care probabilitatea de aparitie a unui eveniment este redusa sau la care variatia starilor la aparitia evenimentelor este neglijabila, precum si prin eliminarea legaturilor cu probabilitatea de aparitie foarte redusa sau care genereaza evenimente cu probabilitate foarte redusa. Sistemul echivalent pastreaza din sistemul original numai laturile (functiile) esentiale, eliminand tot ce poate fi considerat nesemnificativ (elemente periferice, de design, redundante, cai duble). Sistemul echivalent poate fi realizat si din componente diferite fata de cele originale, pastrandu-se legaturile de baza, semnificative, in cadrul unor functionalitati similare.
Proiectarea sistemului – descrierea componentelor si a legaturilor in vederea reconstituirii si/sau modificarii (realizarii) unui sistem (nou), astfel ca acesta sa evolueze in vederea realizarii unor obiective date, respectand restrictiile impuse.
Stare – reuniunea tuturor atributelor asociate unei entitati (componente) care definesc starea acesteia. Starile entitatilor principale (sau dominante) descriu starea sistemului propriu-zis. In studiul unui proces ce are loc intr-un sistem, problema principala este intelegerea modului in care apar schimbarile de stare, posibilitatea de predictie a schimbarii starilor si controlul aparitiei lor. Combinatia acestor obiective se intalneste uneori sub denumirea de evaluare a variantelor (alternativelor).
Evaluarea variantelor – reprezinta studiul relatiilor existente intre sistem si mediul inconjurator, relatie ce genereaza schimbarile de stare ale sistemului.
Analiza modului in care sistemul afecteaza mediul extern este necesara masurarii schimbarilor de stare si a efectelor asupra evolutiei viitoare a sistemului.
Metode de evaluare a variantelor
- se determina legatura de intrare si reprezentarea sistemului dupa care se masoara legatura de iesire;
- se definesc legaturile de intrare si de iesire dupa care prin analiza si sinteza si structura sistemului care trebuie sa raspunda obiectivelor fixate;
- se considera sistemul cunoscut si se introduc intrarile care produc iesirile dorite (asteptate).
Marime – convertirea numerica a starilor si/sau a legaturilor si/sau a obiectivelor unui sistem.
Marime de intrare – marimea asociata unei legaturi de intrare, care poate fi modificata printr-o legatura de iesire si/sau prin rezultatul actiunii unui operator uman exterior sistemului. Este deci o marime care poate fi comandata.
Marime perturbatoare – marimea asociata unei legaturi de intrare ce nu poate fi comandata.
Marime de iesire – marimea asociata unei legaturi de iesire.
Eveniment – schimbarea de stare a unei entitati (componente).
Proces – o secventa de evenimente ordonate in timp.
Activitate – o reuniune de aplicatii ce transforma starea unei componente.
Performante – reprezinta o secventa de stari prin care sistemul trece intr-un interval de timp considerat, oferind informatii privind functionarea sa. Conceptul de performanta si modul de evoluare a acestora sunt dependente de natura sistemului considerat.
Obiectivul (ideal) al simularii este imbunatatirea performantelor sistemului simulat (existent sau in curs de proiectare, realizare). Operatia de imbunatatire implica, in general, investigarea si controlul unor aspecte ale sistemului, astfel ca in final sa se atinga performantele maxime posibile (de dorit cele optimale). Deoarece, in general, anumite aspecte depasesc posibilitatile de control ale analistului este necesara introducerea unor restrictii de diverse forme in functie de tipul sistemului.
Simulator – sistemul echivalent (analog) care genereaza o istorie (proces) asemanatoare cu istoria (procesul) sistemului studiat.
Model – descrierea abstracta a unui simulator. Modelul aproximeaza realitatea obiectiva, astfel ca oricat de laborios ar fi conceput, este totusi incomplet. Abaterile modelului fata de realitate depind de stadiul cunoasterii sistemului. Un model a carui evolutie corespunde destul de precis cu fenomenul real si care se obtine din acesta, prin neglijarea unor factori ce au influenta mica asupra evolutiei sistemului real, constituie un model idealizat al fenomenului real.
Modelare – tehnica de definire, cu ajutorul matematicii sau a altor metode, a sistemului sau a altor parti din sistem ori reprezentarea sistemului real printr-un sistem de alta natura mai usor de studiat.
Simulare – studiul unui sistem (subsistem) utilizand modele si/sau simulatoare. Simplificarile functionale se fac atat la nivelul intregului sistem, cat si la nivelul subsistemelor si al celorlalte componente.
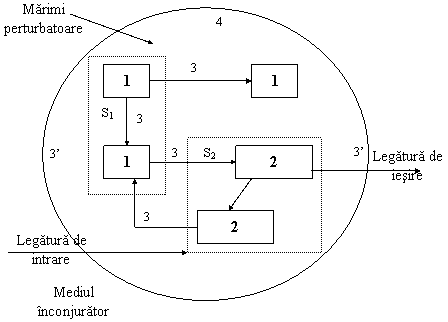 |
Fig.1.3 Structura unui sistem echivalent (analog)
– componenta
– componenta cu initiativa
– legatura c c si c subsistem
(3’) – legatura cu c-uri; de intrare si de iesire
- sistem cu doua subsisteme (S1) si (S2)
Sistem virtual - este alcatuit dintr-o reuniune de entitati, integrate descriptiv, fiecare fiind caracterizata prin atributele care o descriu si o definesc functional (comportamentul) in cadrul sistemului (fig.1.4).
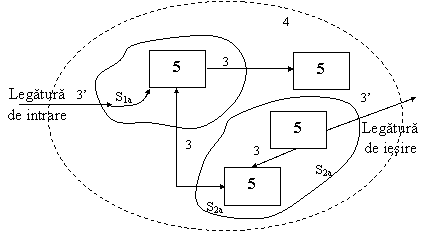 |
Fig. 1.4 Structura unui sistem virtual
|
In sistemele virtuale componentele se transforma in entitati si sunt definite prin atribute. Nu se schimba caracteristicile fundamentale ale legaturii cu mediu, obiectivul general si nici performantele (variabilele) definitorii.
1.3. Obiectivele simularii
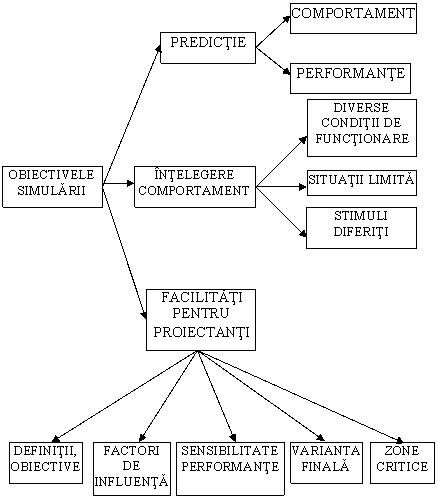
Se cunoaste faptul ca una din cele mai raspandite aplicatii o reprezinta proiectarea. Obiectivul proiectarii unui sistem sau proces este de a putea emite predictii asupra comportarii si performantelor sistemului respectiv, pe baza modelului (proiectului) si a unui set de informatii privind variabilele dominante ce determina evolutia sistemului (fig. 1.5).
Un alt obiectiv al simularii il constituie intelegerea comportarii sistemului real in diverse conditii de functionare, prin realizarea unei serii de simulari pentru diferite seturi de intrari. Acest lucru este posibil dupa ce modelul sistemului a fost construit si s-a stabilit cu o anumita certitudine ca respectivul model este o reprezentare valida a realitatii.
Un al treilea obiectiv al simularii il constituie studiul comportarii sistemului real in situatii limita sau sub influenta unor factori destabilizatori aleatorii (si care nu pot fi reprodusi), prin manipularea modelului in aceste limite si observarea performantelor si comportarii acestuia.
Al patrulea obiectiv al simularii il poate constitui studiul comportarii sistemelor fata de stimuli de mare intensitate, cu actiune de scurta durata, intr-o perioada mare de timp, in scopul determinarii caracteristicilor de siguranta in functionare a sistemelor reale.
De asemenea, simularea isi propune (un alt obiectiv) sa faciliteze proiectantilor:
- definirea problemei si a obiectivelor de studiu;
- evidentierea factorilor cu influenta asupra proiectarii;
- discernamantul relativ la sensibilitatea proiectului pentru un domeniu mare de parametri;
- selectarea formei finale a proiectului dintr-o multime de variante sau chiar si alternative;
- evidentierea deficientelor, corelatia dintre performante si specificatii, zonele sensibile si critice, comportamentul sistemului in timp real, indelungat, comprimat sau dilatat.
 |
1. Rezultatele simularii
Cea mai acceptata definitie considera simularea ca o tehnica de construire a unui model pentru un proces sau fenomen real, in vederea studierii comportamentului acestuia in conditii de experiment. Ca urmare, modelul folosit, numit model de simulare, are aici un sens mai larg deoarece el reprezinta atat realitatea (procesul, fenomenul), cat si modul de transformare a datelor de intrare in date explorabile, in vederea atingerii unui scop propus. Deci, prin simulare, in loc sa se obtina o varianta optimala ca in abordarile modelarii analitice (prin aplicarea unui algoritm), se obtin informatii descriptive privind fenomenul analizat prin experimente (fig.1.6). Cu alte cuvinte, rezultatele simularii se refera, de cele mai multe ori, la descriptorii care pot fi utilizati pentru prognoza comportamentului sau performantei sistemului in diverse conditii.
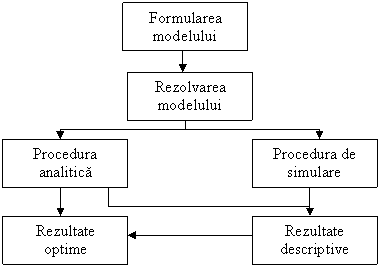 |
Fig.1.6 Schema simplificata a simularii
Desi rezultatele obtinute prin simulare au intotdeauna forma unor variante descriptive, exista uneori posibilitatea ca prin introducerea unei reguli sau a unui criteriu sa poata fi evaluate in asa fel incat sa se identifice cu o solutie optimala.
Simplificat, procesul de simulare mai poate fi prezentat intr-o structura liniara, in care modelul este o cutie neagra, iar controlul sau manipularea se face prin generarea unor marimi de intrare. Controlul manipularii se pune in evidenta prin performantele de la iesire (fig. 1.7).

Fig.1.7 Structura liniara a simularii
Procesul simularii impune, deci, generarea marimilor de intrare pentru a fi introduse in model, iar modelul le va prelucra in asa fel incat sa poata fi utilizate in masurarea sau evaluarea performantelor, variabilelor.
Pentru proiectarea unui model de simulare este necesar sa fie identificate cu atentie, in sistemul supus cercetarii, cele mai importante variabile ale sale si criteriile de performanta.
1.5. Caracteristicile simularii
Ca metoda de studiu a realitatii, simularea isi gaseste un loc bine conturat in procesul de selectare a metodelor de luare a deciziei, intre metodele intuitive si cele analitice, si poate fi utilizata separat (ca varianta independenta) sau in completare cu oricare din celelalte metode (fig. 1.8).
Simularea se diferentiaza de celelalte metode prin urmatoarele caracteristici:
- este o metoda formala ca si metodele bazate pe modele matematice, dar nu exclude, in timpul desfasurarii sale, elementele intuitive, euristice sau analitice;
- are caracter procedural, desfasurarea sa bazandu–se pe prelucrarea unor experimente create in cadrul modelului;
- permite o mai mare apropiere de realitate, datorita faptului ca in modelele de simulare se fac mai putine simplificari ale realitatii decat in celelalte metode;
- este adecvata pentru experimentele de conducere si decizie, realizand testarea valorilor specifice ale variabilelor decizionale din model si observarea impactului;
- este mai curand o descriere decat o unealta normativa; solutia optima nu este cautata automat;
- permite realizarea unui sir de experiente, obtinandu-se astfel o estimare a efectului total al unei actiuni;
- este adecvata studiului problemelor complexe (nu pot fi formulate matematic); nu se pot face ipoteze si implica o solutie practica sau economica.
    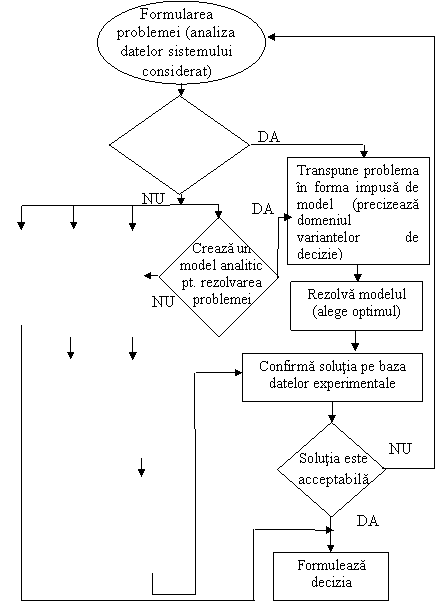 |
Fig.1.8 Relatia simulare cu alte metode de studiu
a realitatii
1.6. Avantajele si dezavantajele simularii
a) Avantajele simularii (fig. 1.9):
- permite studiul sistemelor reale, globale sau al situatiilor (starilor) fara a efectua modificari in evolutia lor reala;
- este folosita indeosebi in studiul si realizarea unor sisteme sau procese a caror desfasurare reala ar conduce la catastrofe (pierderi de vieti si valori materiale), oferind in final informatii asupra comportarii sistemelor reale date;
- ofera posibilitatea schimbarii conditiilor de intrare in sistem, la momentele de timp dorite, si a studierii efectelor acestor modificari la iesire, lucru imposibil in cadrul sistemelor reale ce sunt foarte complexe si cand parametrii lor nu pot fi controlati izolat;
- datorita temeiniciei analizei si a corelatiilor dintre variabile (marimi de intrare-parametri) poate dezvalui relatii ascunse sau viitoare imperfectiuni ale sistemului;
- desi modelul de simulare considera intreaga complexitate a sistemului, acesta poate fi construit interactiv, avand valente de integrare a mai multor modele simple; modelul de simulare poate fi deci construit pas cu pas;
- are un numar mare si divers de aplicatii, plecand de la probleme operationale si mergand pana la planificarea strategica;
- rezultatele descriptive oferite de simulare permit continuarea (adancirea) cercetarii pe calea analizelor senzitive (si daca?);
- permite o cunoastere “intima” a realitatii;
- asigura interferenta dintre experiment si sistemul real si permite, astfel, experimente pe diferite variabile pentru a le determina ponderea (importanta) in sistem si pe diferite politici sau variante pentru a le determina pe cele mai bune;
- nu necesita simplificari substantiale avand posibilitatea sa integreze in model complexitatea realitatii;
- poate realiza compresii sau dilatari de timp adecvate unor experimente si faciliteaza, astfel, o observatie normala a unor fenomene ce pot fi acoperite de curgerea nesesizabila a timpului;
- asigura o precizie corespunzatoare experimentelor si acuratete acceptabila.
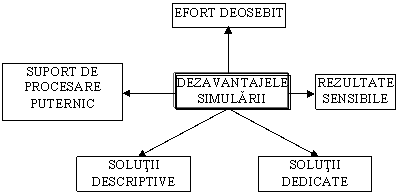
b) Dezavantajele simularii (fig. 1.10):
modelele de simulare necesita profesionalism si efort deosebit, o cunoastere si o interpretare justa a realitatii, date corecte si inter-relatii precise intre variabile, in special pentru problemele complexe;
- necesita un suport de procesare puternic sau mijloace dedicate procesului real;
- rezultatele simulari sunt foarte sensibile la consistenta modelului si la relatiile sale (de aproximare) cu realitatea;
- ofera doar solutii descriptive, de aceea, alegerea variantei optimale nu poate fi garantata; alegerea variantei optimale este, de fapt, un proces postsimulare;
- solutiile si concluziile pot fi transferate cu greu la alte probleme; simularea ramane dedicata unei anumite realitati.
 |
Fig. 1.9 Avantajele simularii
 |
Programul Access poate fi folosit ca instrument de lucru in realizarea sistemelor informatice pentru asistarea deciziei in cazul in care gradul de structurabilitate a deciziei depinde de experienta acumulata de decident si importanta
ei.
[i] Cap.4 / Modelarea sistemelor si proceselor, Gh. Ilie, I.Stoian, G. Alexandrescu, Editura Univesitatii Nationale de Aparare 'Carol I', Bucuresti, 2005
[ii] Cap.1 / Simularea sistemelor si proceselor, , G. Alexandrescu, I.Stoian, ,Gh. Ilie, Editura Univesitatii Nationale de Aparare 'Carol I', Bucuresti, 2005
|