Arborele binar de cautare reprezinta o solutie eficienta de implementare a structurii de date numite 'dictionar'. Vom considera o multime 'atomi'. Pentru fiecare element din aceasta multime avem: a I atomi, este definita o 838g67i functie numita cheie de cautare: key(a) I k cu proprietatea ca doi atomi distincti au chei diferite de cautare: a a T key(a key(a
Exemplu (abreviere, definitie) ('BST','Binary Search Tree')
('LIFO','Last In First Out') key(a) = a.abreviere
Un dictionar este o colectie S de atomi pentru care se definesc operatiile:
insert(S,a) insereaza atomul a in S daca nu exista deja;
delete(S,k) sterge atomul cu cheia k din S daca exista;
search(S,k) cauta atomul cu cheia k in S si-l returneaza sau determina daca nu este.
O solutie imediata ar fi retinerea elementelor din S intr-o lista inlantuita, iar operatiile vor avea complexitatea O(n).
Acestea sunt o alta solutie
pentru a retine elementele din
cel mai defavorabil: O(n);
mediu: O(log n).
Un arbore binar de cautare este un arbore T ale carui noduri sunt etichetate cu atomii continuti la un moment dat in dictionar.
T = (V, E │V│ = n. (n atomi in dictionar)
Considerand r I V (radacina arborelui), Ts subarborele stang al radacinii si Td subarborele drept al radacinii, atunci structura acestui arbore este definita de urmatoarele proprietati:
un nod x I Ts atunci key(data(x)) < key(data(r));
x I Td atunci key(data(x)) > key(data(r));
Ts si Td sunt BST.
Observatii:
Consideram ca pe multimea k este definita o relatie de ordine (de exemplu lexico-grafica);
Pentru oricare nod din BST toate nodurile din subarborele stang sunt mai mici decat radacina si toate nodurile din subarborele drept sunt mai mari decat radacina.
Exemple: 15 15
/ /
7 25 10 25
/ / / /
40 2 1 7 13
/ /
9
este BST nu este BST.
3) Inordine: viziteaza nodurile in ordine crescatoare a cheilor: 2 7 9 13 15 17 25 27 40 99
Search:
search(rad,k) // rad pointer la radacina arborelui
Insert:
Se va crea un nod in arbore care va fi plasat la un nou nod terminal. Pozitia in care trebuie plasat acesta este unic determinata in functie de valoarea cheii de cautare.
Exemplu: vom insera 19 in arborele nostru:
15
/
7 25
/ /
17 40
9 19
insert(rad,a) // rad referinta la pointerul la radacina // arborelui
Functia make_nod creaza un nou nod:
make_nod(a)
Observatie:
La inserarea unui atom deja existent in arbore, functia insert nu modifica structura arborelui. Exista probleme in care este utila contorizarea numarului de inserari a unui atom in arbore.
Functia insert poate returna pointer la radacina facand apeluri de forma p= insert(p,a).
Delete:
delete(rad,k) // rad referinta la pointer la radacina
Stergerea radacinii unui BST.:
rad T arbore vid
a) rad sau b) rad T a) SAS sau b) SAD
/
SAS SAD
delete_root(rad) // rad referinta la pointer la radacina
15
/
7 25
/ /
2 13 17 40
/ /
9 27
/
Detasarea din structura arborelui BST a celui mai mare nod (remove_greatest):
Pentru a gasi cel mai mare nod dintr-un arbore binar de cautare, se inainteaza in adancime pe ramura dreapta pana se gaseste primul nod care nu are descendent dreapta. Acesta va fi cel mai mare.
Vom trata aceasta procedura recursiv:
Caz1: rad T se returneaza pointer la radacina si arborele rezultat va fi vid.
Caz2: rad T se returneaza pointer la radacina si arborele rezultat va fi format doar din SAS subarborele stang (SAS).
Caz3 rad T functia returneaza pointer la cel mai mare nod din SAD, iar rezultatul va fi SAS arborele care este fomat din radacina,SAS si SAD cel mai mare nod.
remove_greatest(rad) //rad -referinta la pointer la //radacina: un pointer la radacina de poate
//fi modificat de catre functie
Observatie:
Functia remove_greatest modifica arborele indicat de parametru, in sensul eliminarii nodului cel mai mare, si intoarce pointer la nodul eliminat.
Demonstratia eficientei (complexitate)
Complexitatea tuturor functiilor scrise depinde de adancimea arborelui. In cazul cel mai defavorabil, fiecare functie parcurge lantul cel mai lung din arbore. Functia de cautare are, in acest caz, complexitatea O(n).
Structura arborelui BST este determinata de ordinea inserarii.
De exemplu, ordinea 15 13 12 11 este alta decat 15 12 11 13 .
Studiem un caz de complexitate medie:
Crearea unui BST pornind de la secventa de atomi (a a an
gen_BST (va fi in programul principal)
| rad= 0
| for i= 1 to n
| insert (rad, ai)
Calculam complexitatea medie a generarii BST:
Complexitatea in cazul cel
mai defavorabil este: ![]()
Notam cu T(k) numarul de comparatii mediu pentru crearea unui BST pornind de la o secventa de k elemente la intrare. Ordinea celor k elemente se considera aleatoare.
Pentru problema T(n) avem de creat secventa (a a an cu observatia ca a este radacina arborelui. Ca rezultat, in urma primei operatii de inserare pe care o facem, rezulta:
a1
/
a1 ai
(ai<a1) (ai>a1)
Nu vom considera numararea operatiilor in ordinea in care apar ele, ci consideram numarul de operatii globale. Dupa ce am inserat a , pentru inserarea fiecarui element in SAS sau SAD a lui a , se face o comparatie cu a . Deci:
T(n)= (n - 1) + val.med.SAS + val.med.SAD
val.med.SAS = valoarea medie a numarului de comparatii necesar pentru a construi subarborele stang SAS
val.med.SAD = valoarea medie a numarului de comparatii necesar pentru a construi subarborele drept SAD
![]()
Notam:
Ti(n) = numarul mediu de comparatii necesar pentru construirea unui BST cu n noduri atunci cand prima valoare inserata (a ) este mai mare decat i-1 dintre cele n valori de inserat. Putem scrie:
![]()
![]()
Deci:
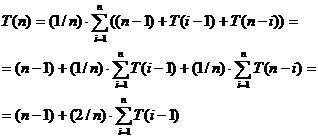
Deci:
![]()
Complexitatea acestei functii este: O(n ln n) (vezi curs 5 complexitatea medie a algoritmului Quick-Sort)
Definitie
Un arbore binar este echilibrat daca si numai daca, pentru fiecare nod din arbore, diferenta dintre adancimile SAS si SAD in modul este
Exemple:
a a
/ /
b c b c
/ / /
d e f g d e f
/
g h
arbore binar arbore binar
complet echilibrat echilibrat
Adancimea unui arbore echilibrat cu n noduri este O(ln n).
Se completeaza operatiile insert si delete cu niste prelucrari care sa pastreze proprietatile de arbore binar echilibrat pentru arborele binar de cautare. Arborele binar echilibrat este un BST echilibrat, proprietatea de echilibrare fiind conservata de insert si delete. Efortul, in plus, pentru completarea operatiilor insert si delete nu schimba complexitatea arborelui binar echilibrat.
Modificarile care se vor face se vor numi rotatii.
Caz 1: Fie arborele echilibrat
A
/
B T3 h = depth(T ) = depth(T ) = depth(T
/
T T
Consideram arborii T1, T , T echilibrati. Inserand un nod prin rotatie simpla, rezulta structurile rotit simplu la dreapta si rotit simplu la stanga imaginea oglinda a rotatiei dreapta:
A A
/ /
B T T B
/ /
T T T T
Caz 2: Inserarea se face prin rotatii duble:
A A
/ /
B T T B
/ /
T T T T
rotatie dubla rotatie dubla
la dreapta la stanga
Fie primul caz:
A
/
B T
/
T T este BST: T < B < T < A < T
Toti arborii care respecta in continuare aceasta conditie vor fi BST.
Ridicand pe B in sus, si notand cu // legaturile neschimbate, rezulta:
B
//
// A
T
___________ _T _T pe aceeasi
linie
care este un BST , deci este arbore echilibrat, si are aceeasi adancime (!!!) cu arborele initial (de dinainte de inserare). Nodurile superioare nu sunt afectate. Rationament analog pentru imaginea oglinda.
Fie cazul 2: Pentru rotatia dubla se detaliaza structura arborelui T . Nu se poate sparge arborele initial ca in cazul 1.
A
/
B
// T
// C
T T2S T2D
depth(T ) = depth(T ) = h
depth(T2S) = depth(T2D) = h - 1
In urma inserarii, unul dintre arborii T2S si T2D isi
mareste adancimea. Aplicam aceiasi tehnica:
T <
B < T2S < C < T2D < A < T
Incepem cu C:
C
/
B A
// /
// T2S T2D
____T T
la acelasi nivel
Rezulta un BST echilibrat, de
aceeaai adancime cu arborele initial. Rotatiile sunt duble,
in sensul ca
s-a facut o rotatie simpla B la stanga cu o rotatie simpla A la dreapta.
r pointer la nodul radacina (A)
a pointer la radacina
p = lchild(r) b = lchild(a)
lchild(r) = rchild(p) lchild(a) = rchild(b)
rchild(p) = r rchild(b) = a
r = p a = b
b = lchild(a)
c = rchild(b)
lchild(a) = rchild(c)
rchild(b) = lchild(c)
rchild(c) = a
lchild(c) = b
a = c // se schimba radacina arborelui.
Asadar, in inserarea prin rotatie se obtine un arbore echilibrat cu adancimea egala cu adancimea arborelui de dinainte de inserare. La inserarea unui nod terminal intr-un arbore AVL este necesara aplicarea a cel mult o rotatie asupra unui nod. Trebuie, deci sa gasim nodul asupra caruia trebuie aplicata rotatia. Reprezentam ramura parcursa de la radacina la nodul inserat:
x T bf = 1
y T bf = 0
z T bf = - 1 (bf = -2 dupa inserare)
w T bf = 0 (bf = 1 dupa inserare)
v T bf = 0 (bf = -1 dupa inserare)
nodul
inserat
S-a notat pentru fiecare nod bf balance factor (factor de dezechilibrare):
bf(nod) = depth (lchild (nod)) depth (rchild (nod))
adica este diferenta dintre adancimea subarborelui stang si adancimea subarborelui drept.
Calculam factorii de balansare dupa inserare.
Observatie: Pentru nodul terminal s-a schimbat adancimea si factorul de balansare; bf = -2 dupa inserare devine nod dezechilibrat. Trebuie aplicata, deci, echilibrarea.
Definitie:
Se numeste nod critic primul nod cu bf 0 intalnit la o parcurgere de jos in sus a ramurii care leaga nodul inserat de radacina.
Observatie: Toate nodurile din ramura
care sunt pe nivele inferioare nodului critic vor capata bf = 1 sau
bf = -1.
La nodul critic exista doua situatii:
Nodul critic va fi perfect balansat (bf = 0), daca dezechilibrul creat de nodul inserat anuleaza dezechilibrul initial al nodului. In acest caz nu este nevoie de rotatie (el completeaza un gol in arbore).
Factorul de balansare devine bf = 2 sau bf = -2 atunci cand nodul inserat mareste dezechilibrul arborelui (s-a inserat nodul in subarborele cel mai mare). In acest caz, se aplica o rotatie in urma careia se schimba strucutra subarborelui, astfel incat noua radacina capata bf = 0, conservandu-se adancimea.
Concluzie: Problema conservarii proprietatii de echilibrare a arborelui se rezolva aplicand o rotatie asupra nodului critic numai atunci cand inserarea dezechilibreaza acest nod.
Costul suplimentar care trebuie suportat se materializeaza prin necesitatea ca in fiecare nod sa se memoreze factorul de dezechilibrare bf. Acesti factori de dezechilibrare vor fi actualizati in urma operatiilor de rotatie si inserare. Operatia de stergere intr-un AVL implica mai multe rotatii, ea nu se studiaza in acest curs.
Exemplu: Se da arborele cu urmatoarea structura:
55
20 80
/
10 35 90
/ /
5 30
Sa se insereze nodurile 15, apoi 7 si sa se echilibreze arborele
Inseram prima valoare 15. Comparam mai intai cu e in stanga lui, s.a.m.d. pana cand gasim locul ei in pozitia de mai jos. Pentru a doua valoare de inserat, 7, nodul critic este 55. El este dezechilibrat stanga. Deci, va fi echilibrat la valoarea 2. Este necesara aplicarea unei rotatii asupra radacinii.
55
/
20 80
/
10 35 90
5
7
Facem o identificare cu unul din desenele de echilibrare prezentate in cursul anterior. Se asociaza nodurile: 55 A
20 B etc.
T
20 ----------> noduri implicate
in
10 > rotatie
/ /
5 80
/
7 30 90
In urma unei rotatii simple, factorii de dezechilibru implicati in rotatie devin zero.
Fie o a treia valoare de inserat 3, apoi a patra 9:
Nodul critic pentru 3 este 5, iar pentru 9 este este 10. Dupa rotatia aplicata (T2D, T2S vizi), rezulta arborele:
20
/
7 55
/ /
5 10 35 80
/ / /
3 30 90
La rotatia dubla, daca nodul
B are bf = 0 |
A are bf = -1 | exceptie facand nodul C nodul de inserat
La rotatia dubla, daca nodul
B are bf = 1 |
A are bf = 0 | exceptie facand nodul C nodul de inserat
In acest mod de reprezentare se reprezinta arborele printr-un tablou. Fie un arbore binar complet:
a
/
b c
/ /
d e f g
h i j k l m n o
care are 4 nivele, deci 24 - 1 = 15 noduri.
Asociem acestui arbore un vector V:
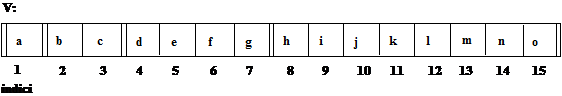
structurat astfel: radacina, nivelul 1 de la stanga la dreapta, nodurile nivelului 2 de la stanga la dreapta, etc, despartite de linii duble.
Lema
Daca in vectorul V un nod x este reprezentat prin elementul de vector V(i), atunci:
left_child(x) este reprezentat in elementul de vector V [2·i];
right_child(x) este reprezentat in elementul de vector V [2·i + 1];
parent(x) este reprezentat in elementul de vector V [[i/2]]
cu observatia ca paranteza patrata interioara este partea intrega.
Demonstratie:
Se face inductie dupa i:
Pentru i = 1 T V[1] radacina
T V[2] left_child(rad)
T V[3] right_child(rad)
Presupunem adevarata lema pentru elementul V[i] T V[2i] left_child
V[2i + 1] right_child
Elementul V[i + 1] este nodul urmator (de pe acelsi nivel sau de pe nivelul urmator) intr-o parcurgere binara.
V[i + 1] T left_child in V[2i + 2] = V[2(i + 1)]
right_child in V[2i + 3] = V[2(i + 1) + 1]
Daca avem un arbore binar care nu este complet, reprezentarea lui implicita se obtine completandu-se structura arborelui cu noduri fictive pana la obtinerea unui arbore binar complet.
Definitie:
Se numeste arbore heap un arbore binar T = (V, E) cu urmatoarele proprietati:
functia key : V R care asociaza fiecarui nod o cheie.
un nod v I V cu degree(v) > 0 (nu este nod terminal), atunci:
key(v) > key(left_child(v)), daca left_child(v)
key(v) > key(right_child(v)), daca right_child(v)
(Pentru fiecare nod din arbore, cheia nodului este mai mare decat cheile descendentilor).
Exemplu: 99
/
50 30
/ /
45 20 25 23
Observatie: De obicei functia cheie reprezinta selectia unui subcamp din campul de date memorate in nod.
Coada cu prioritate;
Algoritmul Heap_Sort
Arborii heap nu se studiaza complet in acest curs.
Este o structura de date pentru care sunt definite urmatoarele operatii:
insert (S,a) - insereaza un atom in structura,
remove (S) - extrage din structura atomul cu cheia cea mai mare.
O coada cu prioritati poate fi implementata printr-o lista. Implementarea cozii cu prioritati prin lista permite definirea operatiilor insert si remove, in cazul cel mai bun, una este de complexitate O(1) si cealalta este de complexitate O(n).
Implementarea cozii cu prioritati prin heap face o echilibrare cu complexitatea urmatoare: una este de complexitate 0(log n) si cealalta de complexitate 0(log n).
/
heap /
/ 50
/ /
30
/ / /
37 12 2
/ / / _________
15 7 | 42
----- ----- -------|
Acelasi arbore in reprezentare implicita:

Operatiile insert si remove pentru arbori heap au o forma foarte simpla cand utilizeaza reprezentarea implicita. Consideram, in continuare, arbori heap in reprezentare implicita.
Exemplu: un arbore cu ultimul nivel avand toate nodurile aliniate la stanga:
Inseram valoarea 42 T se adauga nodul la un nivel incomplet;
In reprezentarea implicita se adauga nodul la sfarsit.
insert
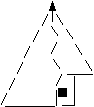
1) In reprezentarea implicita: V [N + 1] = a
N = N + 1
In continuare reorganizam structura arborelui astfel incat sa-si pastreze structura de heap.
2) Se utilizeaza interschimbarile. Comparatii:
Iau 2 indici: child = N si
parent = [N/2]
(in cazul nostru N = 11 si [N/2] = 5)
Comparam V[child] cu V[parent]
Interschimbare daca V[child] nu este mai mic decat V[parent] (se schimba 42 cu 37)
3) Inaintare in sus: child = parent
parent = [child/2]
4) Se reia pasul 2) pana cand nu se mai face interschimbarea.
Structura S este un arbore heap. El se afla in reprezentare implicita in 2 informatii:
V vector
N dimensiune
insert(V, N, a) // V vectorul ce contine reprezentarea
// implicita a heapu-lui;
// N numarul de noduri din heap,
// ambele sunt plasate
// prin referinta (functia insert
// le poate modifica);
// a atomul de inserat;
50
/
/ /
33 40 40 20
/ /
10 15 7 37 39
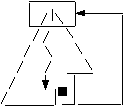
se scoate elementul cel mai mare care este radacina heap-ului; se initializeaza cei 2 indici;
se reorganizeaza structura arborilor: se ia ultimul nod de pe nivelul incomplet si-l aduc in nodul-radacina, si aceasta valoare va fi retrogradata pina cand structura heap-ului este realizata.
parent
conditia de heap /
lchild rchild
parent = max(parent, lchild, rchild).
Exista trei cazuri:
conditia este indeplinita deodata;
max este in stanga T retrogradarea se face in stanga;
max este in dreapta T retrogradarea se face in dreapta.
remove(V, N)
In cazul cel mai defavorabil se parcurge o ramura care leaga radacina de un nod terminal. La insert avem o comparatie, iar la remove avem doua comparatii. Rezulta, complexitatea este data de adancimea arborelui. Daca N este numarul de noduri din arbore, 2k N k+1 , si adancimea arborelui este k+1.
2k - 1 < N k+1 T k = [log N]
| |
nr. de noduri nr. de noduri
ale arborelui ale arborelui
complet de complet de
adancime k adancime k+1
k log N < k + 1 T adancimea arborelui este k = [log N]
Deci complexitatea este O(log N).
A doua aplicatie a heap-urilor este algoritmul Heap_Sort.
Heap_Sort(V, n)
Aceasta procedura sorteaza un vector V cu N elemente: transforma vectorul V intr-un heap si sorteaza prin extrageri succesive din acel heap.
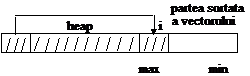
heap_sort
Observatii:
Se fac mai multe operatii insert
in heap-uri a
caror dimensiune creste de la 1
Se fac n-1 opera_ii insert in heap-uri cu dimensiunea N n
Rezulta complexitatea acestor operatii nu depaseste O(n log n). Facem un studiu pentru a vedea daca nu cumva ea este mai mica decat O(n log n)
Cazul cel mai defavorabil este situatia in care la fiecare inserare se parcurge o ramura completa. De fiecare data inserarea unui element se face adaugand un nod la ultimul nivel. Pentru nivelul 2 sunt doua noduri. La inserarea lor se va face cel mult o retrogradare (comparatie).
Pe ultimul exemplu de arbore, avem:
nivelul : 2 noduri 1 comparatie
nivelul : 4 noduri 2 comparatii
nivelul : 8 noduri 3 comparatii
nivelul i : 2i-1 noduri i-1 comparatii
Considerand un arbore complet (nivel complet) T N = 2k - 1 T numarul total de comparatii pentru toate nodurile este T(n) de la nivelul 2 la nivelul k. Vom calcula:
![]()
Sa aratam: ![]()
cu tehnica ![]() . Asadar:
. Asadar:
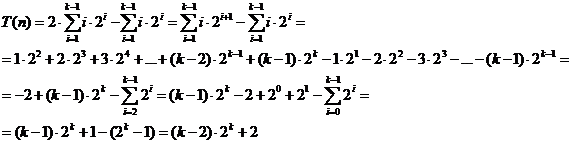
Rezulta: ![]()
iar ![]() ,
,
din ![]()
Rezulta: ![]()
----- ----- ----- ----- ----
termen dominant
Facandu-se majorari, rezulta complexitatea O(n log n).
Prezentam acum alta strategie de obtinere a heap_gen cu o complexitate mai buna:
Construim heap-ul de jos in sus (de la dreapta spre stanga). Cele mai multe noduri sunt la baza, doar nodurile din varf parcurg drumul cel mai lung.
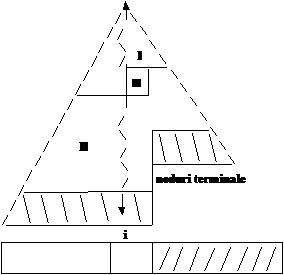
Elementele V[i+1,N] indeplinesc conditia de structura a heap-ului:
j >i avem: V[j] > V[2*j] , daca 2*j N
V[j] > V[2*j +1] , daca 2*j + 1 N
Algoritmul consta in adaugarea elementului V[i] la structura heap-ului. El va fi retrogradat la baza heap-ului (prelucrare prin retrogradare):
retrogradare(V, N, i)
In aceasta situatie, vom avea:
heap_gen
Fie un arbore complet cu n = 2k Cazul cel mai defavorabil este situatia in care la fiecare retrogradare se parcurg toate nivelele:
nivel k : nu se fac operatii
nivel k-1 : 2k-2 noduri o operatie de comparatie
nivel k-2 : 2k-3 noduri 2 operatii
nivel i : 2i-1 noduri k-i operatii
nivel : 2 noduri k-2 operatii
nivel : 2 noduri k-1 operatii
Se aduna, si rezulta: ![]()
Tehnica de calcul este aceeasi: ![]()
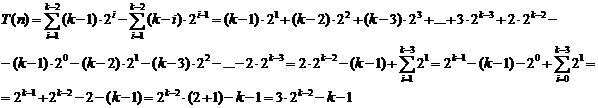
Rezulta: ![]()
![]()
termen dominant
Rezulta complexitatea este O(n). Comparand cu varianta anterioara, in aceasta varianta (cu heap-ul la baza) am castigat un ordin de complexitate. Rezulta, complexitatea algoritmului Heap_Sort este determinata de functiile remove ce nu pot fi aduse la mai putin de complexitate O(log n). Rezulta:
Heap_Sort = O(n) + O(n·log n)
----- ----- -----
termen ce determina complexitatea
Rezulta complexitatea alg. Heap_Sort = O(n·log n)
|