Presupune adaugarea unui element intr-o pozitie specificata in lista. Exista posibilitati diferite de a specifica pozitia in care vrem sa inseram elementul:
Situatia in care pozitia de inserat este data printr-un numar care sa indice al catelea element trebuie sa fie in lista elementul inserat;
Situatia in care pozitia de inserat este data prin valoarea atomului dupa care sau inainte de care se face inserarea;
Situatia in care pozitia de inserat poate fi data implicit prin valoarea atomului de inserat.
Inserarea in fata unui element specificat
Functia inscrie un element in fata altui element dintr-o lista:
insert (l, a, b)
// l lista (pointer la primul element)
// a valoarea atomului de inserat
// b valoarea atomului in fata caruia se insereaza
else
Operatia delete sterge un atom dintr-o lista. Deci vom avea in pseudocod, o functie de forma:
delete(l, a)
// l lista
// a valoarea atomului care trebuie sters
Operatia de parcurgere a listei inlantuite consta dintr-o secventa de instructiuni care se foloseste de fiecare data cand dorim sa prelucram elementele listei intr-un anumit scop.
O parcurgere a listei presupune o prelucrare efectuata asupra fiecarui element din lista (asadar nu o functie, ci o secventa de instructiuni):
Fie p pointer-ul care indica pe rand fiecare element al listei, si consideram ca p incepe cu l:
while (p!=0) do |¯ prelucrare (data(p)) // ex:afisarea //atomului
|_ p=link(p) // trece la urmatorul
O stiva este o structura de date de tip 'container' (depoziteaza obiecte de un anumit tip) organizata dupa principiul LIFO (Last In First Out).
Operatiile de acces la stiva (push ‑ adauga un element in stiva si pop ‑ scoate un element din stiva) sunt create astfel incat pop scoate din stiva elementul introdus cel mai recent.
O stiva este un caz particular de lista, si anume este o lista pentru care operatiile de acces (inserare, stergere, accesare element) se efectueaza la un singur capat al listei.
Daca STACK este de tip stiva si ATOM tipul obiectelor continute in stiva atunci operatiile care definesc tipul structura de stiva pentru tipul STACK sunt:
CREATE() STACK
Operatia CREATE nu primeste parametri, creeaza o stiva care pentru inceput este vida (nu contine nici un obiect).
PUSH(STACK, ATOM) STACK
Operatia PUSH primeste ca parametri o stiva si un obiect si produce stiva modificata prin adaugarea obiectului in stiva.
POP(STACK) STACK, ATOM
Operatia POP primeste ca parametri o stiva pe care o modifica scotand un obiect. De asemenea produce ca rezultat obiectul scos din stiva.
TOP(STACK) ATOM
Operatia TOP intoarce ca rezultat obiectul din varful stivei pe care o primeste ca parametru.
ISEMPTY(STACK) boolean
Operatia ISEMPTY este folosita pentru a testa daca stiva este vida.
Facem notatiile:
S stiva
S.vect vectorul in care se reprezinta elementele stivei S
S.sp indicele varfului stivei
Elementele sunt memorate asadar unul dupa altul in vectori, nefiind neaparat in ordine crescatoare. Zona de memorat trebuie sa contina aceste doua informatii: S.vect si S.sp grupate intr-o structura:
struct Stack ;
Conditia de stiva vida este: S.sp=0
Se scrie:
push(S,a)
Functia pop scoate un element din stiva:
pop(S)
Observatie: Se obisnuieste ca pe langa stergerea elementului, functia pop sa returneze elementul scos din lista.
top(S)
Functia isEmpty(S) testeaza conditia stiva vida:
isEmpty(S)
O stiva poate fi implementata ca o lista inlantuita pentru care operatiile de acces se fac numai asupra primului element din lista. Deci, operatia PUSH va insemna inserare in prima pozitie din lista (in fata) iar POP va insemna stergerea primului element din lista. Pentru a manevra o stiva vom avea nevoie de un pointer la primul element din inlantuire, deci, vom echivala tipul Stack cu tipul 'pointer la element de lista', iar functiile care implementeaza operatiile de acces vor avea aceleasi prototipuri cu cele date mai sus.
struct Element ;
typedef Element* Stack;
Fie S pointer-ul la primul element din inlantuire, se echivaleaza tipul Stack cu typedef Element* Stack, iar conditia de stiva vida este S=0 :
push(S,a)
pop(S)
top(S)
isEmpty(S)
Stivele sunt cele mai simple structuri de date, ele avand si operatiile imediate.
O coada este o lista in care operatiile de acces sunt restrictionate la inserarea la un capat si stergerea de la celalat capat.

Pricipalele operatii de acces sunt:
PUT(Coada, Atom) Coada
Adauga un element la coada.
GET(Coada) Coada, Atom
Scoate un Atom din coada.
Returneaza atomul scos.

O coada poate fi organizata pe un spatiu de memorare de tip tablou (vector).
Sunt necesari doi indicatori:
head indica: primul element care urmeaza sa fie scos.
tail indica: locul unde va fi pus urmatorul element adaugat la coada.
Conditia 'coada vida' este echivalenta cu: head = tail. Initial indicatorii vor fi initializati astfel incat sa indice ambii primul element din vector.
Operatia PUT inseamna:
‑ V[tail] primeste Atomul adaugat;
‑ incrementeaza tail.
Operatia GET inseamna:
‑ intoarce V[head];
‑ incrementeaza head
Se observa ca adaugari si stergeri repetate in coada deplaseaza continutul cozii la dreapta, fata de inceputul vectorului. Pentru a evita acest lucru ar trebui ca operatia GET sa deplaseze la stanga continutul cozii cu o pozitie. Primul element care urmeaza sa fie scos va fi intotdeauna in prima pozitie, indicatorul head pierzandu‑si utilitatea. Dezavantajul acestei solutii consta in faptul ca operatia GET necesita o parcurgere a continutului cozii.
Facem notatiile:
C coada
C.vect vectorul in care sunt memorate elementele cozii
C.head indicele elementului ce va fi scos din coada la urmatoarea operatie get
C.tail indicele (pozitia) in care va fi memorat urmatorul element adaugat la coada.
Conditia coada vida este C.head=C.tail.
Functia put pune in coada C un atom a:
put(C,a)
Functia get scoate un element din coada si-l returneaza:
get(C)
isEmpty(C)
Pentru a obtine o coada circulara vom porni de la o coada liniara simpla (cu doi indicatori) si vom face in asa fel incat la incrementarea indicatorilor head si tail, cand acestia ating ultima pozitie din vector sa se continue cu prima pozitie din vector.
Functia urmatoare poate realiza aceasta cerinta:
int nextPoz(int index)
unde DIMVECTOR este dimensiunea vectorului in care se memoreaza elementele cozii.
Continutul cozii va arata asa:
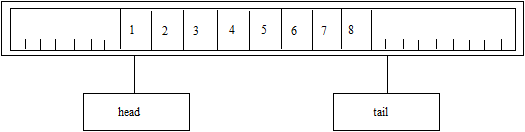
sau asa:
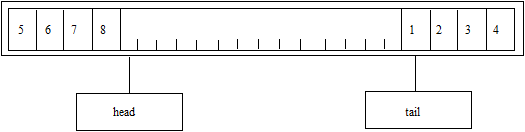
Conditia 'coada vida' ramane echivalenta cu: head = tail
Coada va fi plina daca: head=1 si tail=DIMVECTOR
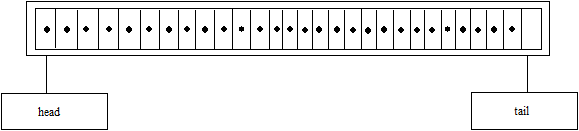
sau daca: tail+1 = head
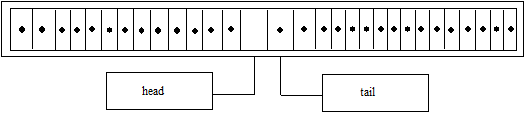
Ambele situatii sunt continute in conditia:
nextPoz(tail) = head // conditia 'coada plina'
Coada circulara ordonata asigura reutilizarea spatiului eliberat de get la urmatoarele inserari in coada.
Observatie:
In coada circulara de dimensiune DIMMAX pot fi memorate DIMMAX elemente.
'Coada plina' se realizeaza in 2 situatii:
a) C.head=1 si C.tail=DIMMAX
b) C.tail+1=C.head
Iar, conditia C.head=inc(C.tail) le contine pe amandoua.
In cazul cozilor circulare se modifica doar operatiile put si get:
put(C,a)
get(C)
|