REPREZENTAREA sI TRAVERSAREA GRAFURILOR
Continutul lucrarii
În lucrare sunt prezentate câteva notiuni legate de grafuri, modurile de reprezentare si traversare a lor.
Consideratii teoretice 525e42f
Notiuni de baza
Graful orientat sau digraful G =(V, E) este perechea formata din multimea V de vârfuri si multimea E V rV de arce. Un arc este o pereche ordonata de vârfuri (v, w), unde v este baza arcului, iar w este vârful arcului. In alti termeni se spune ca w este adiacent lui v.
O cale este o succesiune de vârfuri v[1],v[2],.,v[k], astfel ca exista arcele (v[1],v[2]), (v[2],v[3]),.,(v[k-1],v[k]) în multimea arcelor E. Lungimea caii este numarul de arce din cale. Prin conventie, calea de la un nod la el însusi are lungimea 0.
O cale este simpla, daca toate vârfurile, cu exceptia primului si ultimului sunt distincte între ele.
Un ciclu este o cale de la un vârf la el însusi.
Un graf orientat etichetat este un graf orientat în care fiecare arc si /sau vârf are o eticheta asociata, care poate fi un nume, un cost sau o valoare de un tip oarecare.
Un graf orientat este tare conex, daca oricare ar fi vârfurile v si w exista o cale de la v la w si una de la w la v.
Un graf G' =(V', E') este subgraf al lui G daca V' V si E' E. Se spune ca subgraful indus de V' V este G' =(V', E (V'rV')).
Un graf neorientat sau prescurtat graf G =(N, R) este perechea formata din multimea N de noduri si multimea R de muchii. O muchie este o pereche neordonata (v, w)=(w, v) de noduri.
Definitiile prezentate anterior ramân valabile si în cazul grafurilor neorientate.
Moduri de reprezentare
Atât grafurile orientate, cât si cele neorientate se reprezinta frecvent sub doua forme: matricea de adiacente si listele de adiacente.
Astfel, pentru graful orientat G =(V, E), unde V este multimea vârfurilor V =,matricea de adiacente A va fi definita astfel :

Matricea de adiacente
etichetata A (sau matricea costurilor) va fi definita astfel :
Matricea de adiacente este simetrica pentru grafuri neorientate si nesimetrica pentru cele orientate.
![]()
Matricea de adiacente este
utila când se testeaza frecvent prezenta sau absenta unui
arc si este dezavantajoasa când numarul de arce este mult mai
mic decât n x n.
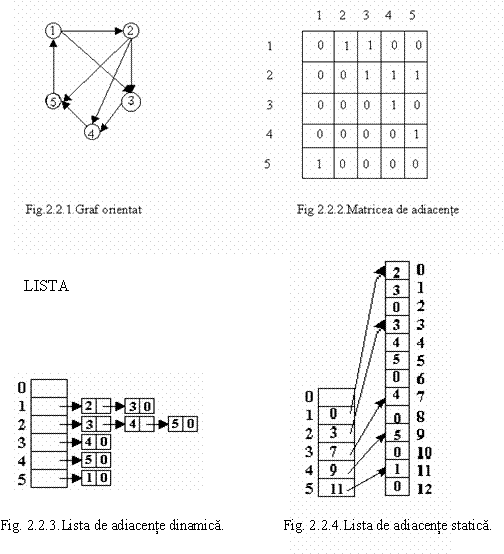
Reprezentarea prin liste de adicente foloseste mai bine memoria, dar cautarea arcelor este mai greoaie. În aceasta reprezentare, pentru fiecare nod se pastreaza lista arcelor catre nodurile adiacente. Întregul graf poate fi reprezentat printr-un tablou indexat dupa noduri, fiecare intrare în tablou continând adresa listei nodurilor adiacente. Lista nodurilor adiacente poate fi dinamica sau statica. Pentru graful din fig.2.2.1, sunt prezentate:
matricea de adiacente în fig.2.2.2.;
lista de adiacente dinamica în fig.2.2.3.;
lista de adiacente statica în fig.2.2.4.
2.3.Explorarea în largime
Explorarea în largime consta în urmatoarele actiuni:
se trece într-o coada vida nodul de pornire;
se trece extrage din coada câte un nod care este prelucrat si se adauga toate nodurile adiacente lui neprelucrate. Se repeta acest pas pâna când coada devine vida.
Algoritmul este urmatorul:
void explorare_largime(int s)
/* s este nodul de pornire */
}
2.4.Explorarea in adâncime
La explorarea în adâncime se marcheaza vizitarea nodului initial, dupa care se viziteaza în adâncime, recursiv, fiecare nod adiacent. Dupa vizitarea tuturor nodurilor ce pot fi atinse din nodul de start, parcurgerea se considera încheiata. Daca ramân noduri nevizitate, se alege un nou nod si se repeta procedeul de mai sus.
Algoritmul este urmatorul:
void explorare_adancime(int s)
/* s este nodul de pornire* /
else pop(ST); /* se sterge nodul v din vârful stivei ST */
}
3.Mersul lucrarii
3.1. Pentru un graf orientat G =(V, E) si V' V sa se gaseasca subgraful indus G' =(V', E').Elementele din V si V' se citesc.
3.2. Sa se scrie câte o functie de construire pentru un graf G =(V, E), conform celor 3 reprezentari posibile.
3.3. Pentru un graf reprezentat prin matricea de adiacente, sa se implementeze algoritmii de traversare prezentati în paragrafele 2.3. si 2.4.
3.4. Sa se scrie o functie care sa verifice daca exista o cale între doua noduri date (v, w) ale unui graf orientat G =(V, E).
3.5. Pentru un graf neorientat dat G =(N, R), sa se scrie o functie care sa verifice daca graful este conex sau nu.
|