Scrieti programul C care va permite precizarea intre oricare doua noduri ale unui graf orientat dat existenta unui drum.
Descrierea algoritmului
Inchiderea tranzitiva a matricei unui graf
Stim ca un graf este complet definit daca se cunoaste 959f56j matricea de adiacenta Arce. In implementarea de mai jos vom presupune ca numarul de noduri ale grafului este fix, prin urmare graful este complet definit de matricea de adiacenta Arce. O expresie de forma Arce[i][k] && Arce[k][j] are valoarea true doar daca exista arc de la nodul i la nodul k si respective de la nodul k la nodul j .
Aceasta expresia va fi true daca exista un drum de lungime 2 de la nodul cu indexul i la nodul cu indexul j. Daca luam in considerare acest lucru o expresie de forma
(Arce[i][1]&&Arce[1][j])||(Arce[i][2] && Arce[2][j])||.||(Arce[i][NrNoduri]&& Arce[NrNoduri][j]) este true daca cel putin una din expresiile din paranteze este true, deci daca avem cel putin un drum de lungime 2 de la nodul i la nodul j.
Notam Arce2 produsul logic al matricei Arce cu ea insasi, deci Arce2[i][j] are valoarea true daca exista un drum de lungime 2 de la nodul i la nodul j.
Exemplu:
Fie graful de mai jos:
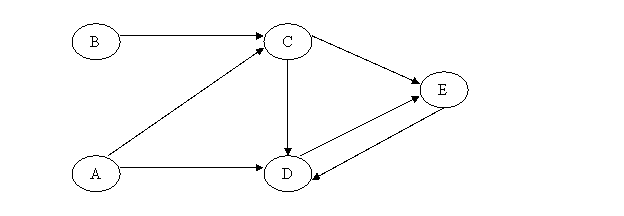
In mod analog determinam matricea Arce3 cu proprietatea ca Arce3[i][j]=true daca exista un drum de lungime 3 de la i la j , ca fiind produsul logic intre matricile Arce2 si Arce. Prin inductie matematica se constata ca matricea ArceNrNoduri ne va preciza daca exista un drum de la i la j de lungime NrNoduri.
Consideram o matrice Drum cu proprietatea ca Drum[i][j]=true daca exista un drum de la i la j de lungime mai mica sau egala cu NrNoduri.
Drum[i][j]=Arce[i][j] || Arce2[i][j] || …|| ArceNrNoduri[i][j]
Daca presupunem prin absurd ca ar exista un drum de lungime m>NrNoduri si fie acesta i,i1,i2,i3,…,im,j atunci pentru ca graful are doar NrNoduri exista cel putin un index k care apare de cel putin doua ori. Eliminand toate eventualele cicluri vom obtine in final un drum format din noduri distincte deci de lungime mai mica decat NrNoduri .
Avand in vedere formulele de calcul:
Drum=Drum+Arcek
Arcek=Arcek-1*Arce
si doua functii ajutatoare Atribuire si Produs vom putea calcula inchiderea tranzitiva
( matricea drumurilor) a matricei de adiacenta Arce.
Procedand in acest mod pana cand pe drum vor ramane doar noduri distincte vom obtine un drum sigur de lungime mai mica sau egala cu n.
Matricea drum astfel obtinuta se mai numeste inchidera tranzitiva a matricei de adiacenta.
In cazul in care numarul de noduri ale grafului este fix, ceea ce presupune ca vom putea adauga noi arce sau suprima in structura de date de tip graf, dar nu si noduri, atunci tipurile de date folosite si variabilele utilizate in prelucrarea structurii de tip graf cu varianta II 2 vor fi urmatoarele:
#define NrNoduri 5
typedef char TipCheie;
typedef TipCheie TipEl;
typedef TipEl TipTabEl[NrNoduri];
typedef int TipMatAdi[NrNoduri][NrNoduri];
typedef struct
Graf;
Graf g;
Pentru a calcula inchidera tranzitiva vom folosi o functie Inchidere Tranzitiva. Vom folosi si o functie Produs care va seta matricea C ca fiind produsul dintre A si B. Atribuie(a,b) care va realiza cea de-a doua matrice primei.
void InchTranz(TipMatAdi Adi, TipMatAdi Drum)
}/* InchTranz */
Rezolvare :
Scrieti programul C care va permite precizarea intre oricare doua noduri ale unui graf orientat dat existenta unui drum.
#include <graphics.h>
#include <stdlib.h>
#include <stdio.h>
#include <conio.h>
#include <ctype.h>
#include <math.h>
#define R 130
#define r 15
#define pi 3.1416
#define maxN 30
typedef char TipCheie;
typedef TipCheie TipEl;
typedef int TipContor;
typedef TipEl TipTabEl[maxN];
typedef int TipMatAdi[maxN][maxN];
typedef struct
Graf;
typedef struct
TipArc;
int n,k,x0,y0,xk,yk,i,j,x1,y1,x2,y2,a;
char s[2]=,c1,c2,c;
Graf g;
TipArc IndiceArc;
TipEl e;
TipMatAdi Adi,Drum;
int IndiceNod;
void Init_Mod_Grafic(void)
}//initmodgrafic
void DesenareNoduri(void)
}//DesenareNoduri
void DesenareGraf(void)
}//DesenareGraf
void Inser_Nod(Graf *g,TipEl e)
/*g->Arce[g->Contor-1][g->Contor-1]=1;*/
}/*Inser_Nod*/
void Inser_Arc(Graf *g,TipArc IndiceArc)
void Suprima_Nod(Graf *g, int IndiceNod)
g->Contor--;
} /* Suprima_Nod */
void Suprima_Arc(Graf *g,TipArc IndiceArc)
/*Suprima_Arc*/
int Cauta_Nod(Graf g,TipCheie Cheie)
//cauta nod
void Creare(void)
//crearea multimii arcelor
if(g.Contor==0)
printf('Nu exista noduri!n');
else
printf('Adaugi arc?(D/N)');
fflush(stdin);scanf('%c',&c);c=toupper(c);
}
}
}
}/*Creare*/
void Afisare_Matrice(TipMatAdi A)
}//AfisareMatrice
void TipMat(TipMatAdi a)
putchar('n');
}
void Produs(TipMatAdi a,TipMatAdi b,TipMatAdi c)
}//produs
void Atribuie(TipMatAdi a,TipMatAdi b)
/*Atribuie*/
void Inch_Tranz(TipMatAdi Adi,TipMatAdi Drum)
}/*Inchid_Tranz*/
int main(void)
}
DesenareGraf();
break;
case 'S': printf('Introduceti nodul de suprimat:');
fflush(stdin);scanf('%c',&e);e=toupper(e);
IndiceNod=Cauta_Nod(g,e);
if(IndiceNod!=-1)
Suprima_Nod(&g,IndiceNod);
else printf('Nodul nu exista in graf!n');
DesenareGraf();
break;
case 'D':if(g.Contor!=0)
}
else
printf('Graful este vid!n');
break;
case 'G': DesenareGraf();
break;
case 'M': Afisare_Matrice(g.Arce);
break;
case 'P': clrscr();
cleardevice();
printf('Matricea Drumurilor:nn');
Inch_Tranz(g.Arce,Drum);
TipMat(Drum);
break;
case 'E': break;
default : printf('Optiune gresita!n');
break;
}
printf('Tastati Enter!n');
fflush(stdin);
getch();
}
while(op!='E');
return 0;
}
|