Studiul complexitatii algoritmului Quick_Sort in caz mediu

Studiul complexitatii algoritmului Quick_Sort in caz mediu

Pentru complexitatea medie trebuie considerata probabilitatea tuturor aparitiilor datelor de intrare. Consideram ca orice configuratie de date la intrare este egal probabila. Probabilitatea ca pivotul sa fie plasat in pozitia k este egala pentru . Asadar, pivotul va fi plasat in pozitia k prin partitionare, cu o probabilitate egala cu 1/n, pentru .

Suma tuturor probabilitatilor este 1. Evenimentul este plasarea pivotului in pozitia k. Consideram T_i(n) timpul de executie al algoritmului Quick_Sort atunci cand pivotul este plasat in pozitia i:

Rezulta:   

Timpul mediu va fi o medie aritmetica:

Dezvoltand,

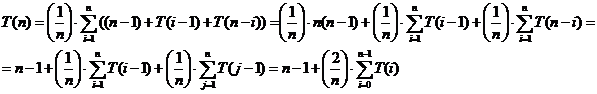
(Facand schimbarea de variabila j = n - i + 1)

Rezulta relatia de recurenta cu istorie completa:

Aceasta se rezolva astfel: inmultind relatia cu n rezulta:

Scriem acum relatia inlocuind pe n cu n+1:

Si scazandu-le acum membru cu membru rezulta:

care se inmulteste cu: ,

Notam:

Facand o majorare:   

(un element nu se ordoneaza).

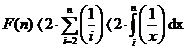Rezulta:    si este aria zonei de sub graficul functiei .

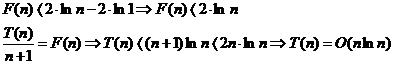
unde O(n ln n) este complexitatea acestei functii.