Lectia 17 Exercitii bancare

Scopul lectiei

Explicarea terminologiei folosite în limbajul curent comparativ cu cea folosita de EXCEL

Exista diferente între limbajul folosit de marele public si cel folosit în domeniul bancar american care a fost preluat de EXCEL.

Noi prin rata întelegem suma ce o vom plati lunar. EXCEL-ul întelege dobânda.

NODEX al limbii române contine urmatoarea definitie:

anuitate = Suma de bani (incluzând o parte din capital si dobânda corespunzatoare) care se plateste periodic (de obicei anual) pentru a rambursa un capital sau o datorie.

Din punct de vedre al EXCEL-ului:

Anuitate reprezinta întregul capital si dobânda aferenta, daca si numai daca, toate platile sunt egale si efectuate la intervale egale.

Se vorbeste de anuitate anuala (ceea ce este un pleonasm pentru ca anuitate de fapt înseamna plati anuale de unde îi vine si numele), pentru ca si atunci într-adevar este "o parte din capital si dobânda corespunzatoare" aferenta unui an, altfel vorbim de întregul capital si de întreaga dobânda aferenta capitalului împrumutat. Prin Help gasiti notiunea de anuitate cu întelesul de plata întregului capital si a dobânzii aferente.

Fig 17.1 (Un mic exemplu de echivalenta a termenilor)

Când iau un împrumut,

valoarea prezenta Pv este chiar împrumutul (este valoarea actualizata sau suma totala pe care o valoreaza în prezent o serie de plati viitoare) se mai numeste si capital de baza, iar

valoarea viitoare Fv este 0 (ea este suma la care se va ajunge dupa efectuarea tuturor platilor si pentru un împrumut este 0 - zero - , pentru ca trebuie sa îl achitam integral)

Când depun bani la banca pentru a face un depozit, adica fac o investitie, este invers:

Pv = 0 fiindca nu am nici un capital de baza si

Fv este depozitul pe care îl am în vedere sau investitia pe care doresc sa o fac pe parcursul a mai multor perioade de timp (luni, trimestre, ani), depinde cum fac platile, adica în ce ritm depun banii.

Functia PMT arata asa =PMT(rate;nper;pv;fv;type) argumentele subliniate sunt obligatorii

În consecinta propun urmatorul dictionar ad-hoc:

Fig 17.2

Doresc un împrumut (Calculul ratei lunare)

Eu sunt debitorul, Banca este creditorul.

Banca aplica

dobânda de 10% pe an si

perioada pentru care îmi acorda împrumutul este de 10 ani.

Sunt 2 aspecte:

stiu suma pe care o doresc si vreau sa aflu rata lunara ce o voi plati.

De la început stiu ca nu pot plati o rata mai mare de "atât" si vreau sa stiu ce împrumut îmi va acorda banca.

Cum se apeleaza functia PMT - vreau sa aflu rata lunara ce o voi plati-

Apelati iconita  iar daca nu este pe ecran (ca la WINDOWS XP) apelati sau procedati ca în Fig 17.3.

Înserare Functie si apare Lipire functie. Cautati functia PMT clic pe ea ti clic pe OK si apare Fig 17.4.

Fig 17.3 (Apelarea functiilor si alegerea uneia dintre ele)

Fig 17.4 (Apelare functiei PMT)

Daca iau acel împrumut platesc pe luna 132,15 RON. Dobânda este pe an si se împarte la 12 sa rezulte dobânda lunara. Nr. perioadelor sunt numarul lunilor deci nr.ani x 12.

Cum se apeleaza functia PV - sa aflu cât pot împrumuta-

Ma gasesc în situatia cealalta când stiu ca nu pot plati mai mult de 132,15 RON. Ce suma îmi împrumuta banca? Dban = dobânda bancii.

Cum apar parametri pe ecran în timpul apelarii functiei PMT

Cu alte cuvinte nu este tot una daca la un împrumut pe 10 ani cu plata anuala a ratelor, plata unei rate o fac în 3 ianuarie sau în 30 decembrie. Vezi Fig 17.6. Exista diferente.

Comparatia dintre functiile PMT si FV arata ca se obtin aceleasi rezultate.

Fig 17.6 (Ratele sunt anuale!)

Nu conteaza cu ce formula calculati constituirea unui depozit, conteaza când se face plata! Exista o mare diferenta între a lua un împrumut si a face o investitie. În cazul unui împrumut de 10.000 lei (RON) rata anuala este de 1627,45 RON. Dar numai 627,45 RON sunt necesari ca rata anuala pentru a constitui un depozit egal cu împrumutul de care vorbeam.

Plata la începutul anului (tipul, felul platii = 1) de asemenea are importanta, micsoreaza rata anuala. Acelasi lucru se va întâmpla si daca exista o alta periodicitate a platiilor. Cu cât platile sunt mai dese cu atât anuitatea ca suma a valorii împrumutului si a valorii dobânzii aferente, este mai mica.

Fig 17.7 (Suma platilor anuale scade pe masura ce se platesc mai des ratele)

Cât costa un împrumut

Un imprumut costa cu atît mai mult

cu cât rata este mai mare si perioada mai lunga.

Costul unui imprumut este diferenta dintre :

Pentru exemplificare am ales un mprumut cu rate lunare care costa mai putin. Urmariti Fig 17.8. Din tabelul corespunzator se poate alege o varianta de împrumut.

În concluzie iau un împrumut pe 10 ani de 10.000 lei si platesc 15.201, daca dobânda anuala este de 10%. Diferenta este costul împrumutului. Costul anual al împrumutului este de 520,10 lei/an sau 43,34 lei/luna.

Atentie:

În realitate rata nu cuprinde numai suma împrumutata plus dobânda aferenta, ci o serie de taxe si comisioane care în final fac ca un împrumut anuntat ca are o dobânda anuala de 10%, de fapt dobânda anuala sa fie de 12 - 14%. Aici discutam numai de anuitatea pura, negrevata de alte taxe si comisioane.

Când e vorba de rata lunara dobânda se împarte la 12 pentru a lua în calcul dobânda pe luna nu pe an, iar perioada este nu numarul anilor ci cu numarul lunilor.

Când e vorba de rata anuala nu se mai fac operatiile de mai sus.

Cum se constituie un depozit bancar

Daca se depune 132,15 lei lunar, cu o dobânda anuala de 10% timp de 10 ani, în final depozitul va fi de 27.070 lei

Functia este FV. Sa nu se confunde cu parametrul "fv" care înseamna "viitoare valoare".

=FV(rate;nper;mpt) - forma scurta.

Valoarea depozitului se poate calcula prin formule create de utilizator (calcul manual). Este incomod pentru ca trebuie sa folosim 120 de rânduri câte luni sunt în 10 ani. Fig 17.12. dar nu este imposibil.

Fig 17.12 (Calculul manual al acumularii depozitului bancar)

Ideea este ca aplic procentul dobânzii la ce exista depus si adaug noua rata.

Adica[3]:

399,76 = 265,40 x 0,10/12 + 265,40 + 132,15 sau dând factor comun avem:

399,76 = 265,40 x (1 + 0,0083333) + 132,15 adica 399,76 = 265,40 x 1,008333 + 132,15

Prin acest calcul iterativ, am rezolvat problema fara a sti cum se calculeaza dobânda compusa.

De remarcat urmatorul lucru:

Daca iau un împrumut de 10.000 lei pe 10 ani cu dobânda de 10% platesc lunar 132,15 lei si în final 15.201 lei. Banca îmi adauga la împrumut 5.201 lei prin dobânzile pe care mi le percepe.

Daca depun lunar suma tot de 132.15 lei cu aceiasi dobânda pe timp de 10 ani, depozitul bancar va fi 27.070,26 lei si de fapt am depus 132,15 lei/luna x 120 luni = 15.858 lei., iar banca îmi mai adauga din dobânzi înca 11,212 lei.

Datorita acestui lucru bancile la împrumuturi cer o dobânda anuala mai mare, decât se acorda la depozite.

Verificari

Functia EFFECT întoarce dobânda reala a împrumutului.

Prin aceasta functie verificam dobânda reala. În calculul ratelor ce le platim periodic se fac unele aproximari si rezulta o rata putin mai mare datorita rotunjirilor.

Functia EFFECT() reface calculul invers. Se afla astfel dobânda reala. Diferentele sunt mai mici de 1%. Calculul ratei se face introducând unele rotunjiri. Se ajunge la o suma 132.15 lei care si ea este rotunjita. Este normal ca lucrurile sa nu fie tocmai exacte. Deci dobânda reala este 10,51%. În fond nu prea are importanta. Conteaza rata ce este platita periodic.

Toate functiile prezentate ca si celelalte au aceiasi caseta de stabilire a parametrilor (argumentelor). Caseta aceasta permite multe simulari.

Rezultatul final rotunjit nu apare "din prima". Se face clic pe OK si apoi se apeleaza din nou functia si asa apare Fig 17.15.

Când se fac evaluari nu este nevoie de rezultate rotunjite.

O alta formula de calcul a anuitatii

n exemplul de mai jos Fig 17.16 este vorba de anuitatea anuala.

Semnul (caciula lui â) înseamna ridicare la putere. ani este exponent.

înseamna 2 la puterea 5 adica 2⁵.

Semnului i se mai spune caret! În engleza am gasit ca înseamna semn de omisiune.

Daca va fi vorba de plati lunare situatia se schimba. Dobânda anuala a bancii se împarte la 12 iar durata se înmulteste cu 12, asa cum este în Fig 17.16 bis.

Ce facem când nu avem conditii de anuitate

Tot ce am învatat pâna acum sunt functii care presupun conditii de anuitate, dobânda constanta si rate egale la intervale egale.

Exista situatii când platile nu sunt egale, chiar daca perioadele sunt egale.

Exemplu: S-a încheiat o asigurare de viata. Prima trimestriala este de 150 RON. Asiguratul accepta marirea anuala a acestei prime în functie de inflatie. În consecinta va plati în fiecare an mai mult, prima va fi din ce în ce mai mare.

Recunosc ca în Fig 17.17 sunt lucruri mai complicate. Sunt necesare explicatii.

Asiguratul îsi face urmatoarea socoteala. Daca as depune trimestrial la o banca suma ce o platesc drept rata de asigurare, în final ce depozit as avea? Urmariti Fig 17.17 si comentariile.

Din tabelul de mai sus, nu se pot trage decât concluzii relative, nu sigure. Formarea depozitului nu este întotdeauna mai buna decât contractarea unei asigurari de viata. Societatile de asigurari garanteaza o suma minima, cam de 9.000 RON în conditiile de mai sus si de aproximativ 21.000 RON prin "participare la beneficii". Daca asiguratul moare dupa 5 ani, urmasii lui primesc minim 9.000 RON, depozitul creat în 5 ani nu cred ca depaseste 4.000 RON .

În cazul de mai sus nu avem o anuitate. Totusi daca formulam într-un anume fel problema o putem rezolva cu functii create expres pentru rezolvarea numai a anuitatilor. În exemplul de mai sus sunt 14 anuitatii! Coloanele F si G din Fig 17.17

Fig 17.18 (Câteva din cele 15 plati în conditii de anuitate)

Eu sunt partizanul asigurarilor. Nici un cutremur nu m-a prins neasigurat!

Consider interesanta modalitatea de calcul a constituirii unui depozit virtual, prin depuneri succesive. Cu alte cuvinte suma de 150 RON va fi depusa pe 15 ani, suma de 10,85 RON pe 14 ani, s.a.m.d. ca în Fig 17.19.

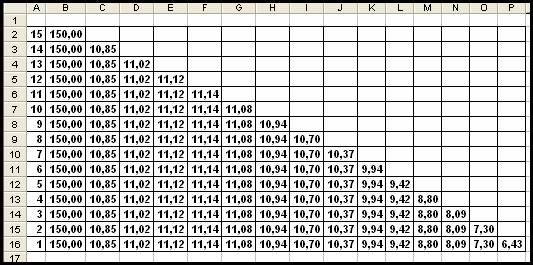
Fig 17.19 (Desfasuratorul celor 15 depuneri pe perioade diferite)

Ce înseamna o investitie

Putina lume stie ce înseamna cu adevarat "time is money". Raspunsul ca timpul înseamna bani este stupid. Un pensionar sau un somer au timp berechet. Asta înseamna ca au si bani, asa automat, din multul timp pe care îl au la dispozitie? Este vorba de Pretul-timp al banilor, adica o suma de bani primita astazi înseamna (valoreaza) mai mult decât aceiasi suma primita în viitor!

Fig 17.21 (Desfasuratorul depunerilor lunare)

Fig 17.22 (O singura depunere initiala)

Fig 17.23 (Desfasuratorul depunerii unice la începutul perioadei)

Acum sa comparam rezultatele simularii noastre:

Fig 17.24 (Dobânda este aceiasi 10%)

Am facut ipoteza ca eu nu pot plati mai mult pe luna de 132,15 lei (RON) asadar nu pot sa iau un împrumut mai mare de 10.000 lei. Nu-l mai iau! Dar daca nu iau împrumutul si tot pot economisii pe luna 132,15 lei, depunând lunar acesti bani, pot forma în 10 ani un depozit de 27.070 lei. În total treaba aceasta ma costa 15.858 lei.

Daca depun la început suma de 10.000 lei (ca la CEC), dupa 10 ani am un depozit de 25.937 lei. Mai putin cu 1.133 lei, (27.070 - 25.937 = 1.133), dar si am depus mai putin. (15.858-10.000) lei. Una peste alta sunt în câstig 5.858 - 1.133 = 4.725 lei.

Daca aveam cei 15.858 lei de la început si îi depuneam, depozitul meu ajungea la 41.132 lei. (Daca!)

Acesta e pretul-timp al banilor.