Proiect de cercetare stiintifica - retele petri

Retele

  X(cauza) Y(efect)

Intrare     Iesire

Stare

Retelele (grafurile) propuse de Petri (1962) descriu, folosind principiile algebrei boolene, evolutia unui vector de elemente naturale, avand semnificatia de stare, fara precizarea momentelor efective de timp cand aveau loc modificarile starii.

Petri a modelat sistemele parale si distribuite astfel:

prin divizarea starii sistemului in elemente care sa caracterizeze starile locale ale subsistemelor constituente, un element putand face parte din mai multe stari locale;

prin caracterizarea evolutiei sistemului pe baza concurentei unor tranzitii locale;

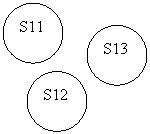
Aceste sisteme tranzitionale concurente au fost denumite RETELE PETRI (fig. 2).

FIG. 2

S1.Sn = stari ale automatului(sistemului);

S11S1n= stari ale subsistemului 1;

Ulterior (1980) sau introdus informatii temporale si au rezultat Retele Petri temporizate (care permit studii cantitative) si netemporizate (care permit studii calitative). Astfel Retelele Petri pot modela fenomene specifice sistemelor cu evenimente discrete, modelari formulate atat in context temporizat cat si netemporizat cum ar fi:

-succesiunea (o stare succede altei stari);

-conflictul (selectare unei posibilitati);

-congrunta (evolutii paralele);

-sincronizarea (incheierea unor evoutii paralele);

-excluderea (conditionare reciproca a unor stari);

STRUCTURA RETELELOR PETRI

O retea Petri(fig. 3) se compune dintr-un graf notat N si o stare initiala denumita marcaj initial. Graful N al retelei este orientat, ponderat si bipartit spunem despre un graf ca este bipartit daca putem imparti nodurile in doua multimi disjuncte, astfel incat nu exista muchii care sa lege noduri din aceeasi multime), constand in doua tipuri de noduri:

- pozitii (locatii), P(i) cu i=1,n;

- tranzitii, T(j) cu j=1,m;

Arcele orientate unesc o pozitie cu o tranzitie sau o tranzitie cu o pozitie si sunt unidirectionale. O pozitie si o tranzitie pot fi legate prin cel mult un arc.

Daca un arc leaga o tranzitie T_j de un loc P_i, atunci arcul este reprezentat prin perechea (T_j, P_i) si se spune ca T_j este o tranzitie de intrare in locul P_i iar P_i este un loc de iesire din tranzitia T_j. Analog, daca un arc leaga un loc P_i de o tranzitie T_j, atunci arcul este reprezentat printr-o pereche (P_i, T_j) si se spune ca locul P_i este un loc de intrare in tranzitia T_j iar tranzitia P_j este o tranzitie de iesire din locul P_i.

FIG. 3

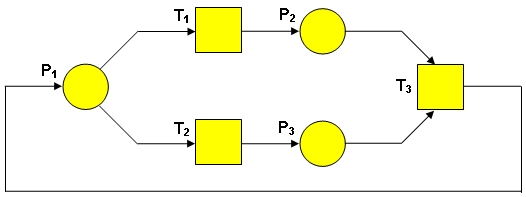
In exemplul de retea Petri din figura de mai sus:
- locul P₁ este loc de iesire din tranzitia T₃ si este loc de intrare tranzitiile T₁ si T₂ -tranzitia T₁ este tranzitie de iesire din locul P₁ si este tranzitie de intrare in locul P₂

Prin evaluarea arcelor unei retele Petri se intelege o aplicatie prin care fiecarui arc al retelei i se ataseaza o valoare naturala. Daca un arc leaga un loc P_i de o tranzitie T_j, atunci evaluarea arcului respectiv se noteaza cu a(P_i, T_j), iar daca un arc leaga o tranzitie T_j de un loc P_i atunci evaluarea sa se noteaza cu a(T_j, P_i).

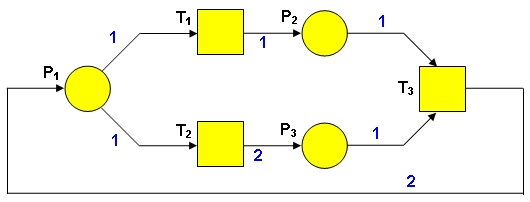
FIG. 4

In exemplul de retea Petri din figura de mai sus, toate arcele au evaluare unitara, cu exceptia arcelor de la T₂ la P₃ si de la T₃ la P₁, care au evaluarea 2:
a(P₁, T₁) = a(P₁, T₂) = a(T₁, P₂) = a(P₂, T₃) = a(P₃, T₃) = 1;
- a(T₂, P₃) = a(T₃, P₂) = 2.

Matricea care contine evaluarile arcelor unei retele Petri este denumita matricea de incidenta. Elementul de pe linia i si coloana j a matricei de incidenta A are valoarea evaluarii arcului ce leaga nodul P_i de tranzitia T_j daca T_j este o tranzitie de intrare in nodul P_i. Daca tranzitia T_j este o tranzitie de iesire din nodul P_i, atunci elementul respectiv al matricei A are aceeasi valoare a evaluarii arcului corespunzator, dar cu semn schimbat. Daca intre nodul P_i si tranzitia T_j nu exista nici un arc, atunci elementul corespunzator al matricei de incidenta este nul. Matricea de incidenta a retelei din figura de mai sus este:

-elementele a_2,2 si a_3,1 au valori nule deoarece intre locul P₂ si tranzitia T₂, sau intre locul P₃ si tranzitia T₁ nu exista nici un arc;
-elementele a_1,1, a_1,2, a_2,3 si a_3,3 au valori negative deoarece tranzitiile corespunzatoare sunt tranzitii de iesire (T₁ si T₂ sunt tranzitii de iesire din P₁, T₃ este tranzitie de iesire din P₂ si P₃).

Prin marcajul unei retele Petri se intelege o aplicatie care asociaza fiecarui loc din retea un numar intreg reprezentat prin tot atatea puncte (jetoane) in interiorul cercului care simbolizeaza locul respectiv. Nu orice retea Petri trebuie sa posede un marcaj. Cele care au atasata aplicatia respectiva se numesc retele Petri marcate

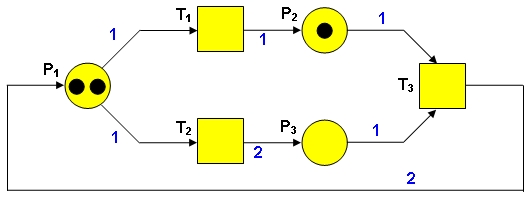
FIG. 5

Marcajul retelei din figura de mai sus este M = (2, 1, 0), deoarece locul P₁ contine 2 jetoane, locul P₂ contine un jeton iar locul P₃ nu contine nici un jeton.

RETELE PETRI NETEMPORIZATE

Marcajul unei retele Petri se poate modifica in conformitate cu regulile de tranzitie (validare si executare):

o tranzitie este validata daca fiecare pozitie p de intrare in tranzitia t este marcata cu cel putin W(p,t) jetoane;

o tranzitie validata poate sa fie sau nu declansata dupa cum evenimentul asociat are loc sau nu;

executarea unei tranzitii validate indeparteaza W(p,t) jetoane din pozitia p de intrare a lui t si adauga W(t,p) jetoane in pozitia p de iesire a lui t.

pozitii pozitii

intrare iesire

tranzitii de intrare tranzitii de iesire FIG. 6

O tranzitie fara nici o pozitie de intrare se numeste tranzitie sursa. Aceasta este validata neconditionat (fara a fi obligatoriu sa se execute) si executarea ei produce jetoane. O tranzitie fara nici o pozitie de iesire se numeste tranzitie receptor iar executarea ei consuma jetoane.

In cazul unei retele Petri netemporizata se presupune ca executarea unei tranzitii nu consuma timp si ca jetoanele pot ramane in pozitii pentru orice durata de timp. Deoarece executarea unei tranzitii se petrece instantaneu, tranzitiile se executa numai secvential. Aceste presupuneri fac ca modelul de retea Petri netemporizata sa fie folosit numai pentru studierea proprietatilor logice, calitative care nu depind de timp.

Pentru regula de validare a unei tranzitii prezentata anterior s-a presupus ca fiecare pozitie are capacitate infinita. In modelarea sistemelor fizice este firesc a considera o limita superioara a numarului de jetoane pe care il poate contine fiecare pozitie, asociind fiecarei pozitii p capacitatea sa, notata K(p) definita ca numarul maxim de jetoane ce pot fi continute in p . O astfel de retea se numeste cu capacitate finita.

Intr-o retea cu capacitate finita, pentru validarea unei tranzitii t este necesara urmatoarea conditie suplimentara: numarul de jetoane in fiecare pozitie de iesire p a lui t nu poate sa depaseasca capacitatea pozitiei respective, K(p), atunci cand t s-ar executa. In acest caz, regula tranzitiei se va numi regula stricta a tranzitiei spre a o deosebi de cea enuntata anterior care mai este uneori referita drept regula simpla a tranzitiei.

Proprietatile comportamentale ale retelelor Petri netemporizate sunt dependente atat de topologia cat si de marcajul initial al retelei. In timp ce proprietatile structurale iau in considerare numai topologia retelei, fiind independente de marcajul initial al acesteia.

A.) PROPRIETATI COMPORTAMENTALE

Accesibilitate

O secventa de executari de tranzitii ale unei retele Petri conduce la modificarea marcajului (a distributiei de jetoane), in conformitate cu aplicarea regulii tranzitiei. Despre un marcaj M_n se spune ca este accesibil din marcajul initial M₀ daca exista o secventa de executari de tranzitii care transforma M₀ in M_n. Faptul ca marcajul M_n este accesibil din M₀ prin secventa de executari a se noteaza M₀[a >M_n.

Multimea tuturor marcajelor care pot fi atinse in reteaua N pornind din marcajul initial M₀ se noteaza prin R(N, M₀). Multimea tuturor secventelor de executare posibile in reteaua N pornind din marcajul initial M₀ se noteaza prin L(N, M₀)

2. Marginire

O retea Petri cu capacitate nelimitata este k-marginita sau, in limbaj prescurtat, marginita daca numarul de jetoane din fiecare pozitie nu depaseste un numar finit k pentru orice marcaj accesibil din marcajul initial M₀ (adica pentru orice secventa de executari de tranzitii pornind de la M₀). In limbaj matematic, aceasta revine la:

M(p) < k pentru orice p din P si orice M din R(M₀).

Din punct de vedere practic, cand reteaua modeleaza un proces, proprietatea de marginire permite studierea eventualelor depasiri ale unor capacitati fizice de procesare / memorare a informatiei sau de prelucrare stocare a produselor. Marginirea asigura nedepasirea anumitor valori, indiferent de secventa de evenimente (adica tranzitii).

3. Viabilitate

O retea Petri (N, M₀ ) se numeste viabila daca, indiferent de marcajul care a fost atins pornind din M₀, este posibil ca, in continuare, sa fie executata orice tranzitie t a retelei. Pana la executarea lui t poate fi necesara, eventual, executarea unui numar finit de alte tranzitii. Un marcaj pentru care nicio tranzitie a retelei nu mai poate fi executata se numeste deadlock. In baza definitiei viabilitatii se constata ca o retea viabila opereaza fara deadlock. Pe de alta parte, o retea care nu este viabila, nu evolueaza in mod obligatoriu catre deadlock, in sensul ca, pe langa tranzitia sau tranzitiile care nu mai pot fi executate, una sau mai multe tranzitii sunt executabile de o infinitate de ori. Intr-un atare caz se poate vorbi despre un deadlock partial.

Din punct de vedere practic, cand reteaua modeleaza un proces, proprietatea de viabilitate permite studiul functional fara incidente nereparabile (de factura logica, adica nu defecte), care sa necesite o interventie externa procesului Pe de alta parte, in cazul bazelor de date, un deadlock este un blocaj general la nivelul sistemului, in care tranzactiile ( operatiuni de citire - scriere) astepta unele dupa altele eliberarea blocarilor anterioare la nivelul inregistrarii respective. Daca apare o astfel de situatie SGBD-ul detecteaza si inlatura blocajul prin alegerea unei tranzactii ca victima si anularea ei prin rollback.

3. Reversibilitate

O retea Petri (N,M₀) se spune ca este reversibila daca pentru orice marcaj M din R(M₀), marcajul initial M₀ este, la randul sau, accesibil cand se porneste din M. Astfel, intr-o retea reversibila este intotdeauna posibila intoarcerea la marcajul initial. Din punct de vedere practic, cand reteaua modeleaza un proces, proprietatea de reversibilitate permite studiul repetabilitatii desfasurarii anumitor activitati sau a aparitiei anumitor conditii.

Observatie: Marginirea, viabilitatea si reversibilitatea sunt proprietati independente una de cealalta.

B.) PROPRIETATI STRUCTURALE

Proprietatile structurale ale retelelor Petri netemporizate depind numai de topologia retelei si nu depind de marcajul initial intr-unul din sensurile urmatoare:

fie proprietatea se pastreaza indiferent de marcajul initial;

fie proprietatea se refera la faptul ca exista marcaje initiate care asigura anumite secvente de executari de tranzitii.

Aceasta dependenta numai de topologie face ca tehnicile de analiza a proprietatilor structurale sa utilizeze instrumente specifice algebrei liniare care exploateaza proprietatile matricei de incidenta.

In cele ce urmeaza, Z^m(R^m) si Z^nxm , pentru n,m din N* , reprezinta multimea vectorilor coloana cu m elemente numere intregi (reale), respectiv cea a matricelor de dimensiune n x m cu elemente numere intregi. Vectorul cu toate elementele nule se noteaza cu 0.

Fie x si y doi vectori din Z. Vectorii x si y se definesc astfel

x=[x1,x2,……………..xn];

y=[y1,y2,……………..yn];

In continuare vom utiliza urmatoarea notatie de tip inegalitate:

x<y     xi<yi, i=1,m;

1. Marginire structurala

O retea Petri cu marcajul initial M₀ este structural marginita daca este marginita (in sens comportamental) pentru orice marcaj initial finit. Se spune ca o pozitie p a unei retele Petri este structural nemarginita daca exista un marcaj initial M₀ si o secventa de executari de tranzitii a pornind din M₀ astfel incat continutul in jetoane al pozitiei sa devina nemarginit.

2. Conservativitate

O retea Petri N este conservativa daca exista cate un intreg pozitiv y(p) pentru fiecare pozitie p, astfel incat pentru orice marcaj initial M₀ fixat si orice marcaj accesibil din M₀ M din R(M₀), are loc egalitatea:

M(y) = M₀ y)(= constant).

3. Repetitivitate

O retea Petri N este repetitiva daca exista un marcaj initial M₀ si o secventa de executari de tranzitii a ce porneste din M₀, astfel incat orice tranzitie apare infinit de des in a. Se spune ca o retea Petri N este partial repetitiva daca exista un marcaj initial M₀ si o secventa de executari de tranzitii a ce porneste din M₀, astfel incat o parte din tranzitii (in sensul ca nu toate tranzitiile) apar infinit de des in a.

4. Consistenta

O retea Petri este consistenta daca exista un marcaj M₀ si o secventa de executari de tranzitii a de la M₀ inapoi la M₀, astfel incat fiecare tranzitie apare cel putin o data in a.

RETELE PETRI CU TEMPORIZARE DETERMINISTA

1. Retele cu tranzitii temporizate

O retea Petri este cu tranzitii temporizate sau temporizata T, daca fiecare tranzitie t(i), i=l … n; are asociat un interval de timp d(i)>0, prin intermediul unei functii de temporizare tip T (tranzitie). In ceea ce priveste functionarea retelei Petri temporizate T, intervalele de timp d(i)>0 joaca rolul unor intarzieri ce se manifesta dupa cum urmeaza: din momentul cand tranzitia t este validata, un numar de a(i,j) jetoane vor ramane rezervate (nedisponibile din punctul de vedere calitativ, logic, al aplicarii regulii tranzitiei) in pozitia p(i) care precede tranzitia t(i) pentru d(i) unitati de timp, inainte de deplasarea lor prin executarea tranzitiei t(i) Reamintim ca a(i, j) este ponderea arcului de la pozitia p(i) la tranzitia t(i), fiind elementul generic al matricei de incidenta de intrare A. In cazul a doua sau mai multe tranzitii aflate in conflict, selectarea tranzitiei care se va executa se realizeaza pe baza unui mecanism de prioritati sau probabilitati asignate respectivelor tranzitii. Atragem atentia asupra faptului ca duratele de timp asociate tranzitiilor nu joaca nici un rol in rezolvarea situatiilor conflictuale, in sensul ca nu este obligatoriu sa se execute tranzitia corespunzatoare celei mai mici durate de timp.

2. Retele cu pozitii temporizate

O retea Petri este cu pozitii temporizate, sau temporizata P, daca fiecarei pozitii p(j), j= 1..m, i se asociaza un interval de timp d(j)>0, prin intermediul unei functii de temporizare tip P (pozitie). Retelele temporizate P se folosesc pentru a introduce in modelul matematic informatiile privitoare la durata activitatilor, elaborand, astfel, un model cantitativ. Cu ajutorul unui asemenea model se pot lua in discutie toate caracteristicile temporale specifice sosirii clientilor si servirii acestora cu anumite succesiuni de operatii de catre resursele sistemului.

In cazul unui model ce reprezinta o structura de conducere a unui sistem cu evenimente discrete, fiecarei pozitii asociate unei operatii i se asigneaza durata activitatii de servire (procesare), iar fiecarei pozitii asociate unei resurse (registri de memorie) i se asigneaza durata activitatii de eliberare a resursei.

RETELE PETRI CU TEMPORIZARE STOHASTICA

Daca duratele de timp asignate tranzitiilor (pozitiilor) unei retele Petri cu temporizare T (sau P) au valori aleatoare, reteaua respectiva este cu temporizare stohastica. In situatia in care reteaua Petri modeleaza un sistem fizic, este natural ca durata de timp asignata unei tranzitii (pozitii) ce reprezinta o operatie, respecta o anumita distributie de probabilitate. In acest mod, fiecarei tranzitii (pozitii) temporizate ii este asociata distributia de probabilitate corespunzatoare duratei de timp asignate. O retea cu temporizare determinista poate fi privita drept un caz particular de retea cu temporizare stohastica (corespunzatoare distributiei constante).

Subliniem faptul ca duratele de timp asociate tranzitiilor nu joaca nici un rol in rezolvarea situatiilor conflictuale, spre deosebire de cazul retelelor Petri stohastice. In cazul a doua sau mai multe tranzitii aflate in conflict intr-o retea Petri cu temporizare T stohastica, selectarea tranzitiei t(i) care urmeaza sa se execute se realizeaza pe baza mecanismului de prioritati sau probabilitati asignate respectivelor tranzitii (similar principiului prezentat in contextul retelelor cu temporizare T determinista). Apoi se genereaza durata de timp corespunzatoare legii de repartitie asociata tranzitiei t(i) selectate. Aceasta durata reprezinta intarzierea manifestata din momentul cand tranzitia este validata pana la executarea acesteia.

In general, modelarea unui sistem fizic printr-o retea Petri cu temporizare stohastica se realizeaza in scopul evaluarii performantelor de regim permanent ale sistemului, presupunand ca se poate estima ,,comportarea medie' a sistemului pe baza observarii (simularii) modelului pe un interval de timp suficient de lung. Aceasta presupunere implica proprietatile modelului: la limita, atunci cand intervalul de observare (simulare) tinde la infinit, estimarile valorilor medii ale indicilor de performanta studiati (de interes) tind aproape sigur la valorile medii teoretice. Astfel, performantele sistemului fizic se pot estima pe baza analizei a doua procese stohastice asociate modelului de tip retea Petri cu temporizare stohastica, si anume procesul de executare a tranzitiilor si cel de marcaj. De regula, se presupune ca aceste doua procese stohastice sunt ergodice. Un ansamblu este numit ergodic daca cele doua tipuri de statistici (al tranzitiilor si marcajelor) coincid. Astfel pe baza modelelor de tip retea Petri cu temporizare stohastica se pot analiza performantele sistemelor fizice modelate (gradele de utilizare a resurselor, numar mediu de clienti serviti in unitatea de timp, duratele medii ale ciclurilor de productie, etc.).

O retea Petri se numeste stohastica (SPN) daca fiecarei tranzitii t ii este asociata o variabila aleatoare X_t de distributie exponentiala, care exprima intarzierea din momentul validarii pana la executarea tranzitiei Spre deosebire de retelele Petri cu temporizare T stohastica, daca la un moment dat intr-o retea Petri stohastica mai multe tranzitii sunt simultan validate, se va executa mai intai acea tranzitie care poseda intarzierea cea mai scurta. Astfel, intr-o SPN, nu are sens asignarea de probabilitati sau prioritati de executare pentru tranzitiile aflate in conflict. Intr-o SPN nu exista marcaje rezervate. Problema alegerii urmatoarei tranzitii care se va executa se pune de fiecare data cand marcajul retelei stohastice se modifica. Conflictele se rezolva in mod natural, prin generarea duratelor corespunzatoare tuturor tranzitiilor validate la momentul respectiv si selectarea acelei tranzitii careia ii corespunde cea mai mica durata.

Arbori de acoperire/accesibilitate

Fiind data o retea Petri (N, M₀), pornind de la marcajul initial M₀, modificarea marcajelor ca urmare a executarii tranzitiilor poate fi reprezentata sub forma unui arbore, denumit arbore de acoperire. In acest arbore, M₀ este radacina, iar marcajele generate sunt noduri; fiecare arc corespunde executarii unei tranzitii care transforma marcajul asociat nodului de plecare in marcajul asociat nodului de sosire.

In cazul unei retele Petri marginite, arborele de acoperire se numeste arbore de accesibilitate, deoarece poate cuprinde toate marcajele accesibile pornind din marcajul initial M₀ (care sunt in numar finit). In aceasta situatie, arborele de accesibilitate poate fi utilizat pentru studierea tuturor proprietatilor comportamentale. Un posibil dezavantaj il constituie numarul mare de noduri ce poate rezulta in arborele de accesibilitate, ca urmare a complexitatii retelei Petri studiate.

In cazul retelelor Petri nemarginite, arborele de acoperire va creste la nesfarsit. Pentru a pastra finititudinea reprezentarii de tip arbore de acoperire, se introduce un simbol special (ω) care poate lua valori oricat de mari.

Observatie: In cazul retelelor nemarginite, studierea proprietatii de viabilitate cu ajutorul arborelui de acoperire nu este intotdeauna posibila. Acest fapt se datoreaza pierderii (prin utilizarea simbolului ω) unor informatii numerice concrete, referitoare la marcajul pozitiilor nemarginite (de exemplu cresterea sau descresterea marcajului).

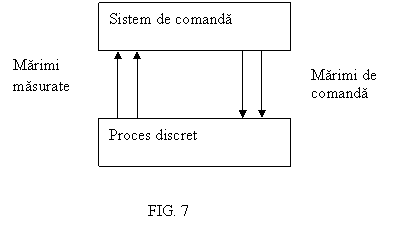
APLICATII ALE RETELELOR PETRI

Retelele Petri se utilizeaza pentru reprezentarea si descrierea modelelor pentru procese discrete, definite prin comenzi secventiale. In fig.7 se prezinta structura unui sistem de comanda discreta a unui proces, unde sunt mentionate marimile masurate si marimile de comanda. Comportarea dinamica a unui sistem discret este definita de derularea in timp si de intercalarea evenimentelor.

In conducerea proceselor, in multe cazuri, operatorul uman trebuie sa raspunda la semnale de alarma prin comenzi manuale, ceea ce este dificil in cazul unor procese de mare complexitate. Cu autorul retelelor Petri fuzzy (RPF ) experienta operatorului poate fi modelata si folosita in conducerea proceselor, in timp real. RPF modeleaza cunostintele si experienta expertului in conducerea unui proces, prin noduri si tranzitii in conceptul de conducere.

O retea Petri fuzzy ( RPF ) este compusa din noduri si tranzitii, obtinute dintr-o retea Petri normala. Nodurile si tranzitiile sunt fuzifixate in multimi fuzzy. Functia prin elementele sale reconstruieste caracteristicile si comportarea dorita a procesului. Intr-o retea se pot introduce limite, ca de exemplu debit maxim sau minim, dar si limitari dinamice, ca de exemplu viteza de deschidere a unei electrovalve.

Ideea de multime fuzzy (multime vaga) a fost introdusa in matematica si teoria sistemelor de catre L. Zadeh in anii '60. Multimile fuzzy si, in general, conceptele fuzzy au aparut ca o necesitate de a masura cantitativ vagul, imprecizia. In comparatie cu multimea conventionala la care apartenenta sau neapartenenta unui element la ea se exclud reciproc, in cazul multimilor fuzzy un element poate avea o apartenenta partiala exprimata prin gradul sau de apartenenta. In consecinta, un anumit element poate sa se gaseasca in trei ipostaze in raport cu o multime fuzzy:

- sa nu apartina multimii, caz in care gradul sau de apartenenta este 0;

- sa apartina multimii in totalitate, caz in care gradul sau de apartenenta este1;
- sa apartina multimii partial, caz in care gradul sau de apartenenta este mai mare ca 0, dar mai mic decat 1.

In cazul multimilor fuzzy se poate lucra cu termeni imprecisi, exprimati prin calificative ca: putin, moderat, mult, foarte bine, greu, usor, etc.ceea ce fac posibile asa numitele rationamente nuantate.

    Retelele Petri au anumite trasaturi care le deosebesc de celelalte tipuri de modele ale sistemelor, si anume:

- relatii explicite intre evenimente;

- existenta unui anumit limbaj ce poate descrie sistemul la diferite nivele de abstractizare;

-reprezentarea retelei permite examinarea proprietatilor sistemului si verificarea corectitudinii procesului.

Retelele Petri stochastice pot fi studiate prin acelasi formalism matematic ca si procesele Markov. Diferenta esentiala consta in faptul ca, spre deosebire de procesele Markov, in cazul retelelor Petri o tranzitie care a devenit executabila va fi in mod cert executata dupa un interval de timp egal cu intarzierea ei.

Utilizarea in fiabilitate a retelelor Petri stochastice este din ce in ce mai extinsa. Tinand cont ca un proces de defectare poate fi considerat ca un proces discret de trecere de la starea de buna functionare la starea de defectare, modelarea cu retele Petri a proceselor complexe de defectare a sistemelor, ca urmare a defectarii componentelor sale este utilizata in multe cazuri datorita faptului ca acestea sunt extrem de versatile si, in acelasi timp, intuitive. Astfel retelele Petri pot inlocui treptat schemele logice de depanare a dispozitivelor electronice prin inglobarea in cadrul unei retele Petri stohastice a principiilor de depanare probabilistic, binar sau pas cu pas. Marcajele nodurilor pot reprezenta probabilitatea de defectare a etajului respectiv sau a componentei iar tranzitiile pot reprezenta prezenta respectiv absenta semnalelor in parametri normali.

Printr-o extensie a retelelor Petri poate fi modelata problema transportului de la o sursa la o destinatie, trecand si prin centre intermediare, exprimata pana acum prin modele de programare liniara si prin grafuri de tip retea de transport. In acest graf a carui alcatuire presupune doua tipuri de noduri, pozitiile vor modela centre, localitati, porturi etc., iar tranzitiile - actiunea de transport intre doua centre.

In extensia propusa se defineste un flux ce tranziteaza reteaua intre pozitia P₀, de intrare si pozitia P_n, de iesire din retea. Executia tranzitiilor defineste drumurile din retea, iar capacitatea minima a tranzitiilor participante la drum determina capacitatea de transport a drumului. Relatia multimilor pozitiilor si tranzitiilor este exprimata cu ajutorul matricei de incidenta.