ALTE DOCUMENTE
|
||||||||||
Calcul vectorial
Marime scalara
Definitie: O marime reprezentata printr-un numar dupa ce s-a fixat o unitate de masura se numeste marime scalara.
Exemple: o densitate, un volum, un unghi, o temperatura, o arie etc.
Marimi vectoriale
Axa
Definitie: Se numeste axa o dreapta (infinita) pe care s-a ales un sens pozitiv. Consideram xx' o astfel de dreapta si sensul pozitiv ales de la x spre x'. Fixam pe aceasta dreapta un segment AB cu lungimea reprezentata prin numarul a(fig.1.1). Lungimea algebrica a segmentului AB este +a, iar a segmentului BA este -a.
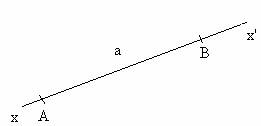
Fig.1.1. Axa
Sens de rotatie
Consideram o axa xx' si un observator situat pe axa în sensul pozitiv. Vom spune ca rotatia este pozitiva sau directa, daca observatorul constata ca se efectueaza de la dreapta spre stânga(fig.1.2)
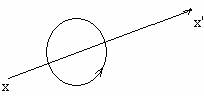
Fig.1.2. Sens de rotatie
În caz contrar, rotatia este negativa sau retrograda.
Triedre directe si inverse
Consideram un triedru oarecare (ortogonal sau nu)(fig.1.3).
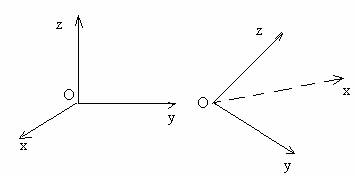
a) Triedru orientat pozitiv b) Triedru orientat negativ
Fig. 1.3. Triedre
Sensul pozitiv ales pe axe este de la O catre x, de la O catre y si de la O catre z. Daca sensul rotatiei în jurul axei Oz, inferioara lui π, care suprapune semiplanul xOz peste semiplanul yOz este pozitiv în raport cu axa Oz, atunci vom spune ca orientarea triedrului este pozitiva, în caz contrar aceasta este negativa (fig.3)
Ordinea în care se considera literele x, y si z este foarte importanta. Astfel, daca triedrele Oxyz, Oyzx, O zxy au aceeasi orientare, atunci triedrele Oxzy, Oyxz, Ozyx au orientare opusa. O singura permutare a literelor x, y, z schimba orientarea, însa doua permutari 353d31d lasa orientarea neschimbata.
Vectori
O marime vectoriala este caracterizata prin doua elemente: un element de natura algebrica, care
reprezinta un numar ce masoara o lungime si un element de natura geometrica, care indica o directie.
1.4.1. Vector legat.
Un vector legat ![]() este
un vector pentru care cunoastem: suportul(xx'), sensul pe suport (de la
este
un vector pentru care cunoastem: suportul(xx'), sensul pe suport (de la
x spre x'), originea(A) si un numar pozitiv care indica lungimea a a segmentului AB(fig.1.4). Acest numar se numeste modulul vectorului.

Fig.1.4. Vector legat
1.4.2. Vector alunecator
Vom spune ca un vector este vector alunecator daca originea lui nu este precizata.
În statica, fortele sunt considerate vectori alunecatori deoarece echilibrul unui corp solid nu se
schimba daca fortele aluneca în lungul suportului lor.
1.4.3. Vector liber
Vom spune ca un vector este liber daca este definit numai prin directia suportului sau si prin
modulul sau. Doi vectori liberi echipolenti sunt identici(fig.1.5)
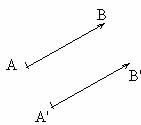
Fig.1.5. Vectori echipolenti
Notatia
folosita pentru vectorii liberi este cu sageata deasupra, ![]()
1.4.4. Vectorul unitar
Vectorul unitar este vectorul al carui modul este egal cu unitatea.
În cazul particular al axelor de coordonate, vectorii unitari ai axelor Ox, Oy, Oz sunt notati prin
![]() .
.
1.4.5. Vectori polari
Anumiti vectori sunt independenti de o schimbare a sensului ales ca sens pozitiv pe axele de
coordonate. De exemplu, o forta, o viteza, un vector câmp electric. În acest caz, spunem ca avem vectori polari.
1.4.6 Vectori axiali
Anumiti vectori îsi schimba semnul atunci când se schimba sensul ales ca sens pozitiv pe una
din axele de coordonate. De exemplu, în cazul produsului vectorial si al vectorului câmp magnetic. Acesti vectori se numesc vectori axiali.
Observatie: Egalitate vectoriala exista doar între vectori axiali si vectori polari.
1.4.7. Unghiul dintre doi vectori
Unghiul dintre
doi vectori ![]() si
si
![]() este unghiul mai mic decat π cu care
trebuie sa rotim un
este unghiul mai mic decat π cu care
trebuie sa rotim un
vector echipolent cu vectorul ![]() ,
dus printr-un punct oarecare, pentru a-l aduce peste un vector echipolent cu
vectorul
,
dus printr-un punct oarecare, pentru a-l aduce peste un vector echipolent cu
vectorul ![]() ,
dus prin acelasi punct. Acest unghi se noteaza cu (
,
dus prin acelasi punct. Acest unghi se noteaza cu (![]() ,
,![]() )
)
Operatii cu vectori
Produsul unui vector cu un scalar
Produsul unui
vector ![]() cu
un scalar c este un vector cu modulul egal cu |c.a|, cu suportul paralel
cu
un scalar c este un vector cu modulul egal cu |c.a|, cu suportul paralel
cu cel al vectorului ![]() ,
de acelasi sens cu vectorul
,
de acelasi sens cu vectorul ![]() ,
daca c este pozitiv si de sens contrar daca c este negativ.
,
daca c este pozitiv si de sens contrar daca c este negativ.
Componentele unui vector
Consideram
trei axe de coordonate ortogonale si proiectiile unui vector ![]() pe aceste axe.
pe aceste axe.
Aceste proiectii sunt trei
vectori: ![]() ,
,
![]() ,
,
![]() .
Putem astfel scrie
.
Putem astfel scrie
![]() (1.1)
(1.1)
Consideram
vectorul unitar ![]() al axei Ox si putem scrie
al axei Ox si putem scrie ![]() (
ax este numarul
(
ax este numarul
care masoara lungimea
algebrica a vectorului ![]() ;
acest numar este pozitiv daca
;
acest numar este pozitiv daca ![]() si
si ![]() au acelasi sens si negativ, în caz
contrar.
au acelasi sens si negativ, în caz
contrar.
Similar putem scrie:
![]() ;
;![]() . (1.2)
. (1.2)
Rezulta:
![]() (1.3)
(1.3)
Numerele algebrice ax, ay, az sunt componentele vectorului pe axele de coordonate.
Adunarea vectorilor
Suma mai multor
vectori ![]() se defineste în modul urmator:
se defineste în modul urmator:
Dintr-un punct
O, ales arbitrar, se duce vectorul ![]() echipolent cu vectorul
echipolent cu vectorul ![]() ;
din
;
din
extremitatea A se duce vectorul ![]() echipolent cu vectorul
echipolent cu vectorul ![]() si
aa mai departe pâna în punctul P, extremitatea vectorului
si
aa mai departe pâna în punctul P, extremitatea vectorului ![]() (fig.1.6)
(fig.1.6)

Fig.1.6. Adunarea vectorilor
Vectorul
![]() este suma vectorilor
este suma vectorilor ![]() .
Aceasta suma este independenta de punctul O. Vectorul suma
este un vector liber pe care îl vom nota cu
.
Aceasta suma este independenta de punctul O. Vectorul suma
este un vector liber pe care îl vom nota cu ![]() .
Adunarea vectoriala se noteaza astfel:
.
Adunarea vectoriala se noteaza astfel:
![]() (1.4)
(1.4)
Adunarea vectoriala este:
comutativa
![]() (1.5)
(1.5)
asociativa
![]() (1.6)
(1.6)
Componenta
pe axa Ox a vectorului ![]() ,
suma vectoriala este egala cu suma componentelor acestor vectori, pe
aceeasi axa.
,
suma vectoriala este egala cu suma componentelor acestor vectori, pe
aceeasi axa.
![]() (1.7)
(1.7)
Produsul scalar
Produsul
scalar(interior) a doi vectori ![]() si
si
![]() este
un scalar obtinut din produsul a trei numere
este
un scalar obtinut din produsul a trei numere
a, b si ![]() ,
în care
,
în care ![]() este
unghiul pe care-l fac între ei cei doi vectori
este
unghiul pe care-l fac între ei cei doi vectori ![]() si
si
![]() .
.
Produsul scalar este:
- comutativ ![]()
- distributiv ![]()
Observatii:
Daca produsul scalar a doi vectori nenuli este
nul, atunci cei doi vectori sunt ortogonali; ![]() si
si ![]() .
.
Produsul scalar al unui vector prin el însusi este
egal cu patratul modulului acelui vector ![]() .
.
Daca ![]() ,
,
![]() ,
,
![]() sunt vectorii unitari ai axelor de coordonate,
atunci se poate scrie:
sunt vectorii unitari ai axelor de coordonate,
atunci se poate scrie:
![]() (1.8)
(1.8)
![]() (1.9)
(1.9)
Produsul scalar în coordonate carteziene
Consideram
proiectiile a doi vectori ![]() si
si
![]() pe
axele de coordonate Ox, Oy si Oz: ax, bx, ay,
by,
pe
axele de coordonate Ox, Oy si Oz: ax, bx, ay,
by,
az, bz.
Produsul scalar cu aceste componente are expresia:
![]() (1.10)
(1.10)
Efectuam produsele din relatia de mai sus si obtinem:
![]() (1.11)
(1.11)
Formula de mai sus, împreuna cu definitia produsului scalar, conduce la expresia cosinusului
unghilului dintre cei doi vectori
![]() si
si
![]() în
functie de componentele acestor vectori:
în
functie de componentele acestor vectori:
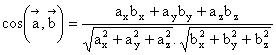 (1.12)
(1.12)
Produsul vectorial
Produsul
vectorial(exterior) a doi vectori ![]() si
si
![]() este
un vector
este
un vector ![]() perpendicular pe cei doi
perpendicular pe cei doi
vectori ![]() si
si
![]() ,
al carui modul este egal cu produsul
,
al carui modul este egal cu produsul ![]() si care are fata de cei doi
vectori o orientare pozitiva. Produsul vectorial a doi vectori se noteaza
si care are fata de cei doi
vectori o orientare pozitiva. Produsul vectorial a doi vectori se noteaza
![]() .
.
Observatie: Daca niciunul din
cei doi vectori ![]() si
si
![]() nu
este nul, si daca
nu
este nul, si daca ![]() ,
atunci
,
atunci
suportii vectorilor sunt
paraleli, deoarece ![]() .
.
Modulul
vectorului ![]() este egal cu numarul care
masoara aria paralelogramului construit pe
este egal cu numarul care
masoara aria paralelogramului construit pe
vectorii echipolenti cu ![]() si
si
![]() ,
dusi printr-un punct O din spasiu(fig.1.7).
,
dusi printr-un punct O din spasiu(fig.1.7).

Fig.1.7: Produsul vectorial a doi vectori
Suportul produsului vectorial este perpendicular pe planul OAB. Sensul sau este astfel încât o
rotatie mai mica decât
π , care aduce vectorul ![]() peste vectorul
peste vectorul ![]() sa fie în sensul pozitiv.
sa fie în sensul pozitiv.
Produsul vectorial în coordonate carteziene
Produsul vectorial în coordinate carteziene are expresia:
![]() (1.13)
(1.13)
Sub forma de determinant produsul vectorial are expresia:
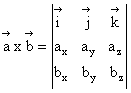 (1.14)
(1.14)
Proprietatile produsului vectorial
Produsul vectorial nu este comutativ
Produsul vectorial nu este asociativ
Produsul vectorial este distributiv ![]()
Distributivitatea se poate scrie si sub forma de determinanti, astfel
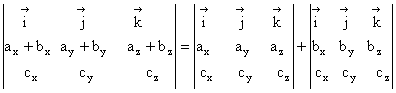 (1.15)
(1.15)
Produsele vectoriale ale vectorilor unitari sunt date de relatiile:
![]() ;
; ![]() ;
; ![]() (1.16)
(1.16)
Produsul mixt a trei vectori
Produsul mixt a trei vectori este dat de relatia:
![]() (1.17)
(1.17)
În relatia de mai sus aplicam formulele cunoscute de la produsul scalar si produsul vectorial si
obtinem:
![]() (1.18)
(1.18)
În scrierea cu determinanti produsul mixt are forma:
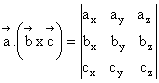 (1.19)
(1.19)
Se constata ca produsul mixt a trei vectori este egal cu numarul care masoara volumul
paralelipipedului construit pe cei trei vectori ![]() ,
,
![]() ,
,
![]() echipolenti cu vectorii
echipolenti cu vectorii ![]() ,
,
![]() ,
,
![]() dusi printr-un punct O. Volumul este
pozitiv sau negativ dupa cum orientarea celor trei vectori este pozitiva
sau negativa.
dusi printr-un punct O. Volumul este
pozitiv sau negativ dupa cum orientarea celor trei vectori este pozitiva
sau negativa.
Identitati:
![]()
![]()
Relatia 1 de mai sus indica faptul ca vectorii se pot permuta circular. Relatia 2 ne arata ca se pot
schimba semnele înmultirii scalare si înmultirii vectoriale.
Produsul mixt se noteaza
prescurtat cu ![]() sau
sau ![]() .
.
Dublul produs vectorial a trei vectori
Expresia pentru calculul dublului produs vectorial a trei vectori este:
![]() (1.20)
(1.20)
Operatii diferentiale asupra vectorilor
6.1. Derivata unui vector
Consideram
ca fiecarei valori a unei variabile t îi facem sa-i corespunda
un vector ![]() :
:![]() .
Efectuam o crestere a variabilei t cu Δt. Construim un nou
vector
.
Efectuam o crestere a variabilei t cu Δt. Construim un nou
vector![]() (t+
Δt). Vectorul Δ
(t+
Δt). Vectorul Δ![]() =
=![]() (t+
Δt) -
(t+
Δt) -![]() (t).
Daca modulul vectorului Δ
(t).
Daca modulul vectorului Δ![]() tinde catre zero, atunci când Δt tinde catre zero, atunci vom
spune ca vectorul
tinde catre zero, atunci când Δt tinde catre zero, atunci vom
spune ca vectorul ![]() (t)
este o functie continua. Limita vectorului
(t)
este o functie continua. Limita vectorului ![]() se numeste derivata vectorului
se numeste derivata vectorului ![]() (t)
în raport cu t. Notatiile uzuale pentru derivata sunt:
(t)
în raport cu t. Notatiile uzuale pentru derivata sunt: ![]() sau a'(t) sau
sau a'(t) sau
![]()
Similar, se pot defini si derivatele de ordin superior pentru un vector.
Daca vectorul ![]() depinde de mai multe variabile, atunci putem
defini derivatele partiale de diverse ordine.
depinde de mai multe variabile, atunci putem
defini derivatele partiale de diverse ordine.
1.6.2. Derivata unui vector în raport cu alt vector
Consideram
doi vectori ![]() si
si
![]() .
Definim derivata vectorului
.
Definim derivata vectorului ![]() în
raport cu vectorul
în
raport cu vectorul ![]() prin
vectorul dat de expresia:
prin
vectorul dat de expresia:
 (1.21)
(1.21)
care se noteaza prin ![]() .
.
Proiectiile acestui vector pe axele de coordonate sunt:
![]()
![]() (1.22)
(1.22)
![]()
1.6.3. Formule de derivare a vectorilor
1.6.3.1. Derivata unei sume de vectori
Derivata unei sume de vectori este egala cu suma derivatelor vectorilor sumei. Astfel, fie urmatoarea suma de vectori:
![]() (1.23)
(1.23)
Derivata acestei sume are expresia:
![]() (1.24)
(1.24)
1.6.3.2. Derivata unui produs dintre un numar si un vector.
Fie vecorul ![]() obtinut din produsul unui vector
obtinut din produsul unui vector ![]() cu un numar n
cu un numar n
![]() (1.25)
(1.25)
Derivata acestui produs este data de expresia:
![]() (1.26)
(1.26)
1.6.3.3. Derivata produsului dintre un vector si un scalar
Consideram un scalar f(t) si un
vector ![]() (t)
ca functii de vatiabila t. Vom studia derivata produsului
(t)
ca functii de vatiabila t. Vom studia derivata produsului
![]() (1.27)
(1.27)
Expresia acestei derivate este:
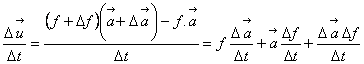 (1.28)
(1.28)
Trecem la limita expresia de mai sus si obtinem:
![]() (1.29)
(1.29)
1.6.3.4. Derivata unui produs scalar
Consideram urmatorul produs
scalar ![]() ,
unde
,
unde ![]() si
si ![]() .
.
Derivata acestui produs scalar este data de expresia:
 (1.30)
(1.30)
Trecem la limita expresia de mai sus si obtinem:
![]() (1.31)
(1.31)
1.6.3.5. Derivata unui produs vectorial
Consideram urmatorul produs vectorial
![]() (1.32)
(1.32)
Derivata acestui produs vectorial de obtine cu ajutorul expresiei:
![]() (1.33)
(1.33)
Observatie:
![]() (1.34)
(1.34)
Teorema:
Derivata modulului unui vector se obtine prin expresia:
 (1.35)
(1.35)
Teorema:
Daca un vector nenul ![]() satisface relatia
satisface relatia ![]() ,
atunci el este paralel cu o directie fixa si
,
atunci el este paralel cu o directie fixa si
![]()
1.6.4. Integrala unui vector
Consideram un vector ![]() ca functie de t. Expresia lui
ca functie de t. Expresia lui ![]() în functie de proiectiile pe axele
de coordonate este:
în functie de proiectiile pe axele
de coordonate este:
![]() (1.36)
(1.36)
Fie t0 si t1 doua valori ale variabilei t. Integrala unui vector are expresia:
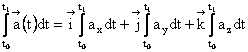 (1.37)
(1.37)
Functii de punct
În inginerie se întâlnesc frecvent marimi care depind de pozitia unui punct si care pot depinde si de o alta variabila, alta decât coordonatele spatiale x, y, z ale punctului; în general, aceasta variabila este timpul t. Daca o astfel de marime este un numar, vom spune ca este vorba de o functie scalara de punct, iar daca este un vector, vom spune ca este o functie vectoriala de punct. În zona spatiala în care o astfel de functie este definita exista un câmp scalar, respectiv un câmp vectorial.
De exemplu, densitatea electrica care exista în diferite puncte ale unui corp izolat electrizat este o functie scalara de punct. Dar, în acelasi timp, câmpul electric creat de aceste sacini în diverse puncte ale corpului este o functie vectoriala de punct. Sarcinile electrice au creat, deci, un câmp scalar de densitate electrica si un câmp vectorial de forte electrice.
Pentru astfel de probleme se definesc trei functii importante:
1.7.1. Gradientul
Consideram o functie scalara f(x, y, z). Gradientul acestei functii scalare este un vector ale carui componente sunt
![]() (1.38)
(1.38)
iar
![]() (1.39)
(1.39)
Consideram
un punct M(x, y, z) si M+ ![]() un punct infinit vecin (fig.1.8). Produsul
scalar grad f.
un punct infinit vecin (fig.1.8). Produsul
scalar grad f.![]() este egal cu df.
este egal cu df.
Într-adevar,
![]() = df (1.40)
= df (1.40)
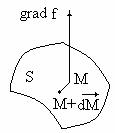
Fig.1.8. Gradientul
Raportul ![]() se numeste derivata functiei scalare în functie
de punctul M, pe directia considerata
se numeste derivata functiei scalare în functie
de punctul M, pe directia considerata ![]() .
.
Expresia (1.40)
ne arata ca aceasta derivata este egala cu
proiectia vectorului grad f pe directia ![]() ,
deoarece
,
deoarece
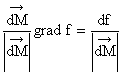 (1.41)
(1.41)
1.7.2. Derivata normala
Daca se considera normala în punctul M la o suprafata oarecare Σ care trece prin acest punct(fig.1.9), atunci derivata functiei f în raport cu punctul M pe directia normalei se numeste derivata normala a functiei f în raport cu suprafata Σ.
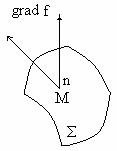
Fig.1.9: Derivata normala
Daca n este vectorul unitar al acestei normale, atunci derivata aceasta este egala cu grad f.n, adica este egala cu proiectia vectorului grad f pe normala.
1.7.3. Suprafete de nivel
Suprafetele de nivel sunt definite de expresia:
f(x, y, z) = const. (1.42)
Ecuatia suprafetei de nivel care trece prin punctul de coordonate (x0, y0, z0) este data de expresia:
f(x, y, z) = f(x0, y0, z0) (1.43)
Aceasta suprafata este unica daca functia f(x, y, z) este uniforma.
Vectorul grad f într-un punct este normal la suprafata de nivel care trece prin acel punct. Derivata normala a lui f în raport cu suprafata de nivel este egala cu grad f.
1.7.4. Semnificatia vectorului grad f
Vectorul gradient descrie foarte bine proprietatile functiei f în jurul punctului M considerat. Variatia functiei f în jurul acestui punct este determinata de cunoasterea acestui vector. În particular, cea mai mare variatie a lui f are loc atunci când deplasarea se face de-a lungul normalei la suprafata de nivel. Aceasta variatie maxima este definita în marime si în directie de vectorul grad f.
Observatie: Vectorul grad f este
independent de alegerea axelor de coordonate, asa cum rezulta din
expresia f. ![]() = df.
= df.
1.7.5. Linii de forta
Prin linie de forta întelegem acea linie la care vectorul grad f este, în mod constant, tangent. Definitia vectoriala a liniilor de forta este data de expresia:
![]() (1.44)
(1.44)
Definitia carteziana este data de expresia:
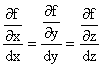 (1.45)
(1.45)
Asadar, liniile de forta sunt traiectoriile ortogonale ale suprafetelor de nivel
f(x, y, z) = const. (1.46)
Tub de forta
Un tub de forta este o suprafata descrisa de o linie de forta care se sprijina pe un contur închis C(fig.1.10).
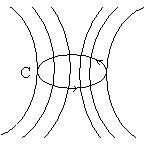
Fig.1.10: Tub de forta
1.7.6. Gradientul unei functii scalare compuse
Consideram un scalar f(m, n, .) ca functie de mai multi scalari care sunt functii de coordonatele x, y, z, atunci grad f are expresia:
![]() (1.47)
(1.47)
si
![]() (1.48)
(1.48)
Însa dm = grad
m.![]() ;
dn = grad n.
;
dn = grad n. ![]() ;
.
;
.
Cum ![]() este oarecare, obtinem formula (1.47)
este oarecare, obtinem formula (1.47)
Observam ca simbolul grad se comporta ca simbolul diferentierii.
1.7.7. Divergenta
Consideram
un vector ![]() ca
functie de punctul M(x, y, z) si ax, ay, az
componentele vectorului
ca
functie de punctul M(x, y, z) si ax, ay, az
componentele vectorului ![]() pe axele de coordonate.
pe axele de coordonate.
Divergenta
vectorului ![]() este marimea scalara data de
expresia:
este marimea scalara data de
expresia:
![]() (1.49)
(1.49)
1.7.8. Rotorul
Rotorul
unui vector ![]() este marimea vectoriala
obtinuta prin expresia:
este marimea vectoriala
obtinuta prin expresia:
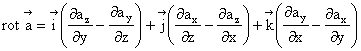 (1.50)
(1.50)
Observam expresiile
componentelor vectorului rot ![]() pe axele de coordonate
pe axele de coordonate
Pe axa Ox
![]() (1.51)
(1.51)
Pe axa Oy
![]() (1.52)
(1.52)
Pe axa Oz
![]() (1.53)
(1.53)
Observatii:
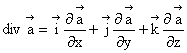 (1.54)
(1.54)
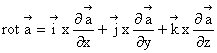 (1.55)
(1.55)
1.7.9. Operatorul Laplacian
Operatorul Laplacian are expresia:
![]() (1.56)
(1.56)
Aplicam operatorul Laplacian unei functii scalare, f si obtinem:
![]() (1.57)
(1.57)
Denumirea
de Laplacian provine de la ecuatia lui
Δf = 0 (1.58)
Aplicam
operatorul Laplacian unui vector ![]() si obtinem:
si obtinem:
 (1.59)
(1.59)
Însa vectorul ![]() se poate scrie în functie de componentele
pe axele de coordonate
se poate scrie în functie de componentele
pe axele de coordonate
![]() (1.60)
(1.60)
si
![]() (1.61)
(1.61)
Rezulta ca ![]() este un vector.
este un vector.
1.7.10. Utilizarea vectorului simbolic "nabla"( )
Operatorul vectorial notat prin are urmatoarea expresie:
![]() (1.62)
(1.62)
Aplicam acest operator vectorial nabla unui scalar f si obtinem:
![]() (1.63)
(1.63)
Produsul
scalar dintre vectorul simbolic si un vector ![]() ,
functie de punct, are expresia:
,
functie de punct, are expresia:
![]() (1.64)
(1.64)
Produsul
vectorial dintre vectorul simbolic si un vector ![]() ,
functie de punct, are expresia:
,
functie de punct, are expresia:
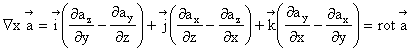 (1.65)
(1.65)
Observam ca ![]() si
si ![]() unde
unde ![]() este
un operator scalar.
este
un operator scalar.
Derivata unui vector ![]() în raport cu vectorul
în raport cu vectorul ![]() se poate scrie astfel
se poate scrie astfel
![]() (1.66)
(1.66)
sau
![]() (1.67)
(1.67)
Se constata ca
![]() (1.68)
(1.68)
ceea ce înseamna
rot
rot ![]() = grad div
= grad div ![]() -
Δ
-
Δ![]() (1.69)
(1.69)
1.8. Problema
Fie
f:R3 → R, ![]() (1.70)
(1.70)
în care ![]() , si
, si ![]() ,
, ![]() sunt vectori
constanti.
sunt vectori
constanti.
Se cere sa se calculeze grad f
Solutie:
![]()
![]()
![]() (1.71)
(1.71)
![]()
Problema
Se cere sa se calculeze ![]() unde f este dat in
problema precedenta, iar
unde f este dat in
problema precedenta, iar![]() este o directie data
este o directie data
Solutie:
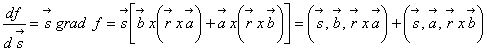 (1.72)
(1.72)
1.10.Câmpul vectorial. Linii vectoriale
1.10.1. Câmp vectorial
Consideram în spatiu un domeniu D(fig.1.11).
Fiecarui punct M îi vom atribui un vector ![]() cu o valoare numerica si o orientare bine determinate. Vom
numi pe
cu o valoare numerica si o orientare bine determinate. Vom
numi pe ![]() functie vectoriala de punct în
domeniul considerat, adica
functie vectoriala de punct în
domeniul considerat, adica
![]() =
= ![]() (M) (1.73)
(M) (1.73)
Domeniul D este câmpul vectorial al vectorului ![]() . Pentru a definin un câmp vectorial trebuie sa
indicam legea conform careia putem determina în orice punct M al
domeniului considerat atât marimea cât si orientarea vectorului.
. Pentru a definin un câmp vectorial trebuie sa
indicam legea conform careia putem determina în orice punct M al
domeniului considerat atât marimea cât si orientarea vectorului.
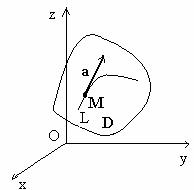
Fig.1.11: Câmp vectorial
În coordonate carteziene rectangulare, unde
![]() (1.74)
(1.74)
trebuie sa cunoastem cele trei proiectii ale vectorului
ax = ax(x, y, z); ay = ay(x, y, z); az = az(x, y, z) (1.75)
sub forma a trei functii scalare de coordonatele x, y, z. ale punctului M.
Exista, în fizica, multe câmpuri vectoriale, de exemplu: câmpul electrostatic al unor sarcini punctiforme, câmpul magnetic al unui conductor parcurs de curent, câmpul gradientului unei functii scalare oarecare f.
În mecanica exista câmpuri vectoriale ale vitezelor si acceleratiilor unui solid într-un moment oarecare, fiecarui punct al solidului în miscare fiindu-i atribuite un vector viteza si un vector acceleratie.
În cele ce urmeaza ne vom ocupa de câmpuri vectoriale în general. În particular, când vectorul reprezinta o forta vom spune ca avem un câmp de forte.
Exista multe metode de creare a câmpurilor vectoriale întâlnite în teoria electricitatii, a magnetismului, a elasticitatii, mecanica fluidelor, teoria potentialului etc.
1.10.2. Linii vectoriale
Prima metoda de studiu a câmpurilor vectoriale consta din trasarea asa numitelor linii vectoriale. Vectorul câmp este tangent la linia vectoriala în fiecare punct al ei(fig.7) În cazul particular al câmpurilor de forte, liniile vectoriale sunt numite linii de forta, în mecanica fluidelor se numesc linii de curent etc.
Linia de forta a unui câmp electrostatic reprezinta linia de-a lungul careia s-ar misca o sarcina libera +1, fara viteza initiala, ea fiind doar sub actiunea fortelor câmpului.
Determinam ecuatia diferentiala a liniei vectoriale.
Observam în figura 3.2
vectorul de pozitie ![]() al punctului curent M, care apartine acestei linii
si satisface relatia
al punctului curent M, care apartine acestei linii
si satisface relatia
![]() =
=![]() (s) (1.76)
(s) (1.76)
care reprezinta ecuatia sub forma vectoriala.
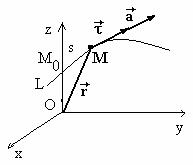
Fig.1.12: Linii vectoriale
Punem
conditia ca vectorul câmp ![]() sa coincida
în fiecare punct M cu versorul tangent
sa coincida
în fiecare punct M cu versorul tangent 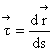 . Este suficient sa punem conditia ca
. Este suficient sa punem conditia ca ![]() si
si ![]() sa fie paraleli, deoarece au un punct comun M,
obtinem:
sa fie paraleli, deoarece au un punct comun M,
obtinem:
 (1.77)
(1.77)
Relatia de mai sus este chiar ecuatia cautata. Pentru a o transpune în forma analitica folosim faptul ca proiectiile vectorilor paraleli sunt proportionale între ele.
Obtinem:
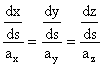 (1.78)
(1.78)
sau
![]() (1.79)
(1.79)
Am obtinut un sistem de ecuatii diferentiale scrise sub forma de proportii. Prin urmare, problema determinarii liniilor vectoriale se reduce la integrarea unui sistem de ecuatii diferentiale de forma de mai sus.
Presupunem ca am gasit doua integrale independente ale sistemului de mai sus
f1(x, y, z) = C1
f2(x, y, z) = C2 (1.80)
Ansamblul celor doua ecuatii va determina linia vectoriala, aceasta constituind intersectia a doua suprafete. Modificând arbitrar parametrii C1 si C2, vom obtine o familie de linii vectoriale care depind de doi parametri. În cazul general, integrarea sistemului de ecuatii diferentiale de mai sus este uneori foarte dificila. De aceea, în practica, se obisnuieste mai ales în cazul câmpurilor plane si paralele, sa se traseze liniile prin metode grafice aproximative.
1.10.3. Densitatea liniilor vectoriale
Deoarece putem lua
drept punct initial orice punct A, pentru trasarea liniei vectoriale,
înseamna ca numarul liniilor este infinit si din punct de
vedere teoretic, ele pot acoperi întregul domeniu D în mod uniform. Câmpul
vectorial are o densitate diferita a liniilor vectoriale în diferitele
sale puncte; densitatea este mai mare acolo unde a este mai mare si invers. Daca vectorul ![]() are aceeasi
marime, orientare si sens în toate punctele unui domeniu oarecare, atunci
liniile vectoriale vor umple câmpul în mod uniform. Acest câmp se va numi câmp uniform.
are aceeasi
marime, orientare si sens în toate punctele unui domeniu oarecare, atunci
liniile vectoriale vor umple câmpul în mod uniform. Acest câmp se va numi câmp uniform.
Problema:
Intensitatea H a campului lung si rectiliniu în punctele exterioare se determina prin expresiile:
![]()
unde
![]()
Se cere sa se determine liniile vectoriale si forma lor.
Solutie:
Scriem sistemul de ecuatii diferentiale corespunzator problemei noastre
![]()
Deducem ca dz = 0 deoarece numai în acest caz ulimul raport poate fi egal cu primele doua.
Rezulta:
z = const. = C1
Ecuatia de
mai sus reprezinta o familie de plane paralele cu planul xOy, situate la
distante corespunzatoare diferitelor valori pe care le ia
Din primele doua relatii obtinem:
x.dx + y. dy = 0
sau
![]()
de unde rezulta:
![]()
Am obtinut o familie de cilindri circulari drepti. Axele lor coincid cu axa z, iar razele sunt determinate de C2.
Ansamblul ecuatiilor
z = const. = C1
![]()
determina liniile vectoriale ca fiind intersectia de plane cu familia de suprafete cilindrice. Liniile reprezinta niste cercuri cu centrele situate pe axa z. Cercurile se afla în plane perpendiculare pe axa conductorului.
Daca am fi studiat proiectiile câmpului magnetic interior
Hx = -2π u y; Hy = 2πux; Hz = 0
am fi obtinut un sistem de ecuatii diferentiale de forma de mai sus. Prin urmare si liniile vectoriale ale câmpului interior reprezinta niste cercuri.
1.11. Formule utile
Gradientul produsului scalar
 (1.81)
(1.81)
Demonstratie:
 (1.82)
(1.82)
![]()
 (1.83)
(1.83)
Dezvoltam expresiile din relatia de mai sus
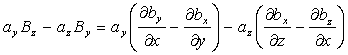 (1.84)
(1.84)
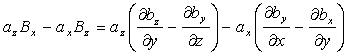 (1.85)
(1.85)
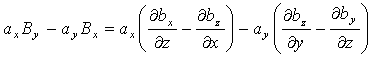 (1.86)
(1.86)
Relatii
similare gasim pentru expresia ![]() înlocuind pe a cu b
si pe b cu a.
înlocuind pe a cu b
si pe b cu a.
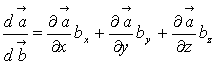 (1.87)
(1.87)
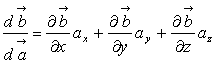 (1.88)
(1.88)
Proiectiile vectorului ![]() pe axele de coordonate
sunt:
pe axele de coordonate
sunt:
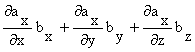 (1.89)
(1.89)
 (1.90)
(1.90)
 (1.91)
(1.91)
Similar obtinem proiectiile vectorului ![]() pe axele de coordonate
înlocuind în expresiile de mai sus pe a cu b si pe b cu a.
pe axele de coordonate
înlocuind în expresiile de mai sus pe a cu b si pe b cu a.
Produsul scalar are expresia:
![]() (1.92)
(1.92)
Proiectia pe axa Ox a gradientului din expresia noastra este:
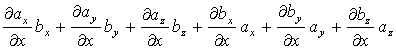 (1.93)
(1.93)
Proiectia membrului drept al relatiei date pe axa Ox este:
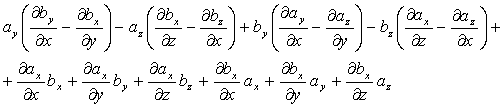 (1.94)
(1.94)
Efectuând reducerile de termeni, relatia din enunt este evidenta pentru proiectia pe axa Ox. Similar se demonstreaza si pentru proiectiile pe celelalte axe de coordonate.
Divergenta produsului dintre o functie scalara si o functie vectoriala
Expresia divergentei produsului dintre o functie scalara si o functie vectoriala este:
![]() (1.95)
(1.95)
În forma dezvoltata expresia de mai sus este:
![]() (1.96)
(1.96)
sau
 (1.97)
(1.97)
Divergenta unui produs vectorial
![]() (1.98)
(1.98)
Se stie ca:
![]() (1.99)
(1.99)
si, deci, se vor folosi relatiile:
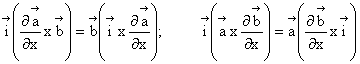 (1.100)
(1.100)
Divergenta unui gradient
![]() (1.101)
(1.101)
Demonstratie:
Se aplica formulele cunoscute de la definitile gradientului si divergentei
![]() (1.102)
(1.102)
Divergenta unui rotor
![]() (1.103)
(1.103)
Demonstratie:
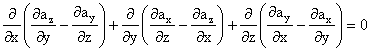 (1.104)
(1.104)
Divergenta unui Laplacian
![]() (1.105)
(1.105)
Demonstratia se bazeaza pe expresia:
![]() (1.106)
(1.106)
1.11.7. Rotorul unui gradient
![]() (1.107)
(1.107)
Demonstratie:
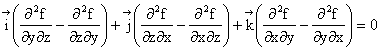 (1.108)
(1.108)
1.11.8. Rotorul produsului dintre o functie scalara si o functie vectoriala
![]() (1.109)
(1.109)
1.11.9. Rotorul produsului vectorial
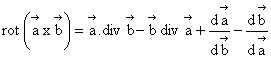 (1.110)
(1.110)
1.11.10. Rotor din rotor
![]() (1.111)
(1.111)
Demonstratie:
Notam:
 (1.112)
(1.112)
Avem
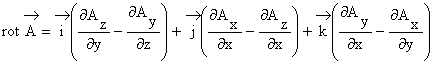 (1.113)
(1.113)
Dezvoltam proiectia pe axa Ox
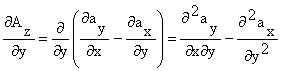 (1.114)
(1.114)
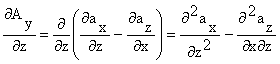 (1.115)
(1.115)
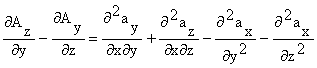 (1.116)
(1.116)
În expresia de mai sus adunam si scadem termenul ![]() si obtinem:
si obtinem:
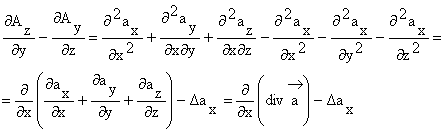 (1.117)
(1.117)
Similar, efectuam prelucrarile pentru proiectiile pe axele Oy si Oz si astfel formula este demonstrata.
|