ALTE DOCUMENTE |
MCIMLucrarea 17 |
Calculele numerice cu polinoame |
Functiile MATLAB pentru calcule cu polinoame sunt:
conv calculeaza produsul a doua polinoame;
deconv calculeaza câtul si restul împartirii a doua polinoame;
poly calculeaza coeficientii unui polinom cu radacinile date;
polyval evalueaza un polinom la valorile precizate ale variabilei;
polyder calculeaza derivata polinoamelor;
polyflit aproximeaza un set de date cu polinomul de grad n; 242y241c
residue descompune în fractii simple raportul a doua polinoame;
roots calculeaza radacinile unui polinom.
1.Evaluarea polinoamelor
În MATLAB exista mai multe metode pentru evaluarea polinoamelor. Vor fi exemplificate, cu polinomul:
f(x)=3x4-x3+x-1
Cea mai simpla metoda este evaluarea cu scalari, adica pentru o singura valoare a variabilei. Se efectueaza operatiile cu scalari, ca în exemplul:
x=1;
f=3*x^4-x^3+x-1
obtinându-se rezultatul:
f=2
A doua metoda consta în evaluarea polinomului în mai multe puncte. Evaluarea polinomului f(x) în punctele -2, 0, 1, 2.5, 3,se face cu secventa MATLAB:
x=[-2 0 1 2.5 3];
f=3*x.^4-x.^3+x-1
obtinându-se rezultatul:
f=[53.0000 -1.0000 2.0000 103.0625 218.0000]
A treia metoda de evaluare a polinoamelor consta în utilizarea functiei polyval; se apeleaza cu sintaxa:
f= polyval(p,s)
Pentru evaluarea polinomului luat ca exemplul, în punctele -2, 0, 1, 2.5, 3, secventa MATLAB este urmatoarea:
p=[3 -1 0 1 -1];
x=[-2 0 1 2.5 3];
f=poyval (p,x)
iar rezultatul obtinut este:
f=[53.0000 -1.0000 2.0000 103.0625 218.0000]
Pentru evaluarea unui polinom pe un interval, se genereaza în primul rând un vector al punctelor de evaluare, cu sau fara pas constant, si apoi se procedeaza ca mai sus. Evaluarea polinomului f(x), definit anterior, în 300 puncte pe intervalul [0,5], se poate face cu secventa MATLAB:
x=0:5/300:5;
p=[3 -1 0 1 -1];
f=polyval(p,x)
2.Adunarea si scaderea
Fie doua polinoame g(x) si h(x) ai caror coeficienti sunt înregistrati în vectorii linie g si h. Operatiile aritmetice de adunare si scadere a polinoamelor presupun adunarea si scaderea coeficientilor de acelasi ordin. Spre exemplul, pentru:
g(x)=x4-3x2-x+2
h(x)=2x2+5x-16
s(x)=g(x)+h(x)
u(x)=g(x)-h(x)
dimensiunea vectorului coeficientilor va fi 5, iar polinoamele echivalente pentru care se scriu vectorii coeficientilor sunt:
g(x)=x4+0x3-3x2-x+2
h(x)=0x4+0x3+2x2+5x-16
Secventa MATLAB care realizeaza operatiile de mai sus este:
g=[1,0,-3,-1,2];
h=[0, 0,2,5,-16];
s=g+h
u=g-h
obtinându-se rezultatele: s=[1 0 -1 4 -14]
u=[1 0 -5 -6 18]
respectiv polinoamele: s(x)=x4-x2+4x-14
u(x)=x4-5x2-6x+18
3.Înmultirea si împartirea
Înmultirea a doua polinoame este echivalenta unei operatii de convolutie; este realizata cu functia MATLAB conv, care se apeleaza cu sintaxa:
c=conv(a,b)
unde: a si b sunt vectorii coeficientilor polinoamelor care se înmultesc;
c este vectorul coeficientilor polinomului produs c(x)=a(x)b(x).
Împartirea a doua polinoame este echivalenta unei operatii de deconvolutie; este realizata cu functia MATLAB deconv, care se apeleaza cu sintaxa: [d,r]=deconv(a,b)
unde: a si b sunt vectorii coeficientilor polinoamelor deîmpartit si împartitor;
d este vectorul coeficientilor polinomului cât;
r este vectorul coeficientilor polinomului rest, rezultat al operatiei: a(x)=d(x)b(x)+r(x)
Pentru ilustrarea modului de
utilizare a functiilor conv si
deconv la înmultirea si împartirea polinoamelor, fie
calculele: g(x)=(x2+x-2)(x+1) h(x)= ![]()
Cu notatiile: g(x)=g1(x)g2(x) h(x)= ![]()
si secventa MATLAB: g1=[1 1 -2]; g2=[1 1];
f=[1 2 0 -2]; e=[1 0 1];
g=conv (g1,g2)
[h,r]=deconv (f,e)
se obtin rezultatele: g=[1 2 -1 -2]
h=[1 2]
r=[0 0 -1 -4]
care reprezinta polinomul produs: g(x)=x3+2x2-x-2
polinomul cât: g(x)=x+2
si restul: r(x)=-x -4
4.Descompunerea în fractii simple
Prin descompunerea în fractii simple se întelege scrierea raportului a doua polinoame ca suma de fractii cu polinoame de ordinul unu.
Functia MATLAB residue se apeleaza cu sintaxa: [r,p,k]=residue (B,A)
unde: A, B - vectorii linie ai coeficientilor polinoamelor numitor si numarator, în ordinea descrescatoare a puterilor variabilei;
r-vectorul coloana al rezidurilor;
p-vectorul coloana al polilor;
k-vectorul linie al termenilor liberi.
Daca functia residue se apeleaza cu sintaxa: [B,A]=residue (r,p,k) se returneaza coeficientilor polinoamelor B si A, numaratorul si numitor, al caror raport are rezidurile r, polii p si termenii liberi k.
Exemplul 4.1. Sa se descompuna în functii simple expresia:
![]() =
= 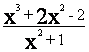 Cu secventa
MATLAB:
Cu secventa
MATLAB:
B=[1 2 0 -2];
A=[1 0 1];
[r, p,k]=residue (B,A)
se obtin rezultatele:
r= p= k=
-0.5000+2.0000i 0+1.0000i 1 2
-0.50000-2.0000i 0-1.0000i
care reprezinta urmatoarea descompunere în fractii simple:
![]() =
=![]()
5.Calculul derivatei
Derivata unui polinom în MATLAB utilizeaza functia polyder, care se apeleaza cu sintaxa:
D=polyder(C)
unde C este vectorul linie al coeficientilor polinomului, în ordinea descrescatoare a puterilor variabilei, iar D este vectorul linie al coeficientilor polinomului derivat. Apelata cu sintaxa: D=polyder(A,B)
functia polyder returneaza în vectorul D coeficientii derivatei polinomului produs AB:
D(x)=(A(x) B(x))=A'(x) B(x)+A(x) B'(x)
Apelata cu sintaxa: [M,N]=polyder(A,B) functia polyder returneaza în vectorii M si N coeficientii numaratorului si numitorului derivatei raportului polinoamelor A/B:
![]()
![]()
![]()
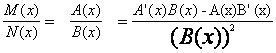
Exemplul.5.1.Fie polinoamele: A(x)=x2+2x-1 B(x)=x-1 Calculati derivatele polinoamelor:
Cu secventa MATLAB:
A=[1 2 -1]; B=[1 -1];
Ad=polyder(A)
Bd=polyder(B)
Cd=polyder(A,B)
[M,N]=polyder(A,B)
se obtin rezultatele:
Ad=[2 2] Bd= 1 Cd=[3 2 -3]
M=[1 -2 -1] N=[1 -2 1]
care reprezinta polinoamele:
Ad(x)=2x+2 Bd(x)=1
Cd(x)=3x2+2x+3 Dd(x)=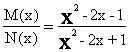
6.Calculul radacinilor
Functia MATLAB roots determina radacinile polinoamelor; se apeleaza cu sintaxa:
r=roots(c)
Functia MATLAB poly determina coeficientii unui polinom ale carui radacini sunt cunoscute; se apeleaza cu sintaxa: c=poly(r). În ambele cazuri:
c-este un vector linie, care contine coeficientii polinomului, în ordine descrescatoare a puterilor variabilei;
r-este un vector coloana care contine radacinile polinomului .
Exemplul 6.1. Determinati radacinile polinomului:
f(x)= x3-2x2-3x+10 si efectuati verificarea rezultatului.
Cu secventa MATLAB:
p=[1,-2,-3,10]; r=roots(p)
se obtine rezultatul: r=
2.0000+1.0000i
2.0000-1.0000i
-2.0000
cu secventa MATLAB:
c=[1,-2,-3,10]; % coeficientii
r=[2+i 2-i -2]; % radacinile
v=polyval(c,r)
se obtine rezultatul:
v=[0 0].
|