Criteriile de stabilitate reprezinta niste metode prin care se da raspuns la teorema fundamentala a stabilitatii fara a apela in mod explicit la criteriul radacinilor, adica fara a rezolva ecuatia caracterisitica. In mod obisnuit incadram un criteriu de stabilitate in functie de domeniul timp (pentru un STC sau STD) si in functie de abordarea in domeniul operational (criterii algebrice si criterii frecventiale).
A. Criteriul lui Hurwitz
Este un criteriu algebric care se aplica STC. Punctul de plecare il reprezinta polinomul caracteristic al sistemului. Enuntul pe care il folosim este valabil in cazul cand polinomul caracteristic are forma monica. (sn are coeficientul 1).
Presupunem un STC cu polinom 222h75c ul caracteristic:
μ(s)= sn + an-1sn-1 + . + a1s + a0 (1)
Cu ajutorul coeficientilor se construieste un determinant de ordinul n. Constructia incepe de la diagonala principala, apoi se construiesc coloanele.
Determinantul se numeste determinant HURWITZ si se noteaza Hn.
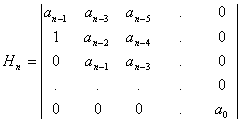
Fie 
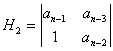
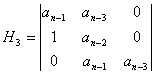
Minorii de NV extrasi din determinantul Hurwitz.
Criteriul Hurwitz are urmatorul enunt: Sistemul liniar in TC de polinom caracteristic (1) este intern asimptotic stabil daca si numai daca sunt indeplinite urmatoarele conditii:
toti coeficientii ai, i = 0, n-1 sunt pozitivi
determinantul Hurwitz si minorii sai de NV sunt strict pozitivi, adica:
Hj > 0; j=1,n
Aplicarea criteriului
Pasul 1 Determinarea polinomului caracteristic.
μ(s) = det(sI-A) pentru un sistem intrare - stare - iesire, sau H(s) dupa ce numitorul a fost adus in forma monica.
Pasul 2 Se verifica conditia 1.). Daca un coeficient este negativ sau lipseste nu mai are rost sa continuam.
Pasul 3 Se calculeaza determinantul Hurwitz si minorii acestuia si se verifica conditia 2.)
1.Exemplu:
H1 = 10,5 >0
H2 = 10,5 x 5,25 >0
Rezulta ca sistemul este asimptotic stabil (stabilitatea este asigurata la nivelul marimilor de stare).
2. Exemplu
Se considera multimea de sisteme avand polinomul caracteristic:
μ(s) = a2·s2+a1·s+a0, a0, a1, a2 au acelasi semn.
Sa se arate ca sistemele sunt intern asimptotic stabile.
In domeniul ingineriei reglarii in faza de proiectare se adopta o structura pentru sistemul de reglare, iar in cazul acestuia se adopta un tip de regulator. Parametrii regulatorului nu sunt cunoscuti. Problemele de proiectare constau in determinarea lor. O cerinta de proiectare este ca sistemul sa fie stabil. Se numeste domeniu de stabilitate domeniul parametrilor regulatorului pentru care sistemul este stabil. Odata determinat domeniul de stabilitate, proiectarea consta in stabilirea acelor valori din domeniu pentru care se asigura alte performante pentru sistemele de reglare. Ilustram cele de mai sus pana la detrminarea domeniului de stabilitate.
3. Exemplu.
Criteriul de stabilitate Routh
In 1877 Routh si in 1895 Hurwitz au publicat metode de analiza a stabilitatii solutiilor ecuatiilor diferentiale pe baza cunoasterii coeficientilor acestor ecuatii.
Prima conditie formulata de Routh pentru ca toate radacinile reale ale ecuatiei caracteristice sa fie negative este ca toti coeficientii ecuatiei sa fie pozitivi.
Se considera ecuatia caracteristica:
Q(s) = an·sn +an-1·sn-1+ +a1·s +a0
an, an-1, , a0 sunt reali pozitivi
Se intocmeste urmatorul tabel al coeficientilor:
Pe prima linie:
an an-2 an-4
Pe a doua linie
an-1 an-3 an-5
Pe a treia linie
Pe a patra linie
Tabelul se completeaza pana la ultima linie care va avea un singur termen.
Routh a demonstrat ca partile reale ale tuturor radacinilor ecuatiei caracteristice sunt negative numai daca toate elementele primei coloane a tabelului de mai sus sunt diferite de zero si au acelasi semn.
Exemplu:
Q(s) = s6 + 5·s5 + 9·s4 + 10·s3 + 11·s2 + 10·s + 3
S6 1 9 11
S5 5 10 10
S4 7 9 0
S3 5/7 11/7 0
S2 -6,4 3
S1 13,3
S0 3
Se constata ca nu toti termenii de pe prima coloana sunt pozitivi. Exista doua schimbari de semn: de la 5/7 la -6,4 si de la -6,4 la 13,3.
Sistemul nu este stabil.
Cand coeficentii unei linii sunt nuli ecuatia caracteristica admite radacini imaginare conjugate, adica sistemul este oscilant.
Exemplu:
Q(s) = s4 + s3 + 5·s2 + 4·s + 4
S4 1 5 4
S3 1 4 0
S2 1 4 0
S1 0 0
S0
Sistemul este oscilant
Criteriul lui Jury
Este un criteriu algebric si se refera la STD
Fie un STD cu polinomul caracteristic:
μ(z)= an·zn + an-1·zn-1 + . + a1·z + a0 (1)
Pornind de la polinomul caracteristic (1) se construieste o schema de calcul numita schema Jury.
Aceasta contine n-1 perechi de linii. In cadrul fiecarei perechi ce-a de-a doua linie reproduce pe prima linie in sens opus.
a0 a1 a2 an-1 an Prima pereche de linii
b2 an an-1 an-2 a1 a0
- j31 j32 j33 j3,n-1 j3,n A doua pereche de linii
b4 j41 j42 j43 j4,n-1 j4,n
j41 = j3,n
j42 = j3,n-1
Pe prima linie a primei perechi se plaseaza coeficientii caracteristici in ordine crescatoare a indicilor.
Fiecarei perechi de linii i se asociaza in
stanga barei un coeficeint numit coeficientul Jury care se calculeaza cu formula:
(2)
Incepand cu prima linie a celei de-a doua perechi de linii coeficientul primei linii se calculeaza cu formula:
-
j2k+1,i
Pe baza acestei scheme de calcul fiecare noua pereche de linii are un element mai putin decat perechea anterioara. Ca urmare pe ultima pereche de linii vom avea 2 elemente pe fiecare linie.
Criteriul Jury are urmatorul enunt:
Un STD de polinom caracteristic (2) este intern asimptotic stabil daca si numai daca sunt indeplinite urmatoarele conditii:
μ(1) > 0, valoare numerica a polinomului carcateristic
(-1)n μ(-1) > 0
, pentru k= 1,n-1
Exemplu
Sa se analizeze stabilitatea sistemului cu polinomul caracteristic:
μ(z) = 5·z3+2·z2-0,5·z +1
μ(1) = 7,5 > 0
(-1)3 μ(-1) = 1,5 > 0
1 -0,5 2 5
5 2 -0,5 1 -0,5 - 2 · 0,2
= 0,9
1/5=0,2 -0,9 2,1 4,8
-0,9/4,8 4,8 2,1 -0,9
Sistemul este intern asimptotic stabil.
|
