DREAPTA IN PLAN

  DREAPTA ÎN PLAN

Sistem de axe ortogonale: axa Ox este axa absciselor , iar axa Oy este axa ordonatelor.

  y 

  A

 

  B

 

  x

   

    O  

 

 

      C

   

Punctele A,B,C au coordonatele

Distanta dintre doua puncte: .

1. Coordonatele punctului P care împarte segmentul AB în raportul k : .
2. Daca , gasim coordonatele mijlocului M al unui segment AB : .
3. Centrul de greutate G al unui triunghi ABC : .

Ecuatia generala a unei drepte: (forma implicita) sau

  (forma explicita) .

Definitie este coeficientul unghiular al dreptei ( se mai numeste panta sau directia dreptei ).

Obs. m este tangenta unghiului format de dreapta cu axa Ox .

Ordonata la origine (intersectia cu axa Oy ) : .

Panta unui segment AB :

Drepte particulare :

• ecuatia axei Oy ;
• ecuatia axei Ox ;
• prima bisectoare a planului ;
• a doua bisectoare a planului ;
• o dreapta paralela cu axa Oy ;
• o dreapta paralela cu axa Ox ;
• o dreapta care trece prin originea axelor de coordonate .

Obtinerea ecuatiei dreptei :

1. Ecuatia dreptei prin taieturi ( dreapta care taie axele de coordonate în punctele si ) :   

.

2. Ecuatia dreptei care trece prin punctul si are panta m :

.

3. Ecuatia dreptei care trece prin doua puncte si  : 

sau sau

.

4. Ecuatia dreptei OA ( O fiind originea axelor de coordonate si ) : 

.

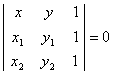Fie doua drepte si .

• Conditia ca dreptele si sa fie concurente : 

. 

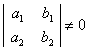Intersectia a doua drepte se afla prin rezolvarea sistemului format de ecuatiile celor doua drepte.

• Conditia ca doua drepte si sa fie paralele :

. 

Pantele celor doua drepte trebuie sa fie egale .

• Conditia ca doua drepte si sa fie perpendiculare :   

. 

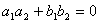Produsul pantelor celor doua drepte trebuie sa fie egal cu

sau .

Conditia ca doua drepte si sa fie confundate este ca coeficientii sa fie proportionali :

sau si .

• Conditia ca trei drepte sa fie concurente :   

.

1. Ecuatia unei normale (perpendiculare) la o dreapta d : este

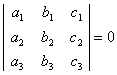
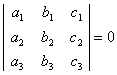( dreapta perpendiculara pe d ): , unde este arbitrar .

2. Ecuatiile bisectoarelor unghiurilor formate de doua drepte

: si : :   

.

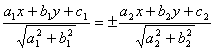Fascicole de drepte:

• Ecuatia fascicolului de drepte care trece prin punctul : 

, l fiind un parametru real .

• Ecuatia fascicolului de drepte paralele, de panta m : 

, l fiind un parametru real .

• Ecuatia fascicolului de drepte care trece prin intersectia a doua drepte si :

l fiind un parametru real .

1. Distanta de la punctul la o dreapta d :  :   

.

2. Aria triunghiului determinat de punctele A, B, C :   

, unde .

3. Conditia ca trei puncte A,B,C sa fie coliniare : 

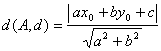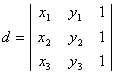, unde .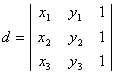

Unghiul a doua drepte este :

Punctele A,B,C au coordonatele

Distanta dintre doua puncte în plan : .

Distanta dintre doua puncte în spatiu : .

Ecuatiile planului

Ecuatia generala a planului în spatiul tridimensional este :

  , unde a, b, c nu sunt toate nule

Ecuatia planului care trece prin punctul este

 

Ecuatia planului care trece prin 3 puncte necoliniare este

 

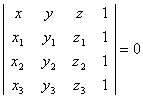
Conditia de necoliniaritate a 3 puncte este

 

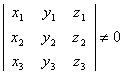
Conditia de intersectie a doua plane

Doua plane : si se intersecteaza dupa o dreapta

daca sau sau .

Ecuatiile dreptei în spatiu

Ecuatiile parametrice ale dreptei determinata de punctul si vectorul director sunt

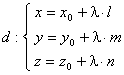unde .

Dreapta determinata de punctul si de vectorul director poate fi descrisa prin ecuatiile

canonice :

Fie punctele . Ecuatiile canonice ale dreptei care trece prin punctele A si B sunt :

 

Fie dreptele si date prin ecuatiile canonice :

si

Unghiul dintre doua drepte

Unghiul format de dreptele si este dat de formula :

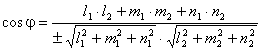
Pozitia relativa a unei drepte fata de un plan

Fie dreapta si planul .

1) Daca atunci d intersecteaza planul într-un punct . ‌‌

2) Daca si , atunci d‌‌‌‌ .

3) Daca si , atunci ‌ .

Unghiul format de o dreapta cu un plan

Fie dreapta si planul . Daca este unghiul

dintre dreapta d si planul atunci :

  .

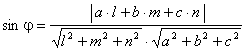Distanta de la un punct la un plan

Distanta de la un punct la planul este :

 

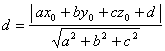
Unghiul dintre doua plane

Planele de ecuatii si au cosinusul unghiului dat

de formula :

.

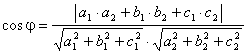Conditia de paralelism dintre doua plane

Planele de ecuatii si sunt paralele daca

( si , si , si pot fi simultan nule )

Aria unui triunghi cu vîrfurile

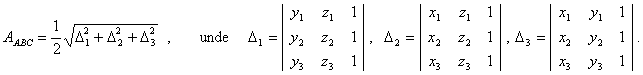
Volumul tetraedrului cu vîrfurile

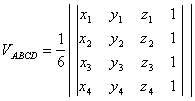( din modulul determinantului )

CERCUL

Ecuatia cercului cu centrul în origine si de raza r  Ecuatiile parametrice

 

Ecuatia cercului cu centrul în punctul si de raza r Ecuatiile parametrice

 

Ecuatia tangentei la cerc în punctul este

sau

Ecuatia tangentei se obtine din ecuatia cercului prin dedublare

ELIPSA

Ecuatia elipsei  Ecuatiile parametrice

 

Ecuatia tangentei la elipsa în punctul este

PARABOLA

Ecuatia parabolei cu axa de simetrie

Ecuatia parabolei cu axa de simetrie

Ecuatia tangentei la parabola în punctul este sau

 

HIPERBOLA

Ecuatia hiperbolei

Ecuatia tangentei la hiperbola în punctul este

Pentru a studia pozitia unei drepte fata de o conica, rezolvam sistemul format din ecuatia dreptei si ecuatia

conicei, ceea ce, prin substitutie, este echivalent cu rezolvarea unei ecuatii de grad mai mic sau egal cu 2 .

Pentru a determina eventualele puncte de intersectie ale unei conice cu o alta conica, rezolvam sistemul

format din ecuatiile celor doua conice .

RELAŢII METRICE ÎN PLAN sI ÎN SPAŢIU

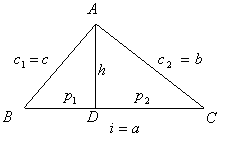
1. TRIUNGHIUL DREPTUNGHIC

Teorema lui PITAGORA

Numere pitagorice :  multipli

  1) 3, 4, 5 6, 8, 10 9, 12, 15 12, 16, 20 15, 20, 25

2) 5, 12, 13 10, 24,26 .  . .

3) 7, 24, 25 14, 48, 50 .  . .

4) 8, 15, 17 16, 30, 34 . . .

5) 9, 40, 41 18, 80, 82 .  . .

Proprietate

Daca este un triplet pitagoric, atunci si este un triplet pitagoric

Teorema catetei

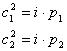unde

Teorema înaltimii ( 1 )  Teorema înaltimii ( 2 )

 

Altfel spus : daca laturile triunghiului dreptunghic sunt a, b si c adica atunci 

Aria triunghiului dreptunghic

2. TRIUNGHIUL ECHILATERAL

3. TRIUNGHIUL OARECARE

Teorema sinusurilor

Fie R raza cercului circumscris

Teorema cosinusului ( Teorema lui PITAGORA generalizata

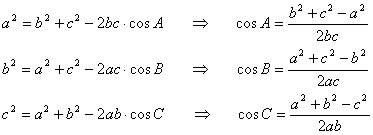
Aria triunghiului

1.

2.

3. formula lui HERON

4.

5.

Relatia medianei într-un triunghi

Relatia înaltimii

idem

NUMERE COMPLEXE

Un numar complex este de forma

OPERAŢII CU NUMERE COMPLEXE

Fie si . Atunci

NUMERE COMPLEXE CONJUGATE

se numeste conjugatul numarului complex

Proprietati

1)   2)

3)   4)

Fie si . Atunci

5) cu generalizarea .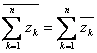

6) cu generalizarea .

7) 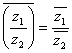  8)

MODULUL UNUI NUMĂR COMPLEX

Fie

Proprietati

1)   2)

3)   4)

5)   6)

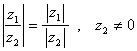
7) inegalitatea triunghiului

FORMA TRIGONOMETRICĂ A UNUI NUMĂR COMPLEX

Fie Atunci exista si sunt unice numerele reale si

astfel încît

Fie si . Atunci

Formula lui MOIVRE

.

TRIGONOMETRIE

Periodicitatea

Paritatea si imparitatea

Functii impare :   Functii pare :

 

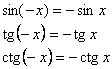
Formula fundamentalǎ a trigonometrie :

Formule ( mai greu de tinut minte )

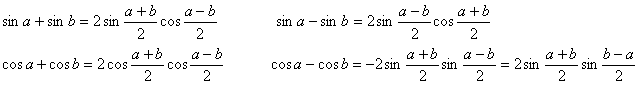
Daca notam atunci

 

LIMITE FUNDAMENTALE LA sIRURI

1)

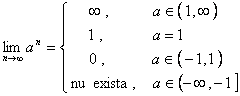
2)

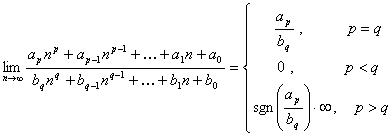
3)  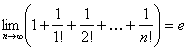 ( mai putin întîlnita )

4)

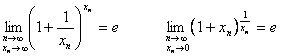
5)

6)

6)

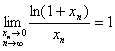
7)

LIMITE FUNDAMENTALE LA FUNCŢII

1)  

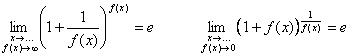
2)

3)

4)

5)

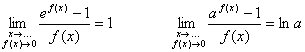
CRITERIUL RAPORTULUI

Fie un sir de numere reale strict pozitive pentru care exista

 

1) Daca atunci sirul este convergent si

2) Daca atunci

Observatie

Teorema nu da nici o indicatie asupra naturii sirului daca ( limita poate fi 0, finita sau ) .

CRITERIU DE CONVERGENŢĂ

Fie un sir de numere reale pentru care exista .

1) Daca atunci

2) Daca atunci

Observatie

Teorema nu da nici o indicatie asupra naturii sirului daca ( limita poate fi finita sau infinita ) .

CRITERIUL LUI STOLZ-CESARO

Fie si doua siruri de numere reale care au urmatoarele proprietati :

1) este un sir de numere pozitive, strict crescator si nemarginit adica

2) exista .

Atunci sirul 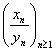are limita si

Observatie

Cu alte cuvinte, daca avem de calculat limita si , calculam limita care este

mai simpla si

CONSECINŢA 1 ( CRITERIUL MEDIEI ARITMETICE )

Fie un sir de numere reale care are limita . Atunci

 

CONSECINŢA 2 ( CRITERIUL MEDIEI GEOMETRICE )

Fie un sir de numere reale pozitive care are limita . Atunci

 

CONSECINŢA 3 ( CRITERIUL MEDIEI ARMONICE )

Fie un sir de numere reale pozitive care are limita . Atunci

 

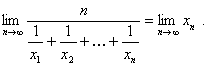
CONSECINŢA 4 ( CRITERIUL RAPORTULUI )

Fie un sir de numere reale pozitive care are limita . Daca sirul 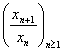are limita atunci

 

sIRUL LUI e

Fie Atunci sirul este strict crescator si marginit, deci convergent . Limita se

noteaza cu e si avem

COROLAR

sirul este strict crescator, iar sirul este strict descrescator si avem

inegalitatile :

Observatie

Numarul e (initiala de la Euler) este irational (transcendent) si avem

TEOREMĂ

sirul este strict crescator si are limita e .

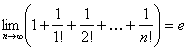
TEOREMA LUI ROLLE

Fie o functie care îndeplineste conditiile :

1) este continua pe

2) este derivabila pe

3)

Atunci exista cel putin un punct astfel încît

CONSECINŢĂ

Între doua radacini ale unei functii derivabile pe un interval se gaseste cel putin o radacina a derivatei .

TEOREMA LUI LAGRANGE

Fie o functie care îndeplineste conditiile :

1) este continua pe

2) este derivabila pe .

Atunci exista cel putin un punct astfel încît

sIRUL LUI ROLLE

O problema importanta în rezolvarea unei ecuatii de forma , unde f este o functie reala de

argument real, o reprezinta separarea radacinilor reale ale acesteia .

Separarea solutiilor ecuatiei presupune :

a) determinarea numarului de solutii reale ale ecuatiei ;

b) precizarea intervalelor în care aceste solutii sunt situate .

Teorema lui Rolle si consecintele acesteia permit stabilirea unei metode de separare a solutiilor reale ale

unor ecuatii, metoda cunoscuta sub numele de "sirul lui Rolle".

Aceasta metoda se aplica în general pentru ecuatii de forma