ALTE DOCUMENTE
|
||||||||||
ELEMENTE DE TEORIA PROBABILITATILOR
Experiment. Eveniment
Experiment (proba) - orice realizare a unui complex de conditii bine precizate.
In teoria statistica, dupa natura conditiilor in care se desfasoara experimentul, deosebim:
- experimente deterministe, caz in care conditiile definesc in mod ce 727e48h rt rezultatele posibile;
- experimente aleatoare, cand conditiile nu genereaza, in mod cert, rezultatele.
Un experiment aleator se caracterizeaza prin aceea ca:
- nu are caracter determinist, adica in conditii identice de realizare, rezultatele experimentului pot fi diferite;
- are un caracter statistic, adica exista o stabilitate a frecventelor rezultatelor - cu cat numarul repetarilor experimentului creste, frecvanta cu care se produce un anume rezultat se gaseste in jurul unei valori, valoare ce reprezinta sansa de realizare a sa.
Eveniment - orice situatie legata de o experienta aleatoare, despre care se poate spune cu certitudine ca s-a realizat sau nu.
Eveniment simplu (elementar) - evenimentul care se poate realiza dintr-o singura proba.
Eveniment compus - formeaza partitii cu cel putin doua elemente simple.
Fiecarei experiente aleatoare i se asociaza, intodeauna, doua evenimente:
evenimentul sigur (evenimentul care se realizeaza prin fiecare din probele experientei), notat cu Ω;
evenimentul imposibil (evenimentul care nu se realizeaza, oricare ar fi proba experientei), notat cu Ф.
Alte clase de evenimente legate de o experienta aleatoare:
- evenimente contrare (complementare) - daca nerealizarea unuia implica realizarea celuilalt.
Notatie: A (sau CA)
- evenimente incompatibile (disjuncte) - daca nu exista cazuri (probe) favorabile realizarii lor simultane.
- evenimente compatibile - daca exista cazuri (probe) prin care se realizeaza simultan.
Evenimente independente
Definitie: Doua evenimente A,B![]() se numesc independente daca realizarea unuia nu este conditionata de realizarea
celuilalt, adica
se numesc independente daca realizarea unuia nu este conditionata de realizarea
celuilalt, adica
P(A|B)=P(A), daca
P(B)![]() 0 si
0 si
P(B|A)=P(B), daca
P(A) ![]() 0.
0.
In caz contrar ele se numesc dependente.
Observatie: Din formulele P(A|B) si P(B|A) rezulta:
P(A![]() B) P(A) P(B)
B) P(A) P(B)![]() A, B independente. Relatia devine valabila si pentru cazul general cu
evenimentele
A, B independente. Relatia devine valabila si pentru cazul general cu
evenimentele ![]() ,
independente doua cate doua
,
independente doua cate doua ![]() ,
,
![]()
![]() ,
astfel:
,
astfel:
![]()
Camp de evenimente
Definitie: O familie (![]() )
de submultimi ale lui
)
de submultimi ale lui ![]() (
(![]()
![]() P(
P(![]() ))
cu:
))
cu:
i) ![]()
ii) ![]() ,
I cel mult numarabila se numeste:
,
I cel mult numarabila se numeste:
- corp de parti - daca I este finita
- ![]() -corp
de parti (corp borelian) - daca I
este infinita
-corp
de parti (corp borelian) - daca I
este infinita
Perechea (![]() )
se numeste camp (
)
se numeste camp (![]() -camp)
de evenimente sau spatiu probabilizabil.
-camp)
de evenimente sau spatiu probabilizabil.
Observatie: Orice ![]() -corp
de parti este un corp de parti.
-corp
de parti este un corp de parti.
Definitie: Un sistem de evenimente ![]() se numeste sistem complet de evenimente daca S
este o partitie din
se numeste sistem complet de evenimente daca S
este o partitie din ![]() .
.
Operatii cu evenimente
a) Reuniunea a doua evenimente A si B
(notat A ![]() B)
B)
Reprezinta evenimentul a carei realizare consta in realizarea a cel putin uneia dintre evenimentele A, B.
b) Intersectia a doua evenimente A si
B (notat cu A![]() B).
B).
Presupune realizarea simultana a celor doua evenimente.
Observatie :
Cele doua operatii de mai sus se pot
extinde la cazul unei familii de evenimente iєI
, I cel mult numarabila. Deci,
putem considera ![]() si
si ![]()
![]() cu
semnificatia:
cu
semnificatia:
![]() - este evenimentul care consta in realizarea cel putin a unuia
dintre evenimentele Ai , i
- este evenimentul care consta in realizarea cel putin a unuia
dintre evenimentele Ai , i![]() I;
I;
![]() - este evenimentul care consta in realizarea
simultana a tuturor evenimentelor Ai ,
- este evenimentul care consta in realizarea
simultana a tuturor evenimentelor Ai , ![]() i
i![]() I;
I;
c) Diferenta a doua evenimente A si B (notat AB).
Este evenimentul a carui realizare consta in realizarea evenimentului A si nerealizarea evenimentului B.
d) Operatia "non".
Evenimentul non A (notat si A) este evenimentul realizat de
orice proba a experientei, care nu realizeaza evenimentul A. A se mai numeste si contrarul lui A sau opusul lui A. Doua
evenimente A si B cu A∩B = Ø
sunt incompatibile si disjuncte, iar daca A![]() B
≠ Ø sunt compatibile.
B
≠ Ø sunt compatibile.
Probabilitate
5.1.Definitia statistica a probabilitatii
Fie E o experienta aleatoare careia i se asociaza
campul de evenimente (![]() )
si
)
si ![]() .
Daca experienta E se repeta de n ori, raportul
.
Daca experienta E se repeta de n ori, raportul
fn(A) (nr. de realizari ale evenimentului A)/n
se numeste frecventa relativa a lui A.
Cand n creste, ![]() tinde sa se stabilizeze catre un numar, numit
probabilitatea lui A, adica P(A). Deci P(A)
tinde sa se stabilizeze catre un numar, numit
probabilitatea lui A, adica P(A). Deci P(A)![]()
5.2. Definitia clasica a probabilitatii
Se presupune ca (![]() )
este un camp finit de evenimente. Pentru
)
este un camp finit de evenimente. Pentru ![]() avem:
avem:
P(A)![]() (numarul
cazurilor favorabile evenimentului A)/(numarul cazurilor posibile)
(numarul
cazurilor favorabile evenimentului A)/(numarul cazurilor posibile)
5.3Definitia axiomatica a probabilitatii (Kolmogorov, 1933)
Definitie:
Fiind dat (![]() )
un camp de evenimente, o functie
)
un camp de evenimente, o functie ![]() ce are proprietatile:
ce are proprietatile:
i)
P(![]() )=1
)=1
ii)
P![]() ,
I cel mult numarabila,
,
I cel mult numarabila, ![]() cu
cu ![]() ,
,
![]() ,
,
![]() se numeste probabilitate pe
se numeste probabilitate pe ![]() .
.
6. Camp de probabilitate
Definitie: Un triplet (![]() ),
in care:
),
in care:
i) ![]() este o multime abstracta reprezentand multimea
evenimentelor elementare ale unui experiment;
este o multime abstracta reprezentand multimea
evenimentelor elementare ale unui experiment;
ii) ![]() este un corp borelian pe
este un corp borelian pe ![]() (
(![]() );
);
iii) P este o
probabilitate pe ![]() ,
unde P(A) reprezinta sansa de realizare a evenimentului
,
unde P(A) reprezinta sansa de realizare a evenimentului ![]() ,
,
se numeste camp
(sau ![]() -camp)
de probabilitate, dupa cum (
-camp)
de probabilitate, dupa cum (![]() )
este camp sau
)
este camp sau ![]() -camp
de evenimente.
-camp
de evenimente.
Nota: ![]() -camp
de probabilitate se mai numeste camp borelian de probabilitate.
-camp
de probabilitate se mai numeste camp borelian de probabilitate.
Probabilitati conditionate
Fie (![]() P) si A,B
P) si A,B![]() cu P(B)
cu P(B)![]() .
.
Definitie: Numarul P(A|B) sau ![]() definit prin P(A|B)
definit prin P(A|B)![]() se numeste probabilitatea evenimentului A conditionata de B (sau probabilitatea
lui A in ipoteza ca a avut loc B).
se numeste probabilitatea evenimentului A conditionata de B (sau probabilitatea
lui A in ipoteza ca a avut loc B).
Observatia 1: P(B|A) sau ![]()
P(A|B)![]() P(B|A)
P(B|A)
Din 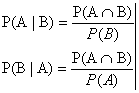
![]() P(A
P(A![]() B)
B)
![]() (1)
(1)
Relatia (1) se poate generaliza pentru n evenimente astfel:
![]()
Observatia 2: Daca Ai,
![]() sunt evenimente incompatibile doua cate doua,
atunci pentru orice eveniment B avem:
sunt evenimente incompatibile doua cate doua,
atunci pentru orice eveniment B avem:

8. Formule clasice de probabilitate
Fie (![]() K, P) un camp de probabilitate.
K, P) un camp de probabilitate.
Propozitia 1. (Probabilitatea reuniunii de evenimente)
Fie ![]() K,
i=
K,
i=![]()

se numeste formula lui Poicaré.
Observatie. Daca evenimentele sunt incompatibile, formula lui Poicaré se scrie:


Propozitia 2. (Probabilitatea unei intersectii de evenimente)
Daca evenimentele ![]() K, i=
K, i=![]() sunt astfel incat
sunt astfel incat
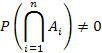
atunci:

Observatie. Daca
evenimentele ![]() K, i=
K, i=![]() sunt independente, atunci:
sunt independente, atunci:
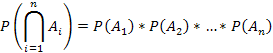
se numeste formula de inmultire a probabilitatilor.
Propozitia 3. (Inegalitatea lui Boole)
Fie ![]() K. Atunci are loc inegalitatea:
K. Atunci are loc inegalitatea:

Propozitia 4. (Formula probabilitatii totale)
Fie ![]() K este un sistem complet de evenimente pe
K este un sistem complet de evenimente pe ![]() K), atunci pentru
K), atunci pentru ![]() A
A![]() K avem:
K avem:
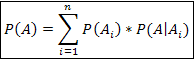
Propozitia 5. (Formula lui Bayes sau Probabilitatea ipotezelor)
Pentru aceleasi date ca la Propozitia 4 avem:
![]()
Observatie.
Probabilitatile P(![]() ),
i=
),
i=![]() se numesc probabilitati apriori.
se numesc probabilitati apriori.
Probabilitatile P(![]() )
se numesc probabilitati a posteriori.
)
se numesc probabilitati a posteriori.
Formula
lui Bayes permite gasirea P(![]() )
conditionata de realizarea evenimentului A, adica a probabilitatii cauzei
(ipotezei) ce a dus la aparitia evenimentului A.
)
conditionata de realizarea evenimentului A, adica a probabilitatii cauzei
(ipotezei) ce a dus la aparitia evenimentului A.
9. VARIABILE ALEATOARE
Variabila aleatoare reprezinta o marime care - drept rezultat al unui experiment - poate lua o valoare oarecare, fara sa se poata preciza dinainte care anume.
Dupa numarul de valori ale variabilei X, distingem:
variabile aleatoare cu un numar finit de valori: X=;
variabile aleatoare cu un numar infinit de valori discrete
X
variabile aleatoare cu un numar infinit nenumarabil de valori
X=[a,b] ![]() R.
R.
![]() discreta , daca X are un numar finit
discreta , daca X are un numar finit
sau numarabil de evenimente
 Variabila aleatoare
Variabila aleatoare
continua, daca X are un numar infinit
si nenumarabil de elemente
Repartitia unei variabile aleatoare discrete
X : ![]()
![]()
![]() pe scurt X
:
pe scurt X
: ![]() i
i![]()
Se observa ca o variabila aleatoare
discreta X se da prezentand valorile sale ![]() ,
, ![]() si odata cu acestea probabilitatile
si odata cu acestea probabilitatile ![]() ,
, ![]() ,
corespunzatoare (
,
corespunzatoare (![]() este probabilitatea ca variabila aleatoare X
sa ia valori
este probabilitatea ca variabila aleatoare X
sa ia valori ![]() , adica
, adica ![]() =P(X=
=P(X=![]() ),
i
),
i![]() .
.
Functia de repartitie a variabilei aleatoare X se defineste prin
F(x)=P(X<x)
si indica probabilitatea ca valoarea variabilei X sa fie inferioara unei valori date.
Din punct de vedere probabilistic, functia de repartitie caracterizeaza, in general, complet o variabila aleatoare, indiferent daca este vorba de o variabila aleatoare discreta sau continua.
Se cunoaste ca:
daca ![]() atunci F(x
atunci F(x![]() )
)![]() F(x
F(x![]() )
)
F(![]() )
=0
)
=0
F(![]() )
=0
)
=0
0![]() F(x)
F(x)![]()
Graficul functiei de repartitie
a) cazul variabilei aleatoare discreta
![]() y
y
y=
----- ----- ----------------(----- ----- -----
![]() ( ]
( ]
![]() ( ]
( ]
![]() x
x
Se observa ca graficul este format din segmente paralele cu ![]()
b) cazul variabilei aleatoare continua
![]() y
y
y=1
-------- ----- ------ ---------
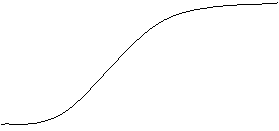
![]() x
x
Densitatea de repartitie (de probabilitate) a variabilei aleatoare X
f(x)=F'(x)
Functia f(x), prima derivata a functiei de repartitie, are semnificatia unei caracteristici a densitatii cu care se repartizeaza valorile variabilei aleatoare in punctul dat.
Exprimarea functiei de repartitie prin densitatea de repartitie:
F(x)=![]()
Se cunoaste ca:
f(x)![]()
![]()
 , adica probabilitatea ca
variabila aleatoare continua X sa ia
valoare in intervalul (a,b) este
egala cu integrala densitatii de repartitie pe intervalul (a,b).
, adica probabilitatea ca
variabila aleatoare continua X sa ia
valoare in intervalul (a,b) este
egala cu integrala densitatii de repartitie pe intervalul (a,b).
Caracteristici numerice ale variabilelor aleatoare
Daca variabila aleatoare X este discreta consideram X :![]() i
i![]() I,
iar daca X este continua cu
densitatea de repartitie f consideram
I,
iar daca X este continua cu
densitatea de repartitie f consideram
X: ![]() x
x ![]() R.
R.
Media - M(X)
Pentru orice variabila aleatoare X avem:
 , in cazul discret
, in cazul discret
M(X)=
, in cazul continuu
Proprietatile mediei:
M(a) = a, (![]() )
a
)
a![]() R
R
M(aX)= a M(X)
M(X+Y)=M(X)+M(Y)
M(XY)=M(X) M(Y)
. Momentul (initial) de ordin k , k![]() -
- ![]()
Mk (X) = M(Xk)
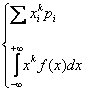
, in cazul discret
![]()
, in cazul continuu
Obs. Media variabilei aleatoare X reprezinta momentul (initial) de ordin 1 al variabilei aleatoare X.
Momentul
centrat de ordin k, k![]() -
- ![]()
![]() =
=![]() = M(X-M(X))k
= M(X-M(X))k
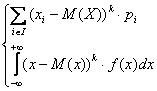
, in cazul discret
![]()
, in cazul continuu
Dispersia - ![]()
![]() =
=![]() =
M(X-M(X))2
=
M(X-M(X))2

, in cazul discret
![]()
, in cazul continuu
Proprietatile dispersiei:
- ![]() , (
, (![]() )
a
)
a![]() R
R
- ![]()
- ![]()
Abaterea medie patratica - D(X)
D(X)=![]()
Covarianta si coeficientul de corelatie a doua variabile aleatoare
![]()
Proprietatile covariantei :
cov (X,Y)= cov(Y,X)
cov(![]() X,
X,![]() Y)=
Y)=![]() cov(X,Y)
cov(X,Y)
cov (X,Y)=
M(XY) - ![]()
Coeficientul de corelatie al variabilelor X si Y - r(X,Y):
r (X,Y)=![]()
Observatii:
1![]() .
.
![]() intre
X si Y exista o relatie liniara
intre
X si Y exista o relatie liniara
2![]() .
Daca cov (X,Y)=0
.
Daca cov (X,Y)=0 ![]() variabilele aleatoare X si Y se numesc
necorelate.
variabilele aleatoare X si Y se numesc
necorelate.
2.5 LEGI DE PROBABILITATE CLASICE
O lege de probabilitate se caracterizeaza prin faptul ca oricarei valori pe care o ia o variabila aleatoare i se asociaza o probabilitate corespunzatoare si numai una.
1. Repartitia normala
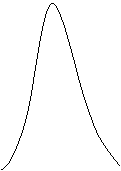
Reprezinta legea de repartitie cea mai importanta din teoria probabilitatilor, fiind denumita si legea lui Gauss.
Fie X
o variabila aleatoare continua care urmeaza o repartitie normala de medie m si abaterea standard ![]() atunci densitatea de probabilitate este :
atunci densitatea de probabilitate este :
f: R![]() , f(x)=
, f(x)=
Caracteristici:
M(X)=m
![]()
Graficul functiei f(x)
x![]() R,
are forma unui clopot (clopotul
lui Gauss) si este simetric fata de dreapta x=m.
R,
are forma unui clopot (clopotul
lui Gauss) si este simetric fata de dreapta x=m.
Punctul ![]() este
punctul de maxim, f(m)=
este
punctul de maxim, f(m)=![]() ,
iar punctele
,
iar punctele ![]() =
=![]() si
si ![]() =
=![]() sunt puncte de inflexiune pentru graficul functiei f(x).
sunt puncte de inflexiune pentru graficul functiei f(x).
![]() f(x)
f(x)
![]()

![]() ------------
------------
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() x
x
m-![]() m m+
m m+![]()
Toate curbele
normale au forma de clopot, avand convexitatea indreptata in sus, in apropierea
punctului de maxim. In punctele m-![]() si m+
si m+![]() ele isi schimba
convexitatea si cu cat
ele isi schimba
convexitatea si cu cat ![]() este mai mic cu atat clopotul este
mai ascutit, iar cu cat
este mai mic cu atat clopotul este
mai ascutit, iar cu cat ![]() este mai mare cu atat clopotul
este mai turtit.
este mai mare cu atat clopotul
este mai turtit.
![]() f(x)
f(x)
![]()
 III
III
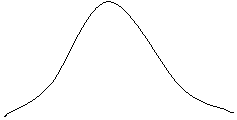
![]() II
II

![]() I
I
![]() x
x
In figura de mai
sus sunt ilustrate trei curbe normale (I, II, III), avand m=0 si dispersii diferite. Curba I corespunde celui mai mare![]() iar curba III, celui mai mic. Asadar, cei doi parametrii care
definesc curba de repartitie N (m,
iar curba III, celui mai mic. Asadar, cei doi parametrii care
definesc curba de repartitie N (m, ![]() au
o semnificatie bine precizata: m
defineste pozitia curbei fata de axa
au
o semnificatie bine precizata: m
defineste pozitia curbei fata de axa ![]() ,
iar
,
iar ![]() caracterizeaza dispersia
unitatilor populatiei, determinand deschiderea clopotului.
caracterizeaza dispersia
unitatilor populatiei, determinand deschiderea clopotului.
Obs. Daca X![]() ,
atunci X se numeste normal
distribuita si normata (sau variabila aleatoare normala standard).
,
atunci X se numeste normal
distribuita si normata (sau variabila aleatoare normala standard).
Pentru m=0 si ![]() =1 se obtine o forma particulara a
repartitiei normale numita repartitia normala normata. Densitatea de repartitie
a unei variabile aleatoare X
=1 se obtine o forma particulara a
repartitiei normale numita repartitia normala normata. Densitatea de repartitie
a unei variabile aleatoare X![]() N(0,1) este:
N(0,1) este:
f(x)=![]() ,
,![]() x
x![]() R
R
Repartitia hi-patrat (![]() )
)
Este utilizata,
in general, la construirea testelor statistice. Fie ![]() variabile independente, distribuite dupa o
lege normala standard. Atunci variabila obtinuta prin insumarea patratelor lor
variabile independente, distribuite dupa o
lege normala standard. Atunci variabila obtinuta prin insumarea patratelor lor ![]() =
= ![]() urmeaza o distributie
urmeaza o distributie![]() cu v grade de libertate, simbolizata cu
cu v grade de libertate, simbolizata cu![]() (v) .
(v) .
Densitatea de repartitie (de probabilitate) are forma:

x>0
f:R![]() [0,1] , f(x) =
[0,1] , f(x) =
, x![]()
unde  , a>0
este integrala Gamma a lui Euler.
, a>0
este integrala Gamma a lui Euler.
Caracteristicile repartitiei hi-patrat cu v grade de libertate:
![]()
![]()
Forma acestei repartitii depinde de numarul de grade de libertate, in sensul ca, pe masura ce v creste , alura curbei repartitiei se apropie de alura repartitiei normale, ca in figura de mai jos:
![]()
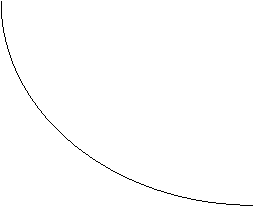
![]() (3)
(3)
![]() (5)
(5)

![]() (10)
(10)

![]()
![]() (20)
(20)
Repartitia ![]() se utilizeaza in principal pentru urmatoarele:
se utilizeaza in principal pentru urmatoarele:
construirea testelor de concordanta in ajustarea unei distributii empirice prin una teoretica;
testarea semnificatiei parametrilor functiei de regresie;
testarea independentei a doua caracteristici calitative;
in construirea intervalelor de incredere pentru parametrii unui model;
testele de comparare a mediilor pentru diverse populatii etc.
Repartitia Fisher - Snedecor
Fie X
si Y doua variabile aleatoare
independente care urmeaza distributiile de probabilitate ![]() (v
(v![]() )
, respectiv
)
, respectiv ![]() (v
(v![]() ).
).
Se defineste prin:
![]()
o variabila aleatoare ce urmeaza o lege
Fisher-Snedecor cu ![]() si
si ![]() grade de liberate.
grade de liberate.
Densitatea de probabilitate are forma:

f:R![]()
![]() , f(x)= , x
, f(x)= , x![]()
,x <0
Caracteristici principale:
![]() , daca
, daca ![]()
![]() ,
daca
,
daca ![]()
Legea ![]() se utilizeaza cel mai adesea pentru
construirea testelor statistice pentru analiza variantei si a covariantei.
se utilizeaza cel mai adesea pentru
construirea testelor statistice pentru analiza variantei si a covariantei.
Repartitia Student
Distributia Student, cunoscuta si sub denumirea de "repartitia t", afost descoperita de statisticianul englez Gosset (cunoscut sub pseudonimul "Student").
Fie doua variabile aleatoare X si Y . Daca X este distribuita dupa o distributie hi-patrat cu v grade de libertate, iar Y are o distributie normala standard , atunci variabila definita astfel:
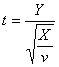
are o distributie Student (sau t) cu v grade libertate. Densitatea de probabilitate a acestei repartitii este:
f:R![]() , f(x)=
, f(x)=
unde  , a>0 este integrala Gamma a lui Enler.
, a>0 este integrala Gamma a lui Enler.
Caracteristicile variabilei t:
![]()
![]() , daca v>2
, daca v>2
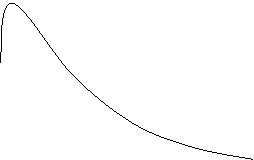
Densitatea de
probabilitate are graficul sub forma unui clopot simetric, forma graficului
fiind determinata de numarul gradelor de libertate. Cu cat v este mai mic, cu atat curba este mai aplatizata, iar daca v![]() graficul curbei Student tinde catre
graficul repartitiei normale.
graficul curbei Student tinde catre
graficul repartitiei normale.
![]() f(x)
f(x)
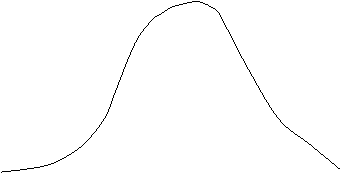
![]() v
v![]()
![]() v=5
v=5


![]() v=1
v=1
![]() x
x
-2 -1 0 1 2 3
Tabelele
repartitiei t dau valori pentru v![]() .
Plecand de la v>30, repartitia t devine
foarte apropiata de repartitia normala centrata redusa.
.
Plecand de la v>30, repartitia t devine
foarte apropiata de repartitia normala centrata redusa.
Repartitia Student este folosita in descrierea
distributiilor de selectie in cazul esantioanelor de volum mic (n<30) si
indeosebi, in verificarea ipotezelor statistice cu privire la media unei
populatii normale, cand parametrul ![]() este necunoscut.
este necunoscut.
|