Examen analiza - 31 ianuarie
2008- Seria CA
Prof. Radu Gologan Asist. Luminita Costache
1. Fie 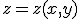 functie definita implicit de ecuatia
functie definita implicit de ecuatia 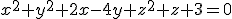 . Sa se studieze extremele acesteia.
. Sa se studieze extremele acesteia.
2. Calculati
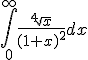 , folosind eventual o in 15415d322p tegrala Beta.
, folosind eventual o in 15415d322p tegrala Beta.
3. Sa se calculeze ca integrala cu parametru 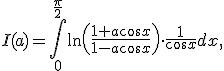 unde
unde 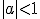
4. Sa se calculeze cu formula Green -Riemann
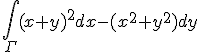 , unde
, unde 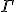 este sfertul de cerc
este sfertul de cerc 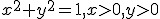
5. Sa se calculeze fluxul campului
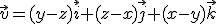
prin suprafata deschisa 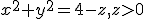 , utilizand
teorema Gauss-Ostrogradsky.
, utilizand
teorema Gauss-Ostrogradsky.
6. Folositi formula lui Taylor cu rest de ordin 1
(teorema de medie) pentru a demonstra urmatorul rezultat: Fie 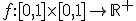 , diferentiabila cu
, diferentiabila cu 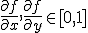 si
si 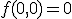 . Atunci
. Atunci 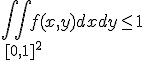
Refacere partial
1. Studiati convergenta uniforma a seriei
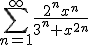
2. Calculati suma seriei
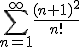
3. Sa se arate ca functia definita pe 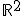 prin
prin 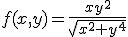 pentru
pentru 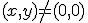 si
si 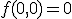 este diferentiabila , dar nu e de clasa
este diferentiabila , dar nu e de clasa 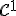 4.
Dezvoltati in serie Fourier
pe
4.
Dezvoltati in serie Fourier
pe 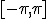 , functia
, functia 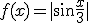
Examen analiza - 2 februarie 2008- Seria CA
Prof. Radu Gologan, Asist. Luminita
Costache
1. Sa se studieze extremele locale ale functiei 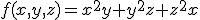 pe portiunea din planul
pe portiunea din planul 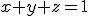 cu
cu 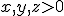 . Ce se schimba daca regiunea din planul de mai sus este
descrisa de
. Ce se schimba daca regiunea din planul de mai sus este
descrisa de 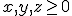
2. Calculati 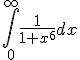 , folosind eventual o in 15415d322p tegrala Beta.
, folosind eventual o in 15415d322p tegrala Beta.
3. Sa se calculeze ca integrala cu parametru
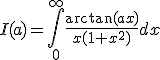 , unde
, unde 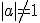
4. Sa se calculeze cu formula Green -Riemann
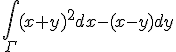 , unde
, unde 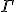 este cercul
este cercul 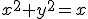
5. Sa se calculeze fluxul campului
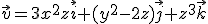
prin suprafata deschisa 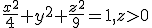 , utilizand teorema Gauss-Ostrogradsky.
, utilizand teorema Gauss-Ostrogradsky.
6. Fie 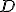 discul de centru O si raza
discul de centru O si raza 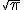 in
in
plan. Aratati ca
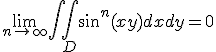
Refacere partial
1. Studiati convergenta seriei
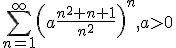
2. Studiati convergenta punctuala si uniforma a sirului
de functii
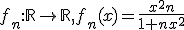
3. Dezvoltati in serie de puteri
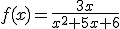 , precizand domeniul de definitie si domeniile de
convergenta punctuala , respectiv uniforma.
, precizand domeniul de definitie si domeniile de
convergenta punctuala , respectiv uniforma.
4. Fie 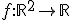 data prin
data prin 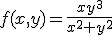 pentru
pentru 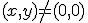 si
si 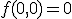 . Aratati ca
. Aratati ca 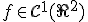
Calculati derivatele partiale de
ordinul 2 in origine.
Este 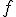 de clasa
de clasa 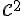
Examen analiza - 8 februarie 2008- Seria CA
Prof. Radu Gologan, Asist. Luminita Costache
1. Fie 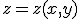 functie definita implicit de ecuatia
functie definita implicit de ecuatia 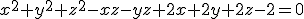 . Sa se studieze extremele acesteia. Sa se calculeze
. Sa se studieze extremele acesteia. Sa se calculeze 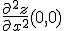
2. Calculati 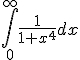 , folosind eventual o
, folosind eventual o
integrala Beta.
3. Sa se calculeze ca integrala cu parametru
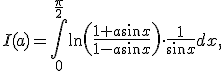 unde
unde 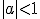
4. Sa se calculeze cu formula Green -Riemann
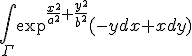
unde 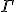 este sfertul de elipsa
este sfertul de elipsa 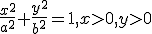
5. Sa se calculeze fluxul 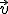
unde 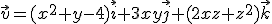
dupa normala exterioara , utilizand teorema lui Stokes,
pentru suprafata 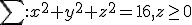
6. Fie 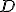 discul de centru O si raza 1 in plan. Aratati ca
discul de centru O si raza 1 in plan. Aratati ca 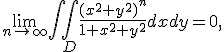
folosind eventual un disc de raza mai mica pe care
functia data converge uniform la 0.
Refacere partial
1. Studiati convergenta uniforma a seriei
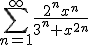
2. Calculati suma seriei
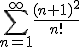
3. Dezvoltati in serie Fourier pe 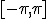 , functia
, functia 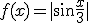
4. Fie 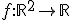 data prin
data prin 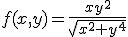 pentru
pentru 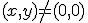 si
si 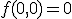 Aratati ca este diferentiabila dar nu
e de clasa
Aratati ca este diferentiabila dar nu
e de clasa 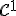 .
.
![]() functie definita implicit de ecuatia
functie definita implicit de ecuatia ![]() . Sa se studieze extremele acesteia.
. Sa se studieze extremele acesteia. 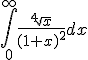 , folosind eventual o in 15415d322p tegrala Beta.
, folosind eventual o in 15415d322p tegrala Beta. 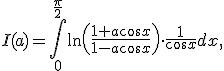 unde
unde ![]()
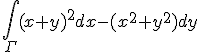 , unde
, unde ![]() este sfertul de cerc
este sfertul de cerc ![]()
![]()
![]() , utilizand
teorema Gauss-Ostrogradsky.
, utilizand
teorema Gauss-Ostrogradsky. ![]() , diferentiabila cu
, diferentiabila cu ![]() si
si ![]() . Atunci
. Atunci 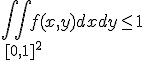
![]()
![]()
![]() prin
prin ![]() pentru
pentru ![]() si
si ![]() este diferentiabila , dar nu e de clasa
este diferentiabila , dar nu e de clasa ![]() 4.
Dezvoltati in serie Fourier
pe
4.
Dezvoltati in serie Fourier
pe ![]() , functia
, functia ![]()
![]() pe portiunea din planul
pe portiunea din planul ![]() cu
cu ![]() . Ce se schimba daca regiunea din planul de mai sus este
descrisa de
. Ce se schimba daca regiunea din planul de mai sus este
descrisa de ![]()
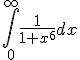 , folosind eventual o in 15415d322p tegrala Beta.
, folosind eventual o in 15415d322p tegrala Beta. 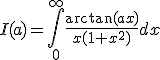 , unde
, unde ![]()
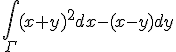 , unde
, unde ![]() este cercul
este cercul ![]()
![]()
![]() , utilizand teorema Gauss-Ostrogradsky.
, utilizand teorema Gauss-Ostrogradsky. ![]() discul de centru O si raza
discul de centru O si raza ![]() in
in 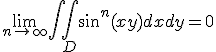
![]()
![]()
![]() , precizand domeniul de definitie si domeniile de
convergenta punctuala , respectiv uniforma.
, precizand domeniul de definitie si domeniile de
convergenta punctuala , respectiv uniforma. ![]() data prin
data prin ![]() pentru
pentru ![]() si
si ![]() . Aratati ca
. Aratati ca ![]()
![]() de clasa
de clasa ![]()
![]() functie definita implicit de ecuatia
functie definita implicit de ecuatia ![]() . Sa se studieze extremele acesteia. Sa se calculeze
. Sa se studieze extremele acesteia. Sa se calculeze ![]()
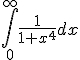 , folosind eventual o
, folosind eventual o 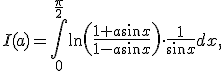 unde
unde ![]()
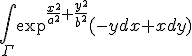
![]() este sfertul de elipsa
este sfertul de elipsa ![]()
![]()
![]()
![]()
![]() discul de centru O si raza 1 in plan. Aratati ca
discul de centru O si raza 1 in plan. Aratati ca 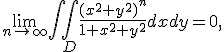
![]()
![]()
![]() , functia
, functia ![]()
![]() data prin
data prin ![]() pentru
pentru ![]() si
si ![]() Aratati ca este diferentiabila dar nu
e de clasa
Aratati ca este diferentiabila dar nu
e de clasa ![]() .
.