FUNCTIA DE GRADUL II

Reprezentarea grafica a functiei

f : R R, f(x) = ax²+bx+c, a,b,cIR, a 0, intersectia graficului cu axele de coordonate, ecuatia f(x)=0, simetria fata de drepte de forma x = m, mIR .

Relatiile lui Viet 717d35h e,

rezolvarea sistemelor de forma s,pIR.

Monotonie. Studiul monotoniei prin semnul diferentei f(x₁) – f(x₂), rata cresterii (descresterii) , IR, , punct de extrem, (varful parabolei).

Pozitia relativa a unei drepte fata de o parabola: rezolvarea sistemelor de forma a, b, c, m, nIR

Rezolvarea sistemelor de forma , a₁, a₂, b₁, b₂, c₁, c₂IR, interpretare geometrica

f:R R f(x)=ax²+bx+c

Graficul functiei de gradul II

Graficul e o parabola :-daca a>0 parabola e convexa

-daca a<0 parabola e concava

G_f Ox se determina rezolvand ecuatia f(x)=0 :-daca D>0 ecuatia are doua radacini deci graficul taie axa Ox in doua puncte A(x₁,0) si B(x₂,0)

-daca D=0 ecuatia are o radacina deci graficul taie Ox intr-un singur punct A(x₁,0)

-daca D<0 ecuatia nu are radacini reale deci graficul nu taie Ox

G_f Oy se calculeaza f(0)=c TC(0,c)

Varful parabolei V(

Exemplu: f(x x²+6x+5 ; a=1 deci parabola e convexa

G_f Ox x²+6x+5=0 Tx₁=-1 ,x₂=­­-5 T A(-1,0)si B(-5,0)

G_f Oy f(0)=5T C(0,5)

V(-3,-4)

Relatiile lui Viette

ax²+bx+c=0 S=x₁+x₂=

P=x₁ x₂=

Obs:

Totdeauna cand am o relatie intre radacini scriu relatiile lui Viette si folosesc acea relatie.

Exemplu:Fie ec. 3x² m-3)x+m+5=0 sa se determine m a.i. =

Sol: S= P= =S²-2P= T

= T = T 24=m²-6m+9-6m-30 T m²-12m-45=0 T m₁=-3 ,m₂=15

Formarea ecuatiei de gradul doi cand cunosc radacinile

Ecuata degradul doi cu radacini x₁,x₂ este x²-Sx+P=0 ,unde S=x₁+x₂ ,P=x₁ x₂

Exemplu :daca x₁=5,x₂=-3 TS=2, P=-15 Tec este :x²-2x-15=0

Descompunerea trinomului ax²+bx+c

ax²+bx+c=a(x-x₁)(x-x₂) unde x₁ ,x₂ sunt radacinile ecuatiei ax²+bx+c=0

Forma canonica a functiei de gradul II

Semnele radacinilor ecuatiei de gradul II

Cazul 1)S>0 si P>0 Tx₁>0 si x₂>0

Cazul 2) S<0 si P>0 Tx₁<0 si x₂<0

Cazul 3) P<0 nu conteaza semnul sumeiTx₁<0 si x₂>0

Exemplu: Fie ecuatia (m-2) 4^x+(2m-3)2^x+1+5m-6=0 A=/ec. Are o singura radacina reala}.

Sol: nota 2^x=y totdeauna cand faci o notatie ai grija noua variabila unde ia valori in acest caz 2^x ia valori positive Ty>0.

ecuatia devine (m-2) y² +(2m-3)2y +5m-6=0 unde y>0

cazul 1)=0 T4(2m-3)-4(m-2)(5m-6)=0 T 4m²-12m+9-5m²+16m-12=0T

-m²+4m-3=0T m=1,m=3

a) daca m=1 ecuatia devine –y²-2y-1=0 Ty=-1 T2^x=-1 imposibil

b) daca m=3 ecuatia devine y²+6y+9=0 Ty=-3 T2^x=-3 imposibil

cazul 2) >0 si y₁>0,y₂<0T 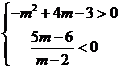TmI (,2)= (,2)

TmI(,2)

Observatie cand faci o notatie si nu e evident unde ia valori noua variabila notez f(x)=y si ii fac imaginea functiei f(x) .expl: notez =f(x) f’(x)= ln2 2x

TyI

Compararea radacinilor ecuatiei de gradul II cu o constanta

Cazul 1)x₁>a si x₂>a T x₁-a>0

x₂-a>0 adunand relatiile obtinem x₁+x₂-2a>0 TS-2a>0

inmultind relatiile obtinem( x₁-a)(x₂-a)>0T

x₁x₂-ax₁-ax₂+a²>0T P-aS+a²>0

Cazul 2) x₁<a si x₂<a T x₁-a<0

x₂-a<0 adunand relatiile obtinem x₁+x₂-2a<0 TS-2a<0

inmultind relatiile obtinem( x₁-a)(x₂-a)>0T

x₁x₂-ax₁-ax₂+a²>0T P-aS+a²>0

Cazul 2) x₁<a si x₂>a T x₁-a<0

x₂-a>0 nu se poate face suma

inmultind relatiile obtinem( x₁-a)(x₂-a)< 0T

x₁x₂-ax₁-ax₂+a²<0T P-aS+a²<0

Semnul functiei de gradul II

Cazul 1) D<0 functia are peste tot semnul lui a

Daca a>0 T

Daca a<0T

Cazul 2) D=0 functia in radacina e 0 in rest are semnul lui a

Daca a>0 T

Daca a<0T

Cazul 2) D>0 functia are intre radacini semnul contrar lui a si in afara semnul luia

Daca a>0 T

Daca a<0T

Aplicatie : Sa se det . parametrul a astfel incat (m-1)x²+mx+m+1>0 oricare ar fi x IR

Sol : cerinta revine la conditia ca expresia sa aiba peste tot semnul + adica

Adica pentru (m-1)x²+mx+m+1 trebuie sa avem D<0 si a>0

Tm²-4(m²-1)<0 si m-1>0T4-3m² <0 si m>1 T mI , ) (,+ (1,+ TmI(,+

In general daca cere ax²+bx+c>0 xIR punem conditia D<0 si a>0

daca cere ax²+bx+c0 xIR punem conditia D0 si a>0

daca cere ax²+bx+c<0 xIR punem conditia D<0 si a<0

daca cere ax²+bx+c0 xIR punem conditia D0 si a<0

Daca insa cere ca o expresie de gradul II sa aiba semn constant pe un interval sunt doua cazuri posibile : sau are semn ct pe toata axa numerelor reale sau are radacini in afara acelui interval exemplu: ax²+bx+c>0 xI

caz

Adica D<0 si a>0

Caz 2)

Adica D0 ,a>0 si x₁<0 ,x₂<0 T D0 ,a>0 S<0 ,P>0

Se rezova fiecare caz in parte iar la sfarsit solutiile cazurilor se reunesc.

Exemplu: sa se determine mIR astfel incat

(m+1)+2(m-3 +m>0 xIR

Solutie: not =y pentru ca am facut o notatie trebuie sa vadem y unde ia valori yI T conditia devine (m+1)y²+2(m-3)y+m>0 yI deci avem doua cazuri 1) sau avem semnul + pe toata axa nr. adica

Adica D<0 si a>0

T4(m-3)²-4m(m+1)<0 si m+1>0 T m2-6m+9-m²-m<0 si m>-1 T9-7m<0 si m>-1 TmI(,+ TmI(,+ ) not S₁=(,+

Cazul 2)ecuatia are doua radacini reale mai mici decat 1 astfel incat pe intervalul (1,+ ) sa aiba numai semnul +

Aceasta revine la conditiile D0 , a>0 y₁<1 ,y ₂<1

D0T mI ,] a>0T mI y₁<1 ,y₂<1T y₁-1<0 ,y₂-1<0

adunand obtinem S-2<0 T T T T TmI

inmultind relatiile obtinem (y₁-1)(y₂-1)>0 TP-S+1>0 T T

T TmI (,+

S₂= (- ,] (,+ )] =(,]

Solute finala este S₁ S₂=(,

Conditia ca doua ecuatii de gradul II sa aiba cel putin o radacina comuna

Notam cu a radacina lor comuna fiind radacina verifica ambele ecuatii si facem un sistem din cele doua ecuatii:

Exemplu: sa se determine m astfel incat urmatoarele doua ecuatii sa aiba cel putin o radacina comuna: 3x²+mx-22=0 si x²-(m+4)x+14=0

Fie a rad comuna T a verifica ambele ec. T

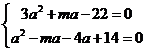adunnand obtinem 4a²-4a-8=0Ta₁=-1,a₂=2 daca a=-1Tm=-19

Daca a=2Tm=5

Conditia ca doua ecuatii de gradul II sa aiba ambele radacini commune

Trabuie ca cele doua ecuatii sa aiba coeficientii proportionali

Adica ax²+bx+c=0 si dx²+ex+f=0 au aceleasi radacini daca