GEOMETRIA LINIARĂ ÎN SPAŢIU

În acest capitol vor fi studiate varietatile liniare ale spatiului punctual euclidian ,= (E₃, V j ) pornind de la diferite moduri de precizare geometrica a lor. Varietatile liniare de dimensiune unu respectiv doi din spatiul E sunt subspatii afine proprii în spatiul afin , adica dreptele si respectiv planele afine.

Un subspatiu afin poate fi determinat fie de o submultime de puncte ale sale, fie de un punct al sau si de subspatiul director. Vom porni de la aceste conditii geometrice si vom caracteriza algebric dreptele si planele spatiului E raportându-ne la un reper cartezian ortonormat R (O; , , ).

Luând în considerare structura euclidiana a spatiului vectorial director V , vom aborda aspectele legate de unghiuri si distante.

§1. Planul în spatiu

În spatiul geometriei euclidiene E₃, un plan este în mod unic determinat de urmatoarele conditii:

1) trei puncte necoliniare

2) un punct si doua drepte neparalele

3) un punct si o dreapta perpendiculara pe plan.

1.1. Planul prin trei puncte

Fie M₀, M₁, M₂ E₃ trei puncte necoliniare (afin independente). Subspatiul afin p E₃ generat de punctele M₀, M₁, M₂ are ca spatiu vectorial director un subspatiu de dimensiune doi în spatiul vectorial V

dat de

V

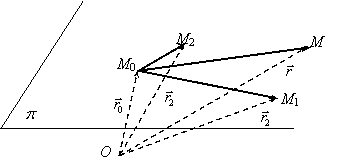
Un punct M p daca si numai daca V

fig.1.

Daca notam cu = , = , i = 0, 1, 2 vectori de pozitie ai punctelor M si respectiv M₀, M₁, M₂ în reperul cartezian R (O; , , ), (Oxyz) atunci multimea punctelor planului p va fi caracterizat de relatia vectoriala

, l m R  (1.1)

numita ecuatia vectoriala a planului prin trei puncte.

Daca (x, y, z), (x_i, y_i, z_i) R³, i = 0, 1, 2 sunt coordonatele punctelor M si respectiv M_i, i = 0, 1, 2 atunci ecuatia vectoriala (1.1) scrisa în reperul cartezian Oxyz este echivalenta cu ecuatiile

(1.2)

numite ecuatiile carteziene parametrice ale planului prin trei puncte.

Relatia = l+ m reprezinta conditia de coplanaritate a vectorilor , , echivalenta cu anularea produsului mixt, adica

(, , ) = 0 sau (,,) (1.3)

În coordonate carteziene ecuatia (1.3) se scrie sub forma

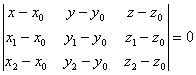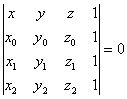sau (1.4)

numita ecuatie carteziana a planului prin trei puncte.

În particular, punctele A (a, 0, 0), B (0, b, 0), C (0, 0, c) situate pe axele de coordonate ale reperului Oxyz determina un plan p, iar coordonatele punctelor sale satisfac ecuatia

, sau dupa dezvoltare

(1.5)

numita ecuatia prin taieturi a planului p

Remarca. Conditia necesara si suficienta pentru ca patru puncte M_i(x_i,y_i, z_i), sa fie situate 242j91c într-un plan este

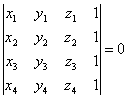(1.6)

1.2. Planul printr-un punct, paralel cu doua directii date

Fie punctul M₀ E₃ si dreptele distincte d₁, d₂ E . Consideram în punctul M₀ reprezentantii vectorilor (l₁, m₁, n₁) , (l₂, m₂, n₂) paraleli dreptelor d₁ respectiv d₂ (fig.2)

Vectorii si , liniar independenti genereaza subspatiul vectorial

V

fig.2

Punctul M₀ E₃ si subspatiul vectorial V determina subspatiul afin bidimensional p E₃. Un punct M p daca si numai daca V , adica vectorii , si sunt coplanari.

Utilizând vectorii de pozitie si corespunzatori punctelor M si respectiv M₀, relatia de coplanaritate se scrie sub forma

(1.7)

numita ecuatia vectoriala a planului printr-un punct, paralel cu doua directii.

Proiectând ecuatia (1.7) pe axele sistemului cartezian de coordonate Oxyz   obtinem:

numite ecuatiile carteziene sub forma parametrica ale planului printr-un punct, paralel cu doua directii.

Relatia de coplanaritate a vectorilor , si este caracterizata de anularea produsului mixt al celor trei vectori, adica (, ,) = 0. Obtinem astfel ecuatia

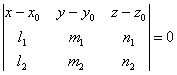(1.9)

numita ecuatia carteziana a planului printr-un punct, paralel cu doua directii.

Remarca. În particular, ecuatia (1.9) poate fi adaptata si pentru alte situatii cunoscute din geometria elementara, în care un plan este perfect determinat. Anume: planul determinat de o dreapta si un punct nesituat pe dreapta, planul determinat de doua drepte concurente si respectiv planul determinat de doua drepte paralele.

1.3. Planul printr-un punct, perpendicular pe o dreapta

Primele doua cazuri de determinare a unui plan sunt specifice unui spatiu afin, planul fiind gândit ca multimea suport a unui subspatiu afin de dimensiunea doi al spatiului afin E . Punând în valoare proprietatile oferite de structura euclidiana a spatiului vectorial V , putem caracteriza algebric punctele unui plan printr-un punct si care sa fie perpendicular pe o directie data.

Se stie din geometria elementara ca exista un singur plan si numai unul care trece printr-un punct si este perpendicular pe o dreapta data. Din punct de vedere algebric acest fapt se exprima în felul urmator: daca V este un subspatiu vectorial de dimensiune doi în spatiul vectorial euclidian al vectorilor liberi V atunci exista un unic complement ortogonal V , subspatiu de dimensiune unu, care permite scrierea în suma directa a spatiului vectorial al vectorilor liberi, sub forma V V V

Deci, determinarea planului afin p printr-un punct având ca spatiu vectorial director pe V este echivalenta cu determinarea planului printr-un punct având directia normalei paralela cu subspatiul V ortogonal subspatiului V

Un vector cu directie perpendiculara pe un plan va fi numit vectorul normal al planului sau pe scurt normala planului.

Fie un punct M₀ (x_o, y₀, z₀) E₃ si vectorul nenul (A, B, C) V în spatiul punctual euclidian E dotat cu reperul cartezian ortonormat R (O; , , ), (fig.3).

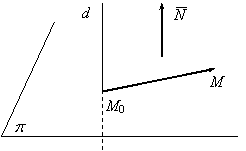
fig.3

Un punct M(x, y, z) este situat în planul p, planul prin punctul M₀ perpendicular pe dreapta   , daca si numai daca vectorul este ortogonal pe vectorul , adica = 0. Folosind expresia analitica a produsului scalar obtinem:

A(x - x₀) + B(y - y₀) + C(z - z₀) (1.10)

numita ecuatia planului printr-un punct si de normala data.

Prelucrând membrul stâng al ecuatiei (1.10) si notând cu D = - (Ax₀ + By₀ + Cz₀) obtinem:

Ax + By + Cz + D (1.11)

numita ecuatia carteziana generala a unui plan.

Observatii:

. Orice plan p E₃ este caracterizat într-un reper cartezian Oxyz de o ecuatie polinomiala de gradul I în nedeterminatele x, y, z si reciproc.

. În ecuatia (1.11) coeficientii nedeterminatelor reprezinta coordonatele vectorului normal la plan. În consecinta, doua plane ale caror ecuatii difera prin termenul liber sunt plane paralele, deci ecuatia

Ax + By + Cz = l , l R (1.12)

reprezinta familia planelor paralele din spatiu de normala data (A, B, C). Pentru l = 0 ecuatia (1.12) reprezinta ecuatia unui plan prin origine.

. Ecuatiile planelor de coordonate. Aceste plane contin originea, deci l = 0 si au ca normale vectorii reperului R (O; , , ), = (1,0,0), = (0,1,0), = (0,0,1). Obtinem:

z - ecuatia planului xOy

y - ecuatia planului xOz

x - ecuatia planului yOz

. Ecuatia normala a unui plan. Sa consideram planul p E₃ si punctul M₀ proiectia originii reperului R (O; , , ) pe planul p. Daca notam cu p distanta de la origine la planul p, cu a b g unghiurile pe care le face vectorul cu axele de coordonate atunci putem scrie:

= || = p (cosa + cosb + cosg

|||| = 1 cos²a cos²b cos²g

Un punct M (x, y, z) este situat în planul p daca si numai daca vectorii = p cosa + p cosb + p cosg si = - = = (x - p cosa) + (y - p cosb) + (z - p cosg) sunt ortogonali, adica = 0. În coordonate conditia de ortogonalitate este echivalenta cu:

x cosa + y cosb + z cosg - p = 0 (1.13)

numita ecuatia normala a planului sau ecuatia planului sub forma lui Hess.

În ecuatia (1.13) p R reprezinta distanta originii la planul p iar cantitatiile cosa, cosb cosg cu proprietatea cos²a cos²b cos²g = 1 reprezinta coordonatele versorului al directiei normale la planul p si vor fi numite cosinusurile directoare ale directiei .

Daca consideram planul p dat prin ecuatia generala Ax + By + Cz +D = 0, având normala = (A, B, C) si împartim ecuatia prin obtinem:

(1.14)

numita ecuatia normalizata a planului p Alegem semnul sau dupa cum D este negativ sau pozitiv, întrucât comparând ecuatia (1.14) cu ecuatia (1.13) avem , si termenul liber , în care p > 0, reprezinta o distanta.

1.4. Pozitia relativa a doua plane

Studiul pozitiilor geometrice a doua plane p p E₃:

plane ce se interesecteaza dupa o dreapta

plane paralele (strict)

plane confundate,

se reduce la studiul multimii solutiilor sistemului format cu ecuatiile celor doua plane.

Sa consideram în reperul cartezian ortonormat R (O; , , ) planele (p ): A₁x + B₁y + C₁z + D₁ = 0 si (p ): A₂x + B₂y + C₂z + D₂ = 0.

Daca notam cu matricea sistemului

(1.15)

avem urmatoarele cazuri:

- rang M = 2 sistemul (S ) este compatibil simplu nedeterminat.

Multimea solutiilor sistemului caracterizeaza locul geometric al punctelor comune celor doua plane, adica dreapta de intersectie a celor doua plane d = p p

- rang M = 1 si D_c = 0 - sistemul (S ) este compatibil dublu nedeterminat, adica cele doua plane coincid, p p

- rang M = 1 si D_c 0 - sistemul (S ) este incompatibil. Cele doua plane nu au nici un punct comun, p p

1.5. Pozitia relativa a trei plane

În spatiul punctual euclidian dotat cu reperul cartezian

R (O; , , ) consideram planele:

p ): A₁x + B₁y + C₁z + D₁ = 0

(S ) (p ): A₂x + B₂y + C₂z + D₂ = 0

p ): A₃x + B₃y + C₃z + D₃ = 0

Notam cu

,

matricea sistemului format cu ecuatiile celor trei planuri.

Avem urmatoarele cazuri:

a) rang M = 3 sistemul (S ) este compatibil determinat. Solutia sistemului reprezinta coordonatele punctului comun celor trei plane. Vom spune ca cele trei plane sunt concurente (snop de plane).

b) rang M = 2 si D_c sistemul (S ) este compatibil simplu nedeterminat. Multimea solutiilor reprezinta coordonatele punctelor situate pe o dreapta comuna celor trei plane. Spunem ca cele trei plane formeaza un fascicul de plane.

Conditiile rang M = 2 si D_c = 0 sunt echivalente cu faptul ca o ecuatie a sistemului (S ) este o combinatie liniara a celorlalte. Daca planele (p ) si (p ) determina o dreapta (d) atunci orice plan prin dreapta de intersectie este reprezentat analitic ca o combinatie a ecuatiilor celor doua plane. Ecuatia fasciculului de plane prin dreapta de intersectie a planelor p si p , numita axa fasciculului, este data de

l(A x + B₁y + C₁z + D₁) + m(A₂x + B₂y + C₂z + D₂) = 0 (1.16)

l m R, l m

Ecuatia A x + B₁y + C₁z + D₁ + a(A₂x + B₂y + C₂z + D₂) = 0, a R

reprezinta ecuatia fasciculului prin dreapta (d) din care lipseste planul p

În particular, axa Ox gândita ca intersectia planelor xOy si xOz,   determina fasciculul planelor prin Oz caracterizat de

ly mz (1.17)

c) rang M = 2 si D_c sistemul (S ) este incompatibil. Doua plane se intersecteaza dupa o dreapta, al treilea plan fiind paralel cu dreapta de intersectie a primelor doua plane ( planele formeaza o prisma)

d) rang M = 1 si = = 0 sistemul (S ) este compatibil dublu nedeterminat. Cele trei plane sunt confundate.

e) rang M = 1 si sistemul (S ) este incompatibil. Planele sunt paralele (strict sau doua pot fi confundate).

§2. Dreapta în spatiu

Fie R (O; , , ), un reper cartezian ortonormat în spatiul punctual euclidian E = (E₃, V j). Oricarui punct M E îi putem asocia vectorul de pozitie , unde terna (x, y, z) R , coordonatele vectorului în baza vor fi numite coordonatele punctului M.

În spatiul geometric E₃, o dreapta este unic determinata de urmatoarele conditii:

- un punct si de o directie data

- doua puncte distincte

- intersectia a doua plane

2.1. Dreapta determinata de un punct si o directie

Fie un punct M₀ E si vectorul nenul V . Vectorul nenul genereaza subspatiul vectorial unidimensional V

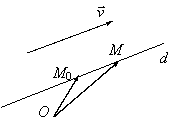
În aceste conditii subspatiul afin ce contine punctul M₀ si care admite pe V ₁ ca spatiu director ,va avea drept multime suport dreapta (d) ale carei puncte sunt date de

fig. 1

Conditia V are loc daca si numai daca l R asa încât = l . Scriind = obtinem

l R (2.1)

numita ecuatia vectoriala a dreptei (d) prin punctul M₀ având directia data de vectorul .

Daca proiectam relatia (2.1) pe axele reperului cartezian R(O,,,) obtinem:

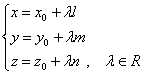(2.2)

numite ecuatiile parametrice ale dreptei d prin punctul M₀(x₀, y₀, z₀) având directia data de vectorul .

Vectorul = (l, m, n) V va fi numit vectorul director al dreptei (d) iar coordonatele l, m, n R vor fi numite parametrii directori ai dreptei (d).

Daca vectorul director este versorul , care formeaza unghiurile

a b g cu axele de coordonate Ox, Oy, Oz, atunci parametrii directori:

cosa, cosb, cosg, coordonatele versorului , se vor numi cosinusurile directoare ale dreptei (d).

Cosinusurile directoare ale unei directii în spatiu satisfac relatia

cos²a cos²b cos²g

Observatie: ecuatiile (2.1) sau forma echivalenta (2.2) guverneaza miscarea rectilinie si uniforma a unui punct material.

Eliminând parametrul l din ecuatiile (2.2) se obtin ecuatiile:

(2.3)

numite ecuatiile carteziene canonice (sub forma de rapoarte) ale dreptei d prin punctul M₀(x₀, y₀, z₀) si cu directia data de vectorul = (l, m, n)

Observatie. Ecuatiile canonice se scriu si când unul sau doi parametri directori sunt nuli, convenind în acest caz ca numaratorul corespunzator este nul si ca ecuatiile sunt date efectiv de egalarea produsului mezilor cu produsul extremilor în proportiile formate.

2.2. Dreapta determinata de doua puncte distincte

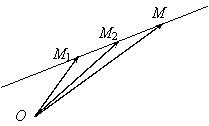
Fie M₁, M₂ E₃ doua puncte distincte. Subspatiul afin generat de aceste puncte va avea ca spatiu vectorial director subspatiul unidimensional V V dat de

V

fig. 2

Cu alte cuvinte un punct M E apartine multimii suport a subspatiului afin generat de punctele M₁ si M₂, adica M este situat pe dreapta prin cele doua puncte, daca si numai daca vectorii si sunt coliniari. Astfel, multimea punctelor dreptei prin M₁ si M₂ va fi caracterizata de relatia vectoriala

l R

sau

(2.4)

numita   ecuatia vectoriala a dreptei prin doua puncte.

În reperul cartezian R (O; , , ) , considerând M(x, y, z) , M₁(x₁, y₁, z₁) si M₂(x₂, y₂, z₂), vom obtine:

(2.5)

numite ecuatiile parametrice ale dreptei prin doua puncte.

Observatie: Pentru l (0, 1) ecuatiile (2.5) ne procura multimea punctelor de pe dreapta (d) cuprinse între punctele M₁ si M₂, iar pentru l R \ [0, 1] obtinem punctele dreptei (d), puncte exterioare segmentului M₁M₂. Pentru obtinem coordonatele mijloacelor segmentului M₁M₂.

Eliminarea parametrului l R în ecuatiile (2.5) sau impunând proportionalitatea coordonatelor a doi vectori coliniari, obtinem

(2.6)

numite ecuatiile carteziene sub forma canonica ale unei drepte prin doua puncte.

2.3. Dreapta ca intersectie a doua plane

Se stie din geometria elementara ca doua plane neparalele se intersecteaza dupa o dreapta (d). În paragraful precedent aceasta situatie geometrica este caracterizata analitic de un sistem de ecuatii liniare compatibil nedeterminat, format cu ecuatiile celor doua plane. Astfel, ecuatiile sistemului

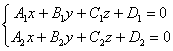(2.7)

vor fi numite ecuatiile dreptei (d) data de intersectia a doua plane.

O solutie (x₀, y₀, z₀) a sistemului (2.7) va caracteriza un punct al dreptei (d) iar vectorul , unde si sunt normalele celor doua plane ce determina dreapta (d).

Observatie :

Ecuatiile carteziene (2.3) si (2.6) ale unei drepte în spatiu pot fi interpretate ca un sistem de doua ecuatii liniare, adica dreapta (d) gândita ca intersectia a doua plane.

2.4. Pozitia relativa a doua drepte

Fie dreptele (d₁) si (d₂) date de ecuatiile

(d₁)

(d₂)

Consideram vectorii = (l₁, m₁, n₁), = (l₂, m₂, n₂) - vectori directori ai dreptelor (d₁) respectiv (d₂) si vectorul , unde M₁(x₁, y₁, z₁) d₁ respectiv M₂(x₂, y₂, z₂) d₂.

Avem cazurile:

a) daca (, , ) 0 - dreptele (d₁) si (d₂) sunt necoplanare sau drepte oarecare în spatiu (strâmb asezate în spatiu)

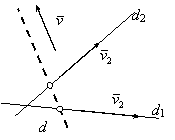
În acest caz exista o directie comuna normala unica pe cele doua drepte, data de =× si deci o unica dreapta care se sprijina pe cele doua drepte având directia (fig. 3), numita perpendiculara comuna a dreptelor (d₁) si (d₂).

fig. 3

Perpendiculara comuna (d) este data de intersectia planelor p si p p - planul prin dreapta (d₁) paralel cu si p - planul prin (d₂) paralel cu . Ecuatiile perpendicularei comune sunt:

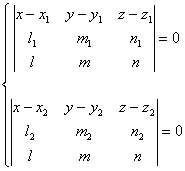(2.8)

unde (l, m, n) = = ×

b) daca (, , ) = 0 - dreptele (d₁) si (d₂) sunt coplanare

b₁) l - drepte concurente

b₂) = l - drepte paralele (strict)

b₃) = l si = m - drepte confundate

§3. Unghiuri si distante

Fie (d) o dreapta în spatiul punctual euclidian E₃. Pe dreapta (d) se pot stabili doua sensuri de parcurs. O dreapta (d) împreuna cu o alegere a unui sens de parcurs se numeste dreapta orientata.

Daca este vectorul director al dreptei (d), atunci vom alege sensul de parcurs pe dreapta sensul lui (sens pozitiv).

Fie planul p E₃ având vectorul normal . Planul are doua fete iar alegerea unui sens pe dreapta normala este echivalenta cu alegerea unei fete a planului. Un plan p împreuna cu o alegere a sensului pe normala se numeste   plan orientat. Vom alege sensul pe normala sensul dat de vectorul

3.1. Unghiul a doua drepte în spatiu

Fie dreptele (d₁) si (d₂) orientate de vectori directori = (l₁, m₁, n₁) si respectiv = (l₂, m₂, n₂).

Prin unghiul dreptelor (d₁) si (d₂) vom întelege unghiul j p], unghiul dintre vectorii si , dat de

cosj = (3.1)

În particular avem:

d₁ d = 0 l₁l₂+m₁m₂+n₁n₂ = 0

× =

3.2. Unghiul a doua plane

Fie planele neparalele p si p , date de

p ) A₁x + B₁y + C₁z + D₁ = 0

p A₂x + B₂y + C₂z + D₂ = 0

În geometria elementara unghiul a doua plane neparalele este definit ca fiind unghiul diedru al celor doua plane. Acest unghi este congruent sau suplementar cu unghiul vectorilor si , vectorii normali planelor p respectiv p

Acceptam ca unghiul diedru determinat de planele orientate p si p sa fie masurat prin unghiul dintre ₁ si ₂ . Acest unghi este dat de

cosj = 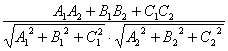(3.2)

În particular p p A₁A₂+B₁B₂+C₁C₂ = 0

3.3. Unghiul dintre o dreapta si un plan

Unghiul dintre o dreapta si un plan este definit în geometria elementara ca fiind unghiul dintre dreapta si proiectia ortogonala a acesteia pe plan.

Fie dreapta (d) orientata de vectorul director = (l, m, n) si palnul p orientat de normala (fig. 5)

fig. 5

Unghiul j ] dintre dreapta (d) si planul p este legat de unghiul q, unghiul vectorilor si , prin relatiile q j ,deci .Astfel obtinem :

= (3.3)

În particular:

d p = 0 lA + mB + nC = 0,

d p = .

3.4 Distanta de la un punct la o dreapta

Reamintim ca distanta dintre doua submultimi S₁ si S₂ într-un spatiu metric este data de d ( S₁, S₂) = inf

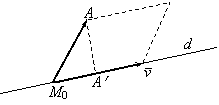
În spatiul punctual euclidian E dotat cu metrica euclidiana distanta dintre doua submultimi se reduce la distanta dintre doua puncte. Astfel, distanta de la un punct la o dreapta este data de distanta dintre punct si proiectia ortogonala a acestuia pe dreapta (fig. 6)

fig. 6

Fie dreapta (d) prin punctul M₀, orientata prin vectorul director , punctul A exterior dreptei si A proiectia acestuia pe dreapta (d). Determinând punctul A , ca intersectia dreptei (d) cu planul prin A ortogonal dreptei, obtinem d (A, d) = d (A, A Altfel, construind paralelogramul determinat de vectorii si , obtinem

d (A, d) = d (A, A (3.4)

3.5. Distanta de la un punct la un plan

Distanta de la un punct M₀ la un plan (p Ax + By + Cz + D = 0 este data de distanta dintre punctul M₀(x₀, y₀, z₀) si punctul M (x , y , z ), proiectia ortogonala a acestuiape planul p

Determinam coordonatele (x , y , z ) ale punctului M , rezolvând sistemul format de ecuatia planului si ecuatiile dreptei prin punctul M₀ ortogonala pe plan, adica:

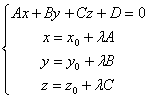(3.5)

Parametrul pe dreapta corespunzator punctului M , notat cu l , este dat de

l = - si obtinem

d (M₀,M

= =

iar distanta de la punctul M₀ la planul p este data de

d (M₀, p (3.6)

Observatie: Distanta de la un punct M₀ la un plan p se obtine luând modulul expresiei obtinute prin înlocuirea coordonatelor punctului dat în membrul stâng al ecuatiei normalizate a planului.

3.6. Distanta dintre doua drepte oarecare în spatiu

Fie dreptele oarecare în spatiu

(d₁)

(d₂)

Fie (d) perpendiculara comuna a dreptelor (d₁) si (d₂) iar P₁ respectiv P₂ punctele de contact ale acesteia cu (d₁) respectiv (d₂).

Construim paralelipipedul determinat de vectorii = = (x₂-x₁, y₂-y₁, z₂-z₁), = (l₁, m₁, n₁) si = (l₂, m₂, n₂). (fig. 7)

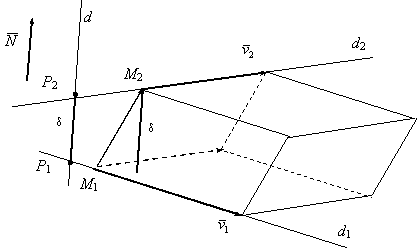
fig. 7

Distanta dintre dreptele (d₁) si (d₂) este data de distanta dintre punctele de contact ale perpendicularei comune cu cele doua drepte, distanta ce reprezinta înaltimea paralelipipedului construit. Astfel, obtinem

d (d₁, d₂) = d (P₁, P₂) = (3.7)

§4. Probleme propuse

1. Se dau A ( 3, 1, 0), B ( 2, 1, -1), C ( 3, 2, 1). Sa se scrie ecuatia unui plan:

a)      care trece prin A, B, C;

b)      care trece prin B si este paralel cu xOy;

c)      care trece prin C si contine axa Oz;

d)      care trece prin B, C si este paralel cu Oy.

. Sa se scrie ecuatia planului care trece prin punctul M ( 2, 0, 1) si este perpendicular pe planele (P₁) : x + y + z = 0 si (P₂): x - 2y + 3z = 1.

. Sa se scrie ecuatia unui plan paralel cu planul (P) x + y + z = 3 si care trece prin mijlocul segmentului determinat de punctele M₁ ( 1, 3, 2) si M ( -1, 3 , 4).

. Sa se determine ecuatia planului care trece prin M ( -1, 1, 0) si taie pe axele de coordonate segmente proportionale cu numerele 2, 3, 4.

. Fie planul .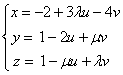

Sa se gaseasca l si m astfel încât planul sa fie ortogonal pe vectorul ( 1, 7, 11). Sa se scrie ecuatia generala a planului.

. Fie triunghiul A, B, C cu A ( 0, 2, 0), B ( 3, 2, 1), C ( 0, 1, 2). Sa se scrie ecuatiile:

a)     înaltimii din A;

b)    medianei din B;

c)     mediatoarei laturii AB.

. Sa se scrie ecuatiile dreptei care trece prin M (1,-1,1) si este paralela cu dreapta de intersectie a planelor (P₁) x + y = 3 si (P₂) x - z = 1.

. Un mobil M se deplaseaza în spatiu pe traiectoria data de

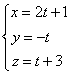
Sa se determine momentul t la care mobilul se afla în planul x + y + z = 0 si sa se scrie ecuatiile carteziene ale acestei traiectorii.

. Gasiti a b R astfel încât dreapta sa fie continuta în planul x - z = 0 si sa treaca prin M ( 1, 1, 1).

. Sa se scrie ecuatia planului care trece prin M₀ ( 2, -1, 1) si este perpendicular pe dreapta definita de planele (P₁) : x + 2y + 2z + 2 = 0 si (P₂) : x - y + z + 1= 1.

. Sa se scrie ecuatia planului care trece prin mijlocul segmentului M ( 1, -1, 2), N ( 4, -3, 1), este paralel cu dreapta si perpendicular pe planul x - 2y - z -1 = 0.

. Sa se scrie ecuatiile dreptei continute în planul (P) x + 3y+ 2z -2 = 0, care se sprijina pe dreapta x = y = z si este paralela cu planul 4x - y - z - 3 = 0.

. Sa se scrie ecuatiile proiectiei dreptei pe planul 3x - 2y + z - 4 = 0.

. Sa se scrie ecuatia unui plan paralel cu planul (P) 3x + 5y + z = 0 care trece prin punctul M ( 2, 0 , 5).

. Sa se scrie planul care trece prin A ( 3, 1, -2) si care contine dreapta .

. Fie punctul M ( 2, 1, 0) si planul (P) 2x + 2y + z = 1. Sa se determine:

a)      proiectia lui M pe plan;

b)      simetricul lui M fata de plan;

c)      distanta de la M la (P).

. Fie dreapta (d) si planul (P) 2x - y + z = 0. Sa se determine proiectia dreptei (d) pe planul (P).

. Sa se scrie ecuatia unui plan care trece prin dreapta si care este perpendicular pe planul x + y + z = 0.

. Sa se scrie ecuatiile dreptei care trece prin A ( 3, 1, -1) si se sprijina pe dreptele

a)           si

b)          si x = -t, y = 2t + 1, z = 3t.

. Pe dreapta sa se gaseasca un punct egal departat de punctele A ( 3, 14, 4) si B ( 5, -13, -2).

. Sa se gaseasca unghiul dintre dreptele

si

. Calculati unghiul pe care îl face dreapta (d) : si planul 2x + 2y - z - 3 = 0.

. Sa se determine unghiul dintre planele x + y + 2z = 1, 2x - y + 2z = 3.

. Sa se scrie ecuatiile perpendicularei comune si sa se calculeze distanta dintre dreptele:

a)      (d₁): si (d₂):

b)      (d₁): si (d₂):

. Sa se arate ca dreptele (d₁): si (d₂): sunt oarecare în spatiu si sa se determine distanta dintre ele.

. Sa se determine a si b astfel încât planele:

p ): x + 2y + z = a

p ax

p ): x + by + z = 0,

a)      sa se intersecteze dupa o dreapta;

b)      sa se intersecteze într-un punct;

c)      sa formeze o prisma.

. Sa se determine simetrica dreptei (D): fata de planul xOy.

. Sa se determine simetricul planului 2x + y - 2z = 1 fata de planul x + y + z = 0.