INELE

Definitia inelului. Exemple

Definitie : Fie A o multime inzestrata cu doua operatii binare notate prin simbolurile + si si numite operatie de adunare respectiv de înmultire. Tripletul (A,+, ) se numeste inel daca satisface conditiile ( axiomele)

(i)   &nb 434g69e sp;   &nb 434g69e sp;   &nb 434g69e sp;   &nb 434g69e sp;  (A,+) este grup abelian (comutativ) ;

(ii)   &nb 434g69e sp;   &nb 434g69e sp;   &nb 434g69e sp;    (A, ) este semigrup ;

(iii)   &nb 434g69e sp;   &nb 434g69e sp;   &nb 434g69e sp;   Pentru orice a, b, c A ,

a (b + c) = ab + ac

(a + b) c = ac + bc ,

adica operatia de înmultire este distributiva, atât la stânga cât si la dreapta, fata de operatia de adunare.

Explicitând proprietatile 1, 2 si 3, (A, +, ) este inel daca:

(x + y) + z = x + (y + z) , () x, y, z A.

A a. i. 0 + x = x + 0 = x , (") x A

") x A , -x A a.i. x + (- x ) = (- x) + x = 0

x(yz) = (xy)z , () x,y,z A

Observam ca A , deoarece cel putin elementul neutru fata de operatia de adunare trebuie sa apartina lui A, adica notând acest element prin 0 , neaparat 0A . Elementul 0 se numeste elementul zero al inelului, prin analogie cu numarul întreg zero, care joaca rolul de element neutru fata de operatia de adunare în Z.

Daca A nu contine alte elemente, diferite de elementul zero, atunci inelul (A,+, ) se numeste inel nul . Mai mult, se observa ca pentru orice multime formata dintr-un singur element exista o singura structura de inel, inelul nul.

Exemple de inele:

(Z,+, ), (Q,+, ), (R,+, ), (C,+, ) sunt inele comutative si unitare.

Mentionam ca multimea numerelor naturale , împreuna cu operatiile de adunare si înmultire , definite în modul cunoscut în aceasta multime , nu formeaza inel, întrucât (N, +) nu este grup.

(Z[i],+, ) numit inelul întregilor lui Gauss,

unde Z[i]=, iar operatiile + si sunt cele uzuale cu numere complexe. Se verifica usor ca (Z[i], +, ) este inel comutativ unitar.

(Zn ,+, ) este inel comutativ unitar, inelul claselor de resturi modulo n.

Exemple concrete de inele:

1. Presupunând cunoscuta constructia numerelor naturale N, precum si proprietatile operatiilor de adunare si înmultire cu numere naturale, putem construi inelul numerelor întregi. Pentru aceasta sa consideram produsul cartezian si definim în aceasta multime o relatie binara ≈ astfel

Relatia ≈ este o relatie în N x N, deci putem construi multimea cât  Z = N x N/_≈ , adica , unde

Definind în Z operatiile binare + si prin

se constata ca (Z, +, ) este un inel unitar si comutativ , având ca element zero clasa iar ca element unitate clasa . Pentru simplificarea scrierii se noteaza =1 si =1

Sa aratam ca inelul (Z, +, ) nu admite divizori ai lui zero nebanali. Pentru aceasta, fie si doua numere întregi pentru care ab = 0 , adica

deci,

de unde obtinem

Daca m = n sau p = q , atunci sau

Daca m > n ( > fiind relatia de ordine definita în modul cunoscut în N) , atunci exista l N , l , astfel încât m = n + l , deci

(n + 1)p + nq = (n + 1)q + np

adica

np + lp + nq = nq + lq + np

de unde , aplicând legile comutativitatii si simplificarii valabile pentru operatiile din N , primim p = q , prin urmare .

În cazul m < n se obtine b = 0 , iar în cazul p < q sau p > q se obtine a = 0 .

2. Sa notam prin M_n multimea tuturor matricilor patratice de ordin n (n N)

având elementele dintr-un inel (A,+, ) . Definind operatiile de adunare si înmultire a matricilor în modul cunoscut, adica

(i, j= 1,2, ,n)

tripletul (M_n, +, ) devine inel. Elementul zero al acestui inel este matricea care are toate elementele egale cu elementul 0 A . Daca inelul poseda element unitate, atunci si inelul (M_n, +, ) , poseda element unitate. De asemenea, se stie ca operatia de înmultire a matricilor este, în general, necomutativa , deci inelul (M_n, +, ), va fi necomutativ. În sfârsit, se constata ca (M_n, +, ) , admite divizori ai lui zero. Într-adevar, daca consideram de exemplu inelul matricilor cu elemente din Z, atunci

desi fiecare dintre matricile ce se înmultesc sunt diferite de matricea zero.

3. Fie (A, +, ) un inel si M o multime, M ≠ Ř . Sa notam prin A^M multimea tuturor functiilor de la M la A. Pentru fiecare f, g A^M sa definim suma si produsul acestor doua functii astfel:

(f + g) (x) = f(x) + g(x)

(f g) (x) = f(x) g(x)

Se observa imediat ca f + g si f g sunt functii de la M la A , adica f + g , f g A^M. Apoi se constata ca (A^M, +, ) formeaza un inel pentru care elementul zero este functia z : M A definita prin z(x) = 0 (x M) . Acest inel este cu element unitate daca (A, +, ) poseda element de unitate . Într-adevar , daca 1 A este elementul unitate în inelul (A, +, ) , atunci functia ε : M A, definita prin ε(x) = 1 va fi element unitate în inelul (A^M, +, ) . De asemenea , daca (A, +, ) este comutativ , atunci si inelul (A^M, +, ) va fi comutativ.

În sfârsit , se constata ca acest inel este cu divizori ai lui zero. Pentru a dovedi acest lucru sa consideram , de exemplu , în inelul (Z^Z, +, ) functiile f, g : Z Z definite prin

daca x ≤ 0

daca x >

în rest

Observam ca pentru orice x Z avem (fg) (x) = f(x) g(x) = 0 , adica fg = z , desi atât f cât si g sunt diferite de elementul zero al inelului (Z^Z, +,

1.2.   &nb 434g69e sp;   &nb 434g69e sp;   Proprietati de baza ale inelelor

Teorema 1.2.1. Pentru fiecare a A , a a = 0 .

Demonstratie. Pentru orice a A , a 0 = a(0 + 0) = a 0 + a 0 , deci simplificând în grupul aditiv (A, + ) prin a 0 , obtinem a 0 = 0 . Similar se demonstreaza ca 0 a = 0 .

Teorema 1.2.2. Pentru orice a, b, c A ,

a(b - c) = ab - ac ;

(a - b)c = ac - bc ,

adica operatia de înmultire este distributiva fata de operatia de scadere , atât la stânga cât si la dreapta .

Demonstratie. În grupul (A, +) operatia de scadere se defineste prin formula a - b = a + ( - b) , deci pentru orice a, b, c A , (b - c) + c = b , adica  a[(b - c) + c] = ab deci a(b - c) + ac = ab , de unde primim a(b - c) = ab - ac . A doua egalitate se demonstreaza similar .

Teorema 1.2.3. Pentru orice a, b A, ( - a)b = a(- b) = - ab si de asemenea ( - a)( - b) = ab .

Demonstratie. Daca a, b A , atunci ab + ( - a)b = [a + ( -a)]b = 0 b = 0 si la fel, ab + a( - b) = a[b + ( - b)] = 0 , deci ( - a)b = a( - b) = - ab .

Apoi , ( - a) ( - b) = - [a( - b)] = ab .

Inelul (A, +, ) se numeste inel cu element unitate (sau inel unitar) , daca satisface conditia :

(iv) Exista elementul 1 A , astfel încât pentru orice a A, a a = a.

Daca inelul (A, +, ) este unitar , atunci are sens sa vorbim despre elementele inversabile (simetrizabile) ale acestui inel. Anume, elementul a A se numeste inversabil daca exista a ^{- 1} A cu proprietatea aa ^{- 1} = a ^{- 1} a = 1 .

Exemple: Inelele (Z ,+ , ) , (Q , + , ) , (R ,+ , ) , (C , + , ) , (Z[i], + , ) sunt domenii de integritate . Daca A este un inel unitar , elementele lui simetrizabile in raport cu înmultirea se numesc elemente inversabile sau unitati ale inelului..

Inversul sau simetricul lui a ,daca exista , se noteaza cu a .

Teorema 1.2.4. Multimea elementelor inversabile ale inelului unitar (A, +, ) formeaza grup în raport cu operatia de înmultire indusa.

Demonstratie. Fie S = si sa aratam ca (S, ) satisface axiomele grupului :

Daca a, b S , atunci a ^{- 1} , b ^{- 1} A , astfel încât aa ^{- 1} = a ^{- 1} a = 1 si bb ^-1 = b ^{- 1} b = 1, deci

(ab) (b ^{- 1} a ^{- 1} ) = a(bb ^{- 1} )a ^{- 1} = a a ^{- 1} = aa ^{- 1} =1 ,

(b ^{- 1} a ^-1 )(ab) = b ^-1 (a ^-1 a)b = b ^-1 b = b ^-1 b = 1,

adica ab S .

Asociativitatea operatiei induse este evidenta , ea se transmite de la inelul (A, +,

Deoarece 1 1 = 1, obtinem 1 S si astfel acesta va juca rol de element neutru si pentru elementele din S.

În sfârsit , daca a S, atunci exista a ^-1 A astfel încât aa ^-1 = a ^-1 a = 1, deci întrucât proprietatea de "a fi simetric" este reciproca, obtinem ca a ^-1 S.

Inelul (A, +, ) se numeste comutativ daca satisface conditia:

(v) Pentru orice a, b A, ab = ba .

Fie (A, +, ) un inel. Elementul a A se numeste divizor al lui zero , daca exista b A, b 0 , astfel încât ab = ba = 0

Observam imediat ca , pentru orice inel (A, +, ) nenul , elementul 0 este în mod banal divizor al lui zero. Prezinta interes faptul daca un inel admite si divizori ai lui zero nebanali .

Un inel care nu admite divizori ai lui zero nebanali se va numi inel fara divizori ai lui zero.

Inelul (A, +, ) se numeste domeniu de integritate daca este comutativ , cu element unitate si fara divizori ai lui zero .

Exemplu: (1) (Z, +, ) este un domeniu de integritate deoarece

- este comutativ

-   &nb 434g69e sp;   &nb 434g69e sp; este unitar, - contine pe 1

-   &nb 434g69e sp;   &nb 434g69e sp; nu are divizori ai lui zero

(Z_n , +,

Teorema 1.2.5. Daca (A, +, ) este inel si a A nu este divizor al lui zero, atunci ax = ay sau xa = ya implica x = y. În particular, intr-un domeniu de integritate este valabila legea simplificarii .

Demonstratie. Daca ax = ay , atunci ax - ay = 0, deci a(x - y) = 0, prin urmare x - y = 0 si astfel x = y .

Teorema 1.2.6. Elementele inversabile dintr-un inel unitar nu sunt divizori ai lui zero .

Demonstratie. Sa presupunem ca elementul a A este inversabil, adica exista a ^-1 A cu proprietatea aa ^-1 = a ^-1 a = 1 . Daca a a ar fi divizor al lui zero , atunci exista b a , b 0 , astfel încât ab = 0, deci a ^-1 (ab) = (a ^-1 a)b = b = 0, ceea ce contrazice faptul ca b

Din aceasta teorie rezulta ca un inel unitar este nenul , deoarece contine cel putin elementele 0 si 1 , 1

1.3. Subinele

Definitie. Fie (A,+, ) un inel si SA, S . Considerând operatiile induse în S din A, tripletul (S,+,) se numeste subinel al inelului (A,+, ) daca la rândul sau formeaza inel.

Teorema 1.3.1. Daca (A,+, ) este inel si SA, S , atunci S va fi subinel daca si numai daca se satisfac conditiile:

(1)   &nb 434g69e sp;   &nb 434g69e sp; Pentru orice a, b S, a + b S (teorema de închidere a sumei);

(2)   &nb 434g69e sp;   &nb 434g69e sp; Pentru orice a S, -a S ;

(3)   &nb 434g69e sp;   &nb 434g69e sp; Pentru orice a, b S, a b S (conditia de închidere a produsului);

Demonstratie. Aceste conditii sunt evident necesare, deoarece coincid cu o parte dintre axiomele ce definesc inelul . Observam insa ca ele sunt si suficiente . Într-adevar conditia (1) ne asigura închiderea parte din axiomele ce definesc inelul operatiei de adunare in S, legile asociativitatii si comutativitatii pastrându-se evident si pentru operatia de adunare indusa, Conditia (2) ne asigura existenta opusului pentru fiecare element din S . Apoi, observam ca deoarece S , exista a S  astfel încât , -a S , deci prin conditia (1) a + (-a) = 0 S . Proprietatea de asociativitate a operatiei de înmultire si legile distributivitatii ale acesteia fata de adunare se transmit de la întregul inel A.

Teorema 1.3.2. Daca (A,+, ) este inel si SA, S , atunci (S,+, ) va fi subinel daca si numai daca satisface conditiile:

(1)   &nb 434g69e sp;   &nb 434g69e sp; Pentru orice b S , a - b S (conditia de închidere a operatiei de scadere)

Pentru orice a, b S, a b S  (conditia de închidere a produsului).

Demonstratie. Daca (S, +, ) este subinel, atunci din teorema (1.3.1.) rezulta ca pentru orice b S , -b S , deci pentru orice b S , a + (-b) = a - b S  si astfel este satisfacuta conditia (1) , iar conditia (2) coincide cu conditia (3) din teorema precedenta .

Invers, sa presupunem ca submultimea S satisface conditiile (1) si (2). Atunci, pentru orice a S , a - a = 0 S , deci pentru orice b S , 0 - b = - b S  si astfel pentru orice a b S , a -(- b) = a + b S . Prin urmare se satisfac conditiile teoremei, 1.3.1. , deci (S, +, este subinel al inelului (A, +,

Teorema 1.3.3. Daca (A, +, ) este inel si SA, S este o submultime finita a lui A, atunci (S, +, ) va fi subinel daca si numai daca satisface conditiile:

(1)   &nb 434g69e sp;  Pentru orice a, b S , a + b S ;

(2) Pentru orice a, b S, ab S .

Demonstratie. Conditiile sunt evident necesare. Sa aratam ca ele sunt si suficiente. Pentru aceasta observam ca este de ajuns sa demonstram ca este satisfacuta conditia (2) formulata în teorema 1.3.1. Fie S = si pentru a S sa notam a + S = . Se constata ca pentru orice a S, a + S = S, deci pentru orice a, b S ecuatia a + x = b are solutie în S. În particular, ecuatia a + x = a are solutie în S , deci exista x₀ S astfel încât x₀ + a = b. Prin urmare , pentru orice b S , b + 0 = ( x₀ + a ) + 0 = x₀ + ( a + 0 ) = x₀ + a = b, adica 0 joaca rol de element neutru pentru operatia de adunare din S. În sfârsit, din faptul ca pentru orice a S ecuatia a + x = 0 are solutie în S rezulta conditia de demonstrat.

Observam ca daca (A, +, ) este unitar si (S, +, ) este un subinel al acestui inel, atunci elementul 1 A nu apartine obligatoriu si lui S. Asa, de exemplu , (2Z, +, este un subinel al inelului (Z, +, pentru care 1 2Z.

Pentru fiecare inel (A, +, tripletele ( si însasi (A, +, sunt subinele banale ale acestui inel. Exista insa inele care admit subinele nebanale . Un astfel de inel, este, de exemplu (Z, +, ) care admite ca subinele toate tripletele (nZ, +, , oricare ar fi n N.

Teorema 1.3.4. Daca S i ), i I , sunt subinele ale inelului (A, +,

atunci este subinel al inelului (A, +,

Demonstratie. Observam ca ≠ Ř, deoarece cel putin . Apoi, (, +, este subgrup al grupului (A, +, ), deci va fi suficient sa aratam ca operatia de înmultire indusa pe este închisa . Pentru aceasta, observam ca daca a, b , atunci pentru fiecare i I ; a, b S_i , deci pentru fiecare i I; ab S_i , adica ab .

Se constata însa ca , în general, reuniunea unei familii de subinele nu este

subinel. Pentru a ne convinge de acest lucru sa consideram subinelele (2Z, +, ) si (3Z, +, ) ale inelului (Z, +, ) . Se stie ca operatia de adunare indusa pe submultimea 2Z 3Z nu este închisa , deci reuniunea acestor doua subinele nu va fi subinel al inelului (Z, +,

Cu toate acestea, este adevarat a urmatoarea afirmatie:

Teorema 1.3.5. Daca (Si, +, ), este o familie de subinele ale inelului (A, +, ) , atunci exista subinelul (S, +, ) al inelului cu proprietatile:

(1) Pentru fiecare i I ,S S_i ;

(2) Daca pentru fiecare i I subinel (S^', +, ) al inelului are proprietatea S^' S_i , atunci S^' S.

Subinelul (S, +, ) , astfel determinat, se numeste subinelul generat în inelul

(A, +, ) de familia de subinele S_i .

Demonstratie. Se considera multimea tuturor subinelelor (X, +, ) ale inelului (A, +, ) care poseda proprietatea ca pentru fiecare i I, X S_i . Aceasta multime este nevida , deoarece cel putin A poseda aceasta proprietate. Intersectia tuturor acestor subinele este un subinel care poseda proprietatile (1) si (2).

Teorema 1.3.6. Daca (A, +, ) este inel si M A, atunci exista subinelul (S, +, ) al inelului (A, +, ) cu proprietatile :

1.   &nb 434g69e sp;   &nb 434g69e sp;    S M;

2.   &nb 434g69e sp;   &nb 434g69e sp;    Daca (S^', +, ) este un subinel al inelului (A, +, ) cu proprietatea

S^' M, atunci S^' S .

Subinelul (S, +, ) astfel determinat, se numeste subinelul generat în inelul

(A, +, ) de submultimea M A . Evident, daca M = Ř, atunci subinelul generat de M coincide cu subinelul zero .

Deoarece teoremele precedente ne asigura numai existenta subinelului generat , e bine sa aratam si modul cum se poate obtine efectiv acest subinel.

Teorema 1.3.7. Subinelul generat în inelul (A, +, ) de submultimea M A,

M ≠ Ř , este format din toate sumele finite de forma , unde x_k M sau - x_k M (k = 1, 2, ., n) . În particular, subinelul generat de familia de subinele (S_j, + , ) i I , va fi format din toate sumele finite de forma , unde x_k

Demonstratie. Notând , se constata ca S M si ca diferenta si produsul a doua elemente din S sunt tot elemente din S. Deci (S, +, ), este un subinel al inelului (A, +, ) . Apoi , daca (S', +, ) este un

subinel al inelului (A, +, ) care contine pe M , atunci acesta (prin calitatea sa de subinel) va contine si elementele din S, deci S' S .

În sfârsit, observam ca oricare ar fi subinelele (S₁, +, ) si (S₂, +, ) ale inelului (A, +, ) , S₁ S₂ Inf . De asemenea, notând prin <S₁ S₂> subinelul generat de aceste subinele, prin (2.7), < S₁ S₂> Sup

Exemple:

Daca A este un inel, atunci A si sunt subinele, numite subinele improprii.

(Z, +, ) si (Q, +, ) sunt subinele ale inelului (R, +,

Z Q R sunt subinele unul în altul , cu adunarea si înmultirea numerelor .

Fie n N. Multimea H = nZ = este un subgrup al grupului aditiv (Z, +). Daca avem x, y H, atunci x = nk1, y = nk2, k1, k2 Z, deci xy = nk1k2 H, adica H este un subinel al lui Z. Deci, orice grup al grupului aditiv al lui Z este un subinel al inelului Z, deoarece orice subgrup al lui (Z, +) este de forma nZ , cu n N.

Reciproc, deoarece orice subinel al unui inel trebuie sa fie subgrup al grupului aditiv al inelului respectiv, rezulta ca orice subinel al lui Z este de forma H = nZ . Deci subinelele inelului Z coincid cu subgrupurile lui (Z, +), care sunt de forma nZ , n N .

Mai exact fiecare subinel este format din multipli întregi ai celui mai mic numar natural nenul sau zero ce apartine subinelului.

1.4.   &nb 434g69e sp;   &nb 434g69e sp;   Ideale

Definitie. Fie (A, +, ) un inel si IA , I . Consideram operatiile induse în I din A, tripletul (I, +, se numeste ideal al inelului (A, +, daca satisface conditiile:

(i) Pentru orice a , b I, a - b I ;

(ii) Pentru orice x A si orice , a I, xa I ;

(iii) Pentru orice x A si orice a I, ax I .

Din conditia (i) rezulta ca (I, +) este un subgrup al grupului aditiv (A, +) iar din conditia (ii) sau (iii) rezulta ca pentru orice a, b I avem ab I. Deci fiecare ideal al inelului (A, +, este, în particular, un subinel al acestui inel. Afirmatia inversa nu este, în general, adevarata . Într-adevar , de exemplu, (Z, +, ) este un subinel al inelului (Q, +, ) fara a fi ideal.

Daca sunt satisfacute numai conditiile (i) si (ii, atunci tripletul (I, +, se numeste ideal stâng al inelului (A, +, ) iar daca satisfac conditiile (i) si (iii) , atunci (I, +, ) se numeste ideal drept . Aceste notiuni sunt distincte, în sensul ca idealele stângi ale unui inel nu coincid obligatoriu cu idealele drepte. Asa de exemplu, daca în inelul matricilor patratice de ordin n,n > 1, cu elemente din Z, am considera multimea matricilor care au elementele de pe prima coloana egale cu zero, se va constata ca acestea formeaza un ideal stâng , fara a fi si un ideal drept. Cu toate acestea, în continuare ne vom ocupa numai de idealele bilaterale, pe care le vom numi, simplu, ideale.

Teorema 1.4.1. Daca (A, +, ) este un inel cu element unitate si IA, I , atunci (I, +, ) va fi ideal daca si numai daca satisface conditiile:

(1) Pentru orice a,b I, a + b I ;

(2) Pentru orice x A si orice a I , xa I ;

(3) Pentru orice x A si orice a I, ax I .

Demonstratie. Întrucât (i) este o conditie necesara si suficienta pentru ca (I, +) sa fie subgrup al grupului (A, +), din (i) rezula (1) . Invers, pentru orice b I , din -1 A si din (2) rezulta -b I , adica pentru orice a,b I , a + (-b) = a - b I .

Pentru fiecare inel (A, +, ) , tripletele ( ) si însasi (A, +, ) sunt exemple banale de ideale . Un ideal al lui (A, +, ) nebanal se numeste ideal propriu. Inelele fara ideale proprii se numesc inele simple . Un exemplu de inel cu ideale proprii este (Z, +, ) . Într-adevar, se constata usor ca toate subinelele acestui inel , adica tripletele (nZ, +, ) , n N , sunt ideale ale inelului numerelor întregi .

De asemenea se constata ca inelul (Q, +, ) nu admite ideale proprii , adica este simplu . De altfel , este adevarata urmatoarea afirmatie mai generala :

Teorema 1.4.2. Fiecare corp este inel simplu.

Demonstratie. Daca (I, +, ) este ideal al corpului (A, +, ) , atunci întrucât I ≠ Ř , exista a I si a ^{- 1} A astfel încât aa ^{- 1} = 1 I . Deci , oricare ar fi x A , x = x I si astfel I = A.

Mentionam ca nu orice inel simplu este obligatoriu corp, adica inelele simple nu sunt epuizate de corpuri. Pentru a ne convinge de acest lucru demonstram urmatoarea teorema :

Teorema 1.4.3. Inelul matricilor de ordin n, n > 1 , cu elemente dintr-un corp este simplu, desi acest inel nu este corp.

Demonstratie. Fie (M_n, +, ) inelul matricilor patratice de ordin n cu elemente din corpul (A, +, ) si (I, +, ) un ideal nenul al acestui inel. Deci, exista matricea care contine cel putin un element diferit de zero, de exemplu a_kl ≠ 0.

Deoarece (A, +, ) este corp, pentru orice b A exista x, y A, astfel încât b= xa_kly

Notând prin c_ij matricea din M_n care are pe locul i, j) elementul c A , iar în rest zero si tinând cont de definitia operatiei de înmultire a matricilor, pentru orice l s si orice t n,

Întrucât (I, +, ) este ideal în (M_n, +, ) , si cum orice matrice din M_n se poate reprezenta ca o suma de matrici de forma b_st , rezulta ca M_n I , adica I = M_n .

Teorema 1.4.4. Daca (I_a ), este o familie de ideale ale inelului (A, +, ), atunci este un ideal al inelului (A, +,

Demonstratie. este un subgrup al grupului aditiv (A, +) , deci ramâne sa aratam ca satisface conditiile (ii) s i (iii) din definitia idealului. Pentru aceasta, observam ca daca a , atunci a I_a , pentru fiecare a W , deci pentru orice x A si orice xa I_a , adica xa si ax .

Mentionam ca reuniunea unei familii de ideale ale unui inel nu este obligatoriu un ideal. Asa, de exemplu, se s tie ca în inelul (Z, +, ) , tripletele (2Z, +, ) si (3Z, +, ) sunt ideale, însa reuniunea lor nu este subinel al inelului (Z, +, ), deci nu va fi nici ideal în acest inel.

Teorema 1.4.5. Daca (I_a a W este o familie de ideale ale inelului (A, +, ) , atunci exista idealul (I, +, ) al inelului (A, +, ) cu proprietatile:

(i)   &nb 434g69e sp;   &nb 434g69e sp;   &nb 434g69e sp;   &nb 434g69e sp;  Pentru fiecare a W, I I_a

(ii)   &nb 434g69e sp;   &nb 434g69e sp;   &nb 434g69e sp;    Daca (I ) este ideal al inelului (A, +, ) cu proprietatea ca pentru orice a W , I I_a , atunci I I .

Idealul (I, +, ) , astfel determinat se numeste idealul generat în inelul (A, +, ) de familia de ideale (I_a ) .

Acelasi rationament ne conduce la urmatoarea afirmatie mai generala :

Teorema 1.4.6. Daca (A, +, ) este un inel si M A , atunci exista idealul (I, +, ) al inelului (A, +, ) cu proprietatile:

(1)   &nb 434g69e sp;   &nb 434g69e sp; I M;

(2)   &nb 434g69e sp;   &nb 434g69e sp; Daca idealul (I ) al idealului (A, +, ) are proprietatea I M , atunci I I.

Idealul (I, +, ) astfel determinat se numeste idealul generat în inelul (A, +, ) de submultimea M A . Evident daca M ≠ Ř , atunci idealul generat de M este idealul zero.

Prin teorema ce urmeaza obtinem constructia efectiva a idealului generat de o submultime într-un inel unitar.

Teorema 1.4.7. Daca (I, +, ) este idealul generat de submultimea M, M ≠ Ř , a inelului unitar (A, +, ), atunci elementele lui I sunt toate sumele finite de forma , unde a_i b_i A si x_i M .

Demonstratie. Daca , atunci observam ca diferenta a doua elemente din S este tot un element din S si înmultind la stânga sau dreapta un element din S cu un element din A obtinem tot un element din S, deci (S, +, ) este un ideal al inelului (A, +, ) . Deoarece (A, +, ) este inel unitar, S M , deci în baza definitiei idealului generat S I . Pe de alta parte, deoarece (I, +, ) este ideal si I M, I S deci I = S .

si în cazul idealelor, la fel ca în cazul subinelelor unui inel, se observa ca

oricare ar fi(I₁, +, ) si (I₂, +, ) ideale ale inelului (A, +, ) , I₁ I₂ Inf I₁ , I₂

De asemenea, notând prin < I₁ I₂> idealul generat de aceste doua ideale în inelul (A, +, ) obtinem ca <I₁ I₂> Sup . Prin urmare, tinând cont de definitia laticii, obtinem:

Teorema Multimea idealelor unui inel formeaza latice în raport cu

ordonarea prin incluziune.

Pentru obtinerea efectiv a a dealului generat de doua ideale ale unui inel,

formulam urmatoarea teorema :

Teorema (3.9). Daca (I₁, +, ) si (I₂, +, ) sunt ideale ale inelului (A, +, ) , atunci <I₁ I₂> este format din toate elementele de forma a +b , unde a I₁ si b I₂ .

Demonstratie. Sa notam I = si sa aratam ca I = <I₁ I₂> . Observam mai întâi ca I I₁ si I I₂ , iar I < I₁ I₂ > . Deci tinând cont de definitia idealului generat , va trebui sa demonstram numai ca (I, +, ) este ideal . (I, +) este subgrup normal al grupului aditiv (A, +) , deci pentru orice a, b , a - b I .

Apoi, daca x A si h I, atunci exista a I₁ si b I₂ , astfel încât h = a + b, deci xh = x(a + b) = xa + xb , unde xa I₁ ;i xb I₂ , adica xh I . Asemanator se arata ca pentru x A si h I , hx I .

1.5.   &nb 434g69e sp;   &nb 434g69e sp;   Inel factor (algebra pt perfectionarea prof. )

Notiunea de ideal a fost definita pornind de la proprietatile pe care le au nucleele morfismelor de inele . În continuare vom constata ca pentru orice ideal bilateral exista un morfism de inele al carui nucleu este chiar idealul dat . În acest mod , notiunea de ideal bilateral joaca în teoria inelelor acelasi rol pe care îl joaca notiunea de subgrup normal în teoria grupurilor.

Fie (A, +, ) un inel si I un ideal bilateral al sau . În particular I este un subgrup (normal) al grupului abelian (A, +) . Relatia definita pe R în modul urmator:

(1)   &nb 434g69e sp;   &nb 434g69e sp;   &nb 434g69e sp;   &nb 434g69e sp;   &nb 434g69e sp;   &nb 434g69e sp;   &nb 434g69e sp;   &nb 434g69e sp;   &nb 434g69e sp;   &nb 434g69e sp;   &nb 434g69e sp;   &nb 434g69e sp;   &nb 434g69e sp;   &nb 434g69e sp;   &nb 434g69e sp;   &nb 434g69e sp;   &nb 434g69e sp;   &nb 434g69e sp;   &nb 434g69e sp; x ≡ y (mod I) x - y I

este o relatie de echivalenta compatibila cu operatia aditiva pe R . Aceasta proprietate face posibila extinderea operatiei " + " de la elementele lui R la clasele de echivalenta în raport cu relatia " ≡ " , prin

+ =

O clasa de echivalenta în raport cu relatia " ≡ " este de forma = x + I = .

În raport cu aceasta operatie multimea R / ≡ a claselor de echivalenta are o structura de grup abelian. Elementul neutru al acestui grup este = I .

Vom studia în continuare comportarea relatiei " ≡ " în raport cu înmultirea.

1.5.1. Lema. Daca I este un ideal bilateral al inelului (A, +, ) atunci relatia de echivalenta " ≡ " definita prin (1) este compatibila cu operatia " " din inelul A.

Demonstratie. Fie x ≡ x₁ (mod I) si y ≡ y₁(mod I). Exista a, b i astfel încât x - x₁ = a I si y - y₁ = b I .

x y = (x₁ + a)(y₁ + b) = x₁y₁ + ay₁ + x₁b + ab

xy - x₁y₁ = ay₁ + x₁b + ab I

Ultima relatie rezulta din faptul ca I este ideal bilateral si arata tocmai xy ≡ x₁y₁ (mod I) .

Ca si în cazul grupurilor , multimea claselor de echivalenta în raport cu idealul I o vom nota cu A / I.

1.5.2. Teorema. Multimea A / I are o structura de inel în raport cu operatiile definite astfel :

+ =

=

Demonstratie. Pentru a nu complica scrierea am folosit notatiile " + " si " " pentru operatiile cu clase de echivalenta ca si pentru operatiile cu elementele din A de operatiile din A / I dupa natura elementelor cu care se lucreaza.

Dupa cum amamintit la începutul paragrafului , multimea A / I are o structura de grup abelian în raport cu « + ». Din lema 1.5.1. rezulta ca operatia multiplicativa cu clasele de echivalenta este bine definita. Prin calcul verificam ca aceasta operatie este asociativa :

= 

si distributiva fata de adunare :

Inelul factor (A/I, +, poarta numele de inel factor al inelului A în raport cu idealul sau bilateral I .

Daca A este inel unitar si 1 este elementul sau unitate , atunci este element unitate al inelului A/I . Într-adevar , pentru orice A/I , deducem :

= = si

De asemenea , daca A este inel comutativ , atunci printr-un calcul simplu putem arata ca si A/I este inel comutativ .

Aplicatia , definita prin

este un morfism surjectiv de inele. Într-adevar , pentru orice x, z R deducem

În plus orice element din R/I este de forma , x R .

Morfismul φ₁ poarta numele de surjectie canonica a inelului R pe inelul sau factor R/I . Nucleul acestui morfism este chiar idealul bilateral I :

Ker

Daca R este inel unitar , atunci φ₁ este morfism unitar pentru ca

1.6.   &nb 434g69e sp;   &nb 434g69e sp;   Morfisme de inele

Fie (A, +, ) si (B, +, ) doua inele . Functia f : A B se numeste morfism de inelul (A, +, ) la inelul (B, +, ) daca pentru orice a₁, a₂ A se satisfac conditiile:

(i)   &nb 434g69e sp;   &nb 434g69e sp;   &nb 434g69e sp;   &nb 434g69e sp;  f(a₁ + a₂) = f(a₁) + f(a₂)

(ii)   &nb 434g69e sp;   &nb 434g69e sp;   &nb 434g69e sp;    f(a₁a₂) = f(a₁) f(a₂) ,

adica functia este compatibila cu operatiile de adunare si de înmultire.

Acest morfism se va numi injectiv, surjectiv sau bijectiv daca functia f : A B este respectiv injectiva , surjectiva sau bijectiva. De asemenea , morfismele de la un inel (A, +, ) la el însusi se mai numesc endomorfisme, iar endomorfismele bijective se numesc automorfisme.

În continuare, daca nu va exista nici un pericol de confuzie vom nota inelul (A, +, ) simplu prin A.

Sa dam câteva exemple de morfisme de inele :

(1) Pentru fiecare inel (A, +, ) , functia 1_A : A A este un automorfism.

(2) Fie (A, +, ) un inel unitar si a A un element inversabil, adica exista a ^-1 A astfel încât a a^-1 = a^-1 a = 1. Atunci functia j_a : A A definita prin j_a(x) = axa^-1 este un automorfism . Într-adevar , pentru orice x₁, x₂ A

j_a(x₁ + x₂) = a(x₁ + x₂)a^-1 = ax₁a^-1 + ax₂a^-1 = j_a(x₁) + j_a(x₂)

si de asemenea ,

j_a(x₁ x₂) = a(x₁ x₂)a^-1 = (ax₁a^-1 )( ax₂a^-1 )= j_a(x₁) j_a(x₂)

Apoi, daca j_a(x₁) = j_a(x₂) , atunci ax₁a^-1 = ax₂a^-1 , adica a^-1 ax₁ a^-1 =a^-1 ax₂a^-1 ,

deci x₁a^-1 = x₂a^-1 si astfel x₁ = x₂ . În sfârsit , pentru orice y A , exista a^-1ya A astfel încât j_a(a^-1ya) = a(a^-1ya)a^-1 = y .

3. Fie (A, +, si (B, +, doua inele . Definind în multimea A x B doua operatii binare prin

(a₁, b₁) + (a₂, b₂) = (a₁ + a₂ , b₁ + b₂)

(a₁, b₁) (a₂, b₂) = (a₁ a₂ , b₁ b₂)

se constata imediat ca (A x B, + , ) devine inel.

Functiile i₁ : A A x B si i₂ : B A x B definite prin i₁(a) = (a, 0) si i₂(b) = (0, b) sunt morfisme injective, iar functiile p₁ : A x B A si p₂ : A x B B definite prin p ₁((a, b)) = a si p₂ ((a, b)) = b sunt morfisme surjective.

Mentionam ca daca A si B sunt inele unitare, pentru care 1 A este element unitate în A si 1^' B element unitate în B , iar f : A B este un morfism de inele , atunci morfismul f nu pastreaza obligatoriu unitatea, adica în general f(1) 1' . Daca aceasta proprietate este însa satisfacuta , vom spune ca morfismul f este unitar.

Studiem în continuare , câteva proprietati ale morfismelor de inele .

Teorema 1.6.1. daca f : A B este un morfism de la inelul A la inelul B , atunci

(1)   &nb 434g69e sp; f(0) = 0 ;

(2) f(- a) = - f(a) .

Demonstratie. Întrucât f este , în particular , un morfism de la grupul aditiv (A, +) , la grupul aditiv (B, +) , egalitatile mentionate sunt o consecinta imediata a teoremei grupurilor .

Teorema 1.6.2. Daca f : A B si g : B C sunt morfisme de inele, atunci gf : A C este morfism de la inelul A la inelul C . Mai mult , daca f si g sunt morfisme injective, surjective sau bijective, atunci la fel este si morfismul g f .

Demonstratie. Este suficient sa aratam ca se satisface a doua conditie din definitia morfismului de inele. Pentru aceasta observam ca daca a, b A , atunci

(gf) (ab) = g(f(ab)) = g(f(a) f(b)) = g(f(a)) g(f(b )) =

= (gf )(a) (gf)(b) .

Teorema 1.6.3. Daca f : A B este un morfism de inele si A₁ A este un subinel al inelului A , atunci f(A₁) este subinel al inelului B . În particular f(A) va fi subinel al inelului B , numit imaginea morfismului f si notata prin Im f.

Demonstratie. Deoarece f este morfism de la grupul aditiv al inelului A la grupul aditiv al inelului B , f(A) este un subgrup al grupului aditiv B . Ramâne de aratat ca pentru orice b₁, b₂ f(A₁), b₁b₂ f(A₁) . Pentru aceasta , observam ca exista a₁, a₂ A , astfel încât b₁ = f(a₁) si b₂ = f(a₂) , deci b₁b₂ = f(a₁) f(a₂) = f(a₁a₂) f(A₁) .

Teorema 1.6.4. Daca f : A B este un morfism de inele si B₁ B este un subinel al inelului B , atunci f ^-1(B₁) este un subinel al inelului A . În particular , f^-1() va fi un subinel al inelului A, numit nucleul morfismului f si notat prin Ker f .

Demonstratie. Se stie ca f^-1(B₁) este un subgrup la grupului aditiv (A, +) . Sa aratam ca f^-1(B₁) este chiar un subinel al inelului A. Pentru aceasta, fie a₁, a₂ f^-1 (B₁), adica f(a₁) B₁ si f(a₂) B₁ , deci f(a₁a₂) B ₁ si astfel a₁a₂ f^-1(B₁) .

Teorema 1.6.5. Daca f : A B este un morfism de inele si I B este un ideal al inelului B, atunci f^-1(I) va fi ideal în A. În particular, Ker f = f^-1 () va fi ideal în A.

Demonstratie. Din teorema precedenta rezulta ca f^-1(I) este subinel al inelului A adica prima conditie din definitia idealului este satisfacuta. Sa aratam ca se satisface si a doua conditie. Pentru aceasta, fie x A si a f^-1(I), deci

f(xa) = f(x) f(a) I si la fel f(ax) = f(a) f(x I) , prin urmare xa , ax f^-1(I) .

Mentionam ca imaginea directa a unui ideal I al inelului A prin morfismul f : A B nu este neaparat un ideal al inelului B. Cu toate acestea , este adevarata afirmatia:

Teorema 1.6.5 . Daca f :A B este un morfism de inele surjectiv si IA este un ideal al inelului A, atunci f(I) este un ideal al inelului B.

Demonstratie. Evident este suficient sa aratam ca daca y B si b f(I), atunci by I si yb f(I) . Din faptul ca b f(I) rezulta ca exista a I astfel încât b = f(a) , iar din faptul ca f este morfism surjectiv rezulta ca exista x A astfel încât y = f(x) . În plus, ax I si xa I , deci by = f(a) f(x) = f(ax) f(I) si yb = f(x) f(a) =  = f(xa) f( I ) .

Teorema 1.6.6. Morfismul de inele f : A B este injectiv daca si numai daca Ker f =

Demonstratie. Afirmatia este o consecinta a teoremei grupurilor :

« Morfismul f : G₁ G₂ este injectiv daca si numai daca Ker f =  » , teorie transcrisa în limbajul grupurilor aditive .

Teorema 1.6.7. Morfismul de inele f : A B este surjectiv daca si numai daca Im f = B .

Demonstratie. Inelele A si B se numesc izomorfe daca exista morfismele f : A B si g : B A astfel încât :

(i)   &nb 434g69e sp;   &nb 434g69e sp;   &nb 434g69e sp;   &nb 434g69e sp;  g f = 1_A ;

(ii)   &nb 434g69e sp;   &nb 434g69e sp;   &nb 434g69e sp;    f g = 1_B .

si de data aceasta se poate arata ca izomorfismul de inele poate fi caracterizat complet de notiunea de morfism bijectiv, anume :

Teorema 1.6.8. Inelele A si B sunt izomorfe daca si numai daca exista cel putin un morfism bijectiv f : A B .

Demonstratie. Daca A si B sunt izomorfe ca inele , atunci exista morfismele f si g astfel încât g f = 1_A si f g = 1_B . Se constata imediat ca f : A B este morfism bijectiv.

Invers sa presupunem ca f : A B este un morfism bijectiv de inele. Atunci, f este în particular si un morfism bijectiv de grupuri, deci exista morfismul de grupuri f^-1 : B A cu proprietatea f ^-1 f = 1_A si f f ^-1 = 1_B . Ramâne sa aratam ca f^-1 : B A este chiar un orfism de inele. Pentru aceasta, observam ca daca b₁ b₂ B , atunci f(f ^-1(b₁ b₂)) = b₁b₂ si f(f ^-1 (b₁) f ^-1 (b₂)) = f(f ^-1 (b₁)) f(f ^-1 (b₂)) deci, întrucât f este injectiva , avem f ^-1 (b₁b₂) = f ^-1 (b₁) f ^-1 (b₂) .

Teorema 1.6.9. Fiecarui ideal I al inelului A i se poate asocia un inel factor A / _I ; I un morfism surjectiv g : A A / _I astfel încât Ker g = I .

Demonstratie. În grupul comutativ (A, +) , idealul I este evident un subgrup normal. Deci , exista grupul factor A _I , unde  a + I = , iar operatia grupala se defineste prin

(a + I) + (b + I) = (a + b) + I

Sa definim în multimea cât A / _I o noua operatie binara , astfel :

(a + I) (b + I) = ab + I

Observam, mai întâi, ca operatia astfel definita nu depinde e alegerea reprezentantilor , în sensul ca daca a₁ a + I si b₁ b + I , atunci a₁b₁ + I = ab + I . Într-adevar, daca x a₁b₁ + I , atunci exista h₁ I astfel încât x = a₁b₁ + h₁ . Apoi din faptul ca a₁ a + I si b₁ b + I rezulta ca exista h₂, h₃ I astfel încât a₁ = a + h₂ si b₁ = b + h₃ , deci x = (a + h₂)(b + h₃) + h₁ = ab + ah₃ + h₂b + h₂h₃ + h₁ . Dar întrucât i este ideal , ah₃ + h₂b + h₂h₃ + h₁ I adica exista  h = ah₃ + h₂b + h₂h₃ + h₁ I astfel încât x = ab + h , deci x ab + I si astfel a₁b₁ + I ab + I . Asemanator se arata ca ab + I a₁b₁ + I .

În continuare se verifica imediat ca operatia de înmultire este asociativa , deci (A / _I , + , ) formeaza un inel . Elementul nul al inelului factor A / _I este clasa 0 + I = I , unde 0 este elementul zero din inelul (A, +,

Aplicatia g : A A _I definita prin g(a) = a + I este un morfism surjectiv , asa cum rezulta din definitia operatiilor din inelul cât .

În sfârsit, se observa ca pentru orice a A , a + I = I daca si numai daca a I , deci Ker g = = I .

Teorema 1.6.10. (Prima terema de izomorfism). Daca f : A B este morfism de inele atunci A / _{Ker f} si Im f sunt inele izomorfe.

Demonstratie. Prin teorema 1.6.5. , Ker f = f ^-1 () este ideal al inelului A deci în baza teoremei precedente exista inelul factor A _{Ker f} , unde a + Ker f ) .

Definind functia h_f : A _{Ker f} Im f prin h_f (a + Ker f ) = f(a) se constata ca h_f este morfism bijectiv , adica inelele A _{Ker f} si Im f sunt izomorfe .

Teorema 1.6.11. (Teorema a doua de izomorfism)

Fie R un inel , R un subinel al lui R si I un ideal bilateral al lui R. Atunci

R + I =

este un subinel al lui R . I este ideal bilateral al lui R + I , R I este ideal bilateral al lui R si exista un izomorfism canonic

q : R R I (R + I) I .

Demonstratie. Daca u , v R + I , atunci exista x, y R si a, b I astfel încât u = x + a si v = y + b

u - v = (x - y) + (a - b) R + I

uv = xy + (xb + ay + ab) R + I

deci R + I este subinel al lui R .

Deoarece I este ideal bilateral în R , I este evident un ideal bilateral al lui R + I . R I este subinel al lui R ca intersectie de subinele , deci este subinel al lui R

Daca x R si a I , atunci xa , ax R deoarece R este subinel si xa , ax I deoarece I este ideal bilateral . Deci xa , ax R I , adica R I este ideal bilateral al lui R . Fie i : R R + I morfismul incluziune , i(x) = x, pentru orice x R si j : R + I R + I I surjectia canonica , j(x) = x + I. Notam f = j I , f : R (R + I) I. F este morfism surjectiv de inele si Ker f = = = R I . Conform teoremei fundamentale de izomorfism , exista un izomorfism canonic

q : R / R I (R + I) / I

Acest izomorfism este definit prin q(x + R I) = x + I .

Teorema 1.6.12. ( Teorema a treia de izomorfism )

Fie R un inel , I un ideal bilateral al sau si j : R R I surjectia canonica . Notam cu J (R , I) multimea subinelelor inelului R care includ pe I si cu J (R I) multimea subinelelor inelului R I . Aplicatia F J (R , I) J (R I) definita prin F (R j (R ) = R I este o bijectie . Daca J J (R , I) , atunci J este un ideal bilateral în R daca si numai daca J I sete ideal bilateral în R I . În plus , în acest caz exista un izomorfism canonic

q : R J (R I) (J I)

Demonstratie. Deoarece j este un morfism surjectiv de inele , consideram surjectiile canonice :

Morfismul f = j _{J I} j : R (R I) (J I) este surjectiv . Pentru x R , f(x) J I daca si numai daca x + I J I sau x J . Rezulta Ker f = J si conform teoremei fundamentale exista un izomorfism canonic q : R J (R I ) (J I ) definit prin

q(x + J) = f(x) = (x + I) + J I .

Aplicatie . Ne propunem sa descriem ideale si inele factor ale inelului claselor de resturi modulo n .În inelul Z al numerelor întregi multimea nZ , n N este ideal (bilateral) .Fie j_n : Z Z_n surjectia canonica . Exista o bijectie între multimea J (Z, nZ) a idealelor lui Z care includ nZ si multimea J (nZ) a idealelor lui Z_n . atunci I = j_n (J) este un ideal al lui Z care include nZ , deci I = mZ si m n (mZ nZ m n) . Din egalitatea J = j_n(I) rezulta J = (mZ) (nZ) .Deci idealele (bilaterale ) ale inelului Z_n sunt de forma (mZ) (nZ) unde m n . Conform teoremei a treia de izomorfism exista un izomorfism

q : Z mZ Z_n (mZ nZ) .

Rezulta ca inelele factor ale inelului Z_n sunt izomorfe cu inele de forma Z_m , unde m n .

1.7. Inele de fractii

O notiune importanta în teoria structurilor algebrice, în particular în teoria

inelelor, este aceea de scufundare izomorfa . Anume, vom spune ca inelul (A, +, ) se scufundă izomorf în inelul (B, +, ) daca exista un morfism injectiv f : A B .

Evident, în acest caz f(A) este un subinel al inelului B izomorf cu inelul A.

În leg a tura cu aceasta notiune este adevarata urmatoarea afirmatie:

Teorema 1.7.1. Fiecare inel se scufunda izomorf într-un inel cu unitate.

Demonstratie. Fie inelul (A, +, ) si sa notam B = A x Z , unde Z este

multimea numerelor întregi. În multimea B s a definim doua operatii binare, notate tot prin + si astfel

(a₁, n₁) + (a₂, n₂) = (a₁ + a₂ , n₁ + n₂)

(a₁, n₁) (a₂, n₂) = (a₁a₂ + n₂a₁ , n₁n₂)

Se constata ca (B, +, ) este un inel care poseda ca element unitate perechea (0,1) .

Functia f : A B definita prin f(a) = (a, 0) este un morfism injectiv de la

inelul (A, +, ) la inelul (B, +, ) . Într-adevar, faptul ca aceasta functie este injectiva este evident, apoi observam ca pentru orice a b A

f(a + b ) = (a + b ,0 ) = (a, 0) + (b, 0) = f(a) + f(b)

f(ab) = (ab, 0) = (a, 0) (b, 0) = f(a) f(b) .

Prin urmare , inelul (A, +, ) se scufunda izomorf în inelul cu unitate (B ,

O alta teorema de scufundare, deosebit de importanta în teoria inelelor, este

urmatoarea:

Teorema 1.7.2. Fie (A, +, ) un inel comutativ si cu element unitate si fie S

multimea tuturor elementelor din A care nu sunt divizori ai lui zero. Atunci exista inelul (, +, ) comutativ si cu element unitate si morfismul injectiv  f : A A astfel încât toate elementele din f(S) sunt inversabile în inelul (,+ ,

Demonstratie. Observam, mai întâi, ca S Ř, deoarece cel putin elementul

unitate din inelul (A, +, ) apartine lui S (adica 1 S ) si ca , daca s₁, s₂ S, atunci s₁s₂ S .

Apoi, se demonstreaza usor ca , relatia binara definita în produsul cartezian A x S prin

(a₁, s₁) (a₂, s₂) a₁s₂ = a₂s₁

este o relatie de echivalenta în multimea A x S . Deci, exista multimea cât A x S ~ pe care sa o notam prin , adica , unde

Definind în multimea cât A operatiile binare prin + si prin

() + () = ()

() () = ()

se constata ca operatiile de adunare si înmultire astfel definite nu depind de alegerea reprezentantilor claselor. Mai mult, (,+ , ), devine inel comutativ, care poseda ca element unitate clasa () .

Functia f :A A, definita prin f( a) = ( ) este un morfism injectiv de la inelul (A,+ , ) la inelul (,+ , ) . Într-adevar, daca f(a₁) = f(a₂) , atunci , adica (a₁,1) (a₂.1), deci a₁ 1 = a₂ 1 si astfel a₁ = a₂ , prin urmare aplicatia f este injectiva . Apoi, observam ca oricare ar fi a₁, a₂ A

f (a₁ + a₂) = () = () + () = f(a₁) + f( a₂)

f (a₁a₂) = () = () () = f(a₁) f(a₂) .

Pentru a termina demonstratia, ramâne sa aratam ca elementele din f(S) sunt

inversabile în inelul (,+ , ) . Daca b f(S) , atunci exista s S astfel încât  b = f(s)= () deci f(S) = . Cu aceasta precizare , observam ca oricare ar fi clasa () f (S) , exista clasa () A astfel încât () () = () .

De obicei elementele inelului se noteaza simplu prin , în loc de () , adica = . Acest inel se numeste inelul de fractii al inelului (A, +,

În cazul când inelul (A, +, ) este domeniu de integritate, atunci inelul sau de

fractii (,+ , ) este chiar un corp, deci:

Teorema 1.7.3. Fiecare domeniu de integritate se scufunda izomorf într-un

corp, numit corpul de fractii al domeniului de integritate respectiv.

Pentru exemplificare, sa ne reamintim cum a fost construit corpul

numerelor rationale (Q,+ , ) . Vom constata ca (Q,+ , ) este corpul de fractii al

domeniului de integritate (Z,+ ,

1.8. Inele de polinoame.

Inelul polinoamelor intr-o nedeterminata.

Fie A un inel comutativ si unitar. Vom face o constructie a inelului de polinoame intr-o nedeterminata peste A, care la început nu foloseste scrierea obisnuita a polinoamelor cu ajutorul unei nedeterminate X.

Peste inelul A se considera sirurile f = (a0, a1, a2, .), ai A a.i. toti termenii sai, in afara de un numar finit dintre ei, sunt nuli.

Fie A' multimea tuturor sirurilor de acest tip. sirurile f = (a0, a1 , .) si g = (b0 , b1 , .) sunt egale daca si numai daca ai = bi, pentru orice i. Pentru A' se definesc doua operatii algebrice , adunarea si înmultirea, in raport cu care A' devine un inel comutativ si unitar.

Fie f, g A', f = (a0, a1, a2, .) , g = (b0, b1, b2,.). Atunci adunarea se defineste astfel: f + g = (a0 + b0, a1 + b1, a2 + b2, .).

Este evident ca f + g are numai un numar finit de termeni nenuli, deci f + g A . Sa verificam ca (A',+) este grup abelian .

Într-adevar , daca f ,g, h A , f = (a0, a1, a2, .), g = (b0, b1, b2, .), h = (c0, c1, c2, .), atunci (f + g) + h = (a0 + b0, a1 + b1, a2 + b2, .) + + (c0, c1, c2, .) = [(a0 + b0) + c0, (a1 + b1) + c1, .] si f + (g + h) = (a0, a1, a2, .) + [(b0, b1, b2, .) + (c0, c1, c2,.)] = [a0 + (b0 + c0),a1 + (b1 + c1),.] .

Cum adunarea in inelul A este asociativa ,avem (ai + bi) + ci = ai + (bi + ci) , i = 1, 2, 3 ., de unde (f + g) + h = f + (g + h) . Analog se arata ca f + g = g + f.

Daca 0 = (0, 0, 0, .) , atunci 0 + f = (0, 0, .) + (a0, a1, .) = (0 + a0, 0 + + a1, .) = (a0, a1, a2, .) = f = f + 0, deci 0 este element neutru pentru adunare. Daca f A', f = (a0, a1, a2, .), atunci -f = (- a0, - a1, - a2, .) este opusul lui f si f + (- f) = (- f) + f = 0 .

Înmultirea pe A se defineste astfel:

F g = (a0b0, a0b1 + a1b0, a0b2 + a1b1 + a2b1, .) = (c0, c1, .) , unde Ck=.

Este clar ca f, g A'. Înmultirea pe A', astfel definita , este asociativa, comutativa si are element unitate. Sa aratam mai întâi asociativitatea .

Fie f, g, h A' , unde f = (a0, a1, a2, .) , g = (b0, b1, b2, .) , h = (c0, c1, ,c2, .) si sa aratam ca (fg)h = f(gh).

Fie fg = (d0, d1, d2,.). Atunci . De asemenea, fie

(fg)h = (d0',d1',d2',.), unde d'm =

Daca gh = (c0,c1,.), atunci :

si fie f(gh) = (l'0,l'1,l'2,.), unde :

.

Deci d'm = l'm pentru orice m. Deci (fg)h = f(gh) . Comutativitatea înmultirii rezulta din faptul ca înmultirea in inelul A este comutativa, iar in expresia produsului polinoamelor f si g termenii factorilor intervin in mod simetric.

Elementul unitate din A' este sirul (1, 0, 0, .) . Înmultirea pe A' este distributiva fata de adunare. Într-adevar, cu notatiile de mai sus, rezulta :

f(g + h) = (d0, d1,.) , unde

fg + fh = (d'0,d'1,.), unde

Cum operatia de înmultire pe A este distributiva fata de adunare rezulta f(g + h) = fg + fh. Evident are loc si relatia (f + g)h = fh + gh si afirmatia s-a demonstrat.

Propozitia 1.8.1.

Daca A este un inel unitar comutativ, atunci multimea A' ( a sirurilor de elemente din A, care au numai un numar finit de termeni nenuli) împreuna cu operatiile de adunare si înmultire definite mai sus este un inel comutativ si unitar.

Elementele acestui inel se numesc polinoame peste A sau polinoame cu coeficienti din A .

Daca f = (a0, a1, .) este un polinom nenul (adica nu toti termenii ai sunt nuli ) si daca n este cel mai mare numar natural cu proprietatea ca an 0 , atunci n se numeste gradul polinomului f . Pentru polinomul nul nu se defineste gradul. Convenim sa consideram gradul sau ca fiind - . Daca gradul (f) = n , atunci a0, a1, ., an se numesc coeficientii polinomului f.

Fie aplicatia u: A A' definita prin u(a) = (a, 0, 0, .) . Aplicatia u este injectiva , caci, daca u(a) = u(b), atunci (a, 0, .) = (b, 0, .) a = b. De asemenea , u(a + b) = u(a) + u(b) si u(ab) = u(a)u(b) , " a, b A , deoarece , dupa definitie , este evident ca (a, 0, .) + (b, 0, .) = (a + b, 0, . ) si (a, 0, .) (b, 0, .) = (ab, 0, .) .

Deci u este omomorfism injectiv. Acest fapt permite sa se identifice elementul a A cu imaginea sa prin u , adica polinomul (a, 0, .) din A'. Astfel, A se poate considera ca un subinel al lui A'. Notam prin X polinomul (0, 1, 0, .), care se numeste nedeterminata X. Obtinem:

Pentru orice a A, avem ax= (0, 0, ., 0, a, 0, .). Fie acum un polinom de gradul n , f = (a0, a1, a2, ., an, 0, .) = (a0, 0, 0, .) + (0, a1, 0, .) + .

.+ (0, 0, .an, 0, .) = a0(1, 0, .) + a1(0, 1, 0, .) + . + an(0, 0, ., 1, 0, .) =

Daca an = 1 , spunem ca polinomul este unitar. Inelul A' obtinut se numeste inelul polinoamelor in nedeterminata X cu coeficienti in inelul A (sau peste inelul A) si se noteaza cu A[X]. Observam ca f are gradul 0 sau - daca si numai daca f apartine inelului A. Din definitia sumei si produsului a doua polinoame , rezulta ca grad (f + g) max (grad(f), grad(g)) ; grad(fg) grad(f) + grad(g), pentru " f, g A[x].

Daca A este un domeniu de integritate , se poate înlocui a doua inegalitate printr-o egalitate.

Propozitia 1.8.2.

Daca A este un domeniu de integritate, atunci inelul de polinoame A[x] este domeniu de integritate.

Demonstratie

Fie f, g A[x] ;

Atunci :

A fiind domeniu de integritate, rezulta din am 0 si bn 0 ca ambn 0, adica fg 0. În particular , pentru un corp comutativ K, inelul polinoamelor de o nedeterminata cu coeficienti in K este un inel integru.

Propozitia 1.8.3.

Fie A un domeniu de integritate si A[x] inelul polinoamelor in nedeterminata X cu coeficienti in A. Atunci elementele inversabile ale inelului A[x] coincid cu elementele inversabile ale inelului A. deci, cu notatiile cunoscute, avem: u(A[x]) = =u(A).

Demonstratie:

Fie a A, inversabil in A , adica exista b A a.i. a b = 1. Evident, aceasta relatie are loc si in A[x] , deoarece a si b sunt polinoame de gradul zero, deci a este inversabil in A[x].

Invers, fie f un polinom din A[x] inversabil. Atunci exista un polinom g A[x] a.i. fg = 1 si , deci, grad(f) + grad(g) = grad(1) = 0, adica f, g A. Deci f A si f este inversabil in A. In particular, pentru un corp comutativ K, polinoamele inversabile din K[x] sunt polinoame de gradul 0 si numai acesta. Daca A nu este domeniu de integritate, putem avea u(A[x]) u(A). Intr-adevar , polinomul neconstant 1 + 2X Z [x] este inversabil, deoarece (1+2x)(1+2x) = 1.

Exemple . ( Probleme )

1.   &nb 434g69e sp;  Sa se arate ca in inelul Q[x, y], polinomul x + y este ireductibil.

Solutie.

Este clar ca x + y este nenul si neinversabil . Daca ar fi reductibil s-ar descompune astfel: x + y = (a + a x + a y)(b + b x + b y) = a b + (a b + a b )x + + (a b + a b )y + (a b + a b )xy + a b x + a b y . De aici obtinem a b = 0, a b = 1 ,

a b = 1, a b + a b = 0 de unde a = b = 0. Apoi, din a a (a b + a b ) = 0 se obtine se obtine ca a + a = 0, contradictie .

2. Sa se arate ca in inelul C[X, Y] , polinomul X (Y + 1) + X Y + X Y + + XY + Y este ireductibil, n 2 , n N .

Solutie .

Polinomul poate fi considerat in nedeterminata X cu coeficienti in Q[Y] deci, in inelul Q[X][Y]. Atunci, pentru valoarea particulara y = p, p - prim , in inelul factorial Q[Y] sunt îndeplinite conditiile din criteriul lui Eisenstein . Deci, polinomul X (Y+1) +X Y +X Y +XY +Y este ireductibil in inelul Q[X][Y] = Q[X,Y] .

3. Sa se arate ca polinomul f = 3X + 4X - 6X + 7X + 21 este ireductibil in Z[X] .

Solutie .

Polinomul f este primitiv. Aplicam criteriul reductiei pentru p=2. Avem f = X +X +1 Z [X] si aratam ca f este ireductibil in Z [X]. Deoarece f(0) = (1) = 1 0 , rezulta ca f nu are factori de gradul întâi in descompunere. Fie acum X +X +1= (aX + bX + c)(mX + nx + pX + q). Prin identificarea coeficientilor se ajunge la am = 1, an + mb = 0, ap + bn + cm = 0, aq + bp + cn = 1, cq = 1. De aici, avem a = m = c = q = 1 si deci, b + n = 0, p + bn = 1, bp + n = 1, b + p = 0, de unde, prin calcul simplu ajungem la a = 1, contradictie. In concluzie, f este ireductibil in Z [X]. Din criteriul reductiei rezulta f ireductibil in Z[X].

Inelul polinoamelor de mai multe nedeterminate.

Fie A un inel. Atunci inelul polinoamelor in nedeterminatele X1, X2, ., Xn cu coeficienti in inelul A se defineste inductiv astfel : daca A[X1] este inelul polinoamelor in nedeterminata X , cu coeficienti in inelul A1, A[X1, X2] este inelul polinoamelor in nedeterminata X2 cu coeficienti in inelul A[X1] si, in general : A[X1, X2, ., Xn] este inelul polinoamelor in nedeterminata Xn cu coeficienti in inelul A[X1, X2, ., Xn-1] . Pe A[X1] l-am construit deja si in mod recurent:

A[X1,X2]=A[X1]A[X2]

A[X1,X2,X3]=A[X1,X2]A[X3] ;

A[X1,X2,.Xn]= A[X1,X2,.,Xn-1]A[Xn].

Daca f este un polinom in inelul A[X1,X2,.,Xn] , atunci el este polinom in nedeterminata Xn cu coeficienti in inelul A[X1,X2,.,Xn-1] si , deci, A[X1,X2,.,Xn-1], pentru orice i=0, 1, ., hn . Din aproape in aproape , f se scrie ca o suma finita de forma:

în care A se numesc coeficientii polinomului f,

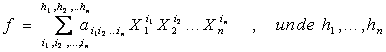sunt numere nenaturale . Un polinom din A[X1, X2, . Xn] de forma aX1X2X3 . Xn, a 0 , se numeste monom .

Definitie

Se numeste gradul monomului aX1X2X3.Xn, a 0 in raport cu ansamblul nedeterminatelor X1,X2,X3,.,Xn, suma i1+i2+.+in.

Definitie:

Se numeste gradul polinomului f A[X1,X2,.Xn] in raport cu ansamblul nedeterminatelor X1,.,Xn cel mai mare dintre gradele monoamelor sale in raport cu ansamblul nedeterminatelor. Ca si in inelul polinoamelor intr-o nedeterminata , si aici avem:

Propozitia 1.8.4.

Fie A un inel si f,g A[X1,X2,.Xn]. Atunci:

grad(f + g) max(grad(f), grad(g)) ;

grad(fg) grad(f) + grad(g) ;

daca, in plus, A este domeniu de integritate , atunci la punctul (2) vom avea egalitate ; mai mult, U(A[X1, X2, . Xn]) = U(A).

1.9. Inelul claselor de resturi modulo n

Operatiile de adunare si înmultire confera multimii Z a numerelor întregi o structura de inel comutativ unitar si fara divizori ai lui zero .(pe scurt inel integru ) .În acest inel multimea nZ a multiplilor numarului natural n (fixat) formeaza un ideal (bilateral) . Pe de alta parte daca I este un ideal al inelului (Z, +, ) atunci I este un subgrup al grupului (Z, +) deci exista un numar natural n astfel încât I = nZ . Daca I = nZ si J = mZ sunt doua ideale ale lui Z atunci I + J este de asemenea un ideal al lui Z si exista d Z astfel încât I + J = dZ sau nZ + mZ = dZ (putem presupune d N) . Din relatia n m dZ rezulta d n si d m , iar din relatia d nZ + mZ rezulta ca exista a, b Z astfel încât d = an + bm . Din urma relatiei deducem ca orice divizor comun al lui m si n este si un divizor al lui d . Prin urmare d este cel mai mare divizor comun al numerelor întregi n si m . Analog se demonstreaza ca daca nZ mZ = qZ atunci q este cel mai mic multiplu comun al lui n si m . De asemenea are loc relatia (nZ)(mZ) = (nm)Z .

Inelele factor ale inelului Z se construiesc prin factorizare cu ideale care au forma nZ , n N . Reamintim ca pornind de la structura de grup aditiv a lui Z si considerând un subgrup nZ al acestuia , relatia

x y x - y nZ

este o relatie de echivalenta (numita si relatie de congruenta modulo n ) si notata în teoria numerelor prin x z (mod n) ale carei clase de echivalenta au forma

Clasele de echivalenta se mai numesc si clase de resturi modulo n , în rolul reprezentantului r putând fi ales totdeauna un numar natural cuprins între 0 si n - 1 . Multimea acestor clase Z_n = capata o structura de grup comutativ în raport cu operatia Constructia amintita tine seama numai de operatia de adunare pe Z . Ţinând cont si de operatia de înmultire din Z , deci de structura de inel , se poate completa si structura lui Z_n . Astfel operatia

împreuna cu operatia de adunare induc pe Z_n o structura de inel comutativ si unitar . Acest inel poarta numele de inelul claselor de resturi modulo n . Elementele remarcabile ale acestui inel sunt urmatoarele : 0 - elementul neutru (al operatiei de adunare ) , - opusul clasei , - elementul unitate (al operatiei de înmultire ) .

Aplicatia j_n : Z Z_n definita prin j_n (x) = este un morfism unitar de inele deoarece :

Morfismul j_n se numeste surjectia canonica a lui Z pe inelul sau factor Z_n . Daca n = 0 atunci fiecare clasa de resturi în Z₀ este de forma . Surjectia canonica j = Z Z₀ este si injectiva , deci inelele Z si Z₀ sunt canonic izomorfe .

Daca n = 1 atunci = Z , deci toate numerele întregi fac parte dintr-o singura clasa de resturi , iar inelul Z₁ este inelul nul , Z₁ = .

Inelul Z_n are mai multe aplicatii în teoria numerelor . În continuare , pe baza proprietatilor grupurilor finite vom deduce câteva astfel de rezultate . Pentru aceasta vom stabilii mai întâi care sunt unitatile (elementele inversabile ) inelului Z_n .

Teorema 1.9.1. În inelul Z_n , n > 1, elementul este inversabil daca si numai daca x si n sunt relativ prime .

Demonstratie. Observam mai întâi ca daca x si n sunt relativ prime si y = x + kn , k Z_n , atunci z si n sunt de asemenea relativ prime. Daca este inversabila în Z _n atunci exista Z _n astfel încât , de unde xz = 1 + kn , pentru un anumit k Z . Din relatia

xz - kn = 1

rezulta ca divizorii comuni ai lui x si n sunt 1 , deci x si n sunt relativ prime . Reciproc , daca x si n sunt relativ prime , atunci exista numerele întregi a si b astfel încât ax + bn = 1 .Luând imaginile acestor elemente prin surjectia canonica j_n si tinând seama ca j_n (n) = 0 rezulta , adica este inversabila în Z_n .

Conform teoremei precedente , de exemplu , în Z₁₅ , si sunt inversabile , dar nu este inversabila .

1.9. 2. Consecinta . Daca n este numar prim , atunci Z_n este corp . Într-adevar daca n este numar prim , atunci 1, 2, . . n - 1 sunt relativ prime cu n si deci toate elementele inelului Z_n diferite de elementul neutru al adunarii () sunt inversabile .

1.9.3. Consecinta . Inelul Z_n (n > 1) contine atâtea elemente inversabile câte numere naturale mai mici ca n si prime cu n exista , adica j (n) elemente , unde j : N N este functia lui Euler .

1.9.4. Observatie . Legatura dintre elementele inversabile din Z_n si j (n) ne permite sa dam o noua demonstratie faptului ca indicatorul lui Euler este o functie multiplicativa . Pentru aceasta vom demonstra lema care urmeaza .

1.9.5. Lema . Daca m₁ si m₂ , sunt numere întregi relativ prime , atunci .

Demonstratie . Consideram functia f : Z Z_m1 x Z_m2 , definita prin f (x) = (j (x ) , j (x)) , unde j j sunt surjectiile canonice ale lui Z pe Z_m1 , Z_m2 . Se verifica imediat ca f este morfism de inele . Daca x Ker f , atunci m₁ x , m₂ x , si deoarece m₁ , m₂ sunt relativ prime , deducem m₁m₂ x . Daca m₁m₂ x , atunci x Ker f . Deci Ker f = m₁m₂ Z . Conform teoremei fundamentale de izomorfism Im f Z Ker f = Z_m1m2 . Deoarece Im f are m₁m₂ elemente rezulta ca Im f = Z_m1 x Z_m2 , de unde izomorfismul din enunt .

Aplicând propozitiile din 1.9.5. pentru izomorfismul din lema precedenta se obtine U(Z_m1m2) u (Z_m1) x U (Z_m2) din care deducem ca j( m₁m₂ ) = j(m₁) j(m₂) .