Masurarea tendintei centrale si a variatiei

MASURAREA TENDINTEI CENTRALE SI A VARIATIEI

Pentru a putea caractetiza o distributie este necesara definirea unor indicatori statistici, care sa descrie distributia din punct de vedere cantitativ.

Astfel, avem de-a face cu indicatori ai tendintei centrale(media, mediana, valoarea modala), care descriu distributia la nivel mediu, indicatori ai variatiei(dispersia, abaterea standard, coeficientul de variatie), care descriu distributia din punctul de vedere al omog 747g67h enitatii si indicatori de asimetrie(coeficientul de asimetrie), care descriu distributia din punctul de vedere al situarii fata de distributia normala.

Pentru o prezentare exhaustiva se recomanda consultarea bibliografiei. Am ales sa ilustram acesti indicatori printr-un exemplu rezolvat in EXCEL.

EXEMPLU

Datele din fisierul Xr04_50.xls reprezinta salariile anuale(in dolari) ale unor indivizi dupa nivelul studiilor absolvite: liceu, masterat, doctorat.

Cum putem analiza din punct de vedere statistic aceasta distributie?

Sa luam drept exemplu distributia salariului celor care au absolvit doar liceul.

Vom rezolva problema folosind EXCEL.

In primul rind, avem o reprezentare grafica a distributiei prin intermediul histogramei.

Folosim meniul ToolsData AnalysisHistogram.

Trebuie sa alegem cu mouse-ul zona de date(trebuie bifat LABELS IN FIRST ROW daca selectam si numele varabilei).

BIN se refera la capetele intervalelor pe care vor fi grupate datele. Putem sa nu selectam nimic, EXCEL realizeaza automat gruparea pe intervale. De asemenea, trebuie selectata optiunea Chart Output.

Rezultatele pentru variabila LICEU sint prezentate mai jos.

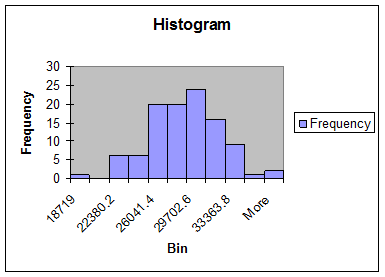
Analiza histogramei ne ofera informatii privind distributia: putem vedea ca nivelul salariului celor care au absolvit doar liceul este o variabila ce urmeaza o distributie aproape normala(are forma clopotului lui Gauss).

In continuare vom calcula indicatorii ce caracterizeaza o distributie.

Pentru aceasta folosim meniul ToolsData AnalysisDescriptive Statistics.

La fel selectam zona de date, bifam LABEL daca am selectat si numele variabilei; de asemenea, vom bifa Summary Statistics.

Rezultatele sint prezentate mai jos.

Cum interpretam valorile obtinute?

Mean – este media aritmetica - arata nivelul salariului mediu din acest esantion.

Sample Variance – dispersia de esantion, calculata dupa formula 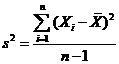- arata gradul de imprastiere a valorilor in jurul mediei; cu cat e mai aproape de zero, cu atit distributia e mai omogena.

Standard Deviation – abaterea standard, calculata ca radacina patrata a dispersiei de esantion: 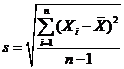- arata cu cit se abat, in medie, valorile de la media distributiei.

Standard Error – eroarea standard – calculata ca - utilitatea o vom vedea ceva mai tirziu.

Median – mediana – este acea valoare aflata in mijlocul distributiei. E.g. in cazul nostru 50% dintre persoanele din esantion au un salariu anual mai mic decit 27765 dolari si 50% au un salariu anual peste aceasta valoare.

Mode – valoarea modala – valoarea de frecventa maxima. In cazul nostru cei mai multi angajati au un salariu anual de 28539 dolari.

Kurtosis – coeficientul de aplatizare(boltire) - 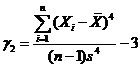; valoarea zero indica o distributie normala – in cazul nostru este 0.55, ceea ce arata o distributie apropiata de cea normala.

Skewness – coeficientul de asimetrie - - valoarea zero indica o distributie perfect simetrica; in cazul nostru distributia este foarte aproape de simtria perfecta.

Range – amplitudinea variatiei: .

Minimum - .

Maximum - .

Sum - .

Count – n – volumul esantionului.

De asemenea, avem asa-numitele cuantile, valori ale variabilei care impart distributia in intervale de frecvente egale. Mediana este cuantila de rangul doi, intrucit imparte distributia in doua intervale de frecvente egale.

Se folosesc in practica cuartilele, acele valori care impart distributia in patru intervale de frecvente egale: (la stinga ei sint 25% dintre valori), (mediana), (la stinga sint 75% dintre valori).

Pentru determinarea valorilor extreme se foloseste diagrama Box(BOX-Plot).

Aceasta a fost folosita pentru prima data de statisticianul Tukey.

Pentru intocmirea diagramei box-plot se procedeaza dupa cum urmeaza:

Se reprezinta partea centrala a seriei de distributie, cuprinsa intre cele doua cuantile extreme, ce insumeaza 50 % din valori, printr-un dreptunghi. Astfel, cele doua cuantile sunt reprezentate prin linii orizontale. Pentru definirea dreptunghiului, acestea sunt unite prin doua linii verticale.

In interiorul acestui dreptunghi se traseaza, printr-o linie orizontala, mediana seriei. Pozitia acestei linii orizontale in raport cu cele doua linii ce corespund cuantilelor extreme ofera informatii cu privire la asimetria seriei de distributie.

Pentru a vizualiza celelalte valori din cadrul seriei se adauga dreptunghiului doua segmente verticale, ce corespund valorilor adiacente partii centrale a seriei. Acestea sunt egale cu

Se vizualizeaza valorile aberante din cadrul seriei printr-o stea. Se considera ca o valoare nu este aberanta, daca aceasta se pozitioneaza in intervalul urmator de valori Valorile extreme sunt reprezentate in diagrama box-plot, dupa caz, la dreapta sau la stanga celor doua segmente, dupa cum fiecare valoare este mai mare decat , respectiv, mai mica decat .

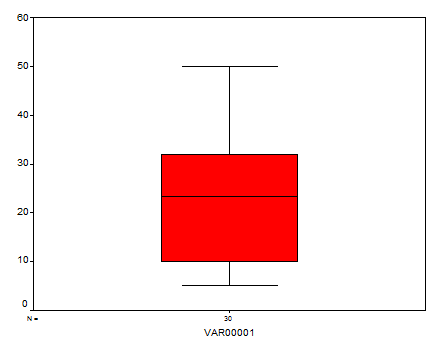
Diagrama BOX