ALTE DOCUMENTE
|
||||||||||
MATEMATICI APLICATE ÎN ECONOMIE
1. Spatiile vectoriale sunt cazuri particulare de:
a) multimi de functii
b) grupuri abeliene
c) multimi de izomorfisme
2. Spatiile vectoriale au:
a) aceeasi dimensiune
b) acelasi numar de elemente
c) aceleasi tipuri de subspatii
3. Valorile proprii ale unui operator sunt solutii:
a) ale
ecuatiei ![]()
b) ale unei ecuatii de gradul 2
c) ale unei ecuatii diferentiale
4. La o PPL conditiile de pozitivitate sunt valabile pentru:
a) o parte din necunoscute
b) nici o necunoscuta
c) toate necunoscutele
5. Un sir de numere este:
a) o multime ordonata natural
b) un spatiu bidimensional
c) o functie
6. Limita unei functii într-un punct se calculeaza daca punctul este:
a) din afara domeniului de definitie
b) punct de acumulare al domeniului de definitie
c) punct aderent al domeniului de definitie
7. În ![]() se considera o
baza:
se considera o
baza: ![]() Scrieti matricea de trecere de la baza canonica a
spatiului
Scrieti matricea de trecere de la baza canonica a
spatiului ![]() la aceasta
baza B.
la aceasta
baza B.
a) 
b) 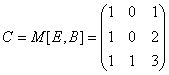
c) 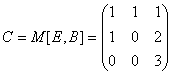
8. Precizati daca urmatoarea definitie:
"Un sistem de vectori ![]() formeaza o
baza a spatiului vectorial V daca:
formeaza o
baza a spatiului vectorial V daca:
i) B este sistem de vectori liniar dependenti
ii) B este sistem de generatori pentru V" este:
a) corecta
b) incorecta
c) incompleta
9. Sa se determine vectorul normat din ![]() ortogonal vectorilor:
ortogonal vectorilor: ![]()
a) ![]()
b) ![]()
c) ![]()
10. Criteriul general al lui Cauchy "Seria ![]() este convergenta daca si numai daca
este convergenta daca si numai daca ![]() astfel încât
astfel încât ![]() " este:
" este:
a) corect
b) incomplet
c) incorect
11. Seria ![]() este convergenta
daca si numai daca:
este convergenta
daca si numai daca:
a) ![]()
b) ![]()
c) ![]()
12. Criteriul raportului al lui D'Alembert: "Fie seria ![]() si fie
si fie ![]()
Daca ![]() seria este convergenta
seria este convergenta
Daca ![]() seria este divergenta
seria este divergenta
Daca ![]() nu se poate stabili natura seriei pe baza acestui criteriu"
este:
nu se poate stabili natura seriei pe baza acestui criteriu"
este:
a) incorect
b) corect
c) incomplet
13. Operatorul Laplace este:
a) operator de derivate partiale de ordin I
b) operator de derivate partiale de ordin II
c) operator de derivate partiale de ordin III
14. Diferentiala functiei ![]() este:
este:
a) ![]()
b) ![]()
c) ![]()
15. Care este valoarea integralei Euler - Poisson 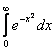 ?
?
a) 
b) 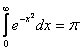
c) 
16. Sa se studieze natura seriei: ![]()
a) Seria este divergenta
b) Seria este convergenta
c) Seria este absolut convergenta
17. Sa se calculeze integrala: 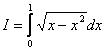
a) ![]()
b) ![]()
c) ![]()
18. Sa se calculeze integrala dubla: 
a) ![]()
b) ![]()
c) ![]()
19. Sa se integreze ecuatia diferentiala:
![]()
a) ![]()
b) ![]()
c) ![]()
20. Sa se calculeze suma seriei de termen general:
![]()
a) ![]()
b) ![]()
c) ![]()
21. Un sistem de vectori care contine vectorul nul:
a) este sistem de generatori
b) este baza
c) nu este liniar independent
22. Orice spatiu metric este:
a) spatiu compact
b) spatiu normat
c) spatiu Euclidian
23. În metoda Gauss -
a) un element pozitiv
b) un element nenul
c) un element negativ
24. Unei valori proprii îi corespunde:
a) un unic vector propriu
b) exact trei vectori proprii
c) o infinitate de vectori proprii
25 Criteriul de convergenta al functiilor rationale se refera la:
a) rapoarte de numere rationale
b) raport de polinoame
c) raport de functii trigonometrice
26. În programul optim necunoscutele secundare se completeaza cu:
a) elemente negative
b) zerouri
c) elemente pozitive
27. În spatiul Euclidian ![]() unde
unde ![]() este produsul scalar usual, se considera vectorii
este produsul scalar usual, se considera vectorii ![]() Care din afirmatiile de mai jos este
adevarata?
Care din afirmatiile de mai jos este
adevarata?
a) vectorii sunt ortogonali
b) vectorii nu sunt ortogonali
c) vectorii sunt ortonormati
28. Fie operatorul liniar ![]()
 . Sa se calculeze
. Sa se calculeze ![]() unde
unde ![]()
a) ![]()
b) ![]()
c) ![]()
29. Un punct interior lui A, ![]() în care
în care ![]() este diferntiabila, iar diferentiala sa este
nula se numeste:
este diferntiabila, iar diferentiala sa este
nula se numeste:
a) punct de maxim local
b) punct de extrem local
c) punct stationar
30. Stabiliti care afirmatie este adevarata:
a) O serie convergenta este întotdeauna absolut convergenta
b) O serie convergenta nu este întotdeauna absolut convergenta
c) O serie absolut convergenta nu este întotdeauna convergenta
31. Sa se stabileasca natura seriei de termen
general: 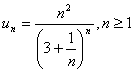
a) Seria este divergenta
b) Seria este convergenta
c) Seria este absolut convergenta
32. Se considera operatorii:
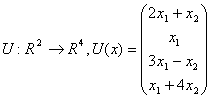 unde
unde 
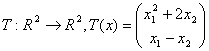 unde
unde 
Care din urmatoarele afirmatii este adevarata?
a) U este operator liniar si T nu este operator liniar
b) ambii operatori sunt liniari
c) U nu este operator liniar si T este operator liniar
33. Criteriul radacinii al lui Cauchy "Fie seria ![]() si fie
si fie ![]()
Daca ![]() seria este convergenta
seria este convergenta
Daca ![]() seria este divergenta
seria este divergenta
Daca ![]() nu se poate stabili natura seriei pe baza acestui criteriu"
este:
nu se poate stabili natura seriei pe baza acestui criteriu"
este:
a) incomplet
b) corect
c) incorect
34. Matricea hessiana pentru o functie reala de n variabile reale contine derivate partiale:
a) de ordinul unu
b) de ordinul doi
c) de ordinul n
35. Sa se calculeze suma seriei de termen general ![]()
a) ![]()
b) ![]()
c) ![]()
36. Sa se integreze ecuatia diferentiala
![]()
a) ![]()
b) ![]()
c) ![]()
37. Sa se calculeze integrala 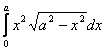
a) ![]()
b) ![]()
c) ![]()
38. Relatia de recurenta a functiei ![]() este:
este:
a) ![]()
b) ![]()
c) ![]()
39. Diferentiala de ordinul II pentru functia ![]() este:
este:
a) ![]()
b) ![]()
c) ![]()
40. Sa se calculeze: ![]() unde
unde ![]()
a) ![]()
b) ![]()
c) ![]()
41. În forma standard a unei PPL sistemul de restrictii este format:
a) din ecuatii
b) din inecuatii
c) si din ecuatii si din inecuatii
42. În metoda Gauss -
a) înmultesc cu pivotul
b) se impart la pivot
c) se aduna cu pivotul
43.. Spectrul unui operator este:
a) o multime de functii
b) multimea valorilor proprii ale operatorului
c) multime de inegrale nedefinite
44. Criteriul lui Raabe - Duhamel este: "Fie seria ![]() si fie
si fie 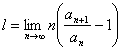
Daca ![]() seria este convergenta
seria este convergenta
Daca ![]() seria este divergenta
seria este divergenta
Daca ![]() nu se poate stabili natura seriei pe baza acestui criteriu"
nu se poate stabili natura seriei pe baza acestui criteriu"
a) incorect
b) corect
c) incomplet
45. 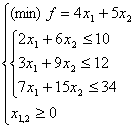 este:
este:
a) 
b) 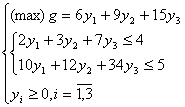
c) 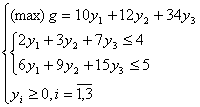
46.. Criteriul de intrare în baza de la algoritmul Simplex este dat de:
a) metoda
Gauss -
b) semnul
diferentelor ![]()
c) vectorul
cu ![]() negative
negative
47.. Punctele lui A care nu sunt puncte de acumulare pentru multimea A se numesc:
a) punct aderent al multimii A
b) punct interior multimii A
c) punct izolat al lui A
48. Operatorul ![]() are matricea corespunzatoare bazelor unitare
are matricea corespunzatoare bazelor unitare ![]() . Sa se calculeze
. Sa se calculeze ![]() unde
unde ![]()
a) 
b) 
c) 
49.Fie aplicatia liniara ![]() Sa se scrie
matricea atasata operatorului f.
Sa se scrie
matricea atasata operatorului f.
a) Matricea
atasata este: ![]()
b) Matricea
atasata este: 
c) Matricea
atasata este: 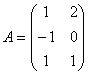
50. Derivata partiala ![]() se calculeaza
considerând:
se calculeaza
considerând:
a) pe y constant si derivând ca o functie de o singura variabila x
b) pe x constant si derivând ca o functie de o singura variabila y
c) x si y constante si folosind regula de derivare pentru produs
51. Operatorul Laplace pentru functia ![]() este:
este:
a) ![]()
b) ![]()
c) ![]()
52. Sa se calculeze integrala: ![]()
a) ![]()
b) ![]()
c) ![]()
53. Sa se integreze ecuatia
diferentiala: ![]() . Solutia generala este:
. Solutia generala este:
a) ![]()
b) ![]()
c) ![]()
54. Sa se calculeze ![]() pentru functia urmatoare:
pentru functia urmatoare: ![]()
a) ![]()
b) ![]()
c) ![]()
55.Derivata partiala ![]() se calculeaza
considerând:
se calculeaza
considerând:
a) pe y constant si derivând ca o functie de o singura variabila x
b) pe x constant si derivând ca o functie de o singura variabila y
c)x si y constante si folosind regula de derivare pentru produs
56. Fie ![]() baza în
baza în ![]() unde:
unde: ![]() Exprimati vectorul
Exprimati vectorul ![]() în aceasta baza.
în aceasta baza.
a) ![]()
b) ![]()
c) ![]()
57. Limita unei functii se calculeaza într-un punct care este:
a) din domeniul de definitie
b) punct de acumulare al domeniului de definitie
c) punct aderent al domeniului de definitie
58. Diferentiala de ordinul I pentru functia ![]() este:
este:
a) ![]()
b) ![]()
c) ![]()
59. Sa se studieze natura seriei 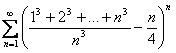
a) Seria este absolut convergenta
b) Seria este divergenta
c) Seria este convergenta
60. În algoritmul Simplex, programul optim se afla din:
a) produsul scalar dintre coeficientii bazici si solutia de baza
b) împartind coloanele la linii
c) înmultind coloanele cu liniile
61. Criteriul necesar de convergenta: "Daca ![]() este o serie convergenta, atunci
este o serie convergenta, atunci ![]() " este:
" este:
a) corect
b) incorect
c) incomplet
62. Formula complementelor este:
a) ![]()
b) ![]()
c) ![]()
63. Criteriul lui Leibnitz: "Fie seria ![]() . Daca sirul
. Daca sirul ![]() este sir descrescator convergent catre zero,
atunci seia este convergenta" este:
este sir descrescator convergent catre zero,
atunci seia este convergenta" este:
a) corect
b) incorect
c) incomplet
64. Sa se integreze ecuatia diferentiala
omogena: ![]()
a) ![]()
b) ![]()
c) ![]()
65. Sa se studieze convergenta integralei: ![]()
a) Integrala este convergenta
b) Integrala este divergenta
c) Integrala este absolut convergenta
66. Forma generala a ecuatiilor liniare de ordinul întâi este:
a) ![]()
b) ![]()
c) ![]()
67. Functia beta are proprietatea:
a) ![]()
![]()
b) ![]()
c)![]()
68. Metoda multiplicatorilor lui Lagrange se aplica functiilor reale de mai multe variabile reale pentru determinarea:
a) punctelor de extrem liber
b) punctelor de extrem conditionat
c) punctelor stationare
69. Criteriul de iesire din baza în algoritmul Simplex este dat de:
a) minimul rapoartelor componentelor solutiei de baza si ale vectorului care intra
b) metoda Gauss-Jordan
c) lema substitutiei
70. Spatiile vectoriale au:
a) acelasi numar de elemente
b) aceleasi tipuri de subspatii
c) aceeasi dimensiune
71. Se numeste functie gama integrala:
a) 
b) 
c) 
72. Vectorii ![]() si
si ![]() se numesc ortogonali daca:
se numesc ortogonali daca:
a) ![]()
b) ![]()
c) ![]()
73. O functie ![]() se numeste
operator liniar daca:
se numeste
operator liniar daca: ![]()
![]()
a) Definitia este corecta
b) Definitia este incorecta
c) Definitia este incompleta
74. Fie în ![]() vectorii
vectorii ![]() liniar independenti. Care este natura sistemului de
vectori
liniar independenti. Care este natura sistemului de
vectori ![]()
a) Vectorii sunt ortogonali
b) Vectorii sunt liniar independenti
c) Vectorii sunt liniar dependenti
75. Sa se studieze natura seriei ![]()
a) Seria este convergenta
b) Seria este absolut convergenta
c) Seria este divergenta
76. Fie ![]() Sa se calculeze:
Sa se calculeze: ![]()
a) ![]()
b) ![]()
c) ![]()
77. Functia ![]() se numeste produs scalar pe multimea
se numeste produs scalar pe multimea ![]() daca:
daca:
1) ![]()
2) ![]()
Definitia este:
a) incorecta
b) incompleta
c) corecta
78. Sa se determine valorile proprii associate
aplicatiei liniare ![]() cu
cu ![]() Valorile proprii sunt:
Valorile proprii sunt:
a) ![]()
b) ![]()
c) ![]()
79. Daca sistemul de vectori ![]() este liniar independent, atunci orice subsistem al sau
este:
este liniar independent, atunci orice subsistem al sau
este:
a) liniar dependent
b) liniar independent
c) sistem de generatori
80. Algoritmul de rezolvare a problemelor de transport are:
a) doua etape
b) trei etape
c) patru etape
81. Ecuatiile diferentiale cu variabile separabile sunt de forma:
a) ![]() cu
cu ![]()
b) ![]() cu
cu ![]()
c) ![]() cu
cu ![]()
82. Unei variabile nenegative din modelul primal îi va corespunde în modelul dual:
a) restrictie egalitate
b) restrictie concordanta
c) restrictie neconcordanta
83. Seria armonica alternata ![]() este:
este:
a) convergenta
b) absolut convergenta
c) divergenta
84. Sa se dezvolte în serie Mac-Laurin functia: ![]()
a) ![]()
b) ![]()
c) ![]()
85. Diferentiala de ordinul II pentru functia ![]() este:
este:
a) ![]()
b) ![]()
c) ![]()
86. Sa se calculeze: ![]() pentru
pentru ![]()
a) ![]()
b) ![]()
c) ![]()
87. Sa se integreze ecuatia: ![]()
a) ![]()
b) ![]()
c) ![]()
88. În forma canonica a unei probleme de maximizare restrictiile sunt:
a) egalitati
b) inegalitati
cu semnul "![]() "
"
c) inegalitati
cu semnul "![]() "
"
89. Stabiliti care afirmatie este falsa:
a) Daca într-o serie se schimba ordinea unui numar finit de termeni atunci nu este influentata nici natura seriei si nici suma seriei în caz de convergenta
b) Daca într-o serie se înlatura un numar finit de termeni atunci natura seriei nu se modifica, ci doar suma ei în caz de convergenta
c) Daca într-o serie se înlatura un numar finit de termini atunci natura seriei nu se modifica si nici suma ei în caz de convergenta
90. Functia C.Cobb - P.Douglas se defineste prin:
a) ![]()
b) ![]()
c) ![]()
91. Se numeste spatiu Euclidian un spatiu pe care s-a definit:
a) o distanta
b) o norma
c) un produs scalar
92. Scalarii ![]() din procedeul de ortogonalizare Gramm - Schmidt se
determina cu formula:
din procedeul de ortogonalizare Gramm - Schmidt se
determina cu formula:
a) ![]()
b) ![]()
c) ![]()
93. Modelarea unei probleme cu continut economic care implica optimizare liniara necesita parcurgerea a:
a) 5 etape
b) 6 etape
c) 3 etape
94. O baza B care verifica relatia: ![]() se numeste:
se numeste:
a) baza primal admisibila
b) baza canonica
c) baza ortogonala
95. Criteriul II al comparatiei: "Fie ![]() si
si ![]() serii cu termini pozitivi si
serii cu termini pozitivi si ![]() . Atunci: 1) Daca
. Atunci: 1) Daca ![]() cele doua serii au aceeasi natura
cele doua serii au aceeasi natura
2)
Daca ![]() si
si ![]() este convergenta
este convergenta ![]()
![]() este convergenta" este:
este convergenta" este:
a) incorect
b) incomplet
c) corect
96. Sa se determine vectorul normat ![]() din
din ![]() ortogonal vectorilor:
ortogonal vectorilor: ![]()
a) ![]()
b) ![]()
c) ![]()
97. Sa se studieze natura seriei: 
a) Seria este absolut convergenta
b) Seria este divergenta
c) Seria este convergenta
98. Se dau vectorii:  . Calculati coordonatele vectorului
. Calculati coordonatele vectorului 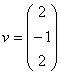 în baza formata din
în baza formata din ![]() si
si ![]() .
.
a) 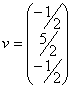
b) 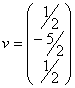
c) 
99. Relatia de legatura dintre functia beta si gama este:
a) ![]()
b) ![]()
c) ![]()
100. Determinati valorile proprii ale operatorului
liniar reprezentat de matricea: 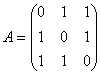
a) Valorile
proprii sunt: ![]()
b) Valorile
proprii sunt: ![]()
c) Valorile
proprii sunt: ![]()
101. Sa se integreze ecuatia
diferentiala: ![]()
a) 
b) ![]()
c) 
102. Sa se verifice care dintre urmatoarele aplicatii sunt transformari liniare (operatori liniari):
1) 
2) ![]()
a) ambele aplicatii sunt operatori liniari
b) T este operator liniar
c) U este operator liniar
103. Diferentiala unei functii ![]() în punctul
în punctul ![]() se va calcula astfel:
se va calcula astfel:
a) ![]()
b) ![]()
c) ![]()
104. Sa se calculeze integrala: 
a) ![]()
b) ![]()
c) ![]()
105. Solutia generala a ecuatiei liniare de ordinul întâi este:
a) ![]()
b) ![]()
c) ![]()
106. Calculati derivatele partiale de ordinul I
pentru functia: ![]()
a) ![]()
b) ![]()
c) ![]()
107. Functia de ![]() variabile reale
variabile reale ![]() are:
are:
a) ![]() derivate partiale de ordinul I
derivate partiale de ordinul I
b) ![]() derivate partiale de ordinul I
derivate partiale de ordinul I
c) ![]() derivate partiale de ordinul I
derivate partiale de ordinul I
108. Fie V un spatiu vectorial n-dimensional peste corpul de
scalari K si ![]() o aplicatie liniara. Un scalar
o aplicatie liniara. Un scalar ![]() se numeste
valoare proprie pentru aplicatia liniara T daca exista cel
putin un vector nul
se numeste
valoare proprie pentru aplicatia liniara T daca exista cel
putin un vector nul ![]() astfel încât
astfel încât ![]() . Definitia este:
. Definitia este:
a) corecta
b) incorecta
c) incompleta
109. Baza ortonormala a unui spatiu Euclidian se construieste din baza ortogonala:
a) împartind fiecare vector al bazei ortogonale la norma sa
b) înmultind fiecare vector al bazei ortogonale cu norma sa
c) adunând fiecare vector al bazei ortogonale cu norma sa
110. Fie F o functie definita pe un domeniu D din ![]() cu valori reale continua în acest domeniu. O
relatie de forma:
cu valori reale continua în acest domeniu. O
relatie de forma: ![]() se numeste:
se numeste:
a) ecuatie cu variabile separabile
b) ecuatie omogena
c) ecuatie diferentiala de ordinul n
111. O problema de programare liniara este în forma canonica daca:
a) toate restrictiile sunt egalitati si toate variabilele sunt nenegative
b) toate restrictiile sunt concordante si toate variabilele sunt nenegative
c) toate restrictiile sunt concordante si toate variabilele sunt negative
112. Spectrul unui operator este:
a) o multime de functii
b) multimea valorilor proprii ale operatorului
c) multime de integrale nedefinite
113. Un sir este marginit daca:
a) elementele de rang par sunt într-un interval
b) elementele sunt într-un interval
c) elementele de rang impar sunt într-un interval
114. Sa se studieze natura seriei ![]()
a) Seria este absolut convergenta
b) Seria este divergenta
c) Seria este convergenta
115. Sa se calculeze produsul scalar al vectorilor: ![]() în
în ![]() .
.
a) ![]()
b) ![]()
c) ![]()
116. Seria Riemann ![]() este:
este:
a) pentru ![]() serie convergenta si pentru
serie convergenta si pentru ![]() serie divergenta
serie divergenta
b) pentru ![]() serie convergenta si pentru
serie convergenta si pentru ![]() serie divergenta
serie divergenta
c) pentru ![]() serie convergenta si pentru
serie convergenta si pentru ![]() serie divergenta
serie divergenta
117. Functia lui Lagrange este:
a) ![]()
b) ![]()
c) ![]()
118. Sa se studieze convergenta integralei ![]()
a) Integrala este divergenta
b) Integrala este convergenta si egala cu 0
c) Integrala este absolut convergenta
119. Determinati valorile proprii ale operatorului liniar
reprezentat de matricea: 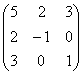
a) Valorile proprii sunt: ![]()
b) Valorile proprii sunt: ![]()
c) Valorile proprii sunt: ![]()
120. Scrieti primii cinci termini ai seriei cu termenul general: ![]()
![]()
a) ![]()
b) ![]()
c) ![]()
121. Calculati derivata partiala de ordinul I
pentru functia: ![]()
a) ![]() ;
; ![]()
b) ![]() ;
; ![]()
c) ![]() ;
; ![]()
122. Fie  . Matricea atasata operatorului este:
. Matricea atasata operatorului este:
a) 
b) 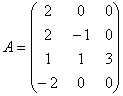
c) 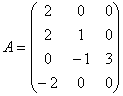
123. Într-un sistem de n vectori liniari independenti conditia de a fi sistem de generatori este înlocuita de relatia:
a) ![]()
b) ![]()
c) ![]()
124. Sa se integreze ecuatia
diferentiala: ![]()
a) ![]()
b) ![]()
c) ![]()
125. Diferentiala de ordinul I a functiei de productie este:
a) ![]()
b) ![]()
c) ![]()
126. Sa se calculeze integrala: 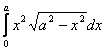
a) ![]()
b) ![]()
c) ![]()
127.Precizati care dintre urmatoarele afirmatii este adevarata:
a) Daca
vectorii ![]() sunt liniar independenti, iar
sunt liniar independenti, iar ![]() sunt liniar dependenti, atunci
sunt liniar dependenti, atunci ![]() este o combinatie
liniara a vectorilor
este o combinatie
liniara a vectorilor ![]() .
.
b) Daca
vectorii ![]() sunt liniar dependenti, iar
sunt liniar dependenti, iar ![]() sunt liniar independenti, atunci
sunt liniar independenti, atunci ![]() este o combinatie
liniara a vectorilor
este o combinatie
liniara a vectorilor ![]() .
.
c) Daca
vectorii ![]() sunt liniar independenti, iar
sunt liniar independenti, iar ![]() sunt tot liniar independenti, atunci
sunt tot liniar independenti, atunci ![]() este o combinatie
liniara a vectorilor
este o combinatie
liniara a vectorilor ![]() .
.
128. Functia: ![]() cu
cu ![]() se numeste:
se numeste:
a) norma a spatiului Euclidian
b) produs scalar a spatiului Euclidian
c) distanta a spatiului Euclidian
129. Daca seria convergenta ![]() are suma
are suma ![]() si seria derivatelor
si seria derivatelor ![]() are suma
are suma ![]() , atunci:
, atunci:
a) ![]()
b) ![]()
c) ![]()
130. Limita unei functii într-un punct exista daca:
a) functia este continua
b) functia este derivabila
c) limitele laterale sunt egale
131. Precizati relatia adevarata:
a) ![]()
b) ![]()
c) ![]()
132. Norma are urmatoarea proprietate:
a) ![]()
b) ![]()
c) ![]()
133. Limita ![]() se numeste:
se numeste:
a) diferentiala de ordinul I a functiei ![]() în raport cu
în raport cu ![]()
b) diferentiala de ordinul n a functiei ![]() în raport cu
în raport cu ![]()
c) derivata partiala a functiei ![]() în raport cu
în raport cu ![]()
134. Sa se calculeze produsul scalar al vectorilor : ![]() în
în ![]()
a) ![]()
b) ![]()
c) ![]()
135. Din trei feluri de materie prima ![]()
![]() disponibile în cantitatile de 28,21 respectiv 10
unitati se preconizeaza a se realiza doua tipuri de produse
disponibile în cantitatile de 28,21 respectiv 10
unitati se preconizeaza a se realiza doua tipuri de produse
![]() care necesita
consumuri specifice de 1,3 respectiv 1unitate pentru
care necesita
consumuri specifice de 1,3 respectiv 1unitate pentru ![]() si 4,1 respectiv 1unitate pentru
si 4,1 respectiv 1unitate pentru ![]() si care aduc un beneficiu pe unitatea de produs de 3
respectiv 4 unitati. Sa se determine planul de productie
care conduce la un beneficiu total maxim.
si care aduc un beneficiu pe unitatea de produs de 3
respectiv 4 unitati. Sa se determine planul de productie
care conduce la un beneficiu total maxim.
Modelul matematic al problemei este:
a) 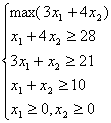
b) 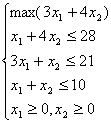
c) 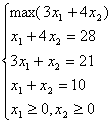
136. Sa se studieze natura seriei: ![]()
a) Seria este absolut convergenta
b) Seria este convergenta
c) Seria este divergenta
137. Fie ![]() baza în
baza în ![]() unde
unde ![]() . Sa se exprime vectorii
. Sa se exprime vectorii ![]() în aceasta baza.
în aceasta baza.
a) 
b) 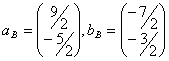
c) 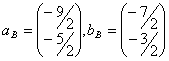
138. Sa se calculeze derivatele partiale de ordinul I pentru
functia 
a) ![]()
b) ![]()
c) ![]()
139. Criteriul raportului al lui D'Alembert: "Fie seria ![]() si fie
si fie ![]()
Daca ![]() seria este convergenta
seria este convergenta
Daca ![]() seria este divergenta
seria este divergenta
Daca ![]() nu se poate stabili natura seriei pe baza acestui criteriu"
este:
nu se poate stabili natura seriei pe baza acestui criteriu"
este:
a) incorect
b) corect
c) incomplet
140. Operatorul Laplace este:
a) operator de derivate partiale de ordin I
b) operator de derivate partiale de ordin II
c) operator de derivate partiale de ordin III
141. Diferentiala functiei ![]() este:
este:
a) ![]()
b) ![]()
c) ![]()
142. Care este valoarea integralei Euler - Poisson 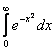 ?
?
a) 
b) 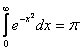
c) 
143. Sa se studieze natura seriei: ![]()
a) Seria este divergenta
b) Seria este convergenta
c) Seria este absolut convergenta
144. Sa se calculeze integrala 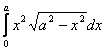
a) ![]()
b) ![]()
c) ![]()
145. Relatia de recurenta a functiei ![]() este:
este:
a) ![]()
b) ![]()
c) ![]()
146. Diferentiala de ordinul II pentru functia ![]() este:
este:
a) ![]()
b) ![]()
c) ![]()
147. Sa se calculeze: ![]() unde
unde ![]()
a) ![]()
b) ![]()
c) ![]()
148. Fie ![]() si
si ![]() . Punctul
. Punctul ![]() este un punct de maxim local daca
este un punct de maxim local daca ![]() . Definitia este:
. Definitia este:
a) corecta
b) incorecta
c) incompleta
149. Norma are urmatoarea proprietate:
a) ![]()
b) ![]()
c) ![]()
150. O solutie de baza a unei probleme de transport are un numar de componente nenule egale cel mult cu:
a) ![]()
b) ![]()
c) ![]()
151. Fie seria ![]() convergenta cu
convergenta cu ![]() atunci seria integralelor termenilor
atunci seria integralelor termenilor ![]() este o serie:
este o serie:
a) convergenta pe ![]()
b) absolut convergenta pe ![]()
c) divergenta pe ![]()
152. Stabiliti care afirmatie este adevarata:
a) Orice punct stationar este punct de extrem pentru functie
b) Nu orice punct stationar este punct de extrem pentru functie
c) Orice punct stationar este punct de minim pentru functie
153. Unei restrictii neconcordante din modelul primal îi corespunde în modelul dual:
a) variabila nenegativa
b) variabila nepozitiva
c) variabila libera
154. Sa se studieze natura seriei 
a) Seria este divergenta
b) Seria este absolut convergenta
c) Seria este convergenta
155. Se considera functia: ![]() Se cere sa se calculeze:
Se cere sa se calculeze: ![]()
a) ![]()
b) ![]()
c) ![]()
156. Fie ![]() un operator liniar care are matricea corespunzatoare
bazelor canonice
un operator liniar care are matricea corespunzatoare
bazelor canonice ![]() Sa se determine valorile proprii ale lui U.
Sa se determine valorile proprii ale lui U.
a) ![]()
b) ![]()
c) ![]()
157. Orice problema de transport are întotdeauna o solutie admisibila de forma:
a) ![]() unde
unde ![]()
b) ![]() unde
unde ![]()
c) ![]() unde
unde ![]()
158. O baza care conduce la un program optim se numeste:
a) baza admisibila
b) baza ortogonala
c) baza ortonormala
159. Fie seria ![]() Daca sirul sumelor partiale
Daca sirul sumelor partiale ![]() este:
este:
a) un sir monoton
b) un sir monoton si marginit
c) un sir marginit
atunci seria este convergenta.
160. Sa se determine punctele de extrem ale functiei: ![]()
a) ![]() este punct de minim si
este punct de minim si ![]() nu este punct de extrem
nu este punct de extrem
b) ![]() este punct de minim si
este punct de minim si ![]() este punct de maxim
este punct de maxim
c) ![]() nu este punct de extrem si
nu este punct de extrem si ![]() punct de minim
punct de minim
161. Sa se calculeze integrala: ![]()
a) ![]()
b) ![]()
c) ![]()
162. Produsul scalar este:
a) o functionala biliniara pozitiv definita
b) o functionala biliniara negativ definita
c) o functionala biliniara semipozitiv definita
163. În orice spatiu Euclidian ![]() - dimensional peste corpul K exista cel putin o
baza ortogonala ce se poate determina:
- dimensional peste corpul K exista cel putin o
baza ortogonala ce se poate determina:
a) cu procedeul Gramm - Schmidt
b) cu procedeul Gauss - Jordan
c) cu criteriul Raabe - Duhamel
164. Fie 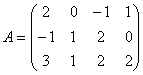 si fie
si fie ![]() vectorii coloana
din A. Care afirmatie este adevarata?
vectorii coloana
din A. Care afirmatie este adevarata?
a) ![]() formeaza baza în
formeaza baza în ![]()
b) ![]() nu formeaza baza în
nu formeaza baza în ![]()
c) ![]() formeaza
baza în
formeaza
baza în ![]()
165. Sa
se studieze convergenta integralei: ![]()
d) Integrala este convergenta
e) Integrala este divergenta
f) Integrala este absolut convergenta
166. Forma generala a ecuatiilor liniare de ordinul întâi este:
a) ![]()
b) ![]()
c) ![]()
167. Functia beta are proprietatea:
a)![]()
![]()
b)![]()
c) ![]()
168. În programul optim necunoscutele secundare se completeaza cu:
a) elemente negative
b) zerouri
c) elemente positive
169. Valorile proprii ale unui operator sunt solutii:
a) ale unei ecuatii de gr.2
b) ale unei ecuatii diferentiale
c) ale ecuatiei ![]()
170. Criteriul II al comparatiei este: "Fie ![]() si
si ![]() serii cu termini pozitivi si
serii cu termini pozitivi si ![]() . Atunci:
. Atunci:
I.
Daca ![]() cele doua serii au aceeasi natura
cele doua serii au aceeasi natura
II.
Daca ![]() si
si ![]() este divergenta
este divergenta ![]()
![]() este divergenta" este:
este divergenta" este:
a) incorect
b) incomplet
c) corect
171.În metoda Gauss - Jordan elementele se calculeaza cu:
a) regula dreptunghiului
b) regula lui Sarrus
c) regula triunghiului
172. Teorema ecarturilor complementare este:
O conditie
necesara si suficienta ca un cuplu de solutii admisibile de
baza ![]() si
si ![]() sa fie optim este
ca solutiile sa verifice simultan relatiile:
sa fie optim este
ca solutiile sa verifice simultan relatiile:
a) 
b) 
c) 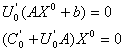
173. Criteriul lui Raabe - Duhamel este: "Fie seria ![]() si fie
si fie 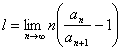 .
.
Daca ![]() seria este divergenta
seria este divergenta
Daca ![]() seria este convergenta
seria este convergenta
Daca ![]() nu se poate stabili natura seriei pe baza acestui criteriu"
nu se poate stabili natura seriei pe baza acestui criteriu"
a) incorect
b) incomplet
c) corect
174. Fie operatorii liniari: 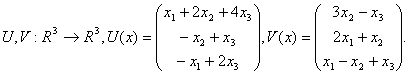 Daca A,B,C sunt
matricile lui
Daca A,B,C sunt
matricile lui ![]() corespunzatoare bazelor canonice, ce legatura
exista între A,B si C?
corespunzatoare bazelor canonice, ce legatura
exista între A,B si C?
a) ![]()
b) ![]()
c) ![]()
175. Sa se determine valorile proprii pentru matricea: ![]() Valorile proprii sunt:
Valorile proprii sunt:
a) ![]()
b) ![]()
c) ![]()
176. O întreprindere urmareste maximizarea
beneficiului în întocmirea planului de productie la 3 produse ![]() din doua materii prime
din doua materii prime ![]() si
si ![]() cu un disponibil de 60 respectiv 50 unitati.
Coeficientii tehnologici pentru aceste materii prime sunt dati în
tabelul de mai jos:
cu un disponibil de 60 respectiv 50 unitati.
Coeficientii tehnologici pentru aceste materii prime sunt dati în
tabelul de mai jos:
|
|
|
|
|
|
|
4 |
1 |
2 |
|
|
1 |
2 |
1 |
Planul de productie la ![]() si
si ![]() nu trebuie sa fie mai mare de 40 u. Beneficiile unitare
aduse de
nu trebuie sa fie mai mare de 40 u. Beneficiile unitare
aduse de ![]() sunt de 18,20 si
respective 15 u. se cere sa se construiasca modelul matematic.
sunt de 18,20 si
respective 15 u. se cere sa se construiasca modelul matematic.
Modelul matematic este:
a) 
b) 
c) 
177. Stabiliti natura seriei de termen general: 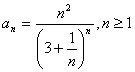
a) Seria este semiconvergenta
b) Seria este convergenta
c) Seria este divergenta
178. Numarul ![]() , raza de convergenta a unei serii de puteri, se
poate determina daca exista urmatoarele limite:
, raza de convergenta a unei serii de puteri, se
poate determina daca exista urmatoarele limite:
a) 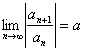 sau
sau ![]()
b) 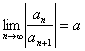 sau
sau ![]()
c) 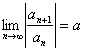 sau
sau ![]()
179. Vectorii  din
din ![]() formeaza o
baza în
formeaza o
baza în ![]() daca si
numai daca determinantul matricei
daca si
numai daca determinantul matricei 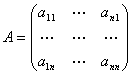 formata cu cei n
vectori este:
formata cu cei n
vectori este:
a) nul
b) nenul
c) pozitiv
180. Ecuatia: ![]() este:
este:
a) o ecuatie diferentiala omogena
b) o ecuatie diferentiala cu variabile separabile
c) o ecuatie diferentiala de ordinul I liniara
181. Se dau vectorii:  Se cere sa se construiasca o baza
ortogonala a spatiului Euclidian
Se cere sa se construiasca o baza
ortogonala a spatiului Euclidian ![]() .
.
a) 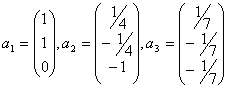
b) 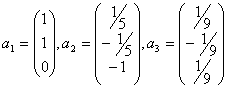
c) 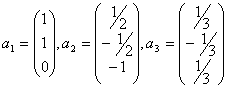
182. Se considera functia: ![]() Se cere sa se calculeze
Se cere sa se calculeze ![]()
a) ![]()
b) ![]()
c) ![]()
183.Metoda multiplicatorilor lui Lagrange se aplica functiilor reale de mai multe variabile reale pentru determinarea:
a) punctelor de extrem liber
b) punctelor stationare
c) punctelor de extrem conditionat
184. Sa se integreze ecuatia
diferentiala: ![]()
a) 
b) 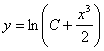
c) 
185. Utilizând functiile gama si beta sa se
calculeze integrala: 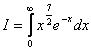
a) ![]()
b) ![]()
c) ![]()
186. Sa se stabileasca natura urmatoarei
integrale improprii: 
a) divergenta
b) convergenta
c) absolut convergenta
187. Sa se determine extremele functiei: ![]() , variabilele fiind legate prin conditia
, variabilele fiind legate prin conditia ![]()
a) punctul ![]() este punct de minim conditionat pentru
este punct de minim conditionat pentru ![]()
b) punctul ![]() este punct de minim conditionat pentru
este punct de minim conditionat pentru ![]()
d) punctul
![]() este punct de minim conditionat pentru
este punct de minim conditionat pentru
188. Spectrul unui operator este:
a) o multime de functii
b) multimea valorilor proprii ale operatorului
c) multime de integrale nedefinite
189. Matricea hessiana pentru o functie reala de n variabile reale contine derivate partiale:
a) de ordinul unu
b) de ordinul doi
c) de ordinul n
190. Se numeste functie gama integrala:
a) 
b) 
c) 
191 Criteriul de iesire din baza în algoritmul Simplex este dat de:
a) minimul rapoartelor componentelor solutiei de baza si ale vectorului care intra
b) metoda Gauss - Jordan
c) lema substitutiei
192. Fie seria ![]() Daca sirul sumelor partiale
Daca sirul sumelor partiale ![]() este:
este:
a) un sir nemarginit
b) un sir monoton si marginit
c) un sir strict crescator
atunci seria este convergenta
193. O baza a spatiului Euclidian se numeste ortonormala daca:
a) este o baza ortogonala si norma
fiecarui vector este ![]()
b) este o baza ortogonala si norma
fiecarui vector este ![]()
c) este o baza ortogonala si norma
fiecarui vector este ![]()
194. Fie operatorul
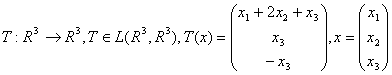 . Scrieti ecuatia caracteristica a
operatorului T.
. Scrieti ecuatia caracteristica a
operatorului T.
a) 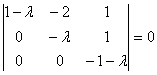
b) 
c) 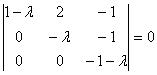
195. Sa se calculeze produsul scalar al vectorilor: ![]() si
si ![]() în
în ![]() .
.
a) ![]()
b) ![]()
c) ![]()
196. Sa se studieze natura seriei: ![]() . Seria este:
. Seria este:
a) divergenta
b) absolut convergenta
c) convergenta
197. Limita unei functii într-un punct exista daca:
a) functia este continua
b) functia este derivabila
c) limitele laterale sunt egale
198. Fie urmatoarele sisteme de vectori:

 . Fie
. Fie 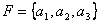 si
si ![]() Care afirmatie este adevarata?
Care afirmatie este adevarata?
a) F
este baza în ![]() si G nu este baza în
si G nu este baza în ![]()
b) F
si G sunt baze în ![]()
c) F
nu este baza în ![]() si G este
baza în
si G este
baza în ![]()
198. Sa se calculeze derivatele partiale de ordinul I pentru functia urmatoare:
![]()
a) ![]()
b) ![]()
c) ![]()
199. Ecuatia diferentiala: ![]() este:
este:
a) ecuatie diferentiala cu variabile separabile
b) ecuatie diferentiala omogena
c) ecuatie diferentiala de ordinul I liniara
200. Pentru a determina natura seriei: 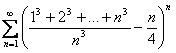 vom aplica:
vom aplica:
a) Criteriul radacinii al lui Cauchy
b) Criteriul raportului al lui D'Alembert
c) Criteriul lui Raabe - Duhamel
|