Metode de rezolvare a problemelor de constructii geometrice

METODE DE REZOLVARE A PROBLEMELOR DE CONSTRUCTII GEOMETRICE

Constructiile geometrice se fac cu ajutorul unor instrumente geometrice, dintre care  cele mai importante sunt rigla si compasul.Rigla serveste la construirea dreptelor, iar compasul la masurarea segmentelor congruente cu un segment dat si la construirea cercului.

Problemele de constructie sunt acele probleme de geometrie in care se cere sa se construiasca o anumita figura, cu ajutorul unor elemente date, sau construirea unei figuri in asa fel incat elementele ce o compun sa aiba anumite proprietati, folosind numai rigla si compasul.

Rezolvarea problemelor prin constructii geometrice ofera certitudinea ca din moment ce o figura a putut fi construita pe baza datelor, inseamna ca ea este determinata, masurile rezultate in figura trebuie sa rezulte si din calcule.Dintre toate problemele de geometrie, problemele de constructii geometrice sunt acelea care stimuleaza in cel mai inalt grad spiritul de observatie, claritatea gandirii si logica rezolvitorilor.

Caracteristica constructiilor geometrice consta in faptul ca exactitatea fiecarei constructii trebuie motivata logic iar posibilitatea executarii ei , cu instrumentele indicate, trebuie sa fie demonstrata.

Problemele de constructie pot fi privite ca o aplicare practica a cunostintelor de geometrie.

Cu rigla si compasul pot fi facute urmatoarele constructii simple:

constructia unui segment de dreapta ce trece prin doua puncte date.

determinarea punctului de intersectie a doua drepte date

constructia unui cerc, cu centrul si raza date

determinarea punctelor de intersectie dintre o dreapta data si un cerc dat

determinarea punctelor de intersectie a doua cercuri

Spunem ca o problema de constructie este rezolvabila cu rigla si compasul, daca pentru solutionarea ei este necesar un numar finit de constructii de tipul 1-5.

Rezolvarea unei probleme de constructie consta nu atat in construirea figurii, cat in raspunsul la intrebarea cum sa executam aceasta constructie, precum si in demonstratia respectiva.Dificultatea in rezolvarea problemelor de constructie consta in a gasi ordinea in care se succed elementele de constructie.

Problema se considera rezolvata daca este indicat procedeul de constructie a figurii si este demonstrat ca, in urma executarii constructiilor indicate, se obtine , intr-adevar, figura cu proprietatile cerute.Unele probleme de constructii geometrice sunt aplicarea directa a unor proprietati ale figurilor, sau a unor teoreme de geometrie (de exemplu, construirea , printr-un punct exterior unei drepte a unei paralele la acea dreapta). Alteori, insa, problemele nu mai sunt asa de simple. 838i82i

In scoala, ( gimnaziu sau liceu ),pentru rezolvarea unor astfel de probleme sunt folosite:

metoda substitutiilor succesive

metoda intersectarii locurilor geometrice

metoda figurilor asemenea

metoda transformarilor geometrice

alte metode

1. METODA SUBSTITUTIILOR SUCCESIVE

Aceasta metoda consta in a reduce problema data la o alta problema, apoi pe aceasta la o a treia, si asa mai departe, pana cand ajungem la o problema cunoscuta sau care are o rezolvare imediata. Metoda substitutiilor succesive reprezinta de fapt calea cea mai naturala de a demonstra o afirmatie a carei veridicitate nu este imediata.

Totusi, in acest lant de propozitii trebuie sa tinem seama de urmatorul fapt: problema data A o reducem la B, apoi la C, pana la propozitia finala Z, care este evidenta sau care a fost deja demonstrata.

Pentru exactitatea rationamentului insa, este necesar sa ne asiguram de echivalenta a doua propozitii consecutive din acest lant. Cu alte cuvinte, fiecare propozitie trebuie sa o implice pe cea anterioara, in caz contrar, putandu-se intampla ca ultima propozitie sa nu o implice pe prima.

Uneori, problema la care reducem o problema data este mai generala ca prima.Atunci va trebui sa ne asiguram ca printre solutiile problemei a doua nu introducem pe acelea care nu corespund problemei initiale.

Problema 4. 1.1. Construiti un triunghi cunoscand a,b si m_c.

Demonstratie: (fig. 4.1.1.) Construim,in mod arbitrar, [CE] cu CE=m_c. deoarece sunt cunoscute lungimile laturilor a si b, rezulta ca putem construi cu centrul in C cercurile de raze a, respectiv b. Problema se reduce, in acest moment,la urmatoarea :

,, Fiind date cercurile C₁(O₁,R₁) si C₂(O₂, R₂), precum si punctul fixat M, construiti o dreapta d care trece prin M cu proprietatea ca exista AI d C₁ si B I d C₂, astfel incat M este mijlocul lui [AB]. ’’

Pentru a rezolva aceasta problema, o presupunem rezolvata. Consideram O’₂ simetricul lui O₂ fata de M. Cum [OM₂]s[ M O’₂] si [MA]s[ MB] T D MAO’₂ s D MBO₂, de unde O’₂A= O₂B=R₂ ; asadar, daca C’₂ este cercul cu centrul in O’₂, de raza R₂, avem ca

AI C’₂ C_1. Observam ca A I C’₂ C₁ B I C₂ C₁

Constructia: Se construieste simetricul cercului C₂(O₂, R₂) ( fata de punctul M), cercul

C’₂( O’₂, R₂). Avem mai multe cazuri :

C₁ C₂’= . Problema nu are solutii in acest caz.

C₁ C₂’= (cercurile sunt tangente). Problema are, in acest caz, o singura solutie, anume dreapta MA.

C₁ C₂’= ( cercurile sunt secante). Problema are in acest caz doua solutii, anume dreptele MA₁ si MA₂.

Revenind la constructia initiala, nu avem decat sa aplicam rezultatul de mai sus, facand M=E, O₁=O₂=C, R₁=a, R₂=b.

Fig. 4.1.1.

Problema 4.1.2. Intr-un cerc dat, inscrieti un patrulater, cunoscand doua laturi opuse si suma celorlalte doua laturi opuse.

Demonstratie: (fig. 4.1.2.)

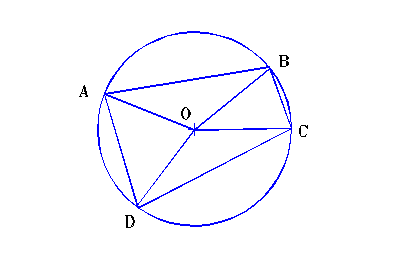Fig. 4.1.2.

Presupunem problema rezolvata. Fie ABCD patrulaterul cautat si presupunem ca laturile [AD] si [BC] sunt cunoscute, ca si suma AB+CD. Cunoscand AD si BC, stim de fapt unghiurile AOD si BOC ceea ce ne permite sa spunem ca : m(< AOB) + m(< COD) = 360 ⁰ – m(< AOD) –m(< BOC) . ( pentru a avea sens aceste calcule, in orice situatie, prin m(<AOD) vom desemna masura arcului care nu contine punctele B si C, deci pot apare si masuri de unghiuri mai mari ca 180⁰).Cele de mai sus ne arata ca de fapt problema se reduce la urmatoarea:,,Fiind dat un arc de cerc cu capetele in M si N gasiti un punct pe acest arc de cerc astfel incat MP+PN=l,fiind lungimea data.’’

Fie P₁ un punct oarecare pe acest arc de cerc ( fig. 4.1.2.a) , atunci α = < MP₁N este acelasi pentru orice punct P₁ ales pe arcul de cerc. Prelungim segmentul [NP₁] cu un segment [P₁T] s [P₁M]. Avem : MP₁+ P₁N = NP₁ + P₁T= NT si cum D MP₁T-isoscel, rezulta ca m(< MTN) =m( <MP₁N), deci,atunci cand P₁ parcurge arcul dat capabil de unghiul α , T se misca pe arcul capabil de unghiul cu capetele in M si N. Constructia este evidenta. Se construieste de aceeasi parte a arcului dat arcul capabil de unghi .Se intersecteaza acest arc cu cercul de centru N si raza l. Se obtin doua puncte, un punct, sau niciunul.

Fig. 4.1.2 a

Pentru T punctul de intersectie, gasim punctul P cautat la intersectia dreptei NT cu arcul dat. Problema poate avea doua solutii, o solutie sau niciuna.

Efectuam acum constructia ceruta in problema initiala.Consideram pe cercul dat doua puncte M si N astfel incat arcul are masura 360-m- m.Determinam acum P pe arcul astfel incat MP+PN sa aiba valoarea data in enunt pentru suma a doua laturi opue in patrulater, folosind constructia expusa mai devreme.Putem gasi doua solutii, una sau niciuna.

Pentru fiecare pereche de segmente ( MP), (PN) obtinuta rezulta cate doua solutii la problema data punand MP=AB, PN=CD sau MP=CD, PN=AB, constructia fiind imediata, pornindu-se dintr-un punct arbitrar A al cercului si gasind succesiv punctele B, C, D folosind lungimile cunoscute AB, BC, respectiv CD. Din modul cum am gasit AB si CD, latura (AD) obtinuta va corespunde cu valoarea din enunt.

Problema 4.1.3. Trasati intr-un cerc dat o corda de lungime si directie date.

Demonstratie (fig. 4.1.3.).

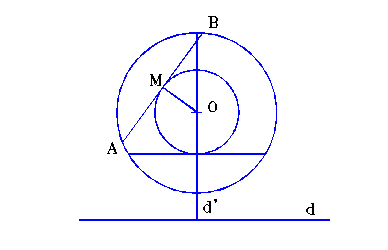Fig. 4.1.3.

Fie C cercul dat, cu centrul in O si d directia cunoscuta. Notam cu l lungimea corzii cautate. Consideram in cercul C o coarda [AB] arbitrara de lungime l.Fie OM AB, M I AB.

Avem OM = , R-raza cercului dat. Evident, problema s-a redus la constructia unei tangente paralele cu dreapta d la cercul cu centrul in O si de raza OM=.

Pentru a efectua aceasta, consideram d’ d, O I d’ si = d’ C

Solutiile cautate se obtin ducand prin P si Q paralele la dreapta d. In concluzie avem urmatoarele cazuri :

1) . Problema nu are solutie.

2) = R. Problema are o solutie si anume, diametrul paralel cu dreapta d

3 ) < R. problema are cele doua solutii considerate mai sus.

2. METODA INTERSECTARII LOCURILOR GEOMETRICE

O mare parte a problemelor de geometrie se rezuma in esenta la a determina un punct care satisface anumite conditii. Metoda locurilor geometrice, datorita scolii lui Platon, consta in esenta in urmatoarele:

Fie P un punct care trebuie sa satisfaca conditiile c₁, c₂ , c₃ ,….,c_n.Consideram L_i LG al punctelor din plan care satisfac conditia c_i , cu i= 1,2,…,n. Multimea punctelor P, solutii ale problemei initiale, este intersectia multimilor L₁, L₂ , …, L_n. Intr-adevar, daca punctul P satisface toate conditiile c₁, c₂ , c₃ ,….,c_n , atunci punctul P apartine tuturor multimilor L₁, L₂ , …, L_n, deci si intersectiei lor. Reciproc, daca punctul P apartine intersectiei multimilor L₁, L₂ , …, L_n,atunci apartine tuturor multimilor, deci satisface toate conditiile c₁, c₂ , c₃ ,….,c_n.

Sa observam ca in general o astfel de problema poate sa nu aiba solutie unica, deoarece intersectia multimilor L₁, L₂ , …, L_n poate sa nu fie formata dintr-un singur punct.

Eleganta si valoarea practica a solutiei unei astfel de probleme depinde in mod esential de alegerea conditiilor c₁, c₂ , c₃ ,….,c_n.

Aceasta metoda poate fi folosita cu succes atat la rezolvarea cat si la discutiile unei probleme: numarul de solutii al problemei este egal cu numarul de puncte din intersectia multimilor L₁, L₂ , …, L_n .

Exemplul 1: Pentru a gasi centrul unui cerc care trece prin trei puncte distincte A, B, C date, procedam astfel : consideram O acest centru; atunci OA= OB si OB=OC. Alegem deci conditiile:

c₁) OA= OB

c₂) OB= OC.. In acest caz L₁ este mediatoarea lui [AB], d₁, iar L₂ este mediatoarea lui [BC], d₂.Deci punctul O se obtine din intersectia dreptelor d₁ si d₂ . Sa urmarim in ce conditii aceasta intersectia este vida.

d₁ d₂= este echivalent cu d₁|| d₂.

Dar d₁ AB si d₂ BC, rezulta A, B, C coliniare si distincte. Daca A,B,C nu sunt coliniare, atunci d₁ si d₂ nu sunt paralele si cum nu coincid, rezulta ca ele vor avea un punct de intersectie unic. Deci pentru cele trei puncte A,B,C necoliniare, exista un unic punct egal departat de toate trei.

Exemplul 2: Fie A un punct exterior unui cerc de centru O. Construiti tangenta din A la acest cerc

Aceasta tangenta este complet determinata de doua puncte.Unul din puncte este A, deci mai trebuie sa determinam inca un punct de pe aceasta tangenta. Cel mai simplu este sa determinam punctul de tangenta T.

Iata cum problema noastra care cerea determinarea unei drepte s-a redus la a determina un punct. Pentru acest punct avem OT AT. Alegem conditiile:

c₁) T se afla pe cerc, cu locul corespunzator , L₁, cercul dat si

c₂) AT OT, cu locul corespunzator L₂, cercul de diametru [OA].Atunci punctul T se obtine din intersectia acestor doua cercuri. Deoarece al doilea cerc contine un punct A exterior si un punct O interior primului cerc, cele doua cercuri vor fi secante si vor avea exact doua puncte de intersectie.Prin urmare, problema are exact doua solutii si anume cele doua puncte de intersectie ale cercurilor.

Problema 4.2.1. Fie trei drepte paralele date a,b,c si A₀B₀C₀ un triunghi ascutitunghic dat. Construiti un triunghi asemenea cu triunghiul A₀B₀C₀ astfel incat A sa apartina dreptei a, B dreptei b si C dreptei c.

Demonstratie : (fig. 4.2.1.) Consideram problema rezolvata.

Fie B un punct oarecare pe dreapta situata intre celelalte doua, M proiectia punctului B pe dreapta a si A’ un punct pe dreapta a astfel incat < BA’M s < C₀ A₀B₀ Unim C cu A’. Atunci patrulaterul BA’AC va fi inscriptibil, deci < CA’B s < CAB, adica cu < C₀ A₀B_0.

Fig. 4.2.1.

Fixand punctul B si punctul A’ va fi fixat, deci C se va afla la intersectia dintre c si o semidreapta cu originea in A’ care formeaza cu A’B un unghi congruent cu < C₀ A₀B_0.. Punctul A se obtine intersectand dreapta a cu o semidreapta de origine B si care formeaza cu BC (determinat) un unghi congruent cu < C₀ A₀B_0..

Problema 4.2.2. Construiti un cerc de raza data, care trece printr-un punct dat P si intersecteaza o dreapta d dupa o coarda de lungime data.

Demonstratie: Neglijand conditia ca cercul sa treaca prin punctul dat, reducem problema la una de loc geometric: ,, Gasiti locul geometric al centrelor cercurilor cu raza fixata R si care intersecteaza o dreapta d dupa o coarda de lungime fixata a’’.

Fie C( O, R ) astfel incat C d = cu AB = a  (fig. 4.2.2.)

Fig.4.2.2.

Daca M este proiectia lui O pe d, rezulta OM= - fixata, ceea ce ne arata ca

O d₁ d₂, d₁ si d₂ fiind cele doua drepte paralele cu d aflate la distanta . Reciproc avem in mod evident ca orice cerc cu centrul in d₁ d₂ de raza R intersecteaza pe d dupa un segment de lungime a.

Concluzionand avem :

1) > R. LG este multimea vida

2) =R. LG este chiar dreapta d.

3) < R. LG este d₁ d_2, unde d₁|| d₂|| d si d₁ si d₂ sunt simetrice fata de d la distanta de d.

Revenim la problema de constructie. Observam ca pentru R, dreptele care dau LG pot fi construite. Solutia problemei de constructie va fi data de intersectia LG de mai sus cu cercul de centru P si raza R

Problema 4.2.3. Fiind date doua puncte A si B construiti un punct C pe o dreapta data ( sau un cerc dat) cu proprietatea ca raportul distantelor sale la punctele A si B au o valoare data k; k>0

Demonstratie: In mod evident problema este echivalenta cu construirea LG al punctelor C cu proprietatea si intersectam deci cu dreapta sau cu cercul dat. Vom rezolva deci urmatoarea problema. ,, Gasiti LG al punctelor C cu proprietatea ca > 0’’.

In cazul in care k=1, in mod evident LG este mediatoarea segmentului [AB].

In continuare putem presupune fara a restrange generalitatea k>1, altfel schimbam A si B intre ele. Construim (fig. 4.2.3) un punct C astfel incat .Fie M si N punctele de intersectie ale bisectoarelor interioara, respectiv exterioara unghiului <ACB cu dreapta AB. Din teorema bisectoarei obtinem 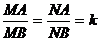, asadar punctele M si N sunt fixate pe AB. Deoarece k>1 avem M I [AB] si NI(AB. Cum < MCN este drept, afirmam ca LG cautat este cercul de diametru [MN].

Fig.4.2.3.

Reciproc fie C un punct oarecare pe cerc. Demonstram intr-adevar : =k. Daca C=M sau C=N, evident. Presupunem ca C este pe cercul de diametru [MN], C N. Fie O mijlocul lui [MN].Relatia : k=, se poate scrie folosind MA = OA - OM, MB = OM – OB,

NA = OA + ON = OA + OM si NB = ON + OM = OM + OB . Este foarte importanta observatia : O este in afara lui (AB); daca presupunem O I (BM) si facand ca mai sus obtinem: MA = OA – OM , MB = OM + OB, NA = OA + OM, NB = OM- OB si dupa calcule : , contradictie).

Facand calculele obtinem : adica .Dar ( OM ) s ( OC ) T deci D OCB D OAC, de unde < OCB s < BAC.

Dar din proprietatile triunghiului dreptunghic avem ca : [OC] s [OM], deci < OCM s < OMC.

Putem scrie : m( < OCB) +m(<BCM)=m(<OCM) = m(<MCA) +m(< BAC).Din prima si ultima relatie, obtinem < BCM s < ACM, deci [ CM este bisectoarea < BAC. Conform teoremei bisectoarei , ceea ce incheie demonstratia.

Asadar pentru a efectua constructia ( in cazul k 1) nu avem decat sa construim cercul de diametru [MN], M si N puncte cunoscute, si sa-l intersectam cu cercul sau dreapta data.

Problema 4.2.4 Construiti un patrulater inscriptibil cunoscandu-i laturile.

Demonstratie : Presupunem problema rezolvata. Alegem M pe dreapta CD astfel incat D este intre M si C si < MAD s < CAB ( fig. 4.2.4), lucru totdeauna posibil deoarece m(<MAD) > >m(< CAB)).

Patrulaterul ABCD este inscriptibil, deci < ABC s < ADMT D AMD D ACB T Raportul fiind cunoscut T este si el cunoscut, precum si lungimea .

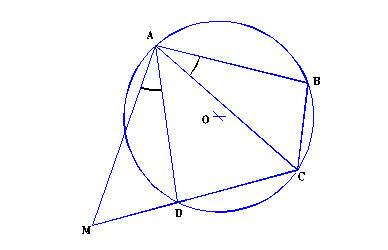Fig. 4.2.4.

Cu datele din enunt avem ca punctele M,D,C sunt date, lungimea AD este cunoscuta precum si raportul . Gasirea punctului A se reduce la constructia unui punct ( chiar A) care se afla pe cercul D si raza data si care are raportul distantelor de la M si C cunoscut.Dar aceasta este chiar problema anterioara .

Presupunand D AMC construit , totul decurge in mod natural, punctul B fiind gasit usor, deoarece se cunosc laturile [AB] , [BC] ( intersectia C(A,AB) cu C(C,BC)).Consideratiile de mai sus ne asigura ca patrulaterul ABCD este inscriptibil ( < ADM s <ABC, ptr. ca D AMD D ACB).

3. METODA TRANSFORMARILOR GEOMETRICE

Un loc central in studiul proprietatilor geometrice ale figurilor plane il ocupa transformarile geometrice. In acest paragraf este pus in evidenta rolul important pe care-l au transformarile geometrice la rezolvarea unor probleme de constructii geometrice.Sunt prezentate probleme de constructii geometrice la a caror rezolvare folosim translatia, simetria centrala, simetria axiala, rotatia, omotetia si inversiunea.

Problema 4.3.1. Fie C(O₁, r₁), C(O₂,r₂) doua cercuri si d o dreapta oarecare. Construiti o dreapta paralela cu d, astfel incat intersectand-o cu cercurile C(O₁,r₁) si C(O₂,r₂) sa obtinem coarde congruente.

Demonstratie: (fig. 4.3.1.) Fie A=pr_dO₂, O’₁= .Translatam cercul C(O₁,r₁) paralel cu dreapta d, astfel incat noul cerc sa aiba centrul in O’₁si raza r₁.

Fie =C(O₂, r₂) C(O’₁, r₁) dreapta BC este cea cautata.

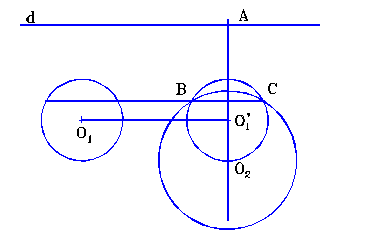Fig. 4.3.1.

Problema 4.3.2. Construiti un trapez cunoscand lungimile laturilor lui.

Demonstratie: ( fig. 4.3.2). fie a,b,c ,d lungimile laturilor unui trapez, astfel incat a si c sunt lungimile bazelor trapezului ( a>c), iar b si d sunt lungimile laturilor neparalele. Se construieste triunghiul avand ca lungimi ale laturilor a-c, b si d, apoi se translateaza latura de lungime b ( sau de lungime d) pe directia corespunzatoare dreptei pe care se afla segmentul a-c cu un vector de lungime c .

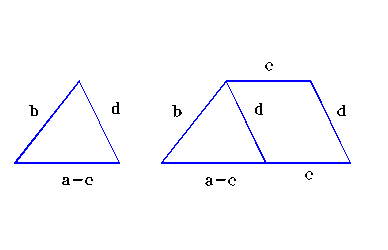Fig. 4.3.2

Problema 4.3.3 Se considera un triunghi echilateral ABC si fie M un punct oarecare

in plan ce nu apartine cercului circumscris triunghiului. Sa se arate ca,cu segmentele [MA] , [MB], [MC] se poate construi un triunghi.

Demonstratie: ( 4.3.3) Consideram rotatia de centru A si unghi α= 60⁰ care duce punctul B in C. Prin aceasta rotatie, punctul M merge in M’, astfel incat AM = AM’si m( < MAM’)=60⁰T AM=AM’. Segmentul [MB} merge in segmentul [M’C], deci MB=M’C. Este usor de vazut ca laturile triunghiului M’MC sunt [MM’]s [MA], [M’C]s [MB] si [MC].

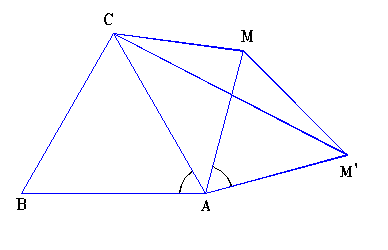Fig. 4.3.3.

Observatie.daca MI cercului circumscris triunghiului echilateral ABC, atunci cel mai mare

din segmentele [MA], [MB], [MC] are lungimea egala cu suma lungimilor celorlalte doua.

Problema4.3.4. Intr-un triunghi dat ABC ,sa se inscrie un triunghi DEF, ale carui laturi sa fie paralele cu trei drepte date d₁, d₂ , d₃.

Demonstratie: ( fig. 4.3.4.) Se construieste mai intai un triunghi D’E’F’ avand laturile paralele cu cele trei drepte date si avand doua varfuri pe doua laturi ale triunghiului ABC.

Aceasta se realizeaza ducand printr-un punct arbitrar F’I (AB) o paralela la d₁,apoi prin punctul de intersectie al acesteia cu (AC) se duce o paralela la d₃ si, in sfarsit, prin F’ se duce o paralela la d₂, intersectia acestor drepte fiind D’. Se unesc punctele A si D’ si fie =BC AD’

Fig. 4.3.4.

In omoteteia de centru A si raport , triunghiul D’E’F’ se transforma in triunghiul DEF, care este triunghiul ce trebuie construit.

4.ALTE METODE

Problema 4.4.1. Sa se construiasca un trapez, cunoscand diagonalele lui, l si m, unghiul cuprins intre ele, α, si latura neparalela, a.

Demonstratie.

Presupunem problema rezolvata si trapezul ABCD este cel cautat.( fig. 4.4.1. )

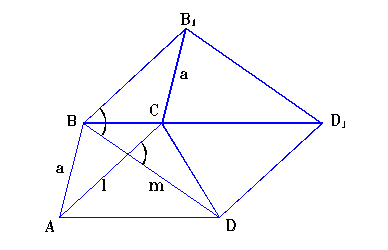Fig. 4.4.1.

Efectuam o translatie a triunghiului ABD in CB₁D₁, astfel incat varful A sa ocupe pozitia C. Ca rezultat, obtinem paralelogramul BB₁D₁D, cu laturile l si m, si unghiul cuprins intre ele , α, varful C al trapezului aflandu-se la distanta a de varful B₁ al paralelogramului.De aici, rezulta urmatoarea metoda de constructie a trapezului. Construim un segment BD=m si un unghi egal cu α, cu varful in punctul B. Pe cealalta latura a unghiului, luam un segment BB₁=l si ducem dreapta B₁D₁|| BD si dreapta DD₁|| BB₁, pana la intersectia lor in punctul D₁. Patrulaterul BB₁D₁D are laturile opuse paralele si, deci, este un paralelogram. Din varful B₁, ca centru, ducem un cerc de raza a si aflam punctul de intersectie C, al acestui cerc, cu diagonala BD₁ a paralelogramului.Unim punctul C cu punctele B si D, prin segmente de dreapta, si ducem dreptele DA || CD₁ si CA || DD₁, unde A este punctul de intersectie al acestor drepte. Unind A si B printr-un segment de dreapta, obtinem patrulaterul ABCD. Acesta este trapezul care satisface toate conditiile problemei, demonstratia fiind evidenta.

Posibilitatea rezolvarii problemei si numarul de solutii depind de existenta si numarul

punctelor de intersectie, C, ale dreptei BD₁ cu cercul de raza a si cu centrul in punctul B₁.

Problema 4.4.2 Sa se construiasca D ABC, cunoscand cele trei puncte A₁ , A₂ , A₃ , in care inaltimea, bisectoarea si mediana corespunzatoare varfului A intersecteaza cercul circumscris triunghiului.

Demonstratie( fig. 4.4.2. )

Fig. 4.4.2.

Presupunem problema rezolvata si fie ABC triunghiul cautat. Inaltimea, bisectoarea si mediana corespunzatoare varfului A intersecteaza cercul C(O,r), circumscris triunghiului in punctele date A₁, A₂ si A₃. Pentru ca A₂ este mijlocul arcului BC, rezulta OA₂|| AA₁. Notam

=OA₂ AA₃ . Este evident ca A’ este mijlocul segmentului BC.

Analizand figura alaturata, rezulta urmatoarea constructie. Se construieste cercul C(O, r), circumscris triunghiului A₁A₂A₃, apoi se uneste O cu A₂. Paralela prin A₁ la OA₂ intersecteaza cercul C(O,r) in punctul A. Se uneste A cu A₃ si fie =OA₂ AA₃. Perpendiculara in A’ pe OA₂ intersecteaza cercul C(O,r) in punctele B si C. Prin unirea lui A cu B si C se obtine triunghiul cerut de problema.

Problema 4.4.3 Construiti un triunghi, daca se cunosc:

a)      doua laturi si o mediana

b)      o latura si doua mediane.

Demonstratie: a) Cazul 1. Cunoastem doua laturi si mediana corespunzatoare

laturii a treia : a, b, m_c.Triunghiul ACD are laturile de lungimi a, b si 2m_c, deci poate fi construit si apoi punctul B se obtine evident ( fig. 4.4.3.a )

Fig. 4.4.3.a

Cazul 2. Cunoastem doua laturi si mediana uneia din laturi: b, c si m_b. Triunghiul ABN are laturile de lungimi c, si m_b, deci poate fi construit si apoi punctul C se obtine prelungind latura [AN] cu un segment de aceeasi lungime ( fig. 4.4.3.b )

Fig. 4.4.3. b

b) Cazul 1 . Cunoastem o latura si medianele corespunzatoare celor doua laturi : a, m_b, m_c Triunghiul BGC are laturile de lungimi a, si , deci poate fi construit. Punctul A se obtine prelungind , d d₂ = , d a =, d b = si [MN]s [RQ].

Presupunem d₁ || a si consideram NS || a, SI d_1, RT || d₁,TI b.Observam ca D MSN sDRTQ

Consideram punctele : = d₁ a, = d₁ b, = d₂ b.Rezulta ca AB || RT si

AR || BT T ARTB paralelogram, deci [AB] s [RT].

Analog SNCB paralelogram, deci [SN] s [BC]. Dar [SN] s [TQ], deci am obtinut [AB] s [RT] si [BC] s [ TQ].

Cum < ABC s < RTQ, obtinem:

DABC s D RTQ sD MSN, de unde: [AC] s [MN] s[ RQ].

Fig. 4.4.4.

Acum constructia devine evidenta. Analizam cazurile:

d₁ || a si distanta intre d₁ si d₂ nu este aceeasi cu distanta intre a si b-in acest caz problema nu are solutie.

d₁ || a si distanta intre d₁ si d₂ este aceeasi cu distanta intre a si b.Pentru orice dreapta care trece prin P si care nu este paralela cu d₁ conditia din enunt este indeplinita.

d₁ a . Fie = d₁ a, = d₁ b, = d₂ b, =d₂ a.Construim prin P paralele la diagonalele paralelogramului ABCD. Cele doua drepte sunt solutii ale problemei conform celor demonstrate mai sus.

Problema 4.4.5 Construiti un triunghi cunoscand a, h_a si B-C ( notatiile sunt cele uzuale).

Demonstratie : ( fig. 4.4.5.) Presupunem problema rezolvata ( B> C). Fie A₁ un punct astfel incat AA₁|| BC, m(< ACA₁) = B-C.

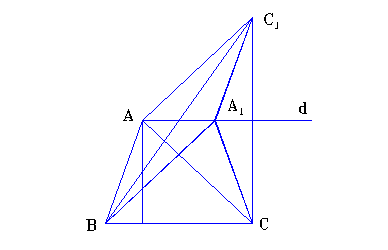Fig. 4.4.5.

Atunci : <ABC s < A₁CB, adica AA₁CB este trapez isoscel. Fie C₁ simetricul lui C fata de dreapta AA₁.Avem : [AB] s [ A₁C] s [ A₁C₁] si [AC₁] s [ AC ] s [ BA₁ ], deci patrulaterul ABA₁C₁ este paralelogram. Observam ca m(< BAC₁) =180⁰- m(< ABA₁)= 180⁰- (B-C), deci unghiul BAC₁ este cunoscut.

Acum putem sa expunem constructia : Consideram BC=a si dreapta d la distanta h_a de dreapta BC, d || BC. Fie CC’ BC, C₁C = 2h_a, iar C₁ este de aceeasi parte a lui BC ca si dreapta d. Consideram un arc capabil de unghiul 180⁰- (B-C) cu capetele in B si C₁; punctul A este intersectia acestui arc cu dreapta d.