Matrice si determinanti

Matrice si determinanti

Fie si doua multimi finite si X un inel cu unitate.

Valorile A (i,j) = a_ij se numesc elementele matricei A  si în mod traditional multimea ImA, organizata într-un tabel dreptunghiular cu m linii si n coloane, notat cu A, va fi numita matrice dreptunghiulara.

Pe scurt, matricea A va fi n 616f55g otata cu , , .

O matrice cu o singura linie sau coloana se va numi matrice linie respectiv matrice coloana sau vector.

Schimbarea liniilor în coloane în matricea A se numeste transpunerea lui A, iar matricea care se obtine se noteaza cu ^tA si se numeste transpusa matricei A.

Daca m = n, matricea A va fi numita matrice patratica, iar n va fi numit ordinul matricei.

În cele ce urmeaza, elementele matricelor folosite vor fi considerate din corpul numerelor reale R sau complexe C, notat cu K. Multimea matricelor de tipul m n cu elemente din K va fi notata cu M_{m n} (K).

Definim pe multimea M_{m n} (K) operatiile de adunare a doua matrice si produsul unei matrice cu un scalar.

Daca si sunt doua matrice de tipul m n atunci matricea A +B =: (a_ij + b_ij) este numita suma matricelor A si B. Proprietatile operatiei de adunare a doua matrice rezulta din proprietatile pe care le are suma din corpul K. Matricea cu toate elementele nule va fi notata cu O si o vom numi matricea zero, iar matricea va fi numita opusa lui A.

Daca l K si M_{m n} (K)atunci matricea

lA=: (l a_ij)

defineste produsul matricei A cu scalarul l

Daca A M_{m n} (K) si B M_{m n} (K) , atunci matricea de tipul m p, data de 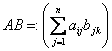, va fi numita produsul matricelor A si B .

Sa consideram multimea matricelor patratice de ordinul n, notata cu M_n (K). În multimea M_n (K ) produsul a doua matrice nu este comutativ. Daca matricele A, B M_n (K) satisfac proprietatea A B = B A , acestea vor fi numite comutabile.

O matrice patratica A cu proprietatea ^tA = A (^tA = -A) se numeste simetrica (antisimetrica). Orice matrice patratica poate fi scrisa în mod unic ca suma dintre o matrice simetrica si o matrice antisimetrica.

O matrice patratica cu toate elementele situate dedesubtul sau deasupra diagonalei principale nule se numeste matrice triunghiulara.

O matrice patratica pentru care: k astfel încât a_kk 0 si , , se numeste matrice diagonala.

Matricea diagonala în care a_ii = 1, se numeste matrice unitate de ordinul n si se noteaza cu I_n.

O matrice patratica cu proprietatea ^tAA = A^tA = I se numeste matrice ortogonala.

Daca A este o matrice patratica, atunci pot fi definite inductiv puterile lui A:

A° = 1, Aⁿ = A A^n-1, " n N*

Fie polinomul cu coeficientii din câmpul K. Numim polinom de matrice, matricea

unde A M _n(K) si I_n este matricea unitate de ordinul n.

De cum este definit determinantul unei matrice patratice A rezulta ca det(^tA) = detA, motiv pentru care orice proprietate referitoare la liniile unui determinant este adevarata si pentru coloane. Sa enuntam principalele proprietati ale determinantilor:

- daca elementele unei linii sunt reprezentate ca sume de câte doi termeni, atunci determinantul se descompune într-o suma de doi determinanti.

- daca elementele unei linii se multiplica cu un numar t, atunci determinantul se multiplica cu t. În general .

- daca într-un determinant se schimba doua linii între ele, atunci se schimba si semnul determinantului.

- valoarea unui detrminant nu se schimba daca la elementele unei linii adaugam o combinatie liniara formata cu elementele celorlalte linii.

Daca a_ij este un element al matricei A, notam cu D_ij determinantul obtinut prin suprimarea liniei i si a coloanei j, numit minorul elementului a_ij, iar cu complementul algebric al acestui element.

Calculul determinantului matricei A, folosind teorema de dezvoltare dupa linia i, , este dat de formula

Matricele patratice A M_n(K) pentru care detA 0 se numesc matrice nesingulare.

Matricea A^-1 cu proprietatile se numeste inversa matricei A. Matricea A este inversabila daca si numai daca A este nesingulara. Inversa matricei A se poate determina astfel: se calculeaza detA , se afla reciproca A* prin înlocuirea elementelor matricei ^tA cu complementii algebrici corespunzatori dupa care obtinem

Întrucât, în general, produsul a doua matrice nu este comutativ, avem (AB)^-1 = B^-1A^-1.

Multimea matricelor de ordinul n nesingulare împreuna cu operatia de înmultire a doua matrice formeaza un grup numit grupul liniar general de ordinul n, notat cu GL (n; K).

Grupul liniar general GL (n; K) contine câteva subgrupuri remarcabile:

GO(n; K) =

numit grupul ortogonal de ordinul n

SO(n; K) =

numit grupul ortogonal special de ordinul n.