ALTE DOCUMENTE
|
||||||||||
Minimizarea functiilor booleene
Introducere
Deoarece FB modeleaza functionarea circuitelor logice sau schemelor cu contacte
minimizarea poate determina reducerea costurilor de materializare a acestor scheme
Problema minimizarii
Fiind data o FB F (sau mai multe FB,F1,..,Fs), se cere sa se obtina o expresie a
FB (sau a FB F1,..,Fs) care sa īndeplineasca o conditie de minimalitate.
Criterii de minimalitate
aparitia unui numar minim de literale
aparitia unui numar minim de literale īntr-o expresie normal disjunctiva (suma de produse)
numar minim de termeni produs īntr-o expresie normal disjunctiva
diferenta minima īntre numarul de va 141c29b riabile īn forma normala si numarul de variabile īn forma negata (luata īn modul)
functia sa poata fi materializata cu numar minim de module dintr-un anumit set (porti logice, contactoare de un anumit tip,...)
timpii de īntārziere introdusi de circuitul materializat sa fie minim
etc
Problema minimizarii FB īn forma normal disjunctiva
Fiind data o FB īn forma normal disjunctiva sa se gaseasca o expresie tot īn forma
normal dijunctiva care sa aiba un numar minim de literale
Metoda 1
Se aplica proprietatile algebrei booleene
- distributivitatea
- idempotenta
- absorbtia
Metoda 1. Exemplu
Se da functia
f(x,y,z)=m0+m2+m3+m4+m5+m7=x'.y'.z'+ x'.y.z'+x'.y.z+ x.y'.z'+ x.y'.z+ x.y.z.
Adaugam m0+m7
f(x,y,z)=m0+m2+m3+m4+m5+m7=x'.y'.z'+x'.y.z'+x'.y.z+x.y'.z'+x.y'.z+ x.y.z+x'.y'.z' + x.y.z.
Combinam m0 si m2, m0 si m4, m3 si m7, m5 si m7 si obtinem:
f(x,y,z)=x'.z'(y+y')+y'.z'.(x+x') +y.z.(x'+x)+x.z.(y'+y)=x'.z'+y'.z'+y.z+x.z
Daca combinam m0 si m2, m4 si m5, m3 si m7 obtinem:
f(x,y,z)=x'.z'(y+y')+x.y'.(z'+z)+y.z.(x'+x)= x'.z'+x.y'+y.z
Daca īn mod similar grupam m2 cu m3, m4 cu m0 si m5 cu m7, se obtine pentru functia f expresia:
f(x,y,z)=x'.y+y'.z'+x.z
Observatii:
- pentru aceeasi functie am obtinut mai multe expresii redusefata de expresia initiala
- dintre cele trei expresii īnsa numai ultimele doua sunt expresii minime
- pentru o FB se pot obtine una sau mai multe expresii minime
Metoda 2. Diagrama Veitch-Karnaugh
este o metoda grafica pentru minimizarea cu usurinta a FB cu pāna la 6 variabile
casutele sunt aranjate īn astfel īncāt mintermii (maxtermii) sunt reprezentati īntr-o
dispozitie geometrica care permite evidentierea mintermilor adiacenti
fiecare casuta care are un 1 corespunde unui minterm a FCND a functiei
doua celule adiacente īn diagrama corespund la doi mintermi care difera īntre ei
doar prin forma unei singure variabile
perechea de valori de 1 se īncercuieste indicānd astfel ca mintermii corespunzatori
se combina rezultānd un singur termen
Regula prin care se determina cum pot fi grupate casutele continānd valori de 1 este urmatoarea:
- - o multime de 2i celule pot fi grupate daca exista i variabile ale functiei booleene care iau toate cele 2i combinatii posibile īn acea multime de casute īn timp ce celelalte n-i
variabile au aceeasi valoare pentru aceeasi multime de casute.
- Termenul corespunzator gruparii va contine cele n-i variabile īn care variabila este īn forma normala daca ea apare ca 1 pentru toate casutele gruparii si īn forma negata daca ea apare ca 0 pentru toate casutele gruparii.
Din punct de vedere grafic, regula de mai sus ne spune ca putem īncercui multimi dreptunghiulare avānd 2i valori de 1, prin aceasta īntelegānd si multimile dreptunghiulare obtinute daca muchiile opuse diagramei ar fi unite
Se pot determina variabilele si forma pe care acestea o au īn termenul rezultant:
- daca o īncercuire acopera casute īn care variabila este 0 atunci variabila apare īn termenul rezultant īn forma negata
- daca o īncercuire acopera casute īn care variabila este 1, atunci variabila apare īn termenul rezultant īn forma normala.
- daca o īncercuire acopera atāt casute īn care variabila este 0 cāt si casute īn care variabila este 1, atunci acea variabila nu mai apare īn termenul rezultant.
Metoda 2. Exemplul 1
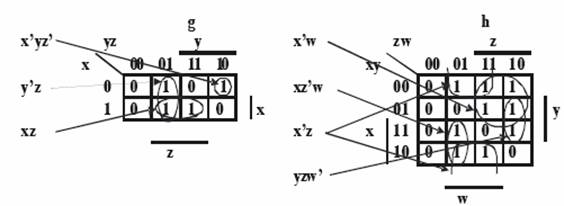
Confrom figurilor putem scrie:
g(x,y,z)=xz+y'z+x'yz'
h(x,y,z,w)=x'w+xz'w+x'z+yzw'
Teorema implicantilor primi
pentru o functie booleana, o expresie sub forma normala (suma de produse) minimala
este o suma de implicanti primi ai functiei.
Observatie:
- pentru a obtine o expresie minimala a functiei nu va trebui sa luam īn considerare termenii care nu sunt implicanti primi
Diagrame V-K si implicanti primi
Īn cadrul diagramei V-K, un implicant prim este reprezentat printr-o īncercuire
rectangulara de valori de 1 (conform regulii prezentate anterior) care daca īncercam sa o
marim (acoperind de doua ori mai multe casute) va cuprinde si valori de 0
Obtinerea expresiei minimale
expresie minimala se va obtine astfel prin alegerea īncercuirilor cele mai mari si astfel
īncāt fiecare valoare de 1 sa fie cuprinsa īn cāt mai putine īncercuiri
Metoda 2. Exemplul 2
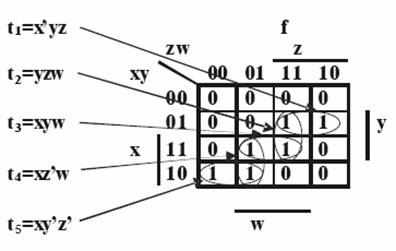
Metoda 2. Exemplul 2
Functia f se poate scrie ca suma tuturor implicantilor primi:
f(x,y,z)=t1+t2+t3+t4+t5
forma minimala se obtine īnsa ca suma:
f(x,y,z)=t1+t3+t5= x'yz+ xyw+ xy'z'
Metoda Quine McCluskey
Permite minimizarea unor functii cu numar mare de variabile
permite implementarea usoara a algoritmului cu ajutorul unui program pe calculator
Pondere a unui numar binar
Ponderea unui numar binar este numarul zecimal egal cu numarul de biti avānd
valoarea 1 din reprezentarea binara a respectivului numar
Exemplu
- Ponderea numarului binar x=1001 este 2
- Ponderea numarului binar x=1101 este 3
Algoritmul Quine-McCluskey
Se porneste de la forma canonica disjunctiva a functiei si se parcurg etapele:
1. se face conversia din zecimal īn binar a indicilor mintermenilor functiei binare
2. se īmpart numerele binare care reprezinta indicii mintermenilor īn grupuri, dupa ponderea fiecarui indice, īn sens crescator al ponderilor; grupurile se separa īntre ele prin linii orizontale si rezulta primul tabel
3. se compara fiecare numar binar din grupul de pondere i cu fiecare numar binar din grupul de pondere i + 1, pentru toate grupurile. Doua numere binare formeaza o noua grupare daca difera printr-un singur bit de acelasi rang. Gruparea noua se trece īntr-un al doilea tabel
4. De fiecare data cānd ponderea i de la punctul 3 creste cu o unitate, se trage o linie orizontala īn tabelul 2.Dupa completarea tabelului 2, se repeta comparatiile de la punctul 3, pentru elementele din tabel si rezulta tabelul 3, si asa mai departe
cānd se ajunge la un tabel care contine un singur numar binar, atunci termenul corespunzator este un implicant prim al functiei. Ceilalti implicanati primi se gasesc cautānd īn toate tabelele construite termenii care nu au fost folositi īn comparatii.
Algoritmul Q-M. Exemplu
Se considera functia
![]()
Algoritmul Q-M. Exemplu. Tabelul 1

Algoritmul Q-M. Exemplu. Tabelul 2

|