Model de dezvoltare in profil local

Model de dezvoltare în profil local

Pentru constructia unui model de dezvoltare locala se utilizeaza mai multi indicatori demografici si economici si anume:

-   &nb 414g64e sp;    ponderea populatiei active în totalul populatiei P_(a)

P_(a) = ;

în care: L - reprezinta forta de munca activa;

P_(t) - populatia totala din localitate;

Indicatorul are valoarea cuprinsa între 0 si 1:

0 < P_a < 1

Ponderea populatiei active în totalul populatiei trebuie sa aiba un nivel ridicat pentru a se asigura o continua crestere economica a microsistemului teritorial.

Modelul continua cu gradul de înzestrare tehnica a fortei de munca (K), care poate fi calculat cu ajutorul relatiei:

K =

în care: F_f - volumul fondurilor fixe;

L - resursele de munca.

Din ultimele doua relatii rezulta:

F_f = P_a . K . P_t

Daca P_a si K sunt marimi constante, atunci valoarea fondurilor fixe depinde de totalul populatiei din zona.

Se ia în calcul si nivelul productivitatii muncii în microsistemele teritoriale (W):

W = ,

în care: Q - volumul productiei obtinute;

L - forta de munca.

Productia obtinuta pe locuitor (q_l) reprezinta un alt indicator care arata nivelul de dezvoltare teritoriala, adica:

q_l = ;

din aceasta relatie rezulta q_l = P_a . W

Indicatorii dezvoltarii teritoriale prezentati sunt în realitate variabili. Deci se poate introduce în model indicatorul de crestere a resurselor umane (G):

G(P_t) = ( ) - rata cresterii populatiei;

G(L) = ( ) - rata cresterii populatiei active.

Daca ponderea fortei de munca în totalul populatiei (P_a) se considera constanta, rezulta:

G_(L) = G(P_t⁾

In model se pot introduce rate de crestere care reflecta schimbarile în dotarea si înzestrarea tehnica a fortei de munca, astfel:

G(F_f) = - rata cresterii fondurilor fixe;

G_(K) - rata cresterii gradului de înzestrare tehnica a resurselor de munca din teritoriu.

Data fiind relatia K = rezulta:

G_K = G(F_f) - G(L)

Daca se admite ipoteza constantei marimii P_(a) se poate obtine relatia:

G_(K) = G(F_f) - G(P_t)

In baza elementelor constituie se poate scrie modelul de dezvoltare locala în profil rural.

Functia particulara a productiei de tip Cobb-Douglas a microsistemului teritorial poate fi scris astfel:

Q = A L^1-α F_f^α

în care A si α sunt constante. Parametrul α este subunitar 0 < α < 1.

Din ultima relatie se poate scoate functia de productivitate a microsistemului local.

= A

Aceasta relatie se poate scrie si astfel:

W = P_a . A . K^α

Cu aceasta relatie se poate efectua simularea dezvoltarii microeconomice în diferite momente ale evolutiei. De exemplu, daca se iau în analiza doua momente ale evolutiei relatia de mai suss se poate scrie astfel:

W₁ = P_a . A . K₁^α

W₂ = P_a . A . K₂^α

Pentru intensitatea acumularii fondurilor fixe, relatiile de mai sus se pot scrie astfel:

K₁ = 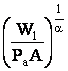; K₂ =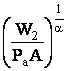

Astfel se poate anticipa, cu o aproximatie acceptabila evolutia înzestrarii tehnice a populatiei active teritoriale iar modelul în ansamblul sau poate sta la baza dezvoltarii spatiului rural în cadrul unei regiuni de dezvoltare.