ACADEMIA DE STUDII ECONOMICE
FACULTATEA DE ECONOMIE AGROALIMENTARA SI A MEDIULUI

REGRESIA MULTIPLA
De multe ori, studiul unui fenomen economic necesita introducerea mai multor variabile explicative. O variabila endogena se exprima, deci, in functie de mai multe variabile exogene. Metodele de regresie utilizate sunt in acest caz generalizari ale celor din capitolul anterior.
Modelul liniar al regresiei multiple
Consideram acum modelul:
(1)
![]() , t=1, 2, ,T
, t=1, 2, ,T
in care: Y reprezinta o variabila endogena;
X1, X2 ,, Xp sunt variabile exogene;
a1, a2 ,, ap sunt parametri necunoscuti care trebuie estimati.
Modelul
nu contine o constanta deoarece variabila Xp
poate fi considerata astfel ca xpt=1,
![]() (se numeste variabila
auxiliara).
(se numeste variabila
auxiliara).
Folosind notatiile:
 ,
, 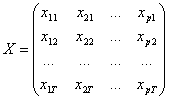 ,
,  ,
, 
ecuatia (1) se scrie sub forma matriceala:
(2) ![]() .
.
Ipoteze fundamentale
Ipotezele I1, I2 din capitolul II raman valabile: ceea ce era adevarat pentru xt este acum valabil pentru xit, i=1,2,,p.
Ipoteza I3 referitoare la variabilele exogene se modifica astfel:
a. absenta coliniaritatii variabilelor exogene:
Nu exista nici o multime de p numere reale ![]() , i=1,2,,p astfel incat
, i=1,2,,p astfel incat 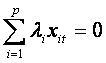 , t=1, 2, ,T.
, t=1, 2, ,T.
Matricea X de format (Txp) are in acest caz rangul p (T>p) si matricea (X'X), unde X' este transpusa lui X, este nesingulara, deci exista inversa ei (X'X)-1.
b.
Atunci cand ![]() , matricea
, matricea ![]() tinde catre o matrice
finita, nesingulara.
tinde catre o matrice
finita, nesingulara.
Determinarea estimatorilor parametrilor
Pentru
a scrie ecuatiile normale utilizam interpretarea geometrica data in capitolul
II. Ne propunem sa minimizam expresia 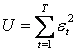 .
.
Fie vectorii Y, X1, X2,,Xp in spatiul ortonormat ![]() .
.
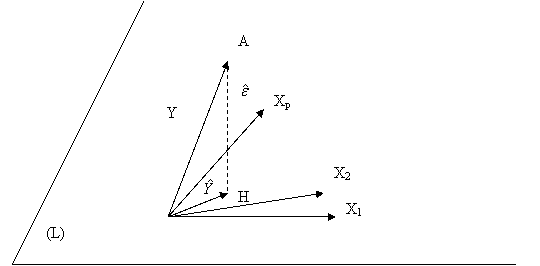
Vectorul
 apartine subspatiului (L) generat de vectorii X1, X2,,Xp.
Cantitatea
apartine subspatiului (L) generat de vectorii X1, X2,,Xp.
Cantitatea ![]() va fi minima atunci
cand vectorul
va fi minima atunci
cand vectorul ![]() este ortogonal la
subspatiul (L). Aceasta conditie se
traduce prin egalitatea cu zero a produselor scalare dintre vectorul
este ortogonal la
subspatiul (L). Aceasta conditie se
traduce prin egalitatea cu zero a produselor scalare dintre vectorul ![]() si orice vector din
subspatíul (L),deci si X1,X2,,Xp:
si orice vector din
subspatíul (L),deci si X1,X2,,Xp:
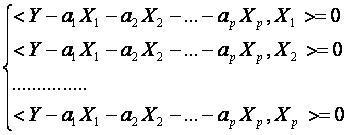
Efectuind produsele scalare, rezulta sistemul de ecuatii:

Sau, cu notatiile matriciale introduse:
X'Y=(X'X)a , de unde rezulta:
(3) ![]()
Proprietatile estimatorului ![]()
Aratam ca ![]() este un estimator
nedeplasat al lui a si deducem expresia
matricei de varianta si covarianta
este un estimator
nedeplasat al lui a si deducem expresia
matricei de varianta si covarianta ![]() .
.
a. transformam expresia (3) inlocuind Y prin expresia lui in functie de X:

Aplicand operatorul de medie expresiei (4), rezulta:
![]() .
.
Dar, ![]() conform I2,
deci
conform I2,
deci ![]() , adica
, adica ![]() este estimator
nedeplasat pentru a.
este estimator
nedeplasat pentru a.
b. Prin definitie:
![]() .
.
Din (4) rezulta: ![]() si
si ![]() pentru ca
pentru ca ![]() este o matrice
simetrica. Atunci:
este o matrice
simetrica. Atunci:
![]() si
si ![]() .
.
Insa ![]() este matricea de
varianta si covarianta a lui
este matricea de
varianta si covarianta a lui ![]() . Stim ca
. Stim ca ![]() (I este matricea unitate de ordinul T). Atunci rezulta:
(I este matricea unitate de ordinul T). Atunci rezulta:
![]()
Se
poate arata ca daca ipoteza a) din I3 ramane valabila cand ![]() , atunci
, atunci ![]() este estimator
convergent catre a.
este estimator
convergent catre a.
Propozitie. Estimatorul ![]() este cel mai bun
estimator liniar nedeplasat al lui a.
este cel mai bun
estimator liniar nedeplasat al lui a.
Pentru a arata aceasta proprietate vom construi un estimator liniar pentru a care sa aiba varianta minima si el va fi identic cu cel obtinut prin MCMMP. Fie a* un estimator liniar al lui a, adica a*=MY, unde M este o matrice cu coeficienti constanti de format (pxT). Estimatorul a* este nedeplasat daca:
![]()
adica ![]() pentru ca
pentru ca ![]() .
.
Pentru ca a* sa fie nedeplasat, trebuie ca (MX)=I (matricea unitate de ordinul p).
Construim acum matricea de varianta si covarianta a lui a*:
![]()
Dar,
![]() , deci
, deci ![]() ,
, 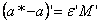 si
si ![]() . Pentru ca a* sa
fie de varianta minima, trebuie ca "urma" matricei (MM') sa fie minima, sub restrictia (MX)=I. Urma unei matrici este, prin definitie, suma elementelor de
pe diagonala principala. Notam Ur(X)
urma matricei X. Ur este un operator liniar (demonstrati!). Rezolvand
problema de extremum conditionat:
. Pentru ca a* sa
fie de varianta minima, trebuie ca "urma" matricei (MM') sa fie minima, sub restrictia (MX)=I. Urma unei matrici este, prin definitie, suma elementelor de
pe diagonala principala. Notam Ur(X)
urma matricei X. Ur este un operator liniar (demonstrati!). Rezolvand
problema de extremum conditionat:
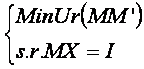
se obtine solutia ![]() , adica
, adica ![]() . Am gasit ca
. Am gasit ca ![]() .
.
Un astfel de estimator se numeste "estimator BLUE" (best liniar unbiaised estimator).
Determinarea unui estimator
nedeplasat al variantei ![]()
Varianta
reziduurilor ![]() fiind necunoscuta,
avem nevoie de un estimator al ei. Daca p
este numarul de coeficienti de estimat in model, se va arata ca:
fiind necunoscuta,
avem nevoie de un estimator al ei. Daca p
este numarul de coeficienti de estimat in model, se va arata ca:

Avem
ca: ![]() ;
;
![]() ;
;
![]() ;
;
![]() .
.
Dar:
![]() si
si ![]()
![]() .
.
Notam:
![]() .
.
G este o matrice de format (TxT) cu proprietatile G G (simetrica) si G G (idempotenta de grad 2). Am obtinut ![]() . Evaluam acum
. Evaluam acum ![]() , care sub forma matriceala este:
, care sub forma matriceala este: ![]() , unde gij este elementul matricii G situat la intersectia liniei i
cu coloana j.
, unde gij este elementul matricii G situat la intersectia liniei i
cu coloana j.
Atunci, rezulta ca:
![]() .
.
Insa,
![]() conform I2
si
conform I2
si ![]() .
.
Aratam
ca ![]() .
.
![]()
![]()
![]()
(permutarea
intre ![]() si
si ![]() este posibila datorita
formatului acestor matrici si proprietatilor operatorului Ur.)
este posibila datorita
formatului acestor matrici si proprietatilor operatorului Ur.)
In final rezulta:
![]() ,
, 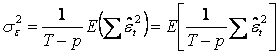 , astfel ca
, astfel ca  este estimator
nedeplasat al lui
este estimator
nedeplasat al lui ![]() .
.
T este numarul de observatii, p este numarul de parametri de estimat si relatia gasita o generalizeaza pe cea din capitolul II.
Teste si regiuni de incredere
Ipoteza
de normalitate a erorilor et fiind indeplinita, se pot generaliza
rezultatele obtinute la regresia simpla. Deoarece ![]() , rezulta ca
, rezulta ca ![]() este distribuita dupa
o lege normala in p dimensiuni, cu
media
este distribuita dupa
o lege normala in p dimensiuni, cu
media ![]() si dispersia
si dispersia ![]() . Pentru un estimator
. Pentru un estimator ![]() dat, avem ca:
dat, avem ca:
(*)
![]() urmeaza o lege normala
redusa N(0,1);
urmeaza o lege normala
redusa N(0,1);
(**)
![]() este distribuita c (hi-patrat) cu (T-p) grade de libertate.
este distribuita c (hi-patrat) cu (T-p) grade de libertate.
(***)![]() urmeaza o lege Student cu (T-p) grade de libertate.
urmeaza o lege Student cu (T-p) grade de libertate.
Legea
Student este utilizata in mod curent pentru a aprecia validitatea estimatorului
unui coeficient ai. De
exemplu, daca se testeaza ipoteza (H0:ai=0)
contra ipotezei (H1:ai![]() 0), pentru a accepta H1
trebuie ca
0), pentru a accepta H1
trebuie ca  , unde
, unde ![]() este valoarea tabelata
a variabilei t repartizata Student,
cu T-p grade de libertate, iar a este pragul de semnificatie.
este valoarea tabelata
a variabilei t repartizata Student,
cu T-p grade de libertate, iar a este pragul de semnificatie.
Observatie
Pentru T>30 si a=0,05, ![]() . Deci, daca
. Deci, daca 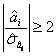 se accepta H1, adica ipoteza ca variabila
Xi are un coeficient ai semnificativ diferit de
zero.
se accepta H1, adica ipoteza ca variabila
Xi are un coeficient ai semnificativ diferit de
zero.
Mai general,
cand se pune problema de a sti daca un coeficient ai este diferit de o valoare particulara ![]() , se calculeaza raportul
, se calculeaza raportul  si se compara cu
si se compara cu ![]() .
.
Daca tcalculat>ttabelat concludem ca ![]()
Consideram
acum toti estimatorii ![]() :
:
variabila aleatoare ![]() este distribuita c cu p
grade de libertate;
este distribuita c cu p
grade de libertate;
(**)
variabila aleatoare ![]() urmeaza o lege
Fisher-Snedecor cu p si (T-p) grade de libertate.
urmeaza o lege
Fisher-Snedecor cu p si (T-p) grade de libertate.
La
fel ca la regresia liniara simpla, rezultatele anterioare permit construirea de
intervale de incredere relative la coeficientii ai, ca si a unui elipsoid de incredere relativ la
ansamblul coeficientilor in spatiul ![]() . Pentru ai,
intervalul de incredere, la pragul de seminificatie a este:
. Pentru ai,
intervalul de incredere, la pragul de seminificatie a este:


![]()
![]()
iar pentru ansamblul coeficientilor, ecuatia elipsoidului de incredere este: F=F(a,p,T-p).
Aceleasi
principii conduc la determinarea de regiuni de incredere relative la un numar
oarecare de coeficienti din model. Daca q
este numarul coeficientilor retinuti, in spatiul ![]() , avem ecuatia F1=F(a,q,T-p), unde:
, avem ecuatia F1=F(a,q,T-p), unde:
![]() .
.
cu
![]() extras din vectorul
extras din vectorul ![]() si
si ![]() extrasa din
extrasa din ![]() :
:
Daca
dorim sa testam, la pragul de semnificatie a, ipoteza (H0:aq=![]() ) contra ipotezei (H1:aq
) contra ipotezei (H1:aq![]() ), atunci daca:
), atunci daca:
![]()
se accepta ipoteza H0 (![]() se extrage din tabelele distributiei Fisher-Snedecor).
se extrage din tabelele distributiei Fisher-Snedecor).
Observatie
Se observa
ca valoarea tabelata F depinde de ![]() si nu de
si nu de ![]() . Rezulta ca expresia
. Rezulta ca expresia 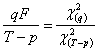 face sa apara la
numitor
face sa apara la
numitor ![]() distribuita c cu (T-p)
grade de libertate.
distribuita c cu (T-p)
grade de libertate.
Previziunea variabilei endogene
Daca presupunem cunoscute la un moment q valorile (x1q, x2q,, xpq) atunci previziunea variabilei endogene va fi:
![]() .
.
Eroarea de previziune va fi variabila aleatoare:
![]() .
.
Se constata ca media erorii de previziune este zero:
![]() ,
,
iar varianta erorii de previziune este:
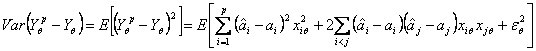
deoarece ![]() si
si ![]() sunt necorelate (
sunt necorelate (![]() nu depind decat de
nu depind decat de ![]() ), t=1,2,,T si T<q
), t=1,2,,T si T<q
Deducem ca:
 ,
,
iar sub forma matriciala:
![]() , adica:
, adica:
![]() ,
,
unde: ![]()
Observatie:
Se arata ca daca T
este finit si et sunt normal distribuite, atunci ![]() este distribuita
normal in p dimensiuni. Daca
ipotezele nu sunt indeplinite, atunci cind
este distribuita
normal in p dimensiuni. Daca
ipotezele nu sunt indeplinite, atunci cind ![]() , vectorul
, vectorul ![]() urmeaza o distributie
normala cu media egala cu zero.
urmeaza o distributie
normala cu media egala cu zero.
Coeficientul de corelatie multipla R. Analiza variantei
Si in acest caz, ecuatia variantei se scrie:
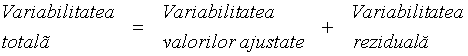
![]()
Coeficientul de corelatie multipla R are definitia:
 .
.
Din
reprezentarea geometrica facuta, rezulta ca ![]() ,
,
dar stim ca  si
si ![]() , rezultand ca:
, rezultand ca: ![]() , ceea ce arata ca vectorul rezidual
, ceea ce arata ca vectorul rezidual ![]() este acelasi si pentru
valorile (Y,X) si pentru valorile
centrate fata de medie
este acelasi si pentru
valorile (Y,X) si pentru valorile
centrate fata de medie ![]() . Cu alte cuvinte, daca efectuam regresia pe ecuatia
generala, cu variabilele necentrate sau o efectuam cu variabilele centrate pe
media lor, estimatorul
. Cu alte cuvinte, daca efectuam regresia pe ecuatia
generala, cu variabilele necentrate sau o efectuam cu variabilele centrate pe
media lor, estimatorul ![]() si vectorul rezidual
si vectorul rezidual ![]() sunt aceeasi.
sunt aceeasi.
Observatie:
Cand se
centreaza valorile X si Y, vectorul ![]() nu contine ultimul
estimator
nu contine ultimul
estimator ![]() . Constanta
. Constanta ![]() dispare cand se
centreaza variabilele. Considerarea modelului fara constante, cu variabilele
necentrate pe media lor, poate conduce la valori ale lui
dispare cand se
centreaza variabilele. Considerarea modelului fara constante, cu variabilele
necentrate pe media lor, poate conduce la valori ale lui ![]() care ies din
intervalul (0,1).
care ies din
intervalul (0,1).
Expresia matriciala a coeficientului de corelatie multipla este:
![]() , dar
, dar ![]() .
.
![]() si coeficientul
devine:
si coeficientul
devine:
![]() .
.
Coeficientul
![]() arata rolul jucat de
toate variabilele exogene asupra evolutiei variabilei endogene. El este cu atat
mai bun cu cat e mai apropiat de 1.
arata rolul jucat de
toate variabilele exogene asupra evolutiei variabilei endogene. El este cu atat
mai bun cu cat e mai apropiat de 1.
Dar,
judecarea calitatii unui model doar prin valoarea lui ![]() poate duce la erori
grosiere. El mascheaza uneori influenta variabilelor exogene luate separat
asupra variabilei endogene si nu poate sa se substituie studiului estimatorilor
coeficientilor modelului. Patratul coeficientului de corelatie multipla nu tine
cont nici de numarul de observatii (T)
si nici de numarul variabilelor explicative (p). Ori, se poate foarte bine ca, avand aceleasi observatii asupra
variabilei endogene sa consideram doua modele distincte, in al doilea facand sa
apara un numar de variabile explicative noi. In aceasta a doua regresie
coeficientul de corelatie multipla nu poate decat sa creasca (pentru ca
variabilitatea explicata prin regresie creste).
poate duce la erori
grosiere. El mascheaza uneori influenta variabilelor exogene luate separat
asupra variabilei endogene si nu poate sa se substituie studiului estimatorilor
coeficientilor modelului. Patratul coeficientului de corelatie multipla nu tine
cont nici de numarul de observatii (T)
si nici de numarul variabilelor explicative (p). Ori, se poate foarte bine ca, avand aceleasi observatii asupra
variabilei endogene sa consideram doua modele distincte, in al doilea facand sa
apara un numar de variabile explicative noi. In aceasta a doua regresie
coeficientul de corelatie multipla nu poate decat sa creasca (pentru ca
variabilitatea explicata prin regresie creste).
O
definire mai precisa a lui ![]() , care tine cont de T si p este:
, care tine cont de T si p este:
![]() .
.
![]() se numeste coeficient de corelatie multipla corectat.
se numeste coeficient de corelatie multipla corectat.
daca p=1, atunci ![]() ;
;
daca p>1, atunci ![]() ;
;
![]() poate scadea prin
introducerea in model a unei noi variabile exogene;
poate scadea prin
introducerea in model a unei noi variabile exogene;
![]() poate lua si valori
negative, daca
poate lua si valori
negative, daca ![]() .
.
Analiza variantei
Atunci cand studiem rolul jucat de exogene asupra evolutiei endogenei, ne putem intreba care este partea de variabilitate explicata de una sau mai multe variabile exogene.
Reluam modelul initial:
(1)
![]() , t=1, 2, ,T
, t=1, 2, ,T
si consideram q variabile printre cele p, pe care le indexam de la 1 la q:
(2)
![]() .
.
Variabilitatea ne-explicata de cele q exogene in modelul (1) este variabilitatea reziduala asociata modelului (2).
Fie:
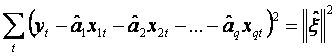
Variabilitatea ne-explicata de cele p exogene din modelul (1) este:
![]()
Variabilitatea explicata de cele (p-q) exogene din modelul (1) atunci cand a1,,aq sunt estimati cu modelul (2) este atunci:
![]()
Stim
ca ![]() , adica
, adica ![]() .
.
Rezultatele se grupeaza, adesea, intr-un tabel de analiza a variantei:
|
Sursa variabilitatii |
Suma patratelor corespunzatoare acestei surse |
Numarul gradelor de libertate |
Media patratelor asociate |
|
1. X: multimea celor p exogene |
|
p |
|
|
2. |
|
T-p |
|
|
3. Y: variabila endogena |
|
T |
|
|
4. (p-q) variabile exogene dintre cele p |
|
p-q |
|
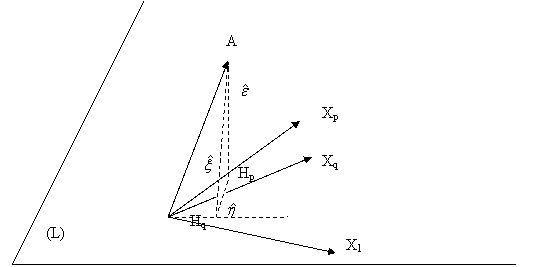
In figura anterioara avem:
![]() este proiectia lui Y pe subspatiul (L) ai carui vectori
generatori sunt X1,X2,,Xp.
este proiectia lui Y pe subspatiul (L) ai carui vectori
generatori sunt X1,X2,,Xp.
![]() este proiectia lui Y pe subspatiul generat de X1,X2,,Xq.
este proiectia lui Y pe subspatiul generat de X1,X2,,Xq.
Hq apartine lui (L) si triunghiul AHpHq este dreptunghic in Hp.
![]() si
si ![]() , iar
, iar ![]() este chiar
este chiar ![]() .
.
|