NUMERE COMPLEXE

NUMERE COMPLEXE

Forma algebrica

Se numeste numar complex (în forma algebrica), un numar de forma , unde ,

, se numeste partea reala a lui si se noteaza iar se numeste partea imaginara a

lui , se numeste coeficientul partii imaginare si se noteaza . Multimea numerelor complexe se noteaza 141e42b cu . Un numar complex se numeste pur imaginar daca este de forma , unde (este nenul si partea reala este egala cu 0). Notam multimea numerelor complexe pur imaginare cu .

Daca , unde este un numar complex, atunci se numeste conjugatul lui , numarul complex , se numeste modulul lui , numarul real pozitiv .

Observatie. Atât partea reala cât si cea imaginara a unui numar complex sunt numere reale. Doua numere complexe sunt egale daca si numai daca au atât partea reala cât si cea imaginara egale.

Fie si doua numere complexe, atunci:

, .

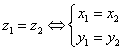
Daca , atunci .

Puterile lui :

.

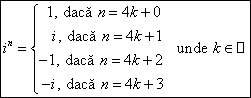Proprietati ale numerelor complexe:

,

, ; , ;

, , ;

, ,, , , ;

,;

, ; ; , ;

, ; , ;

, , .

, .

Rezolvarea ecuatiei de gradul II cu coeficienti reali

Fie , unde , , . În functie de valorile lui se disting 3 cazuri:

Daca , ecuatia are doua radacini reale distincte ;

Daca , ecuatia are doua radacini reale egale ;

Daca , ecuatia nu are radacini reale, în schimb are doua radacini complexe conjugate:

.

Rezolvarea ecuatiei de gradul II cu coeficienti complecsi

Fie , unde , un numar complex. Se numeste radacina patrata a lui un numar complex , unde cu proprietatea ca .

Observatie. Pentru determinarea lui pornim de la egalitatea

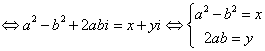. Pentru a usura determinarea lui putem trece la modul în

egalitatea initiala: si obtinem un

nou sistem: .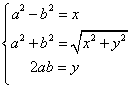

Observatie. Orice numar complex nenul admite doua radacini patrate opuse.

Fie , unde , , solutiile ecuatiei sunt solutiile ecuatiei sunt date de , unde este radacina patrata a lui ().

Forma trigonometrica

Reprezentarea numarului complex sub forma : ,

, se numeste forma trigonometrica a lui , se numeste argumentul redus a lui z si se noteaza cu , , .

Observatie. Daca înlocuim cu , unde , atunci relatia de mai sus ramâne valabila si deci exista o infinitate de valori astfel încât . Orice numar real care verifica relatia precedenta se numeste argument al lui . Multimea argumentelor lui se noteaza . Deci .

Fie un numar complex, atunci (conjugatul).

Fie si doua numere complexe, , atunci:

, ;

, ;

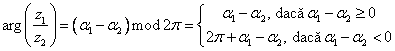(formula lui Moivre), daca , atunci , iar radacinile de ordinul sunt , unde .

Radacinile de ordinul ale unitatii

sunt solutiile ecuatiei cu

,

Imaginile geometrice ale radacinilor de ordinul ale unitatii sunt vârfurile unui poligon regulat cu n laturi înscris în cercul

Notam - multimea radacinilor de ordinul ale unitatii. Avem:

( are elemente)

, unde , .

.

Interpretarea geometrica a numerelor complexe

Numarul complex este bine determinat de doua numere reale si care pot fi gândite drept coordonate ale unui punct din planul în care am fixat un sistem de axe

ortogonale (ca în figura de mai jos).

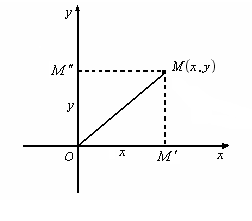Este usor de vazut ca aceasta corespondenta este bijectiva. Asadar avem aplicatia : .

se numeste imaginea geometrica a numarului complex . Numarul complex se numeste afixul punctului . Prin aceeasi aplicatie multimii numerelor reale îi corespunde axa , iar multimii numerelor complexe pur imaginare îi corespunde axa . Din aceste motive, axa se numeste axa reala, iar axa se numeste axa imaginara. Planul ale carui puncte se identifica cu numerele complexe prin corespondenta de mai sus se numeste planul complex. Modulul numarului complex este lungimea segmentului , fiind imaginea geometrica a lui .