O problema de optimizare a activitatilor de transport

O problema de optimizare a activitatilor de transport

Doua fabrici de conserve Fi unde i = (1,2), aprovizioneaza trei unitati co 747j99h merciale engros Cj unde j = (1, 2, 3) si plateste transportul pe unitatea de conserva, astfel: de la F la cele trei unitati comerciale cu 200, 250, 300 lei, iar de la F2 la cele trei centre cu 400, 200 si 100 lei.

Īn fabrica F se realizeaza 40% din īntreaga cantitate, iar īn F Conform necesitatilor, unitatile comerciale Cj absorb 20%, 30%, 50% din productia de conserve.

Se cere sa se gaseasca un plan de repartitie a produsului fabricat īn Fi unde i = (1,2), astfel īncāt costul total de transport sa fie minim.

Pentru rezolvare se formeaza īn prealabil planul de transport conform datelor din problema.

Grafic, planul de transport poate arata ca īn figura urmatoare:

C1

F1

F2

C3

C2

Īn continuare, se noteaza cu Xij cantitatea de produs transportata de la F , F la cele trei centre. Ţinānd seama de restrictiile problemei se poate scrie urmatorul sistem de ecuatii:

Legenda:

F - reprezinta fabrica

C - reprezinta centrul engros X + X + X X + X + X

X + X

X + X

X + X

Xij 0 (i = 1,2 ; j = 1 )

Se ia īn considerare ca īntreaga cantitate de conserve produsa īn cele doua fabrici F , F este transportata la cele trei centre (C , C , C

Functia de eficienta, care reprezinta costul total al transportului este:

f min) = 200X + 250X + 300X + 400X + 200X + 100X

Din sistemul de egalitati se pot exprima necunoscutele Xij, īn functie de X si X , astfel:

X = 20 - X

X = 30 - X

X = 40 - X - X

X = 60 - (30 - X12 ) - (20 - X ) = 10 + X + X

Cu aceste valori, functia de eficienta f(min) devine:

f(min) - 400 X - 150X

Daca se noteaza X = X si Y = X si tinānd seama de conditia de nenegativitate (Xij 0) vom obtine:

40 - X - Y 0 X + Y - 40 0

20 - X 0 X 20

30 - Y 0 sau Y 30

X + Y + 10 0 X + Y + 10 0

X 0 ; Y 0

S-a ajuns astfel la o problema cu doua necunoscute.

Pentru reprezentarea grafica se stabilesc dreptele:

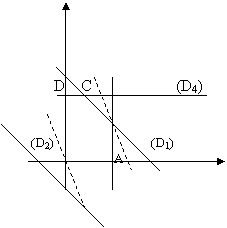y (D ): X + Y - 40 = 0

(D X + Y + 10 = 0

(D X = 20

(D Y = 30

B Functia de eficienta se poate scrie sub forma:

0 (D₃) x unde

Coordonatele punctului B fac minima functia obiectiv B(

Solutia problemei prevede urmatorul plan de transport:

Rezulta ca fabrica F trebuie sa trimita cantitatea īn mod egal la centrele C si C , iar F va trimite produsele numai la centrele C si C

Functia de eficienta va fi :

f(min) =