OPERATII CU VECTORI
1. Care sunt elementele unui vector ? Dati un exemplu de vector si indicati elementele lui.
2. Cum se reprezinta suma a doi vectori? Aratati doua metode. Deduceti expresia modului sumei a doi vectori.
3. Enumerati operatiile pe care le cunoasteti si la care participa si vectori. Verificati pentru fiecare din aceste operatii comutativitatea si asociativitatea.
4. Demonstrati ca proiectia sumei a doi vectori pe o axa este egala cu suma proiectiilor celor doi vectori pe aceeasi axa.
5. Exprimati modulul sumei a doi vectori cunoscand componentele lor pe doua axe:
a) rectangulare
b) care formeaza intre ele unghiul a
6. Care sunt lungimea si directia unei deplasari intre punctele de coordonate: A(1; 2) si B(3; 4)?
7. Calculati modulul si reprezentati vectorul rezultat in urma operatiei:
F = F1 + F2
unde F1= 2 N , F2 = 3 N, a = 180
8. Deduceti expresia produsului scalar a doi vectori in functie de componentele celor doi vectori pe trei axe rectangulare.
9. Deduceti expresia modulului produsului vectorial a doi vectori in functie de componentele vectorilor pe trei axe rectangulare.
10. Demonstrati urmatoarele egalitati:
a) a ( a x b ) = 0
b) a ( b x c ) = ( a x b ) c
c) a x ( b x c ) = b( a c ) - c( a b
c
11.Aratati ca volumul unui paralelipiped se calculeaza
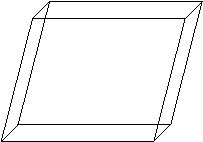cu relatia:
V = ( a x b ) c
12. Multimea vectorilor echipolenti intre ei o numim vector liber. Se numesc echipolenti doi vectori care au: a) aceeasi directie; b) acelasi sens; c) aceeasi marime. ' a echipolent cu b' se scrie: a b.
Aratati ca relatia de echipolenta are proprietatile:
a a (reflexivitate)
**a bT b a ( simetrie)
*** ( a b si b c ) T a c ( tranzitivitate).
13. Fie doi vectori echipolenti AB si CD, nesituati pe aceeasi dreapta. Sa se arate ca
AC BD.
14. Sa se afle locul geometric al punctului M' stiind ca MM' reprezinta un vector liber dat t, iar punctul M descrie un segment dat AB (acest loc se numeste transformatul prin translatia t a segmentului AB).
15. Aceeasi problema cand M parcurge multimea punctelor interioare dreptunghiului dat ABCD.
16. Sa se afle transformatul A'B'C'D' al paralelogramului ABCD prin translatia care duce pe A in C. Unde este transformatul lui O, centrul paralelogramului? Sa se deseneze vectorii AA', BB', CC', DD', OO'. Sa se arate ca ei constituie diferiti reprezentanti ai aceluiasi vector liber.
17. Fie vectorii a (a = 4) si b (b = 5) si a = 60 unghiul dintre directiile lor. Calculati modulul sumei lor, al diferentei, proiectia unuia pe celalalt, unghiul dintre suma si unul dintre vectori, unghiul dintre suma si diferemta, proiectia diferentei pe produsul lor vectorial.
18. Doi vectori au modulele egale cu modulul sumei lor. Calculati diferenta lor.
19. Fie vectorii a = 3 u + 5 v si b = 4 u - 6 v, unde u si v sunt versorii axelor care formeaza unghiul a = 60 una fata de alta. Calculati produsul lor scalar si pe cel vectorial. Duceti proiectiile celor doi vectori pe axe. Construiti suma celor doi vectori si determinasi-i valoarea.
20. Aratati in minimum cinci modalitati distincte ca vectorii a = 6 i + 2 j si b = 3 i - 9 j sunt perpendiculari.
21. Aratati ca intr-unparalelogram suma patratelor laturilor este egala cu suma patratelor diagonalelor.
22. Fie vectorii a = 4 i + 6 j , b = 5 j - 2 k si c = 2 i - 4 j + 5 k. Aflati:
a) Versorii vectorilor;
b) Produsele lor scalare si vectoriale;
c) Proiectiile reciproce. Produsele lor mixte
d) Unghiurile dintre ei, dintre ei sisumele lor si diferentele lor.
e) Fie vectorul d = p i + q j + r k. Determinati p, q, r a. i. d sa fie perpendicular pe planul determinat de vectorii b si c.
23. Daca exista trei numere m, n, p, nu toate nule, astfel incat v = ma + nb + pc , se spune ca vectorul v este o combinatie liniara a vectorilor a, b, si c.
a) Sa se scrie vectorul v = 5i - j ca o combinatie liniara a vectorilor a = i + j si
b -i +2j.
b) Sa se scrie vectorul v = i - 18j + k ca o combinatie liniara a vectorilor:
a = 2i + j - k, b = -i + 0,5j + 3k, c = 0,25i - 5j - k.
24. Vectorii a, b, c sunt liniar dependenti daca exista 3 numere m, n, p, nu toate nule, astfel incat : ma + nb + pc = 0. {n caz contrar sunt liniar independenti.
Sa se arate ca vectorii a = i + j + k, b = -i -2j + 3k, c = -0.25i - j +(11/4) k sunt liniar dependenti.
|
