ALTE DOCUMENTE
|
||||||||||
Optimizarea unei activitati de transport
În programarea si optimizarea proceselor de productie în agricultura, problemele de transport ocupa un loc important.
Pentru a întelege bine problemele multiple care le ridica eficientizarea activitatilor de transport, este necesar sa se cunoasca câteva probleme teoretice. Sa plecam de la urmatorul exemplu: sa consideram ca un anumit produs agricol este stocat la un numar de centre de depozitare "m" notate cu Ai în care i = (1,m) în cantitati ai
Produsul este cerut în "n" centre de consum Bj, unde j = (1,n) in cantitati bj Cunoscând costul de transport Cij al produsului de la depozitul Ai la depozitul Bj se cere sa se determine cantitatile Xij de produse ce urmeaza sa fie repartizate de la Ai la Bj, astfel ca disponibilul din stoc sa fie epuizat în fiecare depozit, cererea sa fie satisfacuta la centrele de consum, iar costul de transport al pro 757e48h dusului sa fie minim.
Sa presupunem ca ![]() , adica disponibilul din depozite este
egal cu cererea centrelor de consum (problema
de echilibru).
, adica disponibilul din depozite este
egal cu cererea centrelor de consum (problema
de echilibru).
Costul total al transportului se obtine din suma produselor dintre costurile Cij si necunoscutele Xij (cantitati ce pot si trebuie sa fie transportate).
Daca notam cu "f" costul total de transport, vom avea:
f = C X + C X + ..+ C1nX1n + C X + C X +..+ C2nX2n + Cm1Xm1 + Cm2Xm2 + ..+ CmnXmn
Sub forma restrânsa, functia se poate scrie astfel:
F = ![]() în care Xij
în care Xij ![]()
Depozitul Ai nu poate expedia celor n centre de consum decât cel mult cantitatea de care dispune, adica aij din produsul depozitat, deci:
Ai = Xi1+ Xi2 +....+ Xin sau ![]()
Centrului de consum Bj nu i se poate repartiza decât cantitatile de care are nevoie si pe care le poate primi de la cele "m" depozite adica bj, rezulta ca:
x1j+x2j+............+xmj=bj sau ![]()
Fata de cele prezentate se poate scrie formula de optimizare a problemei de transporturi în felul urmator:
![]() in
conditiile
in
conditiile
 unde
unde 
Orice solutie care satisface pe (C) se numeste solutie posibila a problemei de transport si solutia care minimizeaza functia de eficienta se numeste solutie optima.
Multitudinea solutiilor posibile ale oricarei probleme de transport ( C ) este o multime nevida si marginita. Sistemul de ecuatii dat de conditiile problemelor de transport ( C ) contine m + n - 1 ecuatii independente cu m,n necunoscute.
Datele unei probleme de transport pot fi prezentate sub forma de tabel, astfel:
|
B B ........................ Bj .......... ..... ...... ..Bn |
ai |
|
|
A |
C X C X .......C1jX1j........C1nX1n |
a |
|
A |
C X C X ..........C2jX2j........C2nX2n |
a |
|
Ai |
Ci1Xi1 Ci2Xi2............CijXij.........CinXin |
Ai |
|
Am |
Cm1Xm1 Cm2Xm2.......CmjXmj.........CmnXmn |
am |
|
b b .......bj........bn |
Problemele de transport se întâlnesc des în activitatile de distribuire a marfurilor si repartitiilor materiilor prime între diversi consumatori sau integratori.
Sa luam spre exemplificare un caz particular a metodei expuse:
În doua depozite Ai unde i = (1,2) se gasesc 300 tone, respectiv 500 tone îngrasaminte chimice care trebuie transportate la trei exploatatii agricole pentru a le utiliza în procesul de productie agricol Bj, unde j = (1,23), în cantitatile solicitate de acestea, respectiv 200,400 si 200 tone.
Costul transportului unei tone de îngrasamânt de la A la Bj este de 6,14,5 unitati monetare, iar de la A la Bj de 6,9,8 unitati monetare.
Se cere sa se întocmeasca un plan de transport optim, adica sa se asigure necesarul de îngrasaminte fiecarei unitati agricole, iar costul sa fie minim.
Modul de rezolvare poate fi urmatorul:
Se noteaza cu Xij (i= 1,2 si j = 1,2,3) cantitatile de îngrasaminte (tone) care trebuie transportate de la depozite (Ai) la unitatile de productie agricole (Bj
Se scriu restrictiile problemei:
X11 + X12 + X13 = 300
X21 + X22 + X23 = 500
X11 + X21 = 200
X12 + X22 = 400
X13 + X23 = 200
Xij![]()
Se noteaza cu "f" costul total al transporturilor si se tine seama de costul transportului unei tone de combustibil de la depozitul Ai la unitatea agricola Bj Se obtine:
f = 6X + 14 X + 5X + 6X + 9X + 8X
Pentru simplificare se fac notatiile X=X si Y = X relatiile stabilite se pot scrie astfel:
X = 200 - X
X = 400 - Y
X = 300 - X -Y
X = 200 - 300 + X +Y ![]() X = -
100 + X + Y
X = -
100 + X + Y
Deoarece solutia
sistemului format trebuie sa fie nenegativa (Xij ![]() 0) se
obtine:
0) se
obtine:
300 - X - Y ![]() 0 X + Y
0 X + Y ![]() 300
300
200 -X ![]() 0 sau X
0 sau X ![]() 200
200
400 - Y ![]() 0 Y
0 Y ![]() 400
400
- 100 + X +Y ![]() 0 X + Y
0 X + Y ![]() 100
100
X ![]() 0 :Y
0 :Y ![]() X
X
![]() 0 :Y
0 :Y ![]()
În continuare se exprima functia obiectiv "f" prin X si Y:
f = 6X + 14Y + 5(300 - X - Y) + 6(200 - X) + 9(400 - Y) + 8(-100 + X + Y)
Din efectuarea calculelor se obtine:
f = 3X + 8Y + 5.500
Valorile necunoscutelor X si Y satisfac sistemul de inegalitati si reduce la minimum costul transportului exprimat prin "f".
Mai întâi se reprezinta grafic dreptele:
(D1)![]() X + Y
- 300 = 0
X + Y
- 300 = 0
(D2)![]() X + Y
- 100 = 0
X + Y
- 100 = 0
(D3)![]() X =
200
X =
200
(D4)![]()
![]() Y = 400
Y = 400
y (D4)
(D3)
A
0 (D1) x
(D2)
sau
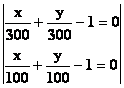

Functia obiectiv "f" se poate scrie sub forma:
![]() unde
unde ![]() si
reprezentam grafic dreapta
si
reprezentam grafic dreapta ![]()
Se duc drepte paralele cu dreapta (d ) si se determina cea care corespunde problemei propuse. Din grafic se observa ca este cea care trece prin punctul A. Punctul A are coordonatele x =200 , y=0 .
Planul optim de transport este urmatorul:
|
Unitati Depozite |
U |
U |
U |
|
Dep 1 A1 | |||
|
Dep 2 A2 |
Functia de minimizare a cheltuielilor de transport este:
![]()
Deci, costul minim va fi de 6100 unitati monetare.
|