PLANUL sI DREAPTA ÎN SPAŢIU

Ecuatia generala a unui plan

Tipuri de ecuatii ale unui plan

Ecuatiile canonice ale dreptei în spatiu

Tipuri de ecuatii ale unei drepte

Probleme metrice

2.1. Ecuatia generala a unui plan

Ecuatia generala a unui plan în spatiu este data de urmatoarea teorema:

Teorema 1. Un punct M(x, y, z) E se gaseste într-un plan p daca si numai daca verifica ecuatia , cu A, B, C , nenule simultan.

Demonstratie:

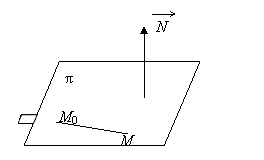
Fie un plan p din E₃ si fie un punct M₀(x₀, y₀, z₀) p fixat.

Fie, un vector nenul perpendicular pe plan,

Fie un punct oarecare M(x, y, z) E₃ din planul p.

Avem atunci:

Întrucât , este perpendicular pe orice dreapta din plan, deci

Ax + By + Cz + (-Ax₀ - By₀ - Cz₀) = 0, adica Ax + By + Cz + D = 0, unde
D = -Ax₀ - By₀ - Cz₀.

Reciproc, fie . Vom arata ca multimea S reprezinta un plan. Într-adevar, daca si , atunci avem:

Fie . Evident este nenul, iar din relatia de mai sus rezulta ca este perpendicular pe , oricare ar fi . Asadar, S reprezinta planul care trece prin si este perpendicular pe . Reamintim ca prin directia dreptei d întelegem orice dreapta care este paralela sau coincide cu dreapta d.

Ecuatia se numeste ecuatia generala a planului.

Vectorul se numeste normala la planul p

Cazuri particulare de plane

1) Ecuatia planelor de coordonate:

Planul xOy are ecuatia z = 0.

Planul xOz are ecuatia y = 0.

Planul yOz are ecuatia x = 0.

2) Ecuatia unui plan paralel cu planele de coordinate:

Un plan are ecuatia z = z₀ (constant).

Un plan are ecuatia x = x₀ (constant).

Un plan are ecuatia y = y₀ (constant).

3) Ecuatia unui plan ce trece prin originea O(0, 0, 0) :

Daca originea O apartine planului si înlocuind în ecuatia generala a planului rezulta ca D = 0, si deci ecuatia planului este: Az + By + Cz = 0.

4) Ecuatia unui plan paralel cu axele de coordonate

De exemplu: un plan paralel cu Ox, are ecuatia By +Cz + D = 0.

Într-adevar, daca este un vector normal la plan, atunci , deci

Asadar ecuatia planului paralel cu axa Ox este: By + Cz + D = 0.

În mod analog, ecuatia planului paralel cu axa Oy este: Ax + Cz + D = 0,

ecuatia planului paralel cu axa Oz este: Ax + By + D = 0.

5) Ecuatia unui plan ce contine o axa de coordonate

De exemplu, planul ce contine axa Ox, deci trece prin origine, are ecuatia de forma:
By + Cz = 0.

Planul ce contine Oy are ecuatia: Ax + Cz = 0.

Planul ce contine Oz are ecuatia: Ax + By = 0.

2.2. Tipuri de ecuatii ale unui plan

Ecuatia unui plan ce trece prin M₀(x₀, y₀, z₀) si este perpendicular pe vectorul este:

.

Ecuatia unui plan ce trece printr-un punct M₀(x₀, y₀, z₀) si este paralel cu doua directii date, si este:

.

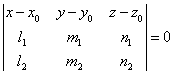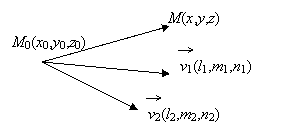
Într-adevar, daca M(x, y, z) apartine planului, atunci vectorii sunt coplanari, deci produsul mixt () = 0.

Rezulta: .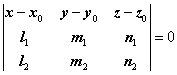

2. Ecuatia unui plan ce trece prin doua puncte M_i(x_i, y_i, z_i) i = 1,2 si este paralel cu o directie data este .

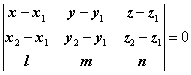Într-adevar, daca M(x, y, z) apartin planului, atunci vectorii sunt coplanari, deci produsul lor mixt = 0.

3. Ecuatia unui plan ce trece prin trei puncte necoliniare M_i(x_i, y_i, z_i) i = 1, 3. Se reduce la cazul 2, deci scriem ecuatia unui plan ce trece prin punctele M₁ si M₂ si este paralel cu . Daca M(x, y, z) apartine planului, atunci rezulta ca produsul mixt deoarece vectorii , sunt coplanari.

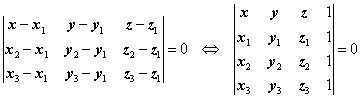
Caz particular

Fie M₁(a, 0, 0), M₂(0, b, 0), M₃(0, 0, c) puncte de intersectie cu axele de coordonate. Calculând, avem ecuatia ecuatia planului prin taieturi.

Aplicatia 1. Sa se scrie ecuatia planului care trece prin origine, prin punctul M₁(x₁, y₁, z₁) si este perpendicular pe planul (P) ax + by + cz + d = 0.

Solutie: Fie planul cautat (p) de ecuatie: AX + By + Cz + D = 0.

Întrucât planul (p):

trece prin origine, rezulta ca D = 0.

contine pe M₁, rezulta ca Ax₁ + By­₁ + Cz₁ = 0.

perpendicular pe planul (P), rezulta ca Aa + Bb + Cc = 0.

În aceste conditii obtinem: 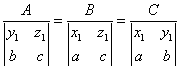ecuatia planului (p) este:

(cy₁ - bz₁)x + (az₁ - cz₁)y + (bx₁ - ay₁)z = 0.

2.3. Ecuatiile canonice ale unei drepte în spatiu

Propozitia 1. Fie M₀(x₀, y₀, z₀) punct fix, vectorul nenul si un punct oarecare M(x, y, z) apartinând dreptei d ce trece prin M₀ si este paralela cu Atunci coordonatele (x, y, z) ale punctului M verifica ecuatiile:

(ecuatiile canonice ale dreptei în spatiu).

Demonstratie: , , 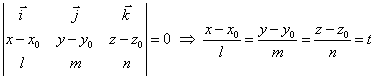t (parametru real).

Observatie.

Din

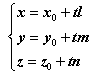, cu t , reprezinta ecuatiile parametrice ale dreptei.

2.4. Tipuri de ecuatii ale unei drepte în spatiu

1. Ecuatia dreptei ce trece prin doua puncte M_i(x_i, y_i, z_i), i = 1, 2.

Fie si M(x, y, z) punct oarecare pe dreapta M₁M₂.

Ţinând seama de Propozitia 1, 2.3, rezulta ca .

Aplicatia 1. Sa se scrie ecuatia dreptei care trece prin origine si prin punctul A(a, b, c).

Solutie:

sau x = at, y = bt, z = ct.

Aplicatia 2. Fie punctul M(a, b, c) si dreapta (d): .

Se cer:

a) Proiectia M' a punctului M pe dreapta (d);

b) Simetricul M'' al punctului M fata de (d);

c) Ecuatia unei drepte ce trece prin M si este perpendiculara pe (d) si intersecteaza planul (P).

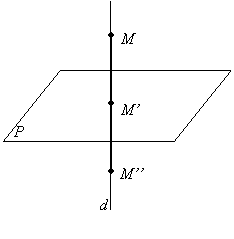
a) Dreapta (d) are vectorul director .

Avem de asemenea, ecuatiile parametrice ale dreptei (d): , t (1)

Scriem ecuatia unui plan (P) ce contine punctul M si este perpendicular pe (d):

l(x - a) + m(y - b) + n(z - c) = 0. (2)

Fie M'(x', y', x') punctul de intersectie al dreptei (d) cu planul (P): .

Aflam valoarea parametrului t înlocuind relatia (1) în relatia (2):

(3)

si în sfârsit coordonatele x', y', x' ale punctului M', proiectia punctului M , din relatia (1) folosind valorile parametrului t din relatia (3).

b) Fie M"(x", y", z") simetricul punctului M fata de (d).

Atunci, conform relatiei care da coordonatele mijlocului M' al unui segment în functie de coordonatele capetelor segmentului M si M'', avem:

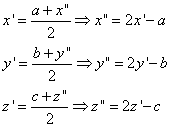
c) Dreapta trece prin M si M', are deci ecuatia:

2.5. Dreapta de intersectie a doua plane. Fascicol de plane

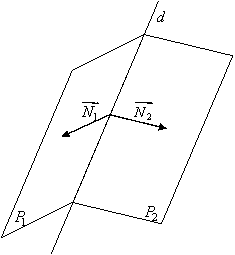
Fie doua plane neparalele. Ele se intersecteaza dupa o dreapta d, de ecuatie:

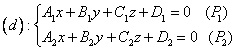
Ne propunem sa gasim ecuatiile canonice ale dreptei (d). Pentru aceasta alegem un punct M₀(x₀, y₀, z₀) d. Mai precis (x₀, y₀, z₀) este o solutie particulara a sistemului

.

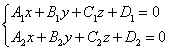Determinam directia dreptei d, , adica determinam l, m, n.

Scriem normalele la planele P₁ si P₂, adica:

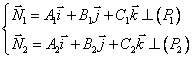
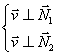
Dar , unde :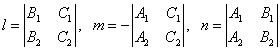

deci ecuatia dreptei este

,

cu l, m, n dati de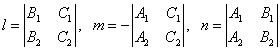

Fascicol de plane

Definitie. Se numeste fascicol de plane multimea tuturor planelor care contine o dreapta data (d).

Propozitie. Fie dreapta (d), intersectia planelor P₁ si P₂, adica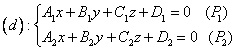

Planele nu sunt paralele, deci ecuatia unui plan ce apartine fascicolului de plane generat de dreapta (d) este:

(A₁x + B₁y + C₁z + D₁) + b( A₂x + B₂y + C₂z + D₂) = 0 cu b b

Daca = 1 si b = 0 rezulta A₁x + B₁y + C₁z + D₁ = 0 deci (P₁) este de forma enuntata.

Daca = 0, b = 1 rezulta A₂x + B₂y + C₂z + D₂ = 0 deci (P₂) este de forma enuntata si planul (P₁) + b(P₂) = 0 contine dreapta d.

Se poate arata ca fascicolul definit de dreapta d este de forma ₁P₁ + ₂P₂ = 0.

2.6. Probleme metrice

2.6.1. Distanta de la un punct la un plan

Propozitie: Fie Ax + By + Cz + D = 0 planul (P) si M₀(x₀, y₀, z₀), un punct care nu apartine planului (P). Atunci distanta de la punctul M₀ la planul (P) este:

Demonstratie: Fie M' (x', y', z') proiectia lui M₀ pe plan.

Deoarece este coliniar cu rezulta ca:

si mai departe

Atunci

Pe de alta parte (x', y', z') verifica ecuatia planului (P) deci:

2.6.2. Distanta de la un punct M₀ la o dreapta d în spatiu

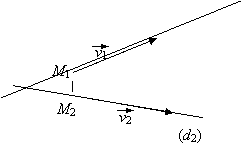
Propozitie: Fie dreapta (d), M₀ d, M₁(x₁, y₁, z₁) proiectia lui M₀(x₀, y₀, z₀) pe dreapta (d). Atunci distanta de la punctul M₀ la dreapta (d) este:

,

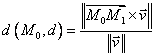unde este vectorul director al dreptei (d).

Demonstratie:

Daca proiectam punctul M₀ pe dreapta (d), obtinem:

2.6.3. Unghiul a doua plane

Definitie. Unghiul a doua plane este unghiul dintre normalele celor doua plane.

Fie ecuatiile planelor (P₁) si (P₂):

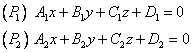
si fie ecuatiile normalelor lor:

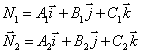
Atunci

Aplicatia 1. Sa se scrie unghiul dintre planele (P₁) si (P₂), date de ecuatiile:

(P₁) 2x - y + 3z + 2 = 0

(P₂) x + y - z + 5 = 0.

Aplicatia 2. Sa se gaseasca proiectia ortogonala a punctului M₀(x₀, y₀, z₀) pe dreapta:

.

Solutie

Consideram datele:

M

Proiectia M'(x', y', z') a punctului M₀ pe dreapta data se afla la intersectia dreptei (D) cu planul dus prin M₀ perpendicular pe D

Ecuatia planului în cazul nostru este 3(x - 5) + 2y + 4(z + 2) = 0 sau 3x + 2y + 4z - 7 = 0.

Înlocuim în aceasta ecuatie a planului ecuatiile parametrice ale dreptei (D) si obtinem valoarea parametrului real t.

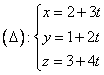29t + 13 = 0 .

Deci .

2.6.4. Distanta dintre doua drepte în spatiu

Fie dreptele:

Avem trei cazuri:

(d1)

1) Drepte concurente . Deoarece d₁ si d₂ sunt doua drepte concurente în acelasi plan rezulta ca distanta dintre ele este 0, atunci coplanare.

Drepte paralele . Dreptele sunt coplanare, deci putem scrie atunci distanta de la M₁ la dreapta d₂ ca în § 2.6.2.

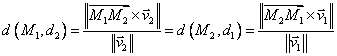
(d1)

3) Drepte oarecare în spatiu

(d2)

M2

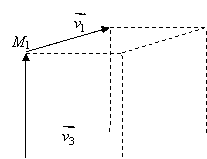
Distanta dintre d₁ si d₂ este lungimea perpendicularei comune celor doua drepte.

Perpendiculara comuna celor doua drepte este o dreapta perpendiculara si pe d₁ si pe d₂ si care intersecteaza dreptele d₁ si d₂.

Fie si vectorii directori ai dreptelor d₁ si d₂ , respectiv.

În punctul M₂ ducem un vector echipolent cu

Suporturile vectorilor si formeaza un plan. Rezulta ca dreapta d₁ este paralela cu acest plan.

Deci distanta dintre cele doua drepte este înaltimea paralelipipedului format de vectorii si

V_{paralelipiped} = = S_{bazei paralelipiped} · h_{paralelipiped}

Dar S_bazei = ;

Atunci h_{paralelipiped}=

Exercitii.

1) Sa se scrie ecuatia unui plan cunoscând P(2, 3, 4) unde P este piciorul perpendicularei (proiectia) punctului O(0, 0, 0) pe plan.

Solutie:

Ecuatia planului care trece prin punctual P(2,3,4) este:

,

unde A, B, C sunt parametrii directori ai normalei la plan,

.

În cazul nostru:

.

Ecuatia planului devine deci:

2) Se da dreapta d :

Sa se scrie ecuatia unui plan (P) ce contine drepta d si este perpendicular pe planul
(P_*) : x + y + z + 1900 = 0.

Solutie :

Planul (P) apartine fascicolului de plane determinat de dreapta d, adica:

, cu

Normala la planul (P) este deci :

Pe de alta parte, normala la planul (P_*)  este :

Dar

Introducând în ecuatia fascicolului obtinem ecuatia planului (P):

.

3) Se da dreapta (d) de ecuatii si M(-1, 2, 3). Sa se scrie ecuatia unui plan (P) ce trece prin punctul M si este perpendicular pe dreapta d.

Solutie :

Ecuatia planului cautat este de forma:

unde: x₀ = -1 , y₀ = 2, z₀ = 3 (punctul )

C = 1, B = 1, A = 3 (dreapta (d) este normala la planul (P)),

deci ecuatia planului devine :

, adica .

Probleme propuse.

Sa se scrie ecuatia dreptei ce trece prin punctul M₀(1, -1, 3) si este perpendiculara pe planul x + y + z + 3 = 0.

Sa se calculeze distanta de la punctul M(1, 1, 1) la planul 3x + y + z + 7 = 0.

3) Sa se rescrie ecuatiile dreptei care trece prin punctul (2, -5, 3) si este:

a) paralela cu axa Oz;

b) paralela cu dreapta

4) Sa se scrie ecuatia dreptei AB unde A(2, -1, 0), si sa se calculeze cosinii directori ai directiei determinate de dreapta AB.

5) Sa se scrie ecuatia dreptei care trece prin origine si prin punctul A(a, b, c).

6) Se considera dreapta determinata de punctele A(1, 2, 3), B(-2, 1, 4). Sa se gaseasca punctele ei de intersectie cu planele de coordonate.