Programare matematica cu mai mute functii obiectiv

PROGRAMARE MATEMATICA CU MAI MUTE FUNCTII OBIECTIV

7. SC. Santa S.A este o firma care produce medicamente si doreste sa determine reteta pentru un comprimat (compozit) cu anumite caracteristici biologice. Baza informationala este data in tabelul urmator:

Functiile obiectiv:

1.     Costul sa fie minim;

2.     Numarul de excipinti sa fie maxim;

3.     Cantitatile totale de medicament ce intra in ciclul de viata al unui comprimat sa fie minima.

Vom face urmatoarele notificari:

X1 – cantitatea din I1

X2 – cantitatea din I2

X3 – cantitatea din I3

X4 – cantitatea din I4

X5 – cantitatea din I5

X6 – cantitatea din I6

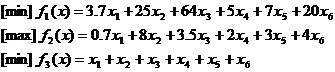
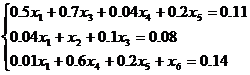
In vederea efectuarii calculelor vom folosi Programarea Liniara in QM.

Pasul 1: Introducerea conditiilor in QM

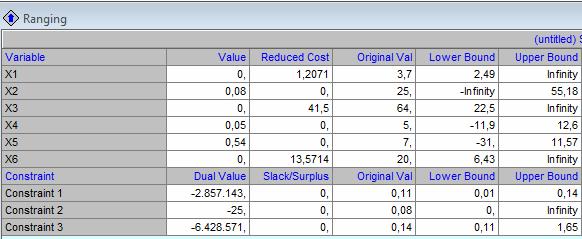
Datele introduse in QM pentru a afla Optimum 1 (O1) la min f1(x) sunt:

Pasul 2: Rezolvarea problemei cu ajutorul QM:

Rezolvarea in QM pentru a afla Pesimum 1 (P1):

Datele introduse in QM pentru a afla Optimum 2 (O2) la max f2(x) sunt:

Rezolvarea problemei cu ajutorul QM:

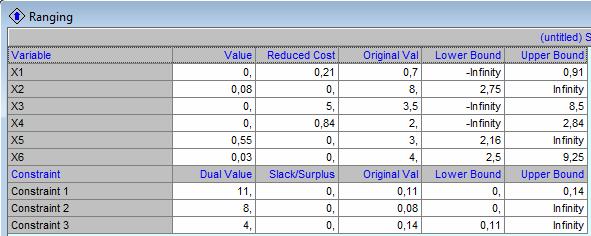
Rezolvare in QM pentru a afla Pesimum 2 (P2):

Datele introduse in QM pentru a afla Optimum 3 (O3) la min f3(x) sunt:

Rezolvarea problemei cu ajutorul QM:

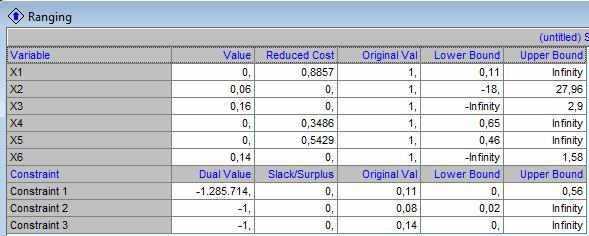
Rezolvare in QM pentru a afla Pesimum 3 (P3):

In urma calculelor efectuate au rezultat urmatoarele solutii:

α1 O1+β1 = U1                             α1 6.04+β1 = 1 α1= - 0.11

α1 P1+β1 = 1-U1    => α1 14.46+β1 = 0 => β1= 1.72

α2 O2+β2 = U2                             α2 2.41+β2 = 1 α2= 1.08

α2 P2+β2 = 1-U2    => α2 1.49+β2 = 0 => β2= - 1.62

α3 O3+β3 = U3                             α3 0.36+β3 = 1 α3= - 0.53

α3 P3+β3 = 1-U3    => α3 2.21+β3 = 0 => β3= 1.19

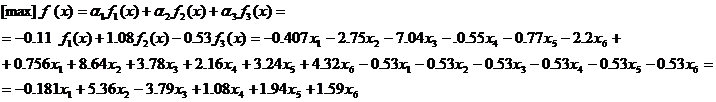
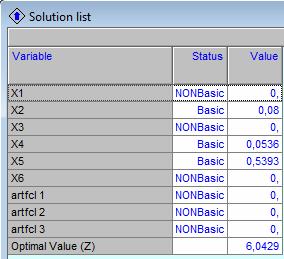
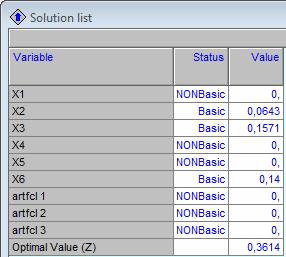
Datele introduse in QM pentru a afla solutiile functiei F(x) sunt:

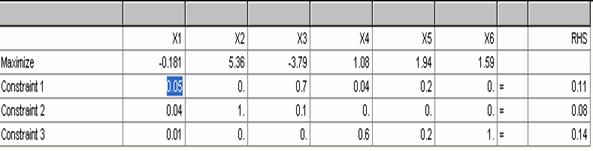
Rezolvarea problemei cu ajutorul QM:

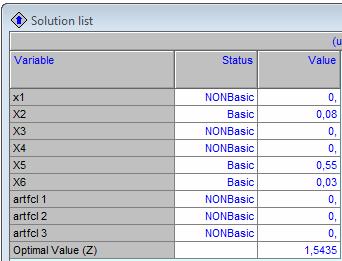
Solutiile sunt: X1 = 0; X2 = 0.08; X3= 0; X4= 0; X5= 0.55; X6= 0.03 si maximul functiei este 1.54.

1.54 + β1 + β2 + β3 = 1.54 + 1.72- 1.62 + 1.19 = 2.83

Conform literaturii de specialitate valoarea gradului de apartenenta trebuie sa fie maxim 3, in cazul nostru este 2.83.

MULTIMI VAGI (FUZZY)

1. Apple este singurul producator international al urmatoarelor 3 produse: Iphone (P1), Ipod (P2) si Laptopuri Mac si accesoriile sale (P3). Stabileste pentru perioada urmatoare structura de produse ce maximizeaza gradul de satisfacere simultana a obiectivelor:

A: Obtinerea unui venit cat mai mare sau aproape de 3200 (mii u.m),dar nu mai mic de 2900 (mii u.m.).

B: Suplimentarea unei cantitati cat mai reduse a disponibilului de resurse.

C: Realizarea productiei la nivelul cererii sau cat mai aproapede nivelul cererii.

Ipoteze:

a)     Cererea si pretulau fost determinate prin studii de marketing

b)     Resursele pot fi suplimentate cu maxim 650 u. f. Pentru fiecare.

c)     Cererea nesatisfacatoare trebuie sa fie mai mica de 75 u. f din fiecare varianta de produs.

Costurile specifice, cererea, resursele disponibile si preturile unitare sunt date mai jos:

5X1+3X2+10X3 ≤ 2900 + 300 => 5X1+3X2+10X3+300µ ≤ 3200

3X1+3X2+5X3 ≤ 1000 + 650 => 3X1+3X2+5X3+6500µ ≤ 1650

4X1+1X2+6X3 ≤ 900 + 650 => 4X1+1X2+6X3+650µ ≤ 1450

X1 ≥ 150 – 75 => X1 - 75µ ≥ 75

X2 ≥ 300 – 75 => X2 - 75µ ≥ 225

X3 ≥ 100 – 75 => X3 - 75µ ≥ 25

Functia de optimizat este urmatoarea: MAX (Z) = µ = 0.42

Astfel pornind de la calculele de mai sus vom avea urmatoarele conditii si restrictii:

5X1+3X2+10X3+300µ ≤ 3200

3X1+3X2+5X3+650µ ≤ 1650

4X1+X2+6X3+650µ ≤ 1450

X1 - 75µ ≥ 75

X2 - 75µ ≥ 225

X3 - 75µ ≥ 25

µ ≤ 1

X1,X2,X3,µ ≥ 0

In vederea efectuarii calculelor vom folosi Programarea Liniara in QM.

Pasul 1: Introducerea conditiilor in QM:

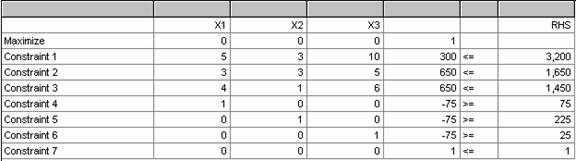
Pasul 2: Rezolvarea problemei cu ajutorul QM:

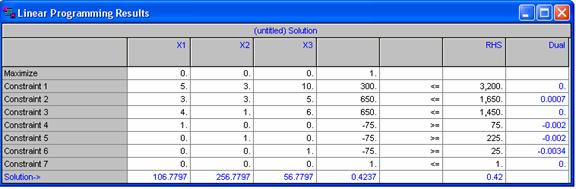
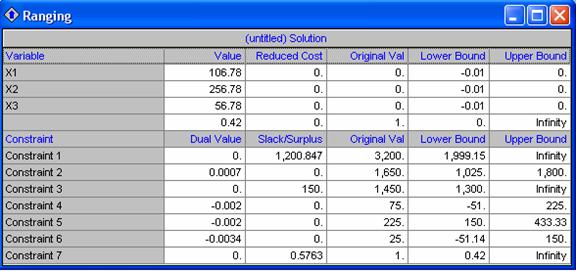
Potrivit programului rezultatele sunt urmatoarele:

X1 = 106.78 ; X2 = 256,78 ; X3 = 56,78 ; µ = 0,4237 ≈ 0,42

2. Un student doreste achizitionarea unui mouse in conformitate cu exigentele procesului tehnologic cu urmatoarele caracteristici:

C1: pret cat mai mic (u.m.)

C2: consum cat mai mic de timp la utilizare (secunde)

C3: cheltuieli cu intretinerea mici (lei)

C4: dimensiune mica (mp)

C5: consum mic de energie (u.f. de energie/u. timp)

Exista 6 oferte de mouse-uri care realizeaza operatia tehnologica dorita, dar avand fiecare alta caracteristica cu datele prezentate in tabelul de mai jos:

Pentru C1, C3, C4 si C5, care sunt functii de minim, se aplica formula g(x) = 1 – [ g(x) – nivel de aspiratie minim] / abaterea. De exemplu: pentru M1 formula de calcul este: 1- (11-8) / 5 = 0.4 si asa mai departe pentru restul calculelor.

Pentru C2, care este o functie de maxim, se aplica formula g(x) = 1 – [nivel de aspiratie maxim – g(x)] / abaterea. De exemplu: pentru M1 formula de calcul este: 1- (19-18) / 5 = 0.8 si asa mai departe pentru restul calculelor.

In urma calculelor efectuate avem urmatoarele rezultate: M1 = 0.25 ; M2 = 0.1 ; M3 = 0.1; M4 = 0.2 ; M5 = 0.1 ; M6 = 0.1 . Astfel mouse-ul care realizeaza operatia tehnologica dorita este : M1.