Recunoasterea formelor si interpretarea imaginilor

Recunoasterea formelor si interpretarea imaginilor

Unul dintre obiectivele cele mai ambitioase în analiza si interpretarea computerizata a imaginilor este acela de a construi sisteme capabile sa demonstreze diferite grade de inteligenta, care sa se apropie de comportamentul uman. Prin inteligenta întelegem: capacitatea de a extrage informatii pertinente dintr-un context ce contine numeroase detalii irelevante, capacitatea de a învata din exemple si a generaliza cunostintele obtinute la situatii noi si capacitatea de a face deductii corecte pe baza unor date incomplete sau imperfecte. Sisteme cu asemenea caracteristici au fost realizate pâna în prezent numai pentru un context de situatii posibile relativ limitat.

Obiectivul acestui capitol, îl constituie introducerea unor notiuni de baza din domeniul recunoasterii formelor, cu un accent special pe metodele de clasificare statistice, mai apropiate de materialul prezentat în capitolele anterioare. De asemenea, vom face o scurta introducere în problematica interpretarii imaginilor. Mai mentionam ca multe din rezultatele descrise aici sunt utile si în elaborarea unor metode de prelucrare de nivel inferior avansate.

În recunoasterea formelor, presupunem ca imaginea a fost preprocesata si segmentata si ca dispunem de descrieri adecvate ale regiunilor, capabile sa înglobeze informatiile necesare recunoasterii. Mai general, formele pot avea un caracter nevizual, daca ne referim, de exemplu, la recunoasterea vorbirii sau la prognoza valorii unei actiuni la bursa. Metodele de clasificare pot fi aceleasi, partea de prelucrare a informatiei cea mai specifica aplicatiei fiind cea care conduce la descriere. 

9.1. Procesul de recunoastere în abordarea statistica

9.1.1. Concepte de baza

În recunoasterea formelor prin metode statistice, orice forma este reprezentata cu ajutorul unui numar de descriptori scalari, grupati într-un vector. Un asemenea vector P-dimensional, x, denumit vector de forma defineste un punct în spatiul formelor. Rezolvarea unei aplicatii de recunoastere a formelor prin metode statistice presupune alegerea unui set de caracteristici adecvat pentru constructia vectorilor de forma si proiectarea unui clasificator, capabil sa atribuie orice forma, reprezentata cu ajutorul unui asemenea vector, unei clase, w_k, dintr-un numar finit de clase posibile, K. Recunoasterea formelor cuprinde doua etape: proiectarea clasificatorului, sau stabilirea regulilor de decizie si clasificarea propriu-zisa, adica folosirea clasificatorului.

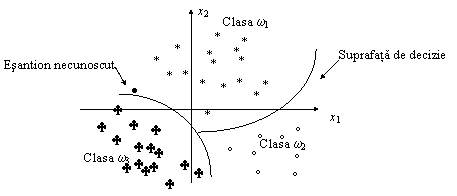
Fig. 9.1. Exemplu de recunoastere de forma cu trei clase într-un spatiu al proprietatilor bidimensional

Proiectarea clasificatorului poate fi formulata ca o problema a partitionarii spatiului caracteristicilor între clasele posibile. O reprezentare geometrica intuitiva pentru o problema de clasificare cu P = 2 si K = 3 se da în Fig. 9.1. Simbolurile reprezentate în figura sunt esantioane etichetate, a caror apartenenta la clase este cunoscuta, în urma unei clasificari manuale. Aceste esantioane, denumite de învatare sau de antrenament, concentreaza informatiile specifice aplicatiei, pe baza carora se proiecteaza clasificatorul. Mentionam ca este exista si aplicatii în care asemenea esantioane nu sunt disponibile si clasificatorul trebuie sa învete singur, pe baza datelor ce urmeaza a fi clasificate. Proiectarea clasificatorului pe baza esantioanelor de antrenament este denumita învatare, instruire sau antrenament si are ca rezultat partitionarea spatiului formelor. În Fig. 9.1, domeniile apartinând diferitelor clase sunt delimitate cu ajutorul unor curbe. Într-un spatiu tridimensional, am fi avut nevoie de niste suprafete pentru a face acelasi lucru. Pentru spatii cu mai mult de trei dimensiuni, nu mai exista interpretare geometrica intuitiva, dar se pastreaza denumirea de suprafata de decizie (hipersuprafata) pentru multimea punctelor ce separa clase diferite.

Fig. 9.2. Strategii de recunoastere: a) învatare înaintea recunoasterii,

b) învatare si recunoastere concomitenta

Presupunând o problema de clasificare cu K clase, w w w_K si o reprezentare a formelor cu ajutorul vectorilor de forma P dimensionali, x = [x₁, x₂,..., x_P]^T, proiectarea clasificatorului consta în a se gasi K functii de decizie, sau functii discriminant, d₁(x), d₂(x),...,d_K(x), astfel încât:

" x w_i , d_i(x) > d_j(x) , j = 1,2,...,K; j i

O data gasite aceste functii, clasificarea poate decurge în felul urmator. Vectorul necunoscut, supus clasificarii, este prezentat ca argument la intrarea fiecarei functii discriminant. Regula de decizie este urmatoarea: vectorul apartine clasei a carei functii discriminant are valoarea maxima. Cazurile de egalitate se rezolva arbitrar. Ecuatiile de forma

d_i(x) d_j(x),   (9.2)

sau, echivalent,

d_ij(x) d_i(x) d_j(x) = 0,  (9.3)

definesc suprafetele de decizie dintre clasele i si j.

Dupa ce clasificatorul a fost proiectat, este posibila recunoasterea unor forme noi, pe baza regulilor de decizie stabilite în prima faza. Schema bloc a unui sistem de recunoastere de forme cu învatare înainte de recunoastere este redata în Fig. 9.2a. Aici regulile de decizie gasite în faza de învatare ramân fixe pe parcursul operatiei de recunoastere. O strategie alternativa este prezentata în Fig. 9.2b. Sistemul are reactie, este adaptiv si învata secvential, pe masura ce la intrare sunt aduse noi esantioane. Este presupusa existenta detectorului de eroare (învatatorul) pe parcursul recunoasterii, pentru a furniza reactia. Un asemenea sistem se poate adapta la modificari ale statisticii procesului. Cel mai frecvent însa învatatorul este disponibil doar în faza de antrenament si un asemenea sistem lucreaza tot cu reguli de decizie fixe. În acest caz, distinctia dintre cele doua sisteme devine neesentiala. Este posibila totusi adaptarea si în absenta învatatorului. Clasificarea unui esantion este considerata aprioric corecta si acesta este folosit apoi pentru modificarea suprafetelor de decizie. O asemenea strategie poate fi necesara în cazul aplicatiilor ale caror caracteristici sunt susceptibile sa se modifice în timp. La un asemenea sistem adaptiv, regulile de decizie sunt influentate mai puternic de esantioanele recente, efectul esantioanelor mai vechi fiind uitat" treptat.

9.1.2. Clasificatorul de distanta minima

Clasificatorul de distanta minima presupune determinarea unui vector de forma prototip pentru fiecare clasa. Uzual, prototipul fiecarei clase este definit ca vector mediu al esantioanelor de antrenament ce apartin clasei respective.Fie ^jx_n vectorii de antrenament ai clasei j, cu n = 1,2,...,N_j. Vectorul mediu al clasei j este:

. (9.4)

Pentru versiunea secventiala, vectorul mediu se poate calcula recursiv:

. (9.5)

Vectorul mediu sau prototipul clasei j astfel definit este centroidul punctelor din spatiul formelor ce apartin clasei respective. Clasificatorul de distanta minima atribuie un vector necunoscut, x, clasei j pentru care distanta

(9.6)

este minima. Pentru ca

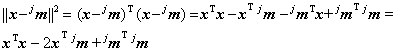
si pentru ca primul termen al sumei de mai sus nu depinde de indicele de clasa, criteriul este echivalent cu maximizarea functiei discriminant

. (9.7)

Se recunoaste usor ca avem de fapt de-a face cu o metoda de intrecorelatie. Primul termen reprezinta intrecorelatia dintre vectorul necunoscut si prototipul clasei j. Al doilea termen reprezinta energia prototipului, exceptând factorul 1 . Acest termen poate fi stocat în memoria clasificatorului, astfel ca în momentul clasificarii ramâne de calculat un singur produs intern si o scadere, ceea ce este mai rapid decât calculul efectiv al distantei cu ajutorul ecuatiei (9.6). Ecuatia suprafetei de decizie pentru clasificatorul de distanta minima ia forma

(9.8)

Suprafata definita de ecuatia (9.8) este perpendiculara pe dreapta ce uneste punctele ⁱm si ^jm pe care o intersecteaza la jumatatea distantei dintre cele doua puncte. În cazul unui spatiu al formelor bidimensional, suprafata se reduce la o dreapta. Daca spatiul este tridimensional, suprafata este un plan, iar pentru dimensiuni ale spatiului, P > 3, vom denumi aceasta suprafata hiperplan

Exemplu: Fie vectorii prototip bidimensionali, m si m [3, 3] din Fig. 9.3. Functiile discriminant sunt d (x) = x^{T 1}m 0.5¹m^{T 1}m = 2x₁ + x₂ si d (x) = x^{T 2}m 0.5²m^{T 2}m = 3x₁ + 3x₂ Ecuatia frontierei dintre cele doua regiuni este: d (x) = d₁(x) d₂(x) = x₁ 2x₂ + 6.5 = 0.

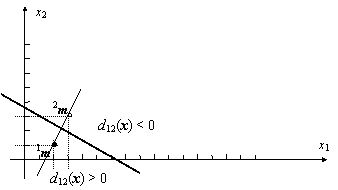
Fig. 9.3. Dreapta de decizie pentru un clasificator de distanta minima în spatiul bidimensional, cu doua clase

9.1.3. Probleme ascunse

Interpretarea geometrica a procesului de recunoastere a formelor prin metode statistice si solutia oferita de clasificatorul de distanta minima pot conduce la impresia ca problema este deceptionant de simpla. În realitate, exista numeroase probleme ascunse, ce trebuiesc tratate cu atentie.

Normalizarea

Clasificatorul de distanta minima foloseste distanta euclidiana pentru a decide daca un vector de forma este mai plauzibil sa apartina unei anumite clase sau alteia. Procedând în acest mod, se poate trece usor cu vederea faptul ca în recunoasterea formelor componentele vectorului de forma au semnificatii fizice diverse ( adunam mere cu pere"). Ceea ce poate deveni de fapt o problema este ordinul de marime, adesea foarte diferit, al marimilor ce intervin. De exemplu, daca x (x₁, x₂) si x reprezinta factorul de forma al unei regiuni, ce ia valori între 0 si 1, în timp ce x reprezinta aria regiunii si poate lua valori între 1 (putin probabil) si 50.000, devine usor de anticipat ca x are un rol neglijabil în luarea deciziilor. De exemplu, daca prototipurile a doua clase sunt m si m , pentru vectorul x se obtin distantele D (x) = (0 + 100²) = 10000 si D (x) = (0.7² + 90² ) = 8100.49. Clasificatorul de distanta minima decide pentru clasa w , practic excusiv pe criteriul ariei, cu toate ca aria de 2100 este aproximativ la fel de îndepartata de valorile tipice ale ambelor regiuni, în timp ce factorul de forma pare sa indice o apartenenta clara la regiunea w . Pentru a face variabila x sa aiba o pondere asemanatoare cu cea a variabilei x la calculul distantei, este necesar sa normalizam spatiul deciziilor înainte de antrenarea clasificatorului. Normalizarea conduce la un spatiu al formelor mai "patrat". O solutie posibila este pe baza amplitudinii axelor, definite prin:

(9.9)

Amplitudinea a_p se determina pentru fiecare proprietate, x_p, din componenta vectorului de forma si foloseste esantioanele de antrenament ale tuturor claselor. Normalizarea consta în raportarea proprietatilor x_p la amplitudine:

x_p x_p / a_p (9.10)

Procedura este simpla dar sensibila la zgomot, datorita operatiilor de calcul de extrem. O varianta de normalizare mai robusta consta în raportarea la deviatia standard pe fiecare axa,

x_p x_p / s_p (9.11)

unde

, (9.12)

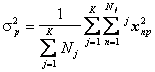. (9.13)

Normalizarea este o operatie necesara, dar nu poate rezolva complet problema esentiala, a generarii unui spatiu al formelor în care distanta dintre esantioane sa corespunda perfect cu similaritatea formelor.

Metrici

Distanta euclidiana este o masura a similaritatii convenabila prin faptul ca este o marime usor derivabila, ale carei maxime sau minime se pot afla rezolvând ecuatii liniare. Cu toate acestea, nu exista nici o garantie în privinta faptului ca ea reprezinta cea mai buna masura pentru ceea ce ne intereseaza de fapt: similaritatea formelor. Pentru a sublinia generalitatea discutiei, vom lua un exemplu de aplicatie din afara domeniului prelucrarii imaginilor. Sa presupunem ca vrem sa evaluam riscul de producere al unui accident rutier de catre un vehicul printr-o tehnica de recunoastere de forma. Pentru simplitatea exemplului, folosim numai doua proprietati: viteza de deplasare si timpul la volan al conducatorului auto. Intuitiv este evident ca riscul de producere al unui accident la cresterea vitezei de la 10 km/h la 40km/h este considerabil mai mic decât cel provocat de cresterea vitezei de la 90 km/h la 120km/h. De asemenea, cresterea timpului la volan de la 1 ora la 2 ore are un efect considerabil mai mic decât cresterea lui de la 21 de ore la 22 de ore. Simpla normalizare nu rezolva asemenea probleme. Solutii mai bune pot rezulta folosind metrici diferite de cea euclidiana. Daca putem aprecia valoarea fiecarei proprietati din componenta vectorului de forma în clasificare, o transormare diagonala de forma

x = W x

cu

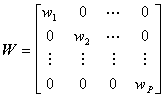(9.15)

si

(9.16)

permite o clasificare mai buna cu metrica euclidiana conventionala. Transformari neliniare adecvate ale axelor pot conduce, de asemenea, la caracteristici modificate si vectori de forma noi, a caror similitudine poate fi apoi corect evaluata prin distanta euclidiana sau alte metrici mai simplu de implementat, de genul sumei modulelor. Din punct de vedere practic, este important sa reperam situatiile în care problemele de metrica apar si sa luam masurile ce se impun.

Dimensionalitatea

Experienta cotidiana ne familiarizeaza cu spatiile de dimensiuni reduse (1,2 sau 3). Intuitia tinde sa nu ne mai fie de mare ajutor cînd dimensiunile spatiului se extind. Sa presupunem ca avem pe fiecare axa variabile cuantizate pe un octet. În spatiul unidimensional cuantizat exista 256 de puncte. Pentru cel bidimensional avem 256² = 65 526 de puncte. Pentru cel tridimensional, sunt 256³ 16 000 000 de puncte. Ce se întîmpla pentru o valoare "modesta" de spatiu cu 10 dimensiuni rezultat prin folosirea unui set de 10 descriptori Numarul de puncte este de aproximativ 10²⁴ = 1 000 000 000 000 000 000 000 000.

Pentru a întelege mai usor ce consecinte are cresterea dimensiunii spatiului asupra preciziei clasificatorului, este util sa privim Fig. 9.1 si sa concepem clasificarea ca o problema de interpolare. Pe baza unui set de esantioane cu apartenenta la clasa cunoscuta finit, ce ocupa un anumit procent (de regula modest) din spatiul formelor, este necesar sa stabilim carei clase apartine fiecare punct al spatiului. Prin pasul pe care-l facem la proiectarea clasificatorului, suntem fortati sa folosim inductia pentru a generaliza certitudinile noastre referitoare la esantioane asupra întregului spatiu al formelor. Riscul de a comite greseli este cu atât mai mare, cu cât esantioanele de antrenament ocupa un procent mai mic din spatiul formelor. Acest risc pare sa creasca vertiginos prin adaugarea fiecarei dimensiuni suplimentare spatiului formelor.

Experimente sistematice [Foley 1972] au condus la concluzia ca raportul N_j/P dintre numarul de esantioane ale fiecarei clase si dimensiunea spatiului formelor trebuie sa fie superior valorii de 3 5 pentru ca rata de eroare pe setul esantioanelor de antrenament sa fie apropiata de valoarea erorii pe date reale, în conditiile în care distribitiile statistice ale esantioanelor sunt cunoscute. În caz contrar, rapoarte mai mari decât cele indicate sunt necesare.

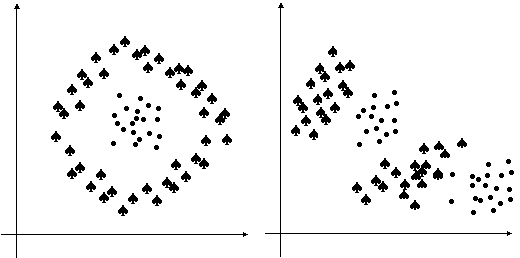
Fig. 9.4. Exemplu de distributii complexe

Distributii complexe

Adesea, esantioanele nu sunt distribuite regulat, sub forma unor nori, concentrati în jurul unui nucleu. Cu alte cuvinte avem de-a face cu distributii multimodale. Daca proprietatile folosite nu sunt statistic independente, distributiile multidimensionale tind sa aiba mai degraba aspectul unor fâsii. Daca dimensiunea spatiului formelor, P, este mai mare decât cea necesara, datele sunt distribuite pe o "suprafata" de dimensiune P < P. În concluzie, putem sa ne asteptam la forme ale distributiilor dintre cele mai diverse, conform exemplelor din Fig. 9.4.

O consecinta practica pe care o putem deduce din exemplele prezentate este aceea ca este posibil sa avem nevoie de suprafete de decizie de forme mai complicate. În particular, un clasificator de distanta minima de tipul introdus ar functiona cu rezultate catastrofale pe asemenea distributii (având în vedere unde vor fi situati centroizii celor doua clase).

Lotul de antrenament si lotul de testare

Performantele unui sistem pentru recunoasterea formelor sunt evaluate uzual prin rata erorii, reprezentând procentul de forme clasificate gresit. Ca si învatarea, verificarea presupune existenta unor esantioane preclasificate, astfel încât putem fi tentati sa refolosim esantioanele de antrenament pentru testarea performantelor. Din pacate, o asemenea procedura este cu totul neconcludenta, reprezentând o greseala flagranta. De altfel, unele tipuri de clasificator (de exemplu clasificatorul kNN) vor da întotdeauna eroare nula la reluarea testului pe lotul esantioanelor de antrenament. Examinam în continuare alte doua posibilitati.

Prima metoda consta în împartirea esantioanelor în doua parti egale. Primul lot se foloseste pentru deducerea regulilor de decizie, al doilea pentru testarea performantelor. Obiectia care i se aduce acestei proceduri este aceea ca risipeste esantioane valoroase, obtinute de regula cu multa truda, pentru verificare, când acestea ar putea fi folosite pentru a îmbunatati precizia clasificatorului. Se poate totusi face acest lucru ulterior, daca testul este satisfacator, cu certitudinea ca performantele nu pot decât sa creasca, dar trebuie sa recunoastem faptul ca acest lucru nu înlatura total obiectia formulata. Putem sa încercam o împartire inegala a esantioanelor, în favoarea celor destinate învatarii, ceea ce ne duce cu gândul la o întrebare pe care era bine sa ne-o punem în momentul deciziei de a diviza esantioanele în doua loturi. Câte esantioane sunt necesare pentru testarea performantelor Problema a fost studiata în [Highleyman 1962]. Concluzia lui este ca pentru o evaluare cu totul orientativa, sunt necesare esantioane de test de ordinul sutelor.

A doua metoda ( leave one out ) propune folosirea tuturor esantioanelor, cu exceptia unuia singur pentru antrenarea clasificatorului. Esantionul ramas este folosit pentru testarea performantelor. Nu va grabiti sa criticati metoda, înca nu s-a terminat. Esantionul folosit pentru testare este apoi reintrodus în lotul de antrenament. În locul lui este extras un alt esantion pentru testare si cu noul lot se repeta antrenamentul, apoi se reface testul pe esantionul extras si asa mai departe, pâna când fiecare esantion ajunge sa fie folosit si la testare. Ramâne sa se aleaga o varianta de reguli de decizie din multitudinea solutiilor generate, cu observatia ca nu exista recomandari interesante în acest sens. La un clasificator de calitate, regulile de decizie obtinute în diferite faze oricum nu difera semnificativ. Pe de alta parte, dupa terminarea testelor, se poate face un antrenament final cu lotul complet.

O problema adesea subestimata este reprezentativitatea loturilor de antrenament si de testare. Prin procesul de învatare, clasificatorul îsi adapteaza deciziile în functie de pozitiile esantioanelor preclasificate de care dispune. Una din metodele posibile pentru generarea regulilor de decizie, clasificatorul de distanta minima, a fost deja introdusa. Pentru ca sistemul sa se comporte la functionarea reala conform asteptarilor bazate pe rezultatele testelor, este necesar ca loturile finite ale esantioanelor de antrenament si de testare sa acopere cât mai complet întreaga varietate a formelor ce pot apare pe parcursul exploatarii acestuia. În acest sens, selectia formelor utilizate la antrenarea si testarea sistemului trebuie facuta cu mult discernamânt.

9.2. Selectia proprietatilor

Experienta arata ca aspectul cel mai important în rezolvarea cu succes a unei aplicatii de recunoastere a formelor îl reprezinta selectia proprietatilor, respectiv a descriptorilor. Nici un clasificator, oricât de sofisticat nu va fi în stare sa salveze o aplicatie de recunoastere de forme ce foloseste caracteristici proaste. În Capitolul 8, s-au discutat unele criterii ce pot servi la constructia unor descriptori de forma performanti. De exemplu, un descriptor robust este invariant la o serie de factori de influenta nedoriti. Am mentionat si faptul ca alegerea descriptorilor este o problema puternic dependenta de aplicatie, în care experienta si intuitia proiectantului au un rol esential, care, în prezent, nu poate fi substituit complet de nici un instrument teoretic. Presupunând însa ca dispunem de un set de caracteristici plauzibile extins, putem discuta modalitati de a obtine un set mai restrâns cu performante optime.

Aparent, cu cât mai mare numarul descriptorilor, cu atât mai bine. Din perspectiva proiectantului unui clasificator de forme însa, este importanta mentinerea dimensiunii spatiului formelor la valori moderate. Un set de caracteristici bune produce distributii ale esantioanelor în spatiul formelor grupate strâns în jurul unui prototip" pentru fiecare clasa. Totodata, prototipurile sunt separate prin distante mari în spatiul formelor, astfel încât distributiile claselor sa nu se întrepatrunda. Prima conditie poate fi evaluata cantitativ prin dispersia esantioanelor în interiorul fiecarei clase, ce trebuie sa fie cât mai mica. Cea de-a doua conditie cere ca dispersia interclasa a esantioanelor sa fie cât mai mare.

În principiu, putem afla valoarea unei caracteristici experimental, comparând rezultatele clasificarii cu ea si în absenta ei. Sa presupunem ca dispunem de 100 de caracteristici potential utile, din care vrem sa retinem 10. Solutia exhaustiva este sa formam toate cele 17.310.309.000.000 grupe de 10 caracteristici cu care sa experimentam proiectarea si functionarea clasificatorului. Evident, cautarea exhaustiva este prohibitiva în acest caz.

Aparent, putem forma un set de caracteristici bune alegând primele n caracteristici din setul de N, în ordinea performantelor de clasificare individuale ale fiecareia. Experimentele însa au condus la constatarea ca acest set nu este optimal [Cover 1974], ba chiar, în mod consternant, uneori alegerea sugerata a condus la rezultate dintre cele mai slabe, din toate variantele posibile. O procedura de selectie a caracteristicilor mai buna este de a se porni cu prima caracteristica în ordinea performantelor individuale, apoi sa se caute perechea de caracteristici optima, prin adaugarea unei alte caracteristici, continuând în acest mod secvential pâna la atingerea performantilor de clasificare dorite [Mucciardi 1971]. Alternativ, putem porni cu setul întreg de caracteristici si elimina la fiecare pas câte o singura caracteristica.

Motivul comportarii slabe a "echipei elitelor" poate fi acela ca toate caracteristicile selectate tind sa concentreze aproximativ acelasi tip de informatie. Transformarile ortogonale pot fi folosite pentru obtinerea unei submultimi de caracteristici mai putin corelate sau, în cazul transformarii Karhunen-Loeve, complet decorelate. Matricea de autocovarianta a vectorilor transformati devine diagonala si contine dispersiile vectorilor în spatiul transformat. Sa presupunem în extremis ca vectorii de forma contin doua caracteristici identice. Ele vor genera doua linii si doua coloane identice în matricea de covarianta, astfel ca rezulta cel putin o valoare proprie nula, respectiv o dispersie nula. Ea corespunde vectorului diferenta a celor doua caracteristici identice. Caracteristici similare, dar nu identice, vor conduce la coeficienti cu dispersii nenule dar foarte mici. Utilitatea lor în clasificare este redusa, astfel încât acestia pot fi eliminati fara a se schimba radical informatia continuta în setul de vectori ramas de dimensiuni reduse. Fiecare coeficient al transformarii din componenta noilor vectori de forma reprezinta o combinatie liniara a caracteristicilor din componenta vectorilor de forma initiali. Evident, clasificatorul bazat setul de caracteristici restrâns nu are performante mai bune, dar le poate avea apropiate. Ceea ce se câstiga în fond este faptul ca dimensiunea spatiului formelor se reduce.

9.3. Clasificatorul statistic optimal

Clasificarea formelor se confrunta cu o problema în care numerosi factori interactioneaza într-un mod complex, producând efecte cu aspect aleator. Este firesc, prin urmare, sa abordam clasificarea folosind instrumente de lucru statistice. Vom arata ca este posibila constructia unui clasificator statistic optimal, în sensul ca, în medie, comite cele mai putine erori de clasificare, sau, mai general, minimizeaza consecintele negative ale erorilor comise. 

Notam cu p(w_k|x) probabilitatea ca o forma x sa apartina clasei w_k. Decizia eronata pentru clasa w_k în situatia în care forma apartine clasei w_j atrage un cost, sau o pierdere, pe care o notam cu L_jk. În general nu toate deciziile eronate au costuri egale. De exemplu, daca un sistem de recunoastere de forme trebuie sa detecteze o situatie de avarie la o centrala termoelectrica nucleara, costul unei alarme false este considerabil mai mic decât cel al nesemnalarii unei situatii de avarie reale. În particular, L_jj este costul unei decizii corecte, ce uzual este evaluat la zero, pentru simplitate. Costul mediu sau riscul mediu conditionat al deciziei de clasificare a formei x într-o clasa w_k din cele K clase posibile este:

.

Folosind binecunoscuta egalitatea din teoria probabilitatilor, p(a b) = p(a|b) p(b) = p(b|a) p(a), ecuatia devine:

. (9.18)

Pentru ca factorul din fata sumei este pozitiv si nu depinde de indicele de clasa, el nu afecteaza relatia de ordine între riscurile conditionate de clasa si ca atare poate fi omis. Ecuatia se reduce la:

. (9.19)

Clasificatorul statistic optimal, cunoscut din teoria deciziilor sub denumirea de regula de decizie a lui Bayes, decide sa atribuie forma x pentru clasa cu riscul exprimat de ecuatia (9.19) este minim. Când costurile deciziilor pentru fiecare clasa sunt egale,

L_jk d_jk (9.20)

unde d_jk = 0 pentru j k d_jk = 1 pentru j = k, este simbolul Kronecker. În aceste conditii, riscul conditionat devine

(9.21)

Din nou p(x) nu influenteaza decizia, ce se face pentru clasa w_k pentru care

este maxim. Pentru ca 

, (9.23)

în forma (9.18), clasificatorul maximizeaza, de fapt, probabilitatea a posteriori ca forma x sa apartina clasei w_k.. Ecuatia (9.22) defineste functiile discriminant folosite pentru aplicarea regulii de decizie a lui Bayes în probleme cu costuri uniforme.

Probabilitatile apriorice de apartenenta la clasa, p(w_k) se pot estima relativ usor, cunoscând aplicatia. Ele reprezinta frecventele de aparitie ale claselor. Despre probabilitatile apriorice conditionate sau marginale, p(x|w_k), nu putem afirma însa acelasi lucru. Este vorba de estimarea unei distributii de probabilitate multidimensionala. În principiu, estimarea se poate face folosind esantioanele din lotul de învatare, cu apartenenta la clase specificata. Dificultatile provin din caracterul multidimensional, ce reclama un numar de esantioane exponential crescator cu dimensiunea vectorilor de forma, precum si din faptul ca legea de distributie este de cele mai multe ori necunoscuta. 

Clasificatorul Bayes de maxima verosimilitate pentru distributia gaussiana

În majoritatea covârsitoare a aplicatiilor ce folosesc clasificatorul Bayes, se face presupunerea ca legea de distributie a esantioanelor este cunoscuta, cu exceptia unor parametri ce urmeaza a fi estimati. O asemenea procedura conduce la o metoda de clasificare parametrica. Tot în majoritatea cvasiexclusiva a cazurilor, legea de distributie presupusa este gaussiana:

, (9.24)

unde ^jm este media clasei w_j si K_j este matricea de covarianta a clasei w_j. Media clasei poate fi estimata folosind ecuatia (9.3) sau (9.4). Pentru matricea de covarianta a clasei w_j, putem folosi ecuatia:

(9.25)

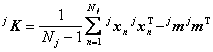
sau, în varianta recursiva,

. (9.26)

Pentru aplicarea regulii de decizie a lui Bayes formam o functie discriminant echivalenta prin logaritmarea ecuatiei (9.22), pentru a evita operatia de exponentiere. Logaritmul este o functie monotona, deci nu schimba relatia de ordine. Obtinem:

.

Eliminând termenii constanti în raport cu indicele de clasa, functia discriminant devine

. (9.28)

Suprafetele de decizie sunt denumite hipercuadrice, pentru ca nu apar termeni în x cu grad mai mare decât 2. O consecinta a acestui fapt este ca suprafetele de decizie la clasificatorul Bayes pentru distributii gaussiene pot lua doar forme relativ regulate. Optimalitatea se poate obtine totusi, dar numai în situatiile în care datele reale sunt modelate precis de distributia gaussiana. 

Daca probabilitatile apriorice ale claselor, p(w_j), sunt egale si matricile de covarianta ale tuturor claselor sunt egale cu matricea unitate (ceea ce presupune proprietati complet decorelate !), criteriul Bayes se reduce la

,

ceea ce se recunoaste a fi functia discriminant a unui clasificator de distanta minima. Asadar, clasificatorul de distanta minima este optim în sens bayesian numai în conditii restrictive ce arareori pot fi îndeplinite în practica.

9.5. Metode de clasificare neparametrice

Clasificatorul kNN

În pofida optimalitatii sale teoretice, clasificatorul Bayes ramâne adesea mai degraba un instrument teoretic, folosit pentru evaluarea comparativa performantelor unor metode de clasificare suboptimale. Comparatia se face pe date cu distributii cunoscute, care pun clasificatorul Bayes în situatie favorabila. Pornind de la observatia ca toate informatiile statistice de care dispunem referitor la problema de recunoastere provin din esantioanele preclasificate, o serie de metode de recunoastere, denumite neparametrice, încearca sa foloseasca aceste informatii pentru proiectarea clasificatorului direct, fara a mai încerca estimarea distributiilor de probabilitate multidimensionale. Un asemenea exemplu este chiar clasificatorul de distanta minima. Pentru ca singura informatie statistica exploatata de algoritm este momentul de ordinul întîi sau media, performantele sale sunt modeste, ceea ce nu excude folosirea lui în unele probleme, cu avantajul incontestabil al simplitatii.

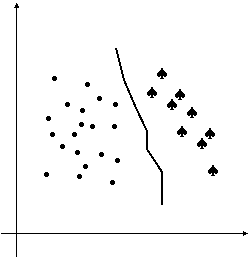
Fig. 9.5. Suprafata de decizie a unui clasificator NN

Interpretarea geometrica a problemei clasificarii sugereaza urmatoarea regula de decizie: atribuie fiecare forma la clasa al carei esantion preclasificat este cel mai apropiat. Metoda de clasificare propusa este denumita regula de decizie a vecinului celui mai apropiat. Pe scurt, NN de la "nearest neighbour". Clasificatorul NN poate fi conceput ca o generalizare a clasificatorului de distanta minima, în care fiecare clasa este reprezentata de toate esantioanele preclasificate disponibile, considerati vectori prototip ai clasei. Suprafetele de decizie ale pot avea forme complexe, fiind liniare pe potiuni (Fig. 9.5) pentru forme bidimensionale respectiv planare pe portiuni pentru suprafete de dimensiuni superioare. Mai general, regula de decizie se poate construi folosind k esantioane:

determina cei mai apropiati k vecini

decide pentru clasa care are cei mai multi reprezentanti între cei k vecini (vot majoritar);

daca doua sau mai multe clase au acelasi numar de reprezentanti, decide pe baza celui mai apropiat vecin.

În practica se folosesc pentru k valori reduse, valoarea k = 3 fiind arareori depasita, pentru ca nu aduce îmbunatatiri ale performantelor clasificatorului. Exista si variante ce pondereaza la vot clasele selectate în lotul celor k vecini în functie de distanta pâna la forma pentru care se face decizia. Din nou, câstigul în performanta este modest si se pierde avantajul simplitatii de baza a algoritmului. Indiferent însa de forma distributiei, eroarea nu depaseste dublul erorii produse de clasificatorul optimal, ceea ce poate fi considerata o performanta buna. De remarcat ca acest tip de clasificator nu are nevoie de antrenament.

x

x

a

b

c

Fig. 9.6. Suprafete de decizie paralele cu axele spatiului formelor

Principala critica adusa clasificatorului kNN este aceea ca necesita pentru fiecare decizie calculul distantelor la toate esantioanele preclasificate existente, ceea ce poate afecta suparator viteza de clasificare. Exista însa si solutii rapide, ce evita un calcul exhaustiv.

O solutie posibila este de a restrictiona suprafetele de decizie sa fie paralele cu axele spatiului formelor. Un exemplu bidimensional se da în Fig. 9.6. Regulile de decizie pentru o asemenea partitie se pot exprima eficient sub forma unui arbore binar. Exemplul din Fig. 9.7 se explica singur.

x a

x a

x c

x b

x c

START

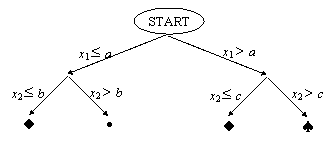
Fig. 9.7. Functie de decizie implementata sub forma unui arbore binar

Reducerea complexitatii de calcul (si a memoriei necesare pentru clasificator) se poate obtine si prin tehnici de condensare Hart 1968 , care cauta sa defineasca pentru fiecare clasa o submultime de esantioane preclasificate care asigura performante apropiate cu cel initial. Examinând Fig. 9.5, se observa ca majoritatea esantioanelor ar putea fi eliminata fara a se schimba forma suprafetei de decizie. În practica, selectia se poate realiza, de exemplu cu o metoda de tipul "live one out". Se încearca succesiv eliminarea unui esantion si se verifica performantele de clasificare ale subsetului ramas, folosind lotul esantioanelor de test. Practica adoptata curent este de a se elimina esantionul numai daca performantele de clasificare nu se modifica prin aceasta operatie.

Metoda functiilor potential

Asa cum sugereaza denumirea metodei, densitatea de probabilitate ca un punct, x, al spatiului formelor sa apartina clasei j este calculata printr-o metoda de superpozitie analoaga calculului potentialului electric produs într-un punct al spatiului de un numar de sarcini punctiforme. Rolul sarcinilor este preluat de vectorii prototip (esantioanele preclasificate) ai fiecarei clase. Functiile discriminant au forma:

, (9.29)

unde este functia potential. Proprietati dorite ale unei functii potantial sunt urmatoarele:

trebuie sa fie maxima pentru ,

0 la distanta mare de ,

sa fie o functie neteda, cu descrestere monotona în functie de distanta dintre vectorii argument,

Daca = , formele x₁ si x₂ ar trebui sa aiba aproximativ acelasi grad de similitudine cu .

Un exemplu de functie potential este

. (9.30)

Functiile potential pot avea forme diferite pentru clase diferite, ba chiar si pentru vectori de forma prototip diferiti. Puterea si generalitatea metodei este asigurata de faptul ca se garanteaza clasificarea corecta a tuturor esantioanelor de antrenament disponibile Meissel 1969

9.6. Tehnici de clasificare nesupervizata

Tehnicile de clasificare nesupervizata îsi propun sa descopere structurile ascunse într-un set de date, direct, fara asistenta unui "învatator" respectiv fara sa dispuna de esantioane preclasificate. Este firesc sa ne punem întrebarea când suntem într-o situatie atât de dificila încât sa nu dispunem de esantioane ale claselor. O problema de acest tip este chiar segmentarea imaginii, ce poate fi abordata ca o clasificare nesupervizata a pixelilor imaginii. Un alt motiv pentru a încerca o asemenea clasificare este legat de problema aproximarii distributiilor (uneori) complexe ale claselor ca un amestec de distributii simple. Tehnicile de clasificare nesupervizata urmaresc gruparea datelor în clase care contin date cu maxima asemanare. Din acest motiv, ele sunt adesea desemnate prin termenul de tehnici de grupare ("clustering"). În general, numarul de clase, K este considerat cunoscut. C nd nu este asa, se poate initia o procedura iterativa ce modifica numarul claselor pâna când se obtine o partitie a spatiului suficient de credibila. Credibilitatea poate fi evaluata, de exemplu, prin dispersiile claselor sau prin erorile maxime ale claselor. si în cazul clasificarii nesupervizate, sunt posibile cele doua tipuri de abordare: parametrica si neparametrica.

9.6.1. Clasificare nesupervizata parametrica folosind modelul gaussian

O distributie complexa poate fi aproximata eficient ca o însumare de distributii unimodale simple, între care distributia gaussiana reprezinta modelul cel mai frecvent adoptat. Considerând K clase, putem scrie:

,

unde parametrii sunt mediile si matricile de covarianta ale claselor:

(9.32)

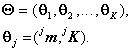
Problema ce trebuie rezolvata este estimarea parametrilor claselor, respectiv a mediilor si a matricilor de covarianta pentru maximizarea verosimilitatii:

. (9.33)

Din nou consemnam ca logaritmarea nu schimba relatia de ordine, fiind o operatie convenabila pentru simplificarea calculelor. O solutie eficienta, în doi pasi [Dempster 1977] o constituie algoritmul EM ("expectation maximization"). Notam cu M_jk.o variabila binara ce ia valoarea M_jk = 1 daca vectorul x_j a fost atribuit clasei k si M_jk = 0 în caz contrar. Algoritmul itereaza urmatorii doi pasi:

Pasul E "expectation") actualizeaza atribuirile la clase asteptate:

(9.34)

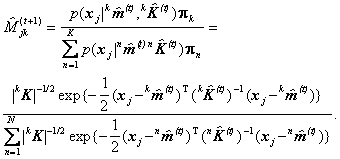
Pasul M ("maximization ) actualizeaza parametrii distributiilor componente:

(9.35)

. (9.36)

9.6.2. Clasificare nesupervizata neparametrica

Din aceasta categorie fac parte tehnicile de tipul cuantizarii vectoriale, bazate pe principiul partitionarii optimale a unei multimi de puncte în spatiul P dimensional. Unul dintre cei mai cunoscuti algoritmii de grupare din aceasta categorie [MacQueen 1967] este algoritmul mediilor ("K-means ). Functia obiectiv ce trebuie minimizata este eroarea patratica de aproximare a multimii vectorilor de intrare cu ajutorul unui numar K de vectori prototip:

, (9.37)

unde M_jk are semnificatia de la paragraful precedent. Prin derivarea ecuatiei de mai sus, se deduce imediat ca vectorii prototip ai claselor pentru o partitie, M_jk, data trebuie sa fie mediile celor K clase.

. (9.38)

Problema ce ramâne de rezolvat este determinarea partitiei optime, M_jk, cu j = 1,2,...,N si k = 1,2,...,K . Având în vedere ca dimensiunea spatiului solutiilor, 2 ^{N K} , exclude de regula cautarea exhaustiva, elaborarea unui algoritm eficient s-a dovedit necesara. Algoritmul se deruleaza în urmatoarea secventa de pasi:

Pasul 1. Initializeaza numarul de clase la valoarea K.

Pasul 2. Initializeaza mediile claselor, ^km, alegând (la întâmplare) primii K vectori. De exemplu,

^km = x_k , k = 1,2,..., K.

Pasul 3 Atribuie un vector nou, x_t+1, t > K, clasei cu media cea mai apropiata:

. (9.39)

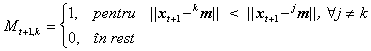
Recalculeaza media clasei înfunctie de noul membru:

. (9.40)

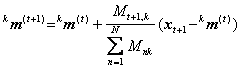
Pasul 4. Reia operatiile de la Pasul 3 cu mediile curente, incluzând acum si primii K vectori. Repeta (optional) acest pas pâna la convergenta.

Datorita simplitatii, algoritmul mediilor are numeroase limite. Rezultatul final depinde de numarul de clase dar si de mediile cu care se initializeaza algoritmul. Algoritmul mediilor face parte din categoria "algoritmilor lacomi" pentru ca încearca sa-si maximizeze functia obiectiv la fiecare pas, mergînd numai în directia de gradient maxim. Din acest motiv, gasirea minimului global al functiei obiectiv nu poate fi garantata. În general, functia obiectiv prezinta numeroase minime locale în care algoritmul poate esua. Totusi, algoritmul mediilor poate fi folosit cu succes în cazul datelor ce se grupeaza strîns în jurul unor medii separate de distante mari în raport cu dispersiile claselor. O versiune mai elaborata a algoritmului mediilor, capabila sa decida si asupra numarului de clase existent în datele analizate, este algoritmul ISODATA [Kaufman 1990] [Dumitrescu 1996]. Performantele algoritmilor de clasificare nesupervizata pot fi îmbunatatite folosind tehnici de optimizare. Unele implementari ale acestor tehnici se bazeaza pe retele neuronale.

9.7. Retele neuronale

Proprietatile statistice ale claselor sunt adesea necunoscute sau dificil de estimat. Din acest motiv, metodele de clasificare neparametrice, ce încearca optimizarea clasificatorului direct, pe baza informatiei statistice continute de esantioanele disponibile pentru instruire, s-au bucurat de o atentie deosebita. Între acestea, retelele neuronale au înregistrat în ultimul timp progrese importante. Preocuparile în domeniu sunt totusi mai vechi O retea neuronala este formata prin interconectarea unei multimi de elemente de prelucrare denumite neuroni. Modelul propus de McCulloch [McCulloch 1943] este inspirat din biologie, bazele matematice ale învatarii fiind elaborate de Hebb cu câtiva ani mai târziu Hebb 1949]. Dupa o perioada de optimism exagerat, temperat de articolul critic al lui Minsky si Papert [Minsky 1969], a urmat o relativa scadere a interesului în domeniu, considerat relansat în 1986 de cartea lui Rumelhart si McClelland [Rumelhart 1986]. Obiectivul acestui paragraf se rezuma la o scurta introducere a principiilor de baza ale retelelor neuronale si a câtorva din rezultatele curente cu impact mai important în prelucrarea imaginilor. Pentru o documentare comprehensiva, cititorul interesat poate consulta [Haykin 1994] sau [Dumitrescu 1996].

x xP

f(v)

v

y

w wP wP

q

Fig. 9.8. Modelul perceptronului

9.7.1. Modelul perceptronului

Perceptronul cu un singur strat (Fig. 9.8) este cea mai simpla retea neuronala, pe baza careia s-au dezvoltat toate celelalte retele neuronale utilizate în prezent. În contextul clasificarii formelor, perceptronul implementeaza o functie discriminant liniara, de forma:

, (9.41)

ce poate fi folosita cu succes pentru clasificarea formelor apartinând la doua clase liniar separabile. Coeficientii w_j, denumiti ponderi, modifica intrarile înainte de însumare, asemanator coeficientilor unui filtru într-o operatie de convolutie. Ecuatia

(9.42)

determina un hiperplan. Pentru a gasi o interpretare intuitiva a unor rezultate ulterioare, este util sa ne reamintim câteva rezultate din geometrie, în contextul unui spatiu multidimensional. Ecuatia (9.42) se poate scrie concis în forma:

, (9.43)

unde

= (w₁, w₂,...,w_P). (9.44)

Daca w_P , planul trece prin origine. Ca termen liber al ecuatiei (9.43), ponderea w_P , are un rol de prag si se noteaza adesea cu q, pentru a se evidentia acest lucru. Pentru ca este ortogonal cu orice vector din plan, vectorul are directia normalei la plan. Totodata, observam ca vectorul porneste prin origine. Un plan ce trece prin punctul definit de vectorul de pozitie x si are normala pe directia vectorului are ecuatia:

, (9.45)

care se mai poate scrie si în forma:

. (9.46)

Daca termenul al doilea al ecuatiei de mai sus reprezinta proiectia vectorului de pozitie x pe directia normala la plan. Deducem ca ^T x si similar |w_P+1 || reprezinta distanta minima de la un punct din plan la origine, adica distanta de la originea sistemului la planul de terminat de ecuatia (9.46), respectiv (9.43). Este convenabil sa definim un vector de clasa extins,

x = (x₁, x₂,..., x_P, 1)^T (9.47)

si un vector al ponderilor extins:

w = (w₁, w₂,..., w_P, w_P+1)^T. (9.48)

Pentru simplitatea notatiilor, nu am schimbat denumirea vectorului x, urmând sa facem precizarile necesare daca nu rezulta din context care varianta (extinsa sau normala) se foloseste. În spatiul extins, ecuatia (9.42) devine:

d(x) = w^T x = 0. (9.49)

Planul de decizie în spatiul extins trece prin origine. În plus, w contine toate ponderile si poate fi reprezentat în acelasi spatiu cu vectorul de forma extins. si în acest caz, vectorul ponderilor este normala la plan ce trece prin origine. Punctul ale carui coordonate sunt definite de w se afla pe acea parte a planului pentru care d(x) = w^T x > 0, pentru ca w^T w w > 0.

Pentru problema de clasificare cu doua clase, nu este nevoie de doua functii discriminant d (x) si d₂(x) pentru a separa clasele. Frontiera dintre cele doua clase ar avea ecuatia:

d (x) = d₁(x) d₂(x) = (w₁ w )^T x = 0,

care este de aceeasi forma cu (9.49). În consecinta, putem folosi o singura functie discriminant, de forma (9.49), pentru a decide ca x w daca w^T x > 0 si x w daca w^T x < 0

Iesirea, y, se obtine aplicînd suma obtinuta unei functii neliniare, denumite functie de activare. În exemplul de fata, functia de activare este un discriminator cu pragul 0:

. (9.50)

Mai concis,

. (9.51)

Prin urmare, c nd d(x) = w^T x > 0 si forma x este atribuita clasei w , y = 1, respectiv când w^T x < 0 si forma este atribuita clasei w , y = 1. Fie esantioanele de instruire ale clasei w si esantioanele de instruire ale clasei w . Clasele w si w sunt denumite liniar separabile, daca exista un vector al ponderilor, w, care clasifica fara eroare toate esantioanele disponibile.

9.7.2. Instruirea perceptronului

Procesul de instruire urmareste gasirea vectorului ponderilor, w, care clasifica exact toate esantioanele disponibile. Pentru determinarea algoritmului, este necesar sa definim o functie obiectiv pe care algoritmul o minimizeaza. Fie aceasta functie suma erorilor. Definim eroarea de clasificare a unei forme prin distanta ei la hiperplanul separator. Când x w si d(x) = w^T x > 0, eroarea este nula, în caz contrar eroarea este d(x). Similar, când x w si d(x) = w^T x < 0, eroarea este nula, în caz contrar eroarea este d(x). Pentru a nu avea semne diferite ale expresiei erorii la cele doua clase, este preferabil sa inversam semnul fiecarui vector de antrenament din clasa w . În acest mod, pentru orice vector x clasificat corect, d(x) = w^T x > 0 si daca d(x) < 0, eroarea este d(x). Presupunem ca w este initializat arbitrar, de exemplu w = 0. Notam w(k) vectorul ponderilor la pasul k si E(k) multimea vectorilor de forma clasificati eronat cu ajutorul vectorului w(k). Eroarea de clasificare totala este

J(k) = .

Algoritmul de instruire al perceptronului modifica la fiecare pas ponderile w, astfel încât eroarea sa se reduca în conformitate cu ecuatia

w(k + 1) = w(k) + a(k) , (9.53)

unde

. (9.54)

Parametrul a(k) este denumit rata de învatare sau de instruire si este un factor de proportionalitate, dependent în general de pasul de instruire, k. Acesta stabileste cât de mult se deplaseaza vectorul ponderilor pe directia gradientului erorii, în sensul invers, al scaderii acesteia. O valoare mare face ca algoritmul sa convearga mai rapid, cu riscul unei comportari instabile. În practica, 0 < a(k) < 1 si a(k) scade monoton cu numarul iteratiei, k. La implementarea algoritmului, se prefera ca la fiecare pas sa se foloseasca un singur esantion din setul de instruire. Regula de ajustare devine:

, (9.54)

unde x(k) sunt esantioane din lotul de instruire, normalizate de semn. Daca se folosesc esantioane nenormalizate de semn, regula de corectie se poate rescrie compact în forma:

, (9.55)

unde d_k este iesirea dorita (1 pentru x(k) w si 1 pentru x(k) w ) si y_k este iesirea reala. Factorul 1/2 este neesential, fiind inclus pentru consistenta cu ecuatia precedenta.

Dupa folosirea tuturor esantioanelor de antrenament, daca au existat esantioane clasificate incorect, procesul de ajustare a ponderilor se continua, folosind din nou esantioanele disponibile, pâna când vectorul w(k) nu se mai modifica pentru un numar de pasi egali cu numarul esantioanelor lotului de instruire sau s-a depasit un numar de iteratii limita. La fiecare reluare a unui ciclu de instruire, esantioanele se reordoneaza aleator.

Din ecuatiile (9.54) si (9.55), observam ca, prin regula de corectie, fiecare esantion clasificat incorect, x, tinde sa reorienteze hiperplanul de separatie astfel ca normala la plan, w(k) sa indice în directia punctului x. Daca esantionul este prezentat de un numar de ori suficient de mare, normala tinde sa devina paralela cu vectorul x, ceea ce asigura clasificarea corecta a formei x. Observatia sugereaza varianta de instruire alternativa, prin care fiecare esantion este prezentat perceptronului în mod repetat, pâna când este corect clasificat, apoi se continua cu alt esantion, pâna la epuizarea lotului de instruire. Prin teorema convergentei perceptronului [Haykin 1994], se demonstreaza ca algoritmul converge întotdeauna spre solutia ce asigura clasificarea corecta a tuturor esantioanelor, cu conditia ca clasele sa fie liniar separabile. Pentru probleme cu mai multe clase liniar separabile, se pot folosi mai multe unitati de tip perceptron, câte una pentru fiecare clasa. În cazul claselor ce nu sunt liniar separabile însa, algoritmul nu se stabilizeaza niciodata. 

9.7.3. Limitari ale preceptronului

În numeroase aplicatii de clasificare, intervin clase ce nu sunt liniar separabile. Perceptronul poate fi facut sa convearga spre o solutie stabila si în asemenea situatii, cu ajutorul algoritmului de instruire cunoscut sub denumirile Widrow-Hoff sau regula delta LMS ( de la "least mean square"). Impunând minimizarea erorii patratice:

J(w) = (1/2)(d w^Tx )², (9.54)

unde d_k este raspunsul dorit pentru esantionul x(k) si folosind acelasi algoritm de ajustare, bazat pe gradientul erorii, se gaseste [Haykin 1994] urmatoarea regula de ajustare a ponderilor:

. (

Pretul platit este ca nu se mai garanteaza separarea perfecta a claselor liniar separabile. Totusi vom arata ca limitarea principala a perceptronului nu provine din algoritmul de optimizare ci ea este datorata arhitecturii extrem de simple a retelei, cu un singur strat.

Unul din aspectele care au provocat cele mai mari dezamagiri în perioada de pionierat a studiului perceptronului a fost incapacitatea unei asemenea retele de a implementa o functie logica de tipul SAU EXCLUSIV (XOR). Sa presupunem ca avem o retea cu doua intrari booleene si raspunsul dorit al retelei este functia logica XOR, definita prin tabelul de adevar:

Tabelul 9.1.

În spatiul bidimensional (neextins) al formelor, esantioanele claselor sunt distribuite ca în Fig. 9.9.

x

w

w

w

d

d

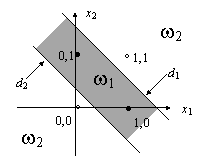
Fig. 9.9. Problema implementarii functiei SAU EXCLUSIV

Apare evident faptul ca pentru separarea claselor este nevoie de doua drepte, ceea ce nu se poate realiza cu un perceptron cu un singur strat, ce implementeaza o singura dreapta. Pentru a obtine doua drepte, este nevoie de doua structuri de tip perceptron, ceea ce ne apropie de solutie, dar nu este înca suficient. Raspunsurile celor doi perceptroni mai trebuiesc combinate pentru a se genera o iesire pozitiva pentru esantioane plasate între cele doua drepte si negativa în caz contrar. O structura posibila este redata în Fig. 9.10. Toti neuronii au functiile de activare de forma standard:

. (9.56)

Aceasta optiune este dictata de necesitatea de a asigura si la intrarea neuronului 3 variabile booleene. Datorita pragului ridicat, w₁₃= 3/2, primul neuron implementeaza o functie de tipul sI logic. Iesirea lui este la nivelul ridicat, 1 logic, numai daca ambele intrari, x₁, x₂, sunt în starea

S

x

x

S

S

f(v)

f(v)

f(v)

neuron

neuron

neuron 3

w

w

w

w

w

w

w

w

w

Fig. 9.10. Realizare posibila a functiei SAU EXCLUSIV cu o retea neuronala cu doua straturi

logica 1. Dreapta de decizie corespunzatoare, d , reprezentata în Fig. 9.9, are ecuatia:

. (9.57)

Neuronul 2 defineste dreapta de decizie d₂, paralela cu d₁ în Fig. 9.9 si are ecuatia:

. (9.58)

Se observa ca acest neuron implementeaza functia SAU logic între intrari, iesirea lui fiind la nivelul logic daca cel putin una din intrarile x₁, x₂ este în starea logica 1. Cititorul poate generaliza usor modalitatea de realizare a functiilor logice sI si SAU pentru un numar de intrari, n, arbitrar, prin alegerea adecvata a pragurilor, w_n+1 = n t si respectiv t, cu 0 < t < 1 si pastrarea tuturor ponderilor de indice mai mic la valoarea 1.

Neuronul al treilea este plasat în al doilea strat al structurii din Fig. 9.10. Rolul lui este de a realiza o combinatie liniara a iesirilor neuronilor din primul strat, pentru a genera regiunea de decizie dorita. Dreapta de decizie implementata are ecuatia:

. (9.59)

Iesirea neuronului 3 este pe zero logic când neuronul 1 este pe 1 logic, indiferent de starea neuronului 2. De asemenea, iesirea neuronului 3 este pe 0 logic daca neuronul 2 are iesirea 0 logic, independent de starea neuronului 1. Starea 1 logic la iesirea neuronului 3 si a retelei din Fig. 9.10 se obtine numai cînd neuronul 1 are iesirea 0 si neuronul 2 are iesirea pe starea 1. În ansamblu, reteaua din Fig. 9.10, decide pentru clasa w numai daca variabilele de intrare, x , x₂, sunt situate în regiunea umbrita din Fig. 9.9, încadrata de dreptele de decizie d si d₂. Folosind mai multi neuroni în primul strat, se obtin mai multe drepte, cu ajutorul carora se pot delimita în principiu regiuni convexe de complexitate arbitrara, recunoscute de neuronul din stratul al doilea. Numarul de neuroni trebuie sa fie suficient de mare pentru a face posibila definirea unor regiuni de decizie suficient de complexe. În acelasi timp, acest numar trebuie mentinut în limite rezonabile, pentru ca procesul de învatare prin care ponderile retelei se aduc la valorile corecte, necesare clasificarii, devine din ce în ce mai lent cu cresterea lui.

Pentru delimitarea unor regiuni neconvexe sau a unor regiuni formate din reunuinea mai multor regiuni convexe, conexe sau nu, este necesara adaugarea unui al treilea strat la reteaua neuronala. Se poate arata ca un numar de trei straturi este suficient pentru generarea unor regiuni de decizie de forma oricât de complicata. Este motivul pentru care retelele neuronale cu trei straturi se bucura de o utilizare foarte larga.

9.7.4. Perceptronul multistrat

Structura din Fig. 9.10 poate fi generalizata pentru a se obtine o arhitectura cu mai multe straturi. Primul strat al retelei din figura este format din numai neuronii 1 si 2. Ei sunt denumiti neuroni ascunsi, pentru ca iesirile lor sunt inaccesibile în exteriorul retelei. În mod curent, primul strat contine un numar de neuroni mult mai mare, de ordinul zecilor sau chiar mai mare, dependent de dimensiunea spatiului formelor. Adaugând un nou strat ascuns, care contine în general un numar de neuroni mai mic decât stratul de intrare si completând stratul de ietire cu numarul de neuroni necesar, egal cu numarul claselor ce trebuiesc identificate, se obtine o retea cu trei straturi. Fiecare neuron al unui strat este interconectat cu toti neuronii din stratul urmator. Pentru a putea antrena eficient o asemenea retea, mai este necesara o modificare aparent minora, dar importanta fata de structura din Fig. 9.10. Functia de activare trebuie sa devina continua, derivabila si monoton crescatoare, astfel încât, pentru toate valorile iesirii y = f(v), derivata sa fie diferita de zero. O asemenea functie, denumita sigmoida, are un grafic de forma prezentata în Fig. 9.11 si expresia:

.

v

q

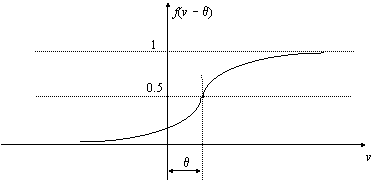
Fig. 9.11. Functie de activare sigmoida

Parametrul a controleaza aliura, mai abrupta sau mai neteda a functiei. Panta functiei:

(9.61)

este maxima în origine si are valoarea a 0.5 = a/4. Experienta practica arata ca viteza de învatare este mai buna daca functia este simetrica (simetrie impara) fata de origine. De exemplu, se poate folosi functia:

. (9.62)

Se observa ca în esenta avem de-a face cu aceeasi functie, rescalata si decalata cu o constanta, pentru a se anula în origine. Valori recomandate [Haykin 1994] pentru constantele a si b sunt a si b

Algoritmul de instruire poate fi dedus (vezi de exemplu [Haykin 1994]) printr-o procedura denumita cu propagarea erorii înapoi, care consta în urmatoarele etape:

se aplica un esantion din lotul de instruire la intrarea retelei

se propaga înainte intrarea retelei pentru a se obtine iesirile fiecarui neuron

se compara iesirile neuronilor din stratul de iesire cu raspunsurile dorite

se calculeaza o masura a erorii în stratul de iesire

se modifica ponderile conexiunilor spre stratul de iesire pentru a reduce eroarea

cunoscând efectul iesirilor stratului penultim asupra erorii în stratul de iesire, se determina modificarile necesare ale ponderilor la intrarea stratului penultim, pentru reducerea erorii în stratul de iesire

se continua procedura prin modificarea ponderilor fiecarui strat, de la iesire spre intrare, pâna se ajunge la ponderile neuronilor din primul strat

se continua procedura folosind toate esantioanele lotului de antrenament si reluând acest ciclu cu esantioanele prezentate în ordine diferita, pâna când eroarea se stabilizeaza la o limita acceptata

Fiecare pas al optimizarii ponderilor se bazeaza, ca si în cazul algoritmului Widrow-Hoff, pe gradientul instantaneu al erorii. În final, se ajunge la algoritmul redat în continuare în sinteza.

Se noteaza:

w^(l) = vectorul ponderilor pentru un neuron din stratul l,

q^(l) = pragul unui neuron din stratul l,

v^(l) = vectorul activitatilor neuronilor din stratul l,

y^(l) = vectorul semnalelor de iesire ale neuronilor din stratul l,

d^(l) = vectorul gradientilor locali ai neuronilor din stratul l,

e = vectorul eroare la iesirea retelei.

N_l = numarul neuronilor stratului l

Lotul de instruire consta în multimea , unde x(n) sunt vectori de instruire si d(n) raspunsurile dorite pentru vectorii de instruire. Pentru stratul de intrare, l = 0. Ponderea conexiunii dintre neuronul i din stratul l si neuronul j din stratul l 1 se noteaza . Se considera un numar de L straturi.

Pasul 1. Initializare. Se initializeaza ponderile si pragurile folosind numere aleatoare mici, cu distributie uniforma. Initializeaza constantele de învatare, a si h (valori recomandate a h = 0.1).

Pasul 2. Prezentarea esantioanelor de instruire la intrarea retelei, într-o ordine oarecare. Pentru fiecare esantion, îndeplineste secventa de calcule înainte si înapoi, descrise la pasii 3 si 4.

Pasul 3. Calculul direct.

3.1. Se porneste cu l = 1si se determina activarea fiecarui neuron prin ecuatia:

.

Pentru primul strat, 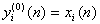si N₀ = P, dimensiunea vectorului de intrare, x. Totodata, si .

3.2. Se determina iesirile neuronilor:

.

Iesirile ultimului strat se noteaza:

.

3.3. Se determina semnalul de eroare:

.

Pasul 4. Calculul invers.

4.1. Se determina succesiv gradientii locali ai retelei, începând cu stratul de iesire si continuând strat cu strat, spre intrare:

pentru neuronul j al stratului de iesire, L si

pentru neuronul j al stratului ascuns l.

4.2. Modifica ponderile retelei în stratul l, conform regulii delta generalizate:

.

Pasul 5. Iteratii. Dupa folosirea întregului lot de instruire, reia procedura descrisa mai sus, cu esantioanele prezentate într-o alta ordine, stabilita aleator, pâna la stabilizarea ponderilor si atingerea performantelor de eroare medie pe întregul lot dorite.

Observatii

Proiectarea unei retele cu propagare înapoi pune numeroase probleme, nu toate solutionate teoretic satisfacator pâna în prezent. Între acestea, mentionam:

alegerea numarului optim de neuroni ai straturilor intermediare ascunse

alegerea parametrilor de învatare, a si h (inclusiv modificarea lor adaptiva pe parcursul instruirii)

initializarea ponderilor, pentru evitarea saturarii premature a iesirilor si agatarea retelei în minime locale

Cu toate acestea, performantele de clasificare raportate în numeroase aplicatii sunt foarte bune si asimptotic echivalente celor obtenabile cu clasificatorul optimal Bayes.

9.7.5. Retele neuronale cu auto-organizare

Retelele neuronale cu auto-organizare sunt destinate învatarii nesupervizate, fiind capabile sa descopere singure structurile continute de datele prezentate. Exista o asemanare pronuntata cu algoritmii de grupare si în particular cu algoritmul mediilor. De regula, aceste retele contin un singur strat de neuroni. Neuronii folositi sunt liniari, în sensul ca nu au functii de activare neliniare. Se poate considera ca f(v) = v. În consecinta, neuronul este caracterizat prin relatia liniara simpla:

y = w^Tx. (9.63)

Algoritmul Hebbian generalizat

Ideea de baza a algoritmilor hebbieni este de a întari ponderile pentru intrarile neuronului ce sunt în corelatie cu iesirea. O regula hebiana simpla pentru actualizarea ponderilor este:

w(n +1) = w(n) + ay(n)x(n), (9.64)

cu parametrul a reprezentând rata de învatare. Regula este însa instabila, existând tendinta ca iesirea sa creasca nelimitat. Stabilitatea se poate obtine usor, prin adaugarea operatiei de normalizare a ponderii:

. (9.65)

S-a demonstrat [Oja 1985] ca aceasta regula converge spre componenta principala cea mai mare a intrarii (componenta corespunzatoare valorii proprii celei mai mari n analiza Karhunen-Loeve). Folosind o dezvoltare în serie a expresiei de mai sus, Oja a liniarizat regula de instruire, în forma:

w(n +1) = w(n) + a y(n)x(n) y²(n)w(n)].  (9.66)

Pentru extragerea unui numar de k componente principale, reteaua se construieste cu un numar de neuroni oarecare si se foloseste regula de instruire hebbiana generalizata:

w_j(n +1) = w_j(n) + a(n)y_j(n) x(n) ], (9.67)

unde este re-estimatorul, definit prin

. (9.68)

Se observa ca re-estimatorul forteaza iesirile sa învete componente principale diferite, scazând estimate ale componentelor deja gasite înainte de a implica datele în procesul de învatare. Daca numarul esantioanelor prezentate este mare, ponderea w_ji a neuronului j converge spre componenta cu indicele i a vectorului propriu asociat cu a j-a valoare proprie a matricii de autocorelatie a vectorilor de intrare, x(n).

Algoritmul Kohonen

Algoritmul Kohonen [Kohonen 1982] presupune, de asemenea, o arhitectura de retea simpla, compusa din neuroni liniari, organizati într-un singur strat. Spre deosebire de retelele discutate pâna acum, între neuronii unei retele Kohonen se stabilesc conexiuni laterale, asemenea celor existente în sistemul vizual uman. Interconexiunile unui neuron se limiteaza la o anumita vecinatate a sa. Ca rezultat al acestor conexiuni, neuronii vecini tind sa dobândeasca prin instruire ponderi sinaptice similare. Dupa procesul de instruire, vectorii pondere ai retelei tind sa se grupeze în functie de distributia statistica a esantioanelor de intrare, aglomerându-se mai mult în regiunile cu densitate de probabilitate mai mare.

Pentru fiecare neuron, w_j, se defineste o vecinatate, V_j. În acest scop, uzual neuronii sunt organizati si indexati unidimensiunal (liniar sau circular [Neagoe 19XX]) sau bidimensional, conform exemplelor din Fig. 9.12. Pe parcursul procesului de instruire, dimensiunile vecinatatii fiecarui neuron se modifica, fiind maxima la început si reducându-se treptat, conform unei anumite strategii. Algoritmul Kohonen face parte din categoria metodelor de instruire competitive, fiind înrudit cu algoritmul de grupare al mediilor, pe care îl generalizeaza. Îl prezentam în continuare:

Pasul 1. Initializare. Se stabileste numarul de clase (neuroni) P. Se defineste o masura a distantei (uzual norma euclidiana). Se stabileste un criteriu de eroare pentru oprire, e > 0. Se initializeaza variabila timp, n si rata de învatare, a n (0,1) si marimea vecinatatii V_j(n). Uzual aceasta contine initial toti neuronii sau jumatate din numarul total, P. Pentru asigurarea unei convergente bune, rata de învatare are initial o valoare apropiata de 1 si se va reduce treptat, pe parcursul procesului de instruire. Se atribuie la întâmplare valori mici ponderilor w_j(n). Singura restrictie este sa nu existe doua ponderi initiale identice.

wj

wij

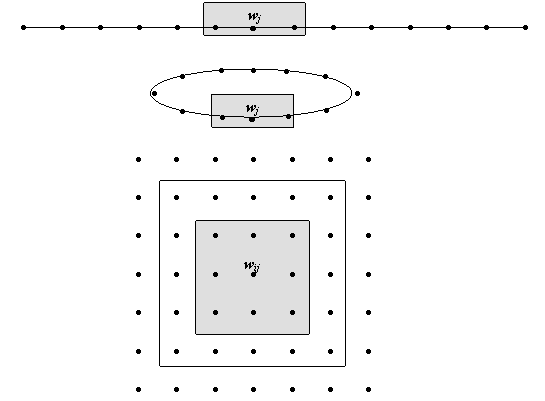
Fig. 9.12. Diferite tipuri de vecinatati pentru o retea Kohonen

Pasul 2. Esantionare. Se extrage un vector x(n) din lotul de instruire.

Pasul 3. Testul de similitudine. Se cauta neuronul cel mai apropiat (câstigatorul):

i(n) = arg min _j , j = 1,2,...,P. (9.69)

Pasul 4. Actualizare ponderi. Ajusteaza vectorii ponderilor pentru toti neuronii din vecinatatea neuronului câstigator:

(9.70)

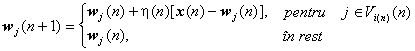
Efectul ajustarii este de a atrage vectorul ponderilor spre esantionul nou, proportional cu rata de învatare.

Pasul 5. Continuare. Continua de la Pasul 2, pâna când

||w_j(n+1) w_j(n)|| < e

pentru întreg lotul de instruire (pentru P pasi consecutivi).

Strategia de modificare a ratei de învatare si a vecinatatii joaca un rol important în succesul operatiei de instruire. Din pacate, baza teoretica pentru alagerea acestor parametri este inexistenta deocamdata, experienta având un rol determinant. Conform recomandarilor lui Kohonen [Kohonen 1990a], rata de învatare trebuie mentinuta constanta si apropiata de valoarea 1 pe parcursul primelor aproximativ 1000 de iteratii. Apoi trebuie sa scada treptat, ramânând mai mare decât 0.1, pentru un numar de iteratii necesare organizarii vectorilor pondere. Legea de modificare a ratei nu este critica. În faza finala si relativ lunga, de convergenta, destinata ajustarii fine a pozitiilor vectorilor pondere, h n) va avea o valoare de ordinul 0.01 sau chiar mai mica. Faza de convergenta necesita un numar de iteratii de ordinul miilor. O alta varianta posibila de modificare a ratei de învatare este:

(9.71)

Fata de varianta de baza a algoritmului, sunt posibile modificari, menite sa conduca la performante superioare.

Reformularea vecinatatii

Algoritmul de baza ajusteaza la fel toti neuronii din vecinatatea neuronului câstigator, fapt aflat în discordanta cu functionarea sistemelor neurale biologice. S-a aratat anterior, ca în cazul sistemului vizual uman, conexiunile laterale scad în intensitate cu distanta, dupa o functie modelata bine de derivata a doua a unei gaussiene. Regula de instruire poate fi modificata pentru a corecta rata de învatare cu un factor dependent de distanta pâna la neuronul câstigator:

, (9.72)

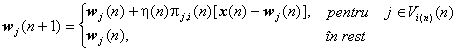
unde

. (9.73)

Variatia temporala a dispersiei în exponentiala de mai sus se poate alege a fi tot exponentiala,

, (9.74)

cu t o constanta de timp. O lege de variatie similara se poate folosi si pentru rata de învatare:

. (9.75)

Mecanismul constiintei

O modificare posibila a algoritmului Kohonen consta în includerea unui mecanism al constiintei, menit sa descurajeze câstigarea prea frecventa a competitiei de catre unii neuroni. Denumirea sugereaza ca un neuron care câstiga prea des trebuie sa se simta vinovat de acest lucru si în consecinta sa se abtina de la participare. Prin egalizarea numarului de câstiguri între neuronii retelei, se obtine o reprezentare mai fidela a distributiei statistice a esantioanelor lotului de instruire. Modificarea afecteaza testul de similaritate, prin introducerea unui handicap ce tine cont de fractiunea de timp de câstig a fiecarui neuron. Functia de similitudine se modifica în forma:

i(n) = arg min _j , j = 1,2,...,P. (9.76)

Functia handicap se defineste prin ecuatia:

, (9.77)

unde p_j(n) este fractiunea de timp de câstig si o constanta pozitiva cu valoarea tipica 10. Fractiunea de timp de câstig se actualizeaza recursiv prin formula:

p_j(n + 1) = (1 b) p_j(n) + by_j(n), (9.78)

unde y_j(n) este iesirea neuronului, egala cu 1 când este câstigator si 0 în rest. Constanta b se alage foarte mica, de ordinul 10 . Cu mecanismul constiintei inclus, algoritmul Kohonen se încadreaza în categoria metodelor de învatare competitiva senzitiva la frecventa ("frequency sensitive competitive learning" FSCL) ce au demonstrat proprietati interesante pentru compresia imaginilor prin tehnici de cuantizare vectoriala.

9.7.6. Structuri hibride

Retele neuronale hibride, ce combina învatarea supervizata cu cea nesupervizata, permit obtinerea unor performante de clasificare foarte bune, în conditiile unui proces de învatare mai rapid convergent [Kangas 1990], [Rogers 1991]. O schema-bloc posibila este redata în Fig. 9.13. În

ALGORITM KOHONEN

CLASIFICATOR LINIAR

Vectori intrare x

Învatator

Fig. 9.13. Clasificator cu structura hibrida

esenta, algoritmul Kohonen actioneaza ca un preprocesor ce transforma neliniar datele de intrare, facând posibila separarea lor cu un clasificator liniar. Acesta din urma este instruit de o maniera supervizata, de exemplu cu ajutorul algoritmului LMS (Widrow-Hopf). O alta structura hibrida cu performante de clasificare foarte bune se obtine prin asocierea retelei Kohonen cu clasificatorul LVQ. Schema bloc este similara cu schema din Fig. 9.13, locul clasificatorului liniar fiind luat de clasificatorul LVQ.

Clasificatorul LVQ

Initialele provin de la prescurtarea denumirii "learning vector quantization", cuantizor vectorial cu învatare. Neuronii cuantizorului vectorial determina o partitionare a spatiului formelor în celule elementare, denumite si celule Voronoi. Fiecarui vector pondere al retelei, îi corespunde o celula, formata din acele puncte ale spatiului de intrare care sunt mai apropiate de vectorul pondere respectiv decât de oricare alt vector. Definitia implica o metrica, uzual cea euclidiana si regula deatribuire a vecinului celui mai apropiat. Regula de învatare se aseamana cu cea folosita de algoritmul Kohonen, ceea ce poate sa nu surprinda, având în vedere faptul ca a fost propusa de acelasi autor [Kohonen 1990b]. Deosebirea principala se datoreaza folosirii informatiei referitoare la apartenenta la clasa a esantioanelor de antrenament. Fie w_c vectorul Voronoi cel mai apropiat de esantionul de intrare curent, x_i, prezentat la intrarea LVQ. Fie w_c si w_i clasele asociate vectorului Voronoi, respectiv vectorului de intrare. Vectorul Voronoi este ajustat dupa cum urmeaza:

Daca , w_c w_i atunci

w_c(n+1) = w_c(n) + a(n)[ x_i w_c(n)] (9.79)

În cazul contrar,

w_c(n+1) = w_c(n) a(n)[ x_i w_c(n)]. (9.80)

Ceilalti vectori Voronoi nu sunt modificati. Se observa ca vectorii de instruire clasificati corect de retea atrag vectorii Voronoi, în timp ce vectorii clasificati incorect îi resping. Din nou, a(n) este constanta de învatare, ce porneste de la o valoare cuprinsa între 0 si 1 si scade treptat pe parcursul instruirii, spre a asigura convergenta algoritmului. Algoritmul LVQ poate fi privit ca un algoritm de aproximare stohastica. Convergenta lui este foarte rapida. În combinatia cu reteaua de preprocesare Kohonen, vectorii Voronoi sunt initializati la valori apropiate de cele ideale, fazei de instruire revenindu-i doar rolul unor ajustari de finete.

Bibliografie

Cover T.M., The best two independent measurements are not the two best. IEEE Trans. on Syst., Man and Cybern., Vol. SMC-4, 1974, 116-117.

Dumitrescu D., Costin H., Retele neuronale. Teorie si aplicatii. Teora, 1996

Foley D.H., Considerations on sample and feature size. IEEE Trans. on Information Theory, Vol. IT-18, 1972, 618-626.

Hart, P.E., Condensed nearest neighbor rule. IEEE Trans. on Information Theory, Vol. IT-14, No. 3, 1968, 515-516.

Haykin S., Neural Networks. A Comprehensive Foundation. Prentice Hall, NJ, 1994.

Hebb D.O. The organization of Behavior:A Neuropsychological Theory. Wiley, New York, 1949.

Highleyman W.H., The design and analysis of pattern recognition experiments. Bell Sys. Tech. Journal 41, 1962, 723 T.

Kangas J., Kohoneh T., Laaksonen J., Variants of self-organizing feature maps. IEEE Trans. on Neural Networks 1, 1990, 93-99. 

Kaufman L, Rousseeuw P.J., Finding Groups in Data: An Introduction to Cluster Analysis John Wiley and Sons, New York, 1990.

Kohonen T., Self-organized formation of topologically correct feature maps. Biological Cybernetics 43, 1982, 59-69.

Kohonen T., The self-organizing map. Proceedings of the IEEE, 78, 1990, 1464-1480.

Kohonen T., Improved versions of vector quantization. International Joint Conference on Neural Networks, San Diego, CA, Vol. 1, 1990, 545-550.

MacQueen J, Some methods for classification and analysis of multivariate observations. Proceedings of the 5^th Berkeley Symposium on Mathemetical statistics and Probability, 1967, 281-297.

McCulloch, W.S., Pitts, W., A logical calculus of the ideas immanent in nervous activity, Bulletin of Mathematical Biophysics 5, 1943, 115-133.

Meisel W.S., Potential functions in mathematical pattern recognition. IEEE Trans. on Computers, Vol. C18, No. 10, 1969, 911-918.

Minsky M.L., Papert S.A., Perceptrons. MIT Press, Cambridge, MA, 1969.

Mucciardi A.N., Gose E.E., A comparison of seven techniques for choosing subsets of pattern recognition properties. IEEE Trans. on Computers, Vol. C-20, 1971, 1023-

Neagoe, V.E.,

Oja E., Karhunen J., On stochastic approximation of the eigenvectors and eigenvalues of the expectation of a random matrix. J. Math. Anal. and Appl. Vol. 106, 1985, 69-84.

Rogers S.K., Kabrisky M., An introduction to biological and artificial neural networks for pattern recognition. SPIE, Bellingham, Wa, 1991.